基于深度强化学习的车辆紧急制动策略

韩 玲，张 晖，方若愚，刘国鹏，朱长盛，殷朝霞, 迟瑞丰

(长春工业大学 机电工程学院， 吉林 长春 130012)

0 引 言

启发式算法自动紧急制动可在危险情况下主动采取制动措施，有效保护车辆驾驶员及其他交通参与者，是保证行车安全关键部分[1]。随着汽车智能化的发展，紧急制动作为不可或缺的环节，其重要程度更加得到凸显[2]。

近年来，自动紧急制动得到广泛关注与研究，目前自动紧急制动方法主要分为两类：基于建立安全时间或安全距离模型的方法和通过评估风险建立碰撞概率模型的方法。文献[3-4]提出基于安全距离-时间模型相结合的汽车紧急制动控制策略，基于安全时间模型设计了以相邻车辆、相邻车辆相对速度为输入，建立安全时间与安全距离相结合的模型，通过警报分级制动等方式确保行车安全。刘哲等[5]提出通过使用安全时间模型求解期望减速度，防止车辆碰撞。此类通过建立模型的方法在简单路况或单一场景下通常具有良好的效果，但在动态过程中通常难以建立准确的模型，且所建立模型很难适应变化的环境。

基于评估风险的紧急制动方法也得到广泛应用，Lee D等[6]提出通过先轻减速，随后预测碰撞概率决定减速力度的方式，有效避免了过度减速对自车及周围车辆可能造成的危险。孟柯等[7]通过风险预测对最危险目标碰撞态势进行实时判断，从而降低车辆与行人间的碰撞概率。基于风险模型的方法通过选择碰撞概率最小的动作避免发生碰撞，然而行车过程中的风险因素是动态变化的，难以利用风险模型完全描述。

随着算力的提升，以DQN为代表的深度强化学习方法展现了独特的优势，获得了广泛应用[8-9]，DQN通过其独特的动作-批评结构与环境交互训练，实现自主决策。不依赖于精确的数学模型，对解决复杂动态规划问题有良好的表现[10]。因此，为解决紧急制动问题，提高行车过程中的安全性，首先推导DQN算法，并依据紧急制动过程建立深度强化学习环境，随后构建基于DQN的紧急制动策略，所构建策略可通过与环境交互自主学习实现在危险情况下自主判断刹车幅度，并且不需要针对环境建立精确复杂模型。

1 深度强化学习算法

1.1 DQN与环境交互过程

DQN与环境交互过程如图1所示。

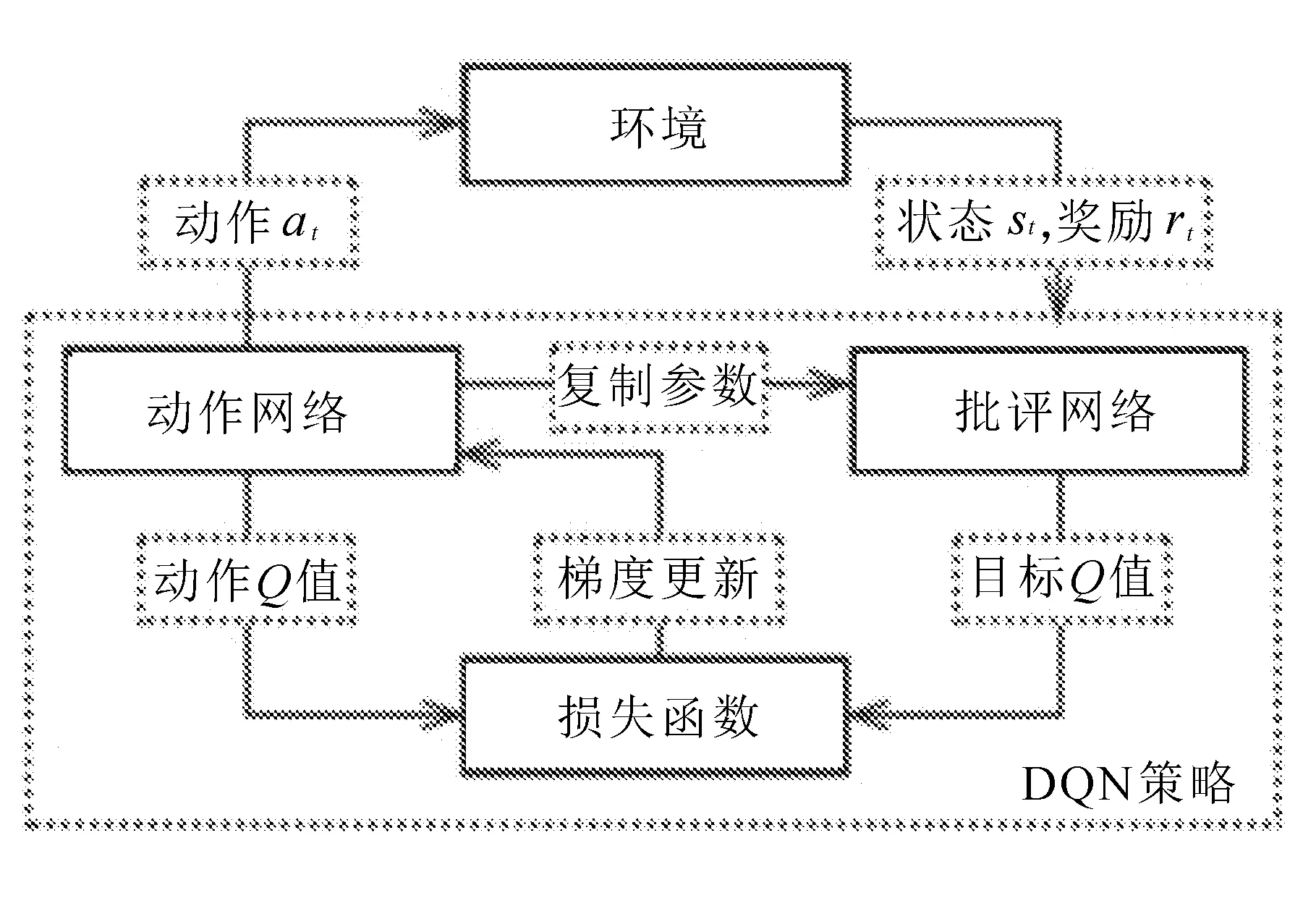
图1 DQN与环境交互过程

DQN通过与环境交互探索最优策略。其交互过程为：t时刻动作网络从环境中获取状态st，根据状态计算所有动作的Q值，并选择Q值最大的动作执行与环境交互，环境根据动作执行后产生的影响，返回奖励值rt，批评网络依据返回的奖励值重新计算动作的Q值，称为该动作的目标Q值，损失函数依据动作网络计算得到的Q值与批评网络计算得到的目标Q值的差距，对动作网络进行梯度更新，批评网络的更新依据每隔一段时间完全复制动作网络的参数进行更新。

1.2 DQN算法

Q值作为评价动作优劣的指标与环境返回的奖励值相关，因此，首先定义动作执行后的奖励为

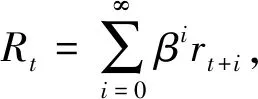
(1)

式中：Rt----t时刻动作执行后环境反馈的奖励，由当前时刻与未来时刻获得奖励构成;

rt+i----当i为0时，表示当前获得的奖励,i大于0时，表示未来时刻获得的奖励;

β----折扣系数，表示未来时刻对奖励的影响程度。

DQN策略可执行动作被预先定义好，则任一动作ax的Q值定义为

Q(st,ax)=E(Rt|s=st,a=ax)。

(2)

Q(st，ax)表示在状态st下动作ax的Q值，则式中表示动作的Q值为动作获得奖励的期望值。

明确动作的Q值后，进一步明确动作网络的输入与输出，动作网络作为神经网络只需要明确其输入输出即可，动作网络表达为

V动作(ω)=maxE(Q(st,a1),(st,a2),…,(st,an)),(3)

式中：ω----网络参数。

动作网络在t时刻状态st下，依据当前状态，估计所有动作的Q值，并选择Q值最大的动作为输出。将式(1)代入式(2)得

E(rt+maxβ(Q(st+1,a1),Q(st+1,a2),…,

Q(st+1,an))|s=st,a=ax)。(4)

t时刻动作的Q值可由t时刻立刻获得的即时奖励与下一时刻动作的Q值构成。

依据式(4)，批评网络提取动作执行后环境反馈的奖励与估计下一时刻最优动作的Q值，计算当前时刻动作的Q值，批评网络表示为

V批评(ω)=rt+βmaxE(Q(st+1,a1),Q(st+1,a2),

…,Q(st+1,an))，

(5)

式中：rt----动作执行后立即获得的奖励。

由于批评网络所依据即时奖励为动作执行后环境反馈，而动作网络估计的Q值是通过预估得到，因此批评网络计算得到的Q值被视为更接近真实值。

通过将动作网络估计得到动作的Q值与批评网络计算得到动作的Q值代入损失函数，根据损失函数计算结果对动作网络进行梯度更新，令动作网络估计得到的Q值不断逼近批评网络计算得到的Q值，使动作网络具备依据环境输入状态选择合适动作的能力，损失函数被定义为

L(ω)=maxE(Vcritic(ω)-Vactor(ω))2=

maxE[((rt+βmaxE(Q(st+1,a1),

Q(st+1,a2),…,Q(st+1,an)))-

(maxE(Q(st,a1),Q(st,a2),…,

Q(st,an))))2]。

(6)

DQN算法即通过动作网络选择合适的动作进行输出与环境交互，批评网络根据环境反馈重新计算动作的Q值，并通过在损失函数内对动作网络进行更新的方式，得到最优策略，与大多数策略依据建立精确复杂的模型不同，DQN只需建立用于交互的环境模型，适应动态复杂的交通环境，且具备自主学习探索策略的能力。

2 基于DQN算法的紧急制动策略

2.1 紧急制动过程环境建模

DQN算法通过与环境交互，自主探索最优策略，因此，首先建立紧急制动过程的环境模型，模型由两部分组成，车辆前方摄像头获取的图像以及当前车速。摄像头获取的图像如图2所示。

图2 摄像头获取图像

2.2 深度强化学习元素

为建立基于提出DQN算法的紧急制动策略模型，需定义深度强化学习与环境交互时的重要元素，分别为状态、动作和奖励。

2.2.1 状态

建立环境模型，模型由所有时刻车辆前方摄像头获取的图像以及当前车速构成。则DQN策略由环境输入状态，即为当前时刻车辆前方摄像头获得图像及当前时刻车速。

2.2.2 动作

DQN可执行的动作需要预先定义，因此定义刹车动作，刹车幅度为0至1.0，刹车幅度为0时，则不刹车，为1.0时表示刹车开度最大，因此定义6个动作，分别为刹车幅度0，0.2，0.4，0.6，0.8，1.0。

2.2.3 奖励函数

奖励函数用以反馈动作执行后的即时奖励，奖励函数定义为

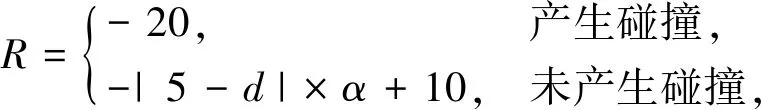
式中：α----奖励折扣系数，以确保未产生碰撞时奖励为正;

d----与前方车辆距离，则产生碰撞返回一个负奖励，而安全停止返回一个正奖励，且与前车距离越接近5 m，则获得奖励越大。

2.3 基于DQN的紧急制动策略模型

基于DQN的紧急制动策略如图3所示。

t时刻环境模型将当前车速与车前摄像头获取图像作为状态st输入动作网络，动作网络根据状态估计所有动作的Q值，并选择其中Q值最大的动作at执行，动作执行后环境返回即时奖励rt,并更新状态为st+1,将st,rt,at,st+1存入经验池中，批评网络依据st+1,rt重新计算动作Q值，并与动作网络估计的Q值一同输入损失函数，根据损失函数结果梯度更新动作网络，批评网络的更新则通过每隔一段时间完全复制动作网络的参数完成。

图3 基于DQN的紧急制动策略

3 仿真与结果分析

为验证所提出基于DQN的紧急制动策略的性能，在Carla仿真环境中进行仿真验证，如图4所示。

图4 Carla仿真环境

Carla为一款开源的无人驾驶仿真软件，可实时获取车辆速度及车辆前置摄像头图像等，在Carla仿真环境中，设置两个场景，对比基于DQN的紧急制动策略与基于专家决策的紧急制动性能。

仿真场景一如图5所示。

图5 仿真场景一

黑色车辆为实验车辆，白色车辆为其他车辆，黑色车辆实验中分别搭载训练后的基于DQN的紧急制动策略及基于专家决策的紧急制动策略，两车在实验过程中以不同速度行驶，初始距离为30 m，白车于行驶过程中急刹车，观察实验车辆的制动情况。

两车以不同速度行驶如图6所示。

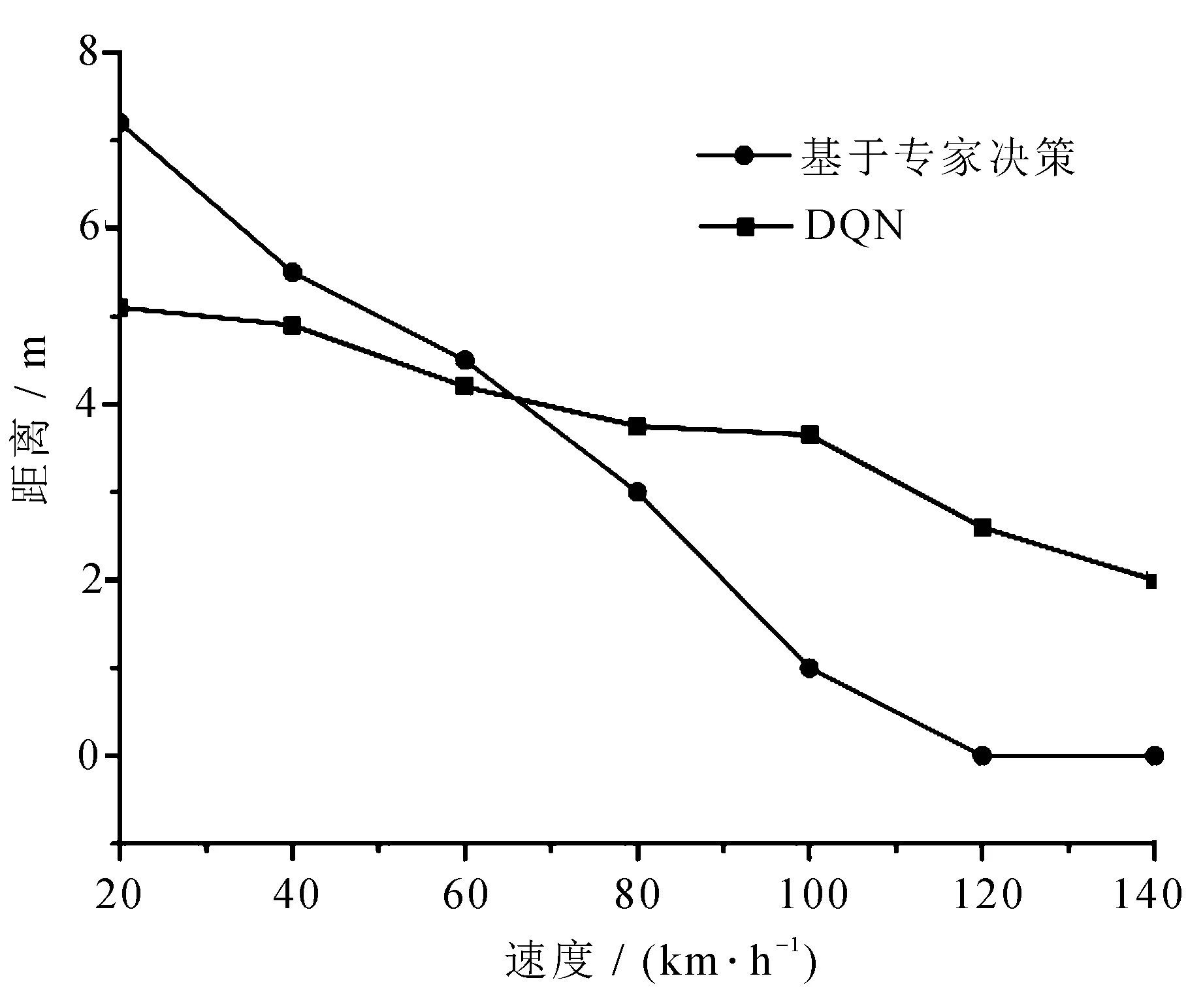
图6 不同速度实验车辆与前车相距距离

分别搭载基于DQN的紧急制动策略与搭载基于专家决策的制动策略下，前车急停后，实验车辆停止时与前车相距距离，速度较低时，基于专家决策的方法停止后距离前车大于基于DQN的紧急制动策略；而当速度较高时，基于专家决策的方法刹车距离小于基于DQN的紧急制动策略，且当速度大于120 km/h后，基于专家决策的方法与前车发生碰撞，而基于DQN的紧急制动策略始终保持不发生碰撞，且速度较低时，停止后与前车距离维持在5 m附近，而在速度较高时，其停止后距离也大于基于专家决策的方法，且始终未产生碰撞，所提出基于DQN的紧急制动策略具有更好的安全性。

仿真场景二如图7所示。

图7 仿真场景二

黑色车辆为实验车辆，白色车辆为其他车辆，实验车辆分别搭载基于DQN的紧急制动策略与基于专家决策的紧急制动策略，当距离路口不同距离时,白色车辆以150 km/h从路口驶出，并在道路中央停止，分别在不同距离下进行20次实验，记录两种方法发送碰撞的概率。

距离路口不同距离下发生碰撞概率如图8所示。

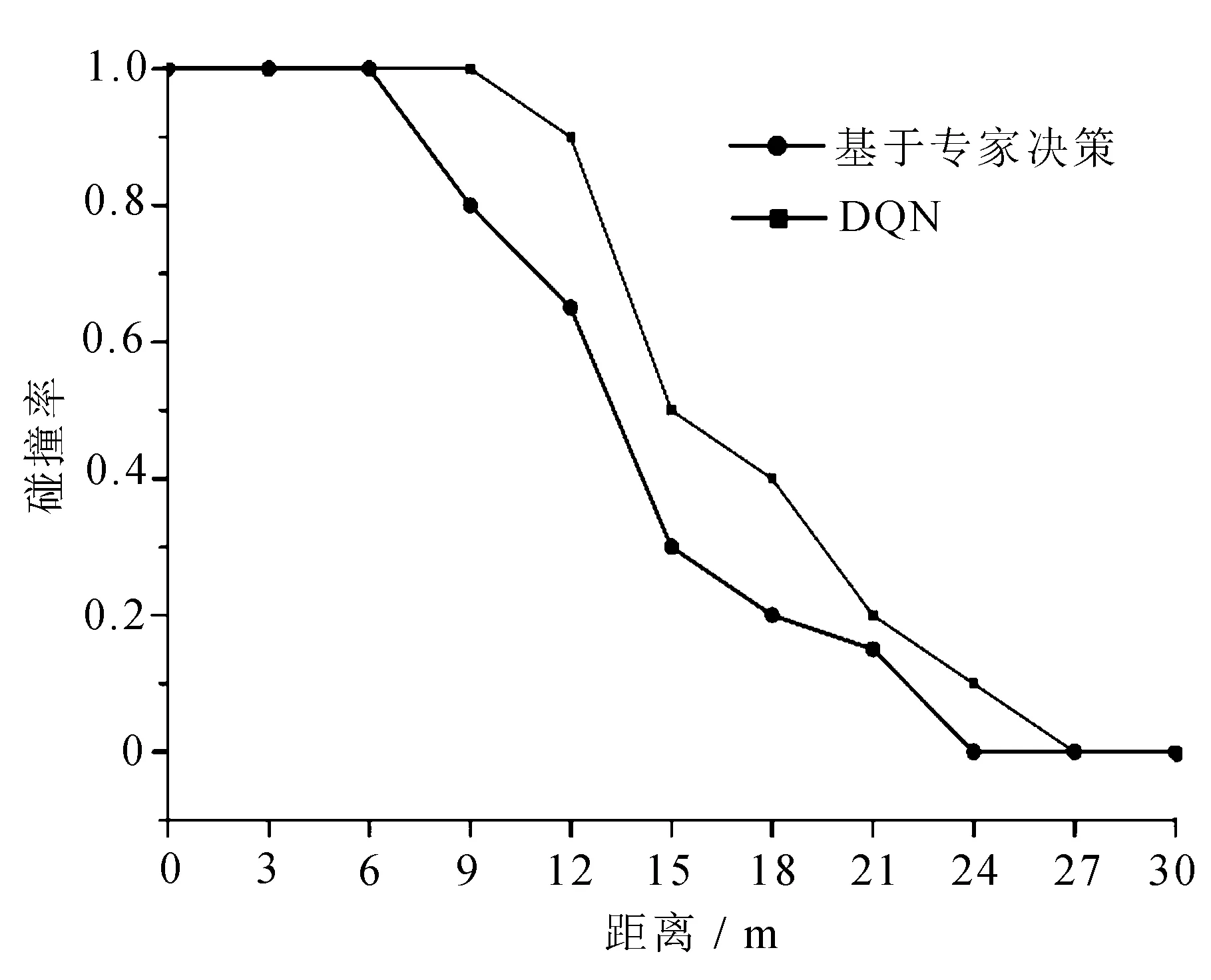
图8 距离路口不同距离下发生碰撞概率

在与路口相距不同距离下，实验车辆分别搭载两种方法发生碰撞的概率，基于DQN的紧急制动策略最大避免碰撞的距离为6 m，而基于专家决策的紧急制动策略的最大避免碰撞距离为9 m，在最大避免碰撞距离内，车辆碰撞率为100%。随着距离增加，两种方法碰撞概率下降，基于DQN紧急制动策略始终保持比基于专家决策的紧急制动策略更低的碰撞率。基于DQN的紧急制动策略完全避免碰撞的最小距离为24 m，基于专家决策的紧急制动策略完全避免碰撞的最小距离为27 m，在与路口距离大于最小避免碰撞距离时，可以完全避免产生碰撞，因此基于DQN的紧急制动策略，其避免碰撞距离与完全避免碰撞距离均小于基于专家决策的紧急制动策略，且在可能产生碰撞的距离内，碰撞概率始终小于基于专家决策的紧急制动策略，验证了所提出基于DQN的紧急制动策略的安全性。

4 结 语

基于DQN设计了基于深度强化学习的紧急制动策略,所设计策略与环境自主交互学习，在不同环境下实现自动紧急制动，基于Carla仿真平台与专家决策进行对比仿真验证，结果表明,所提出策略具有更高安全性。