基于车桥耦合振动的连续梁桥动力响应分析

彭伟康高庆飞徐昭若王统于晓梅

(1.哈尔滨工业大学 交通科学与工程学院,哈尔滨 150001;2.大连理工大学 建设工程学部,辽宁 大连 116024;3.东北林业大学 图书馆,哈尔滨 150040)

0 引言

车桥耦合振动(Vehicle-bridge Coupling Vibration)即为当车辆在桥梁上前进时,车辆由于车身与桥梁表面的接触和桥面的不平整度引起车身的振动,而桥梁又由于车辆的振动而引起桥体的振动,车辆与桥梁之间相互作用、相互影响,产生的车辆与桥梁之间的共同振动。

自19世纪初,英国第一条铁路桥梁修成以后,工程师们便开始发现车桥耦合振动方面的问题,并开始进行研究[1]。其早期的研究方法有试验研究法和古典解析法,自20世纪中期,随着电子计算机的发明,有限元技术的提出,数值模拟法也得到应用。数值模拟法的应用和发展,使得铁路桥梁的车桥耦合振动建立的模型更加贴近现实,振动响应的计算也更加接近实测。早期的车桥耦合振动研究几乎都是应用于铁路桥梁的,而随着近现代经济的发展和车辆的普遍使用,公路桥梁的车桥耦合振动问题也得到了越来越多的研究[2-4]。对于汽车-公路桥梁耦合振动的研究,最早可追溯到从19世纪末开始的试验研究法,相继有法国工程师、英国土木工程师协会和瑞士联邦材料科学与技术实验室进行了桥上动力荷载试验,并收集了大量汽车行车实测数据进行分析[5];20世纪80年代以来,国内也有吴启宏[6]、项贻强等[7]进行桥梁动力分析的试验研究,并获得动力系数、桥梁自振特性等结论。同时,为更好地认识车辆和桥梁之间的动力学关系,学者们的理论计算方法也投入使用,早期采用的计算方法有将车辆荷载简化为常量力、简谐力和滚动质量块等的解析计算法,通过多种解析计算方法的计算结果进行对比可知,车辆质量较大时车辆惯性力对于桥梁振动的响应有较大的影响[8]。公路桥梁的数值模拟法大约在20世纪70年代开始研究,国外及国内的学者均从车辆模型、桥梁模型和动力学方程求解3个方面进行不断的深入探索。对于车辆模型的建立,学者们最初使用的有四分之一车辆模型或二分之一车辆模型,近年来,为追求更高的模拟精度,国内外众多学者均建立了三维多自由度的车辆模型,如王铁龙等[9]、Obrien等[10]分别建立了三轴或五轴的卡车模型来进行车辆荷载的模拟;随着有限元软件的不断进步,桥梁模型的建立也在朝着完善的方向发展,从早期的杆系模型,空间梁格模型[9],到相对更加准确的实体模型,虽然实体单元模型能给中小跨径桥梁带来更高的精度,但也明显提高了较大跨径桥梁的计算规模,带来一定的计算压力,故多尺度模型[11]也可为大跨径桥梁带来一个重要的发展方向;依据桥梁与车辆的有限元模型,建立车桥耦合振动系统的动力学方程后,学者们求解动力学方程的方法可分为直接积分法和模态综合法,直接积分法可以将车辆动力学方程和桥梁动力学方程进行分组迭代求解[12],也可以将车辆动力学方程和桥梁动力学方程合并整体求解[13],模态综合法则将动力学方程进行振型叠加,简化自由度数目过大的动力学方程进行求解[9]。基于汽车-公路桥梁耦合振动的理论方法研究,动力放大系数可以较好地表征移动车辆对桥梁的冲击效应,同时也是各国桥梁规范中一个重要参数-冲击系数的计算方法。如今各国规范中所采用的冲击系数计算方法仍然存在较大的差异[14],众多学者的近期研究也认识到桥梁的冲击系数与桥梁结构类型、车速和车重等多种因素有关,各国规范所描述的冲击系数表示方法仍有一定偏差,需继续进行优化[15]。

本文主要阐述车桥耦合振动的基本理论与分析研究方法,并利用ANSYS软件对跨径为30 m×5 m的五跨连续梁桥进行车辆过桥的数值模拟,分别计算出桥梁在汽车静力荷载和动力荷载作用下的静力响应和动力响应,分析动力响应与静力响应比值(动力放大系数)的变化规律。对于桥梁的荷载响应而言,桥梁各个位置处的挠度、应力等均可作为其荷载响应,且每对动力响应与静力响应的比值也均可作为其动力放大系数,故本文也将从挠度、应力2个方面去分析标准桥梁的动力放大系数。

1 车桥耦合振动分析方法

车辆驶入桥梁以后,运动过程十分复杂,影响车桥耦合振动的因素很多,如车辆桥头跳车、行驶的变速(包括刹车)和路面的粗糙度等[16-18]。车桥耦合振动的分析方法有室内试验和现场试验的试验研究法、解析计算和数值模拟的计算研究法。现场试验研究实测所得的桥梁动力响应数据显然是最真实可靠的,众多学者[19-20]均进行了现场试验研究,然而仅靠现场试验研究来找到各种不同类型、不同尺寸桥梁在不同车辆行驶作用下的振动响应规律和其内运行机理,显然是不经济不现实的。相对于现场试验而言,室内试验可以较好控制车辆和桥梁的各项参数,能更好降低试验成本,反映车桥实际规律。解析计算即利用简单的简支梁、固端梁或者连续梁模拟桥梁,简单的常量力、简谐力、滚动质量块或者移动弹簧-质量块来模拟行驶车辆,建立简化模型进行理论推导,探寻车辆过桥动力响应基本规律。显然解析计算所得的简化计算结果与实际尚存在较大出入,但其为数值分析计算提供了理论基础。数值模拟分析计算即通过计算机来建立不同的桥梁与车辆的有限元模型,并通过对模型和模型之间的相互作用的数学表达来建立相关的动力学耦合方程,最后使用合适的微分方程解法完成动力学方程的求解,计算获得车桥动力响应特征。

1.1 数值模拟法

近些年对于车桥耦合问题,所采取的主要方法即为数值模拟法。进行数值模拟法,一般以刚体动力学方法建立车辆模型,以有限元方法建立桥梁模型,将车辆模型与桥梁模型分别作为2个子系统,再通过车轮与桥梁表面之间的位移协调、相互作用力大小相等的关系,使2个子系统的动力方程相联系,采用迭代法求解系统响应结果。其中车辆动力学模型由车体、车轮、弹簧和阻尼器组成,车轮与车体、车轮与桥面均由弹簧和阻尼器连接,车辆模型的自由度主要由车轮个数和车体个数来决定[21]。桥梁通过有限元模型进行模拟,有限无模型常用的单元类型有杆系单元、板壳单元和实体单元等,单元的选择应根据桥梁形状特征、受力特点和精度要求等因素综合考虑。各类不同的桥梁和不同的要求下,会有不同的桥梁建模类型,如:单梁或多梁的杆系模型、用等效梁格模拟上部结构的梁格模型、实体单元的精细化模型和局部小尺寸精细单元模拟的多尺度模型等[22-23]。

1.2 车桥耦合振动方程建立

进行数值模拟法的基本步骤为先建立车辆动力学模型,并建立车辆振动方程。车辆模型可拥有不同个数的车体,不同个数的轮轴,一般单个车体取浮沉、横移、点头和侧滚4个自由度,每个车轮取升降和横移2个自由度,通过拉格朗日方程即可推导出车辆运动方程

式中:Mv、Cv、Kv分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵;分别为车辆各个单元的位移向量、速度向量和加速度向量;Fv为桥梁与车辆接触点处对车辆的作用力向量。

继而建立合适的桥梁模型,并建立桥梁振动方程

式中:Mb、Kb分别为桥梁总体的质量矩阵和刚度矩阵,一般采用有限元方法建立,Cb为总体阻尼矩阵,一般通过质量矩阵和刚度矩阵计算获得;分别为桥梁各个单元的位移向量、速度向量和加速度向量;Fb为车辆作用在桥梁上的作用力向量。

然后将桥梁运动方程各模态坐标下动力响应叠加分析,化简桥梁的质量矩阵、阻尼矩阵和刚度矩阵,简化计算,得到模态综合分析下的桥梁结构运动方程

式中:MB、CB、KB分别为桥梁的质量矩阵、阻尼矩阵和刚度矩阵通过动力学方程的模态变换而得到的模态质量、模态阻尼、模态刚度矩阵;qB、FB则分别为桥梁有限元模型的广义位移向量和广义力向量。

联立车辆和桥梁振动方程,并考虑位移协调条件和相互作用力相等条件,便可得到如下车桥耦合振动方程

即为求解车桥耦合振动方程,其常使用的动力学方程求解方法为Newmark-β法。

2 有限元模型建立

本文选用《中国公路桥涵通用图》中常用的,具有代表性的装配式预应力混凝土连续T梁桥作为动力放大系数分析模型,桥梁为五跨连续梁桥,单跨跨径为30 m,广泛用于双向四车道,桥梁的横截面如图1所示。

连续梁桥利用ANSYS软件建立有限元模型,采用BEAM188单元建立桥梁的梁体,中间一处桥墩的位置设置纵向、竖向和横向3个方向的约束,其余桥墩或桥台位置处设置纵向和竖向2个方向的约束。同时为让有限元模型更贴近实际,本文采用梁格模型对5片T形梁之间的横向连接进行模拟,纵向设置5片T形梁截面之后,横向设置刚度相等、质量为零的虚拟横梁,纵梁与虚拟横梁共同承受车辆荷载作用。建立所得的有限元模型如图2所示。

图1 多跨连续梁桥横截面Fig.1 Cross section of multi-span continuous girder bridge

图2 ANSYS有限元模型Fig.2 ANSYS finite element model

基于ANSYS软件建立的桥梁有限元模型,首先在模型中梁的各跨跨中施加车辆静力荷载,设置车辆荷载为30 t,桥梁混凝土弹性模量为3.45×104MPa,分析计算得5片单梁的各跨跨中挠度,计算结果见表1。同时分别利用ANSYS软件计算得到有限元模型在中梁各跨跨中施加静力荷载时所产生的应力云图,计算结果如图3—图5所示。

式中：i为年份，j为指标序号，aij为指标数据原始值，bij为标准化值，amax、amin分别为第j指标的最大值和最小值。

从桥梁的有限元模型在静力荷载作用下所产生的3个应力云图可以看出,在重力作用下边跨处产生最大应力,中跨次之,次边跨处最小;车辆荷载作用在边跨时产生的桥梁最大应力为7.13×106N/m2,作用在次边跨时产生的桥梁最大应力为6.55×106N/m2,作用在中跨时产生的桥梁最大应力为5.60×106N/m2,可见边跨处荷载产生的应力最大。

表1 中梁各跨跨中施加静力荷载的挠度Tab.1 Deflection caused by static load applied in each span of the center beam mm

图3 一跨跨中车辆荷载作用下应力云图Fig.3 Stress nephogram under vehicle load in first span

图4 二跨跨中车辆荷载作用下应力云图Fig.4 Stress nephogram under vehicle load in second span

图5 三跨跨中车辆荷载作用下应力云图Fig.5 Stress nephogram under vehicle load in third span

通过静力荷载作用下的桥梁挠度数据和应力云图结果分析可知:桥梁在大型货车的荷载和自重荷载的作用下,可以产生的最大静挠度约为11 mm;在自重荷载的作用下,边梁的跨中挠度最大,次边梁的跨中挠度最小;在中梁的各跨跨中施加静力荷载,可以得到施加荷载的桥梁跨中位置处中梁挠度最大,次边梁略小,边梁最小。由此可确定桥梁模型受力特性符合实际情况。

3 数值仿真结果

3.1 动力放大系数计算

动力放大系数即为桥梁在汽车动力荷载和汽车静力荷载作用下最大动力响应与最大静力响应的比值,本文选用五跨连续梁桥,分别选取其边跨跨中、次边跨跨中和中跨跨中3个位置的最大荷载响应进行研究,计算并比较其动力放大系数[24-25]。

动力放大系数计算即利用ANSYS软件进行有限元分析可得到桥梁3个跨中位置在车辆经过桥梁时所产生的荷载效应,本文对3个跨中位置处的挠度、应力2个荷载效应分别进行研究,滤去产生荷载效应中的桥梁自重荷载,比较其车辆动力荷载效应和最大静力荷载效应[26]的比值。图6为五跨连续梁桥在车辆静载作用下的中跨跨中挠度随车辆位置变化的曲线(静挠度),和车辆以20 m/s行驶过桥梁时中跨跨中挠度随行驶距离变化的曲线(动挠度)。计算的结果中提取相应的最大静挠度和最大动挠度,同时减去桥梁自重产生的挠度,即可得到汽车荷载最大静挠度和最大动挠度,求取比值即为动力放大系数。本文中3个跨中位置处的4种荷载效应下的动力放大系数计算方法均相同。

3.2 车辆频率对动力放大系数的影响

车辆模型的车体通过弹簧阻尼器与桥梁模型进行连接,车辆的振动频率与车体的质量、弹簧阻尼器的刚度等有关,若改变车体的重量,不仅改变了车辆的频率,也改变了车辆荷载的大小,不能独立研究单一因素对动力放大系数的影响。本文取车体质量为30 t,分别取弹簧阻尼器的刚度为1×105、2×105、3×105、4×105

图6 中跨跨中动静挠度曲线Fig.6 Dynamic and static deflection curve of midspan

、5×105N/mm,即可计算得出相应车辆的振动频率分别为2.906、4.109、5.033、5.812、6.498 s-1。故通过改变车辆的弹簧阻尼器的刚度,来改变车辆频率,从而得到不同跨中位置处多种荷载响应的动力放大系数变化规律,分析结果如图7—图9所示。

图7 车辆频率对中梁动力放大系数的影响Fig.7 Influence of vehicle frequency on dynamic amplification factor of center beam

图8 车辆频率对次边梁动力放大系数的影响Fig.8 Influence of vehicle frequency on dynamic amplification factor of secondary side beam

图9 车辆频率对边梁动力放大系数的影响Fig.9 Influence of vehicle frequency on dynamic amplification factor of side beam

由图7—图9可知,中梁和次边梁在不同的跨中位置,不同的荷载效应下得到的动力放大系数均在车辆频率为4～5 Hz时取得最大值,经模态分析可得,桥梁频率为4.44 Hz,此时车辆频率与桥梁频率十分接近,显然车桥间产生的共振效应是此时产生最大动力放大系数的原因。然而计算所得边梁处的动力放大系数却随着车辆频率的递增呈现衰减的趋势,且冲击系数的计算结果在车辆频率较小时取值较大,能达到接近2.5的挠度冲击系数。其次,对于所有的T形梁而言,在大多数情况下,边跨跨中产生的动力放大系数均大于中跨跨中和次边跨跨中,而中跨跨中和次边跨跨中的动力放大系数则大小接近,尤其当车辆频率较大时,3个不同跨中位置处的动力放大系数大小均较为接近。

3.3 桥梁频率对动力放大系数的影响

由图10—图12可知,对于中梁而言,随着桥梁频率的增加,边跨跨中在不同的荷载效应下得到的动力放大系数均在稳步下降,而次边跨跨中和中跨跨中的动力放大系数则在挠度效应下先降后升,在应力效应下先升后降。而对于次边梁而言,随着桥梁频率的增加,边跨跨中在不同的荷载效应下得到的动力放大系数均在稳步下降,而次边跨跨中和中跨跨中的动力放大系数则在挠度效应和应力效应下均呈现先降后升的趋势。对于边梁,其动力放大系数却随着车辆频率的递增呈现衰减的趋势,且边梁处的动力放大系数相比于中梁和次边梁明显较大。同时,也可看出3个不同跨中位置的动力放大系数值均随着桥梁频率的增加而更加接近。且对于不同的荷载效应下,跨中挠度动力放大系数能取最大值,均远大于应力效应下的动力放大系数。

图10 桥梁频率对中梁动力放大系数的影响Fig.10 Influence of bridge frequency on dynamic amplification factor of center beam

图11 桥梁频率对次边梁动力放大系数的影响Fig.11 Influence of bridge frequency on dynamic amplification factor of secondary side beam

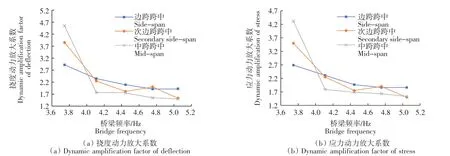
图12 桥梁频率对边梁挠度动力放大系数的影响Fig.12 Influence of bridge frequency on deflection dynamic amplification factor of side beam

3.4 扰动频率与桥梁频率比值对动力放大系数的影响

图13 扰动频率与桥梁频率比值对中梁动力放大系数的影响Fig.13 Influence of disturbance frequency/bridge frequency on dynamic amplification factor of center beam

车辆对桥梁的扰动频率与车辆行驶速度和桥梁的跨径有关,同理,为了不影响中国公路通用图中的桥梁标准结构,此处通过改变车辆的行驶速度来研究动力放大系数随扰动频率与桥梁频率的比值变化的变化规律,所使用的行车速度分别为10、15、20、25、30 m/s,计算所得的扰动频率与桥梁频率比值分别为0.047、0.071、0.094、0.118、0.141,动力放大系数分析计算结果如图13—图15所示。

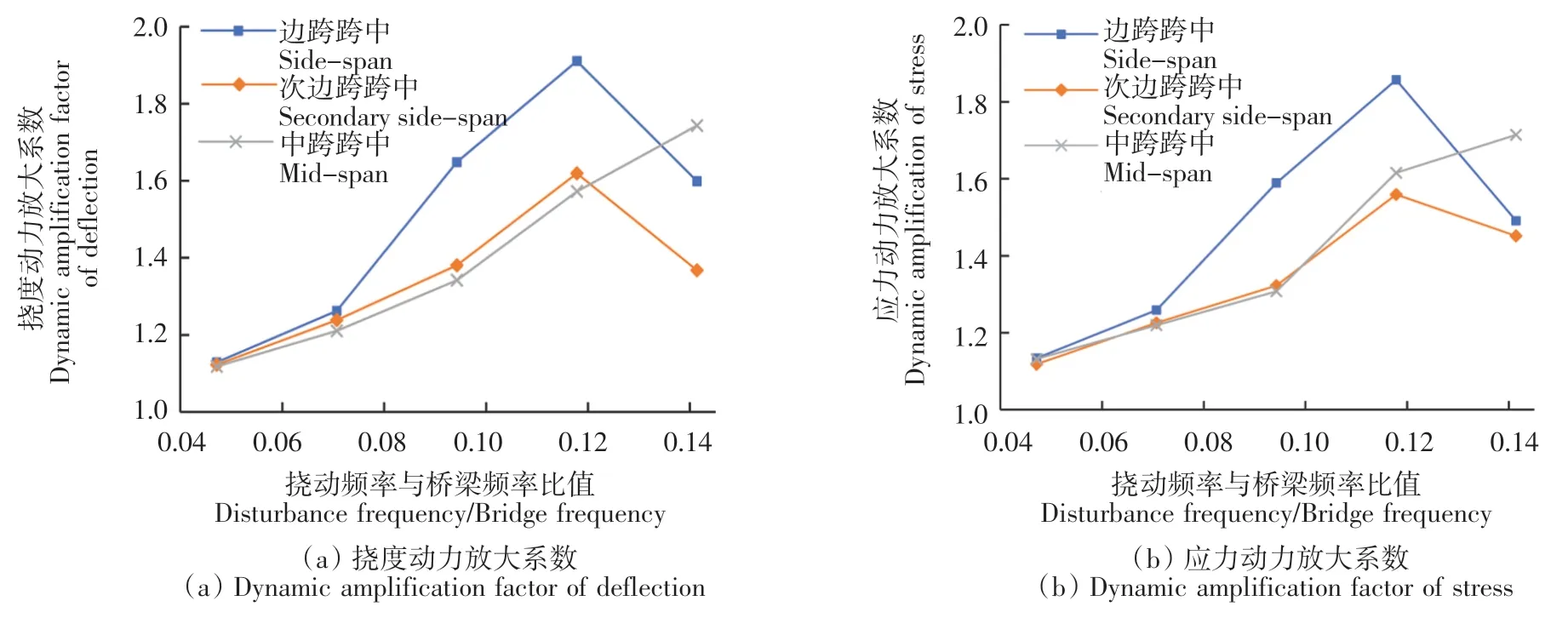
图14 扰动频率与桥梁频率比值对次边梁动力放大系数的影响Fig.14 Influence of disturbance frequency/bridge frequency on dynamic amplification factor of secondary side beam

图15 扰动频率与桥梁频率比值对边梁动力放大系数的影响Fig.15 Influence of disturbance frequency/bridge frequency on dynamic amplification factor of side beam

由图13—图15可知,对于所有的T形梁而言,随着扰动频率与桥梁频率比值(行车速度)的增加,边跨跨中和次边跨跨中在不同的荷载效应下得到的动力放大系数均为先升后降,且均在行车速度为25 m/s左右时达到顶点,而中跨跨中的动力放大系数则在不同的荷载效应下均为缓慢上升。同时,也可看出3个不同跨中位置的动力放大系数值均在车速较小时十分接近,随着车速的增加而产生相对的差异。边梁计算所得的动力放大系数虽变化趋势与中梁和次边梁相近,但边梁的动力放大系数取值却均远大于中梁和次边梁,最大的动力放大系数可达到5.8。

4 结论

车辆桥面行驶产生的动力响应有多种表现形式,本文基于车桥耦合振动理论,对车辆荷载作用下,多跨连续梁桥不同位置处挠度、应力2个动力响应的动力放大系数进行影响因素分析,得到的主要结论如下。

(1)当车辆频率与桥梁的基频接近时,将会产生共振的效果,此时在边跨跨中、次边跨跨中和中跨跨中等位置均会产生较大的动力放大系数。

(2)在不同的影响因素作用下,不同的荷载效应计算,所得的中跨跨中位置和次边跨跨中位置处动力放大系数变化规律和数值大小均较为接近,而与边跨跨中位置处的动力放大系数则存在一定的差异,说明边跨处一端简支的结构对此处的动力放大系数存在较大的影响。

(3)通过对桥梁多片主梁的动力放大系数进行分析,可以看出桥梁的边梁相对于其中梁和次边梁存在较大的差异,如边梁的动力放大系数随车辆频率的变化趋势与中梁和次边梁明显存在差异;边梁的动力放大系数数值大小相较于中梁和次边梁取值较大。

(4)本文有限元分析可以看出,车辆荷载不同响应的动力放大系数大小与变化规律均存在差异,且车辆频率、桥梁频率、行车扰动频率等均对动力放大系数产生影响,故公路桥梁规范中的冲击系数仅作为桥梁基频的函数,与实际有较大的差距,有待改进。