道路综合管廊输水管道参数辨识研究

孙强张智霖伍悦滨徐莹

(1.东北林业大学 土木工程学院,哈尔滨 150040; 2.东北林业大学 人工环境控制与能源应用研究所,哈尔滨 150040; 3.哈尔滨工业大学 建筑学院,哈尔滨 150090; 4.哈尔滨工业大学 寒地建筑科学与工程研究中心,哈尔滨 150090;

5.哈尔滨商业大学 能源与建筑工程学院,哈尔滨 150028)

0 引言

在城市道路综合管廊长距离输水管道系统中,高分子聚合物管材应用愈来愈广泛,并逐渐取代传统弹性管材(如镀锌钢管和铸铁)[1-2]。这类高聚物管材,又称其为黏弹性管道,相较于传统管材而言,兼具黏性和弹性力学行为[3-5]。当综合管廊管路系统中因水泵突然启停而发生停泵水锤时,黏弹性管道动力学行为与弹性管道截然不同,管壁应变出现延迟,这导致黏弹性瞬变流过程中波速降低、压力峰值减小、压力波相位延迟。因此,准确描述综合管廊长距离输水管道水力瞬变动力学行为是十分必要的。

要准确描述综合管廊黏弹性管道瞬变流压力波动,需要确知本构参数,因此,黏弹性管道本构参数辨识在瞬变流数值计算中非常重要。对于黏弹性管道本构参数辨识的研究,许多学者通常是借助优化算法(如最小二乘估计[6]、遗传算法[7-8]等)对本构参数进行辨识。Covas等[6,9]利用最小二乘法辨识本构参数,并分析了K-V元件个数对于辨识结果准确性的影响。研究表明,3个及以上的K-V元件个数对于辨识结果准确性的影响较小。Pezzinga等[7-8]利用微遗传算法辨识本构参数,研究表明KV元件个数过多时,无法确知本构参数与压力波动周期间的关系。Gally等[10]基于力学拉伸实验确定管材本构曲线,数值计算得到较好结果。此外,本构参数的辨识对不同管长[11-12]、摩阻模型[13-14]以及气液两相流[15-16]等情况下的黏弹性管道瞬变流的数值计算研究也产生重要影响。

对于辨识问题采用的优化算法来说,最小二乘估计由于其简便性可能存在一定误差,而遗传算法辨识准确,但却过于复杂,对工程而言耗时较长。因此,本研究基于一种简便且精确的优化算法——序列二次规划(Sequential Quadratic Programming ,SQP),利用一维拟稳态摩阻模型结合Kelvin-Voigt(K-V)模型,辨识综合管廊黏弹性管道本构参数(蠕变柔量和延迟时间),并就不同温度下的本构曲线和压力曲线辨识结果进行讨论,揭示不同温度下辨识结果的影响机制。

1 辨识模型的构建

城市道路综合管廊黏弹性管道参数辨识模型的构建基于黏弹性管道瞬变流模型结合K-V力学模型和一维拟稳态摩阻模型,以实验数据与数值计算结果的压力差值平方和最小为目标,给定本构参数的约束条件,采用优化算法进行求解的过程。

1.1 黏弹性管道瞬变流控制方程

一维黏弹性管道瞬变流控制方程由连续性方程和动量方程组成[17-19]

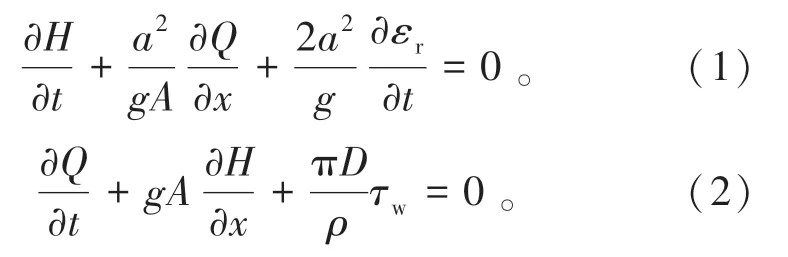
其中,稳态管壁剪切应力用Darcy-Weisbach公式表示为

式中:H为管道内压力水头,m;Q为流量,m3/s;a为波速,m/s;εr为管道的延迟应变;V为平均流速,m/s;τw为剪切应力,Pa;x为轴向距离,m;t为时间,s;g为重力加速度,m/s2;ρ为流体密度,kg/m3;f为摩擦系数;D为管道直径,m;A为管道横截面积,m2。

1.2 黏弹性管道本构模型

本研究所采用的黏弹性本构模型为K-V力学模型,如图1所示,该模型[20-21]由1个弹性单元和N个黏弹性单元串联构成,其中弹性单元由弹性元件弹簧表示,遵循虎克定律,黏弹性单元由N个弹簧和黏壶并联组成的K-V元件构成,用于描述黏弹性管道的蠕变和松弛特性。

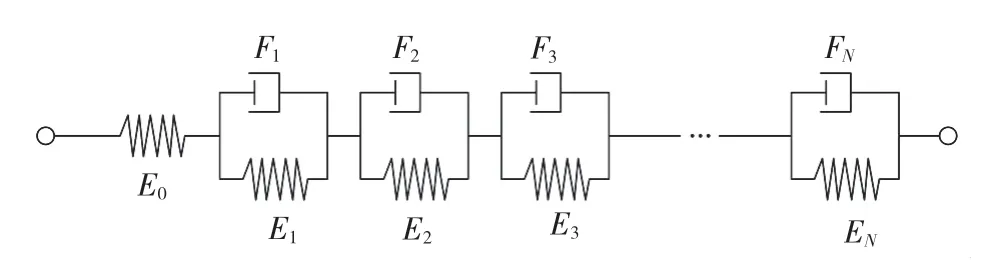
图1 K-V力学模型Fig.1 Kevin-Voigt model

采用K-V模型,应用拉普拉斯变换,蠕变函数可表示为

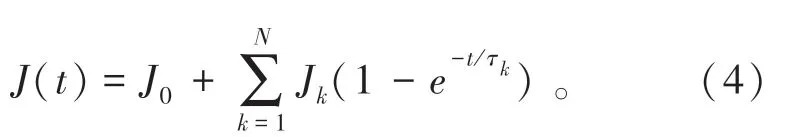
式中:J0为瞬时柔量,J0=1/E0,E0为瞬时弹性模量;Jk为第k个K-V元件的蠕变柔量,Jk=1/Ek,Ek为第k个弹簧的弹性模量;τk=Fk/Ek为第k个黏壶的松弛时间;Fk为第k个K-V元件中黏壶的黏性系数;e为壁厚。

1.3 本构参数辨识方法

基于已知测点的瞬变流压力波动数据,采用SQP算法,通过对实验与模拟的压头之间差的平方和建立目标函数,实现误差最小化,辨识黏弹性管道本构参数。其数学关系式如下

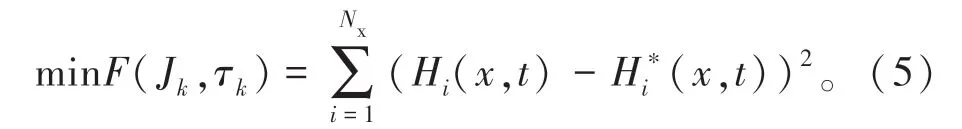
式中:Hi为模拟压力水头;H*i为实验压力水头;Nx为节点总数。

约束条件:每个K-V元件的蠕变柔量Jk和延迟时间τk在合理的数量级范围内。

SQP算法是非线性规划算法中的一类特殊数学规划问题,利用泰勒级数将目标函数在迭代点处简化为二次函数,将约束条件简化为线性函数的一种求解最优解问题的算法[22-23]。通过给定初始值、收敛精度,在约束范围内进行遍历搜索,直到找到满足精度的最优解,结束算法。SQP算法收敛性好、计算效率高、边界搜索能力强,但在应用此算法进行辨识求解时,需注意初始点的选取应结合工程实践经验给出。

该辨识方法的具体过程,如图2所示。根据图2做以下分析。

(1)确定待辨识的黏弹性管材基本信息,包括管长(L)、流速(V)、管径(D)、壁厚(e)、密度(ρ)、阻力系数(f)和初始压力(H0)。

(2)采用特征线法求解瞬变流模型,确定压力H。

(3)确定黏弹性管道本构模型中K-V元件个数。本文根据Covas等[6,9]给出的建议值,选取3个元件的K-V模型。

(4)确定瞬变流压力波的波速。

其波速计算公式采用如下公式

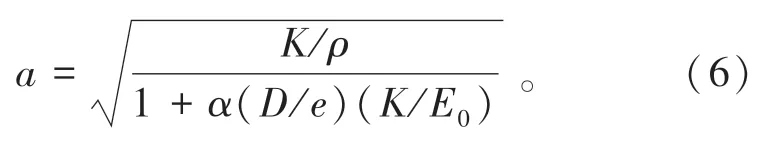
式中:νp为泊松比;K为流体体积模量,Pa;E0为弹性管道杨氏模量,Pa。

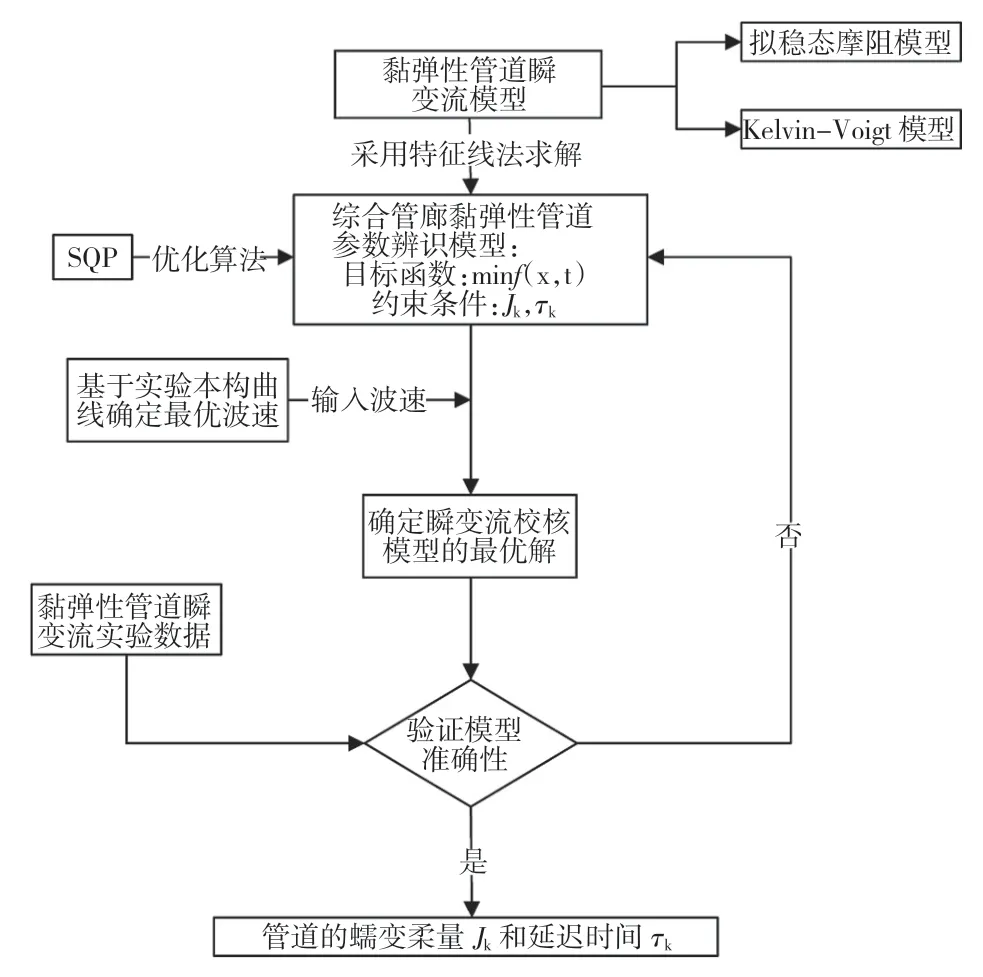
图2 本构参数辨识流程路线图Fig.2 Flow diagram of calibration of constitutive parameters

(5)用SQP算法辨识本构参数,即管道的蠕变柔量Jk和延迟时间τk。

2 试验与数据

本文采用Gally等[10]所设计的黏弹性管路水力瞬变流室内实验,该实验装置是一个由定压罐、低密度聚乙烯管和末端快关阀门组成的输水系统,如图3所示。实验管道总长43.1 m,管内径41.6 mm,壁厚4.2 mm。管路的两端用固定支架固定。定压罐体积为15 m3,上下游敞口水箱的体积分别为9 m3,其中上游水箱配有加热和水温控制装置。另外,该实验的蠕变曲线由Gally等[10]通过流变振动仪进行动态测试所得,在限定的频率范围(0.1～11 Hz)内直接测量输水管路的应力和应变,通过测得储能模量E1和内摩擦角δ,最终数值计算求得蠕变曲线[10,24]。

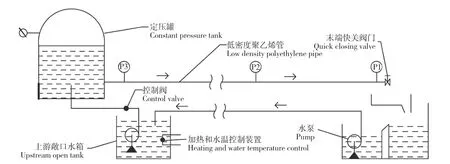
图3 实验装置示意图[24]Fig.3 Schematic diagram of the experimental setup

实验通过加热和水温控制装置对水箱中流体加热,从而进行不同温度下的末端关阀实验,关阀时间12 ms,3个高精度压力传感器安装在管路的上中下游,记录不同位置的瞬变流压力,具体实验参数见表1。本文主要分析下游末端阀门处的压力变化情况,为道路综合管廊输水管道参数辨识提供指导。

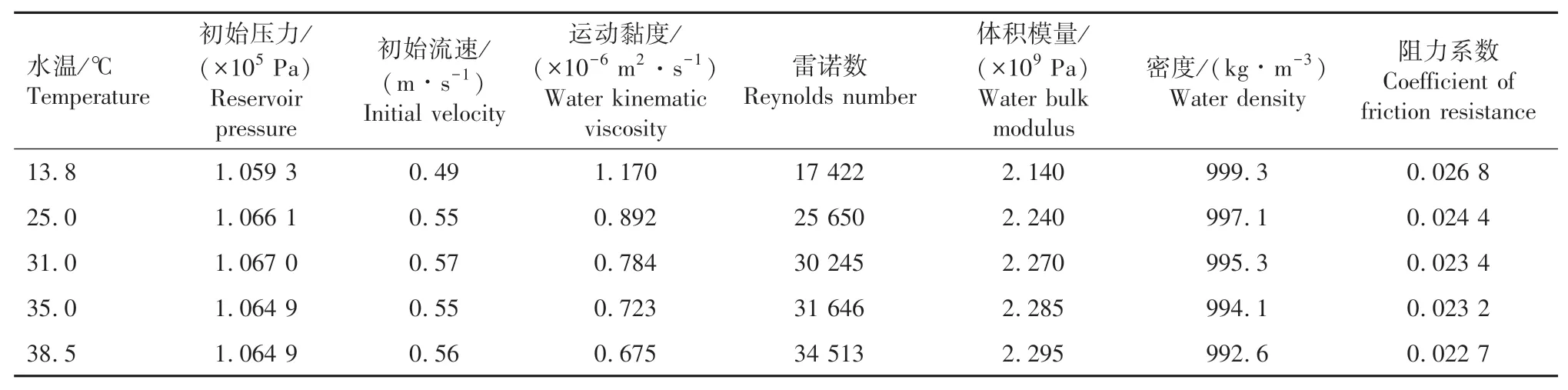
表1 不同情况下的实验数据[24]Tab.1 Experimental data for different cases

3 结果与分析

3.1 波速的确定

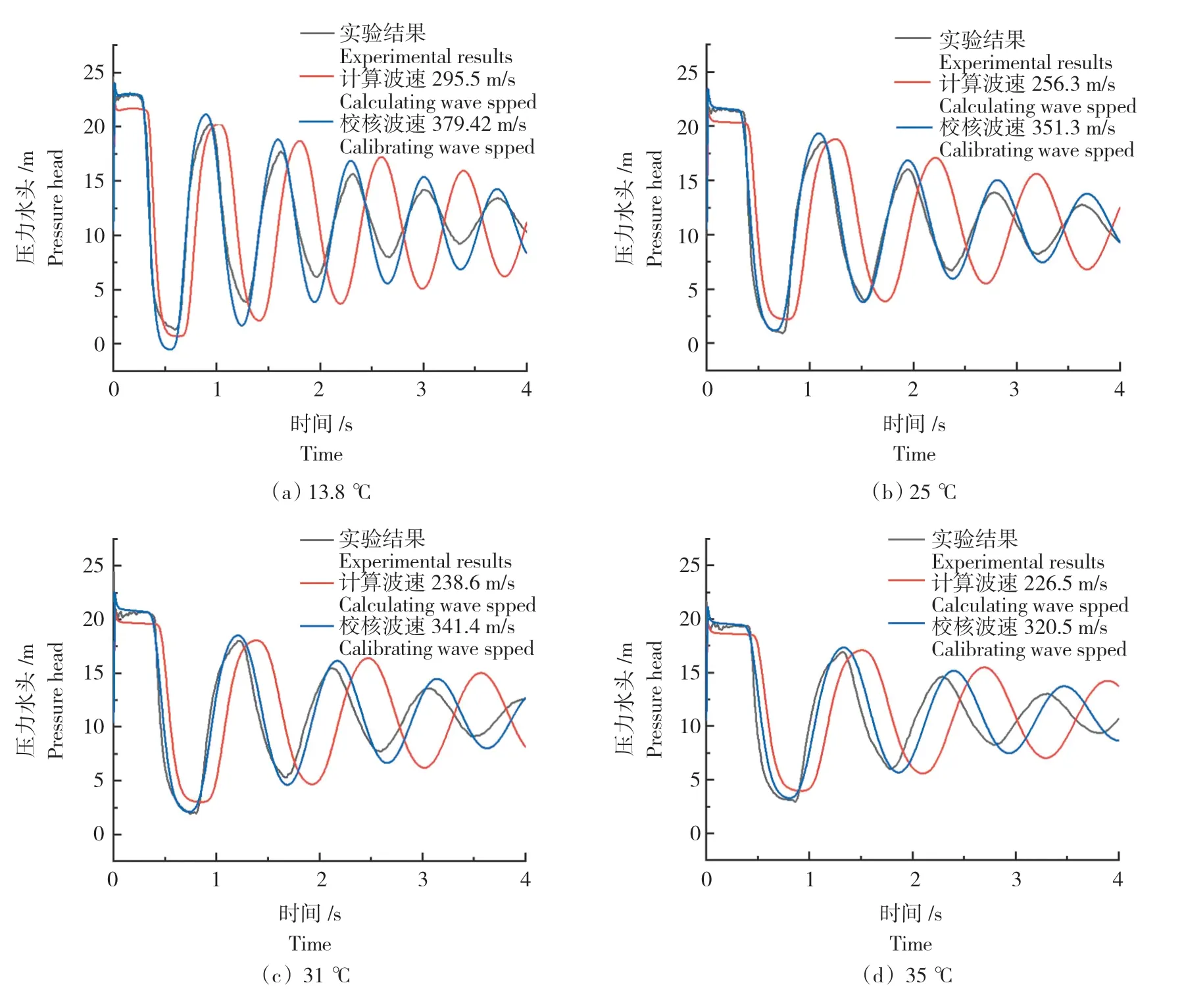
从理论计算波速的模拟结果可以看出,模拟与实验之间的误差较大。故波速的数值仍需进行校核。本研究的计算波速参考文献[23],基于实验所测得的本构曲线,将计算得到的波速进行试算,考虑到一维拟稳态摩阻模型的局限性,仅考虑压力波第一个峰值的拟合情况,最终确定13.8 ℃时压力波波速为379.42 m/s,25 ℃时压力波波速为351.3 m/s,31 ℃时压力波波速为341.4 m/s,35 ℃时压力波波速为320.5 m/s,38.5 ℃时 压力波波速为315.4 m/s。同时,在瞬态流动数值模拟中,将管道划分为64个等长单元(Nx=64)。图4为不同水温情况下计算波速的校核结果。由图4可以看出,经过校核得到的压力波波速在描述第一个压力波动峰值时较准确,可以用来作为初始波速进行后续的综合管廊黏弹性管道本构参数辨识。

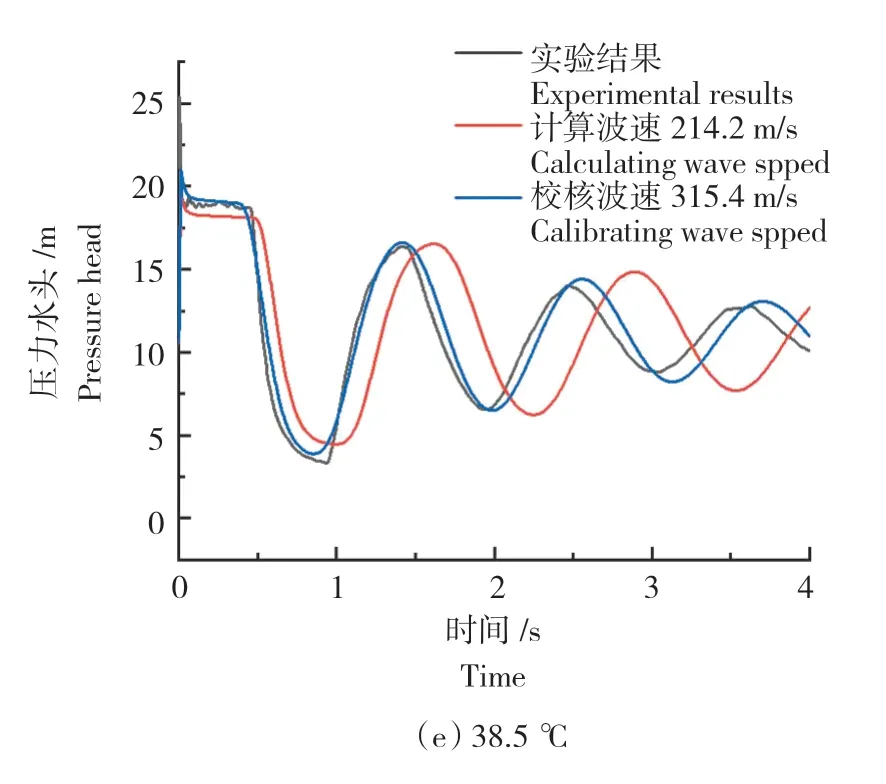
图4 不同温度下波速的校核结果Fig.4 Calibration of wave speed at different water temperatures

3.2 本构曲线

图5为不同水温的本构曲线辨识结果。由图5可以看出,在不同水温下,综合管廊黏弹性管道的本构特性是不相同的,其蠕变函数受水温的影响较大,且随着水温的升高,管道的蠕变参数逐渐增大。蠕变曲线辨识结果与实验数值计算的结果存在一定的差异,这与黏弹性管道本身的应力应变历史积累有一定关系。同时管道瞬变流实验压力波与模拟压力波存在时间上的不同步性,以及压力波波速在辨识过程中的差异,都导致了两者之间的差异。

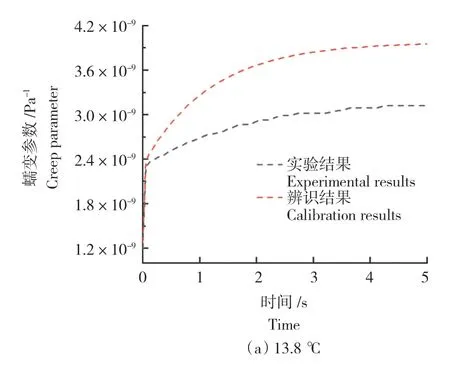
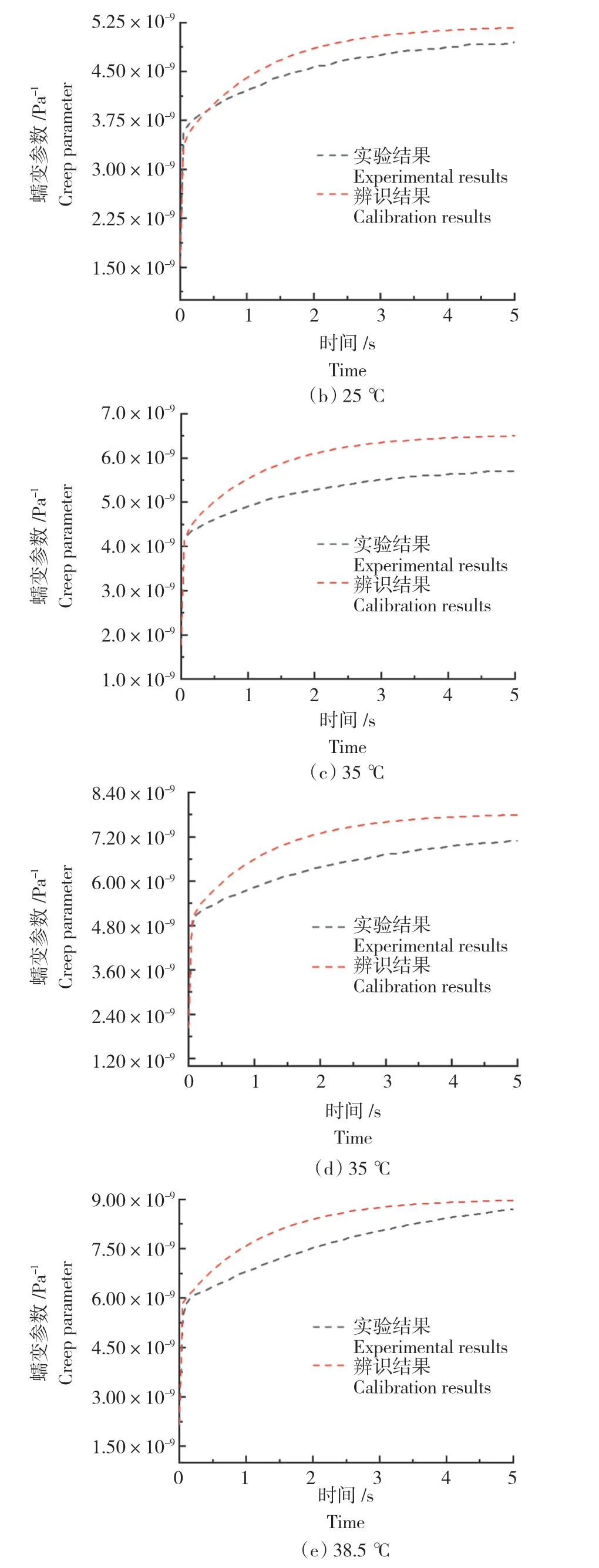
图5 不同温度下蠕变参数辨识结果Fig.5 Calibration of creep parameters at different water temperatures

另外,通过对实验的蠕变曲线观察可知,蠕变函数在0～0.07 s内数值陡增,随后管道蠕变曲线随时间缓慢增加,不同水温的管道蠕变曲线最大值出现时间不同并且数值也不同。水温为13.8、25、31 ℃的蠕变曲线,在4 s左右达到最大值,水温为35 ℃和38.5 ℃的蠕变曲线,在5 s左右达到最大值。

3.3 压力波动曲线

不同温度下压力波动计算结果,如图6所示。由图6可以看出,当水温为13.8 ℃时,辨识出的压力波动峰值和谷值均低于实验结果。当水温为25 ℃时,数值计算的第一个压力峰值略高于实验结果,其后的压力峰值略高于实验结果。当水温为31、35、38.5 ℃时,压力波动的峰谷值及相位的计算结果与实验结果趋于吻合。

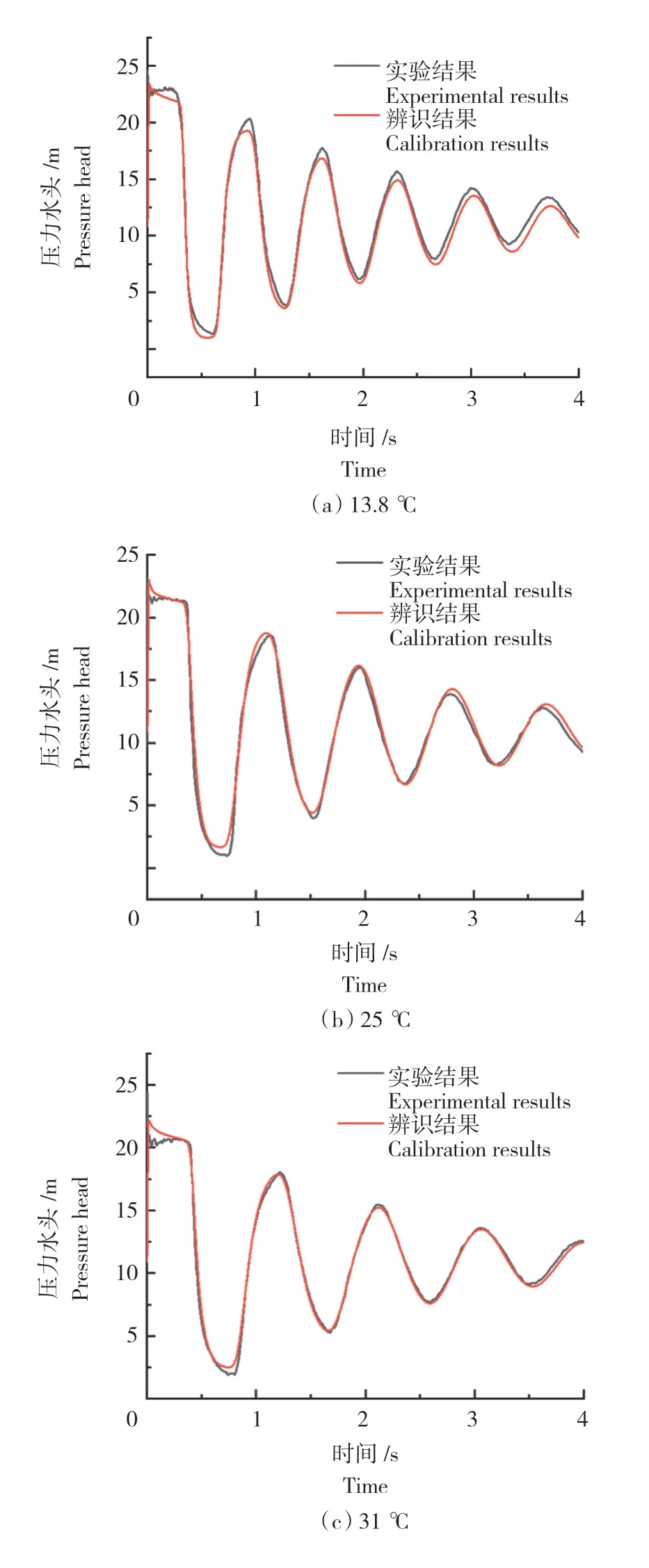
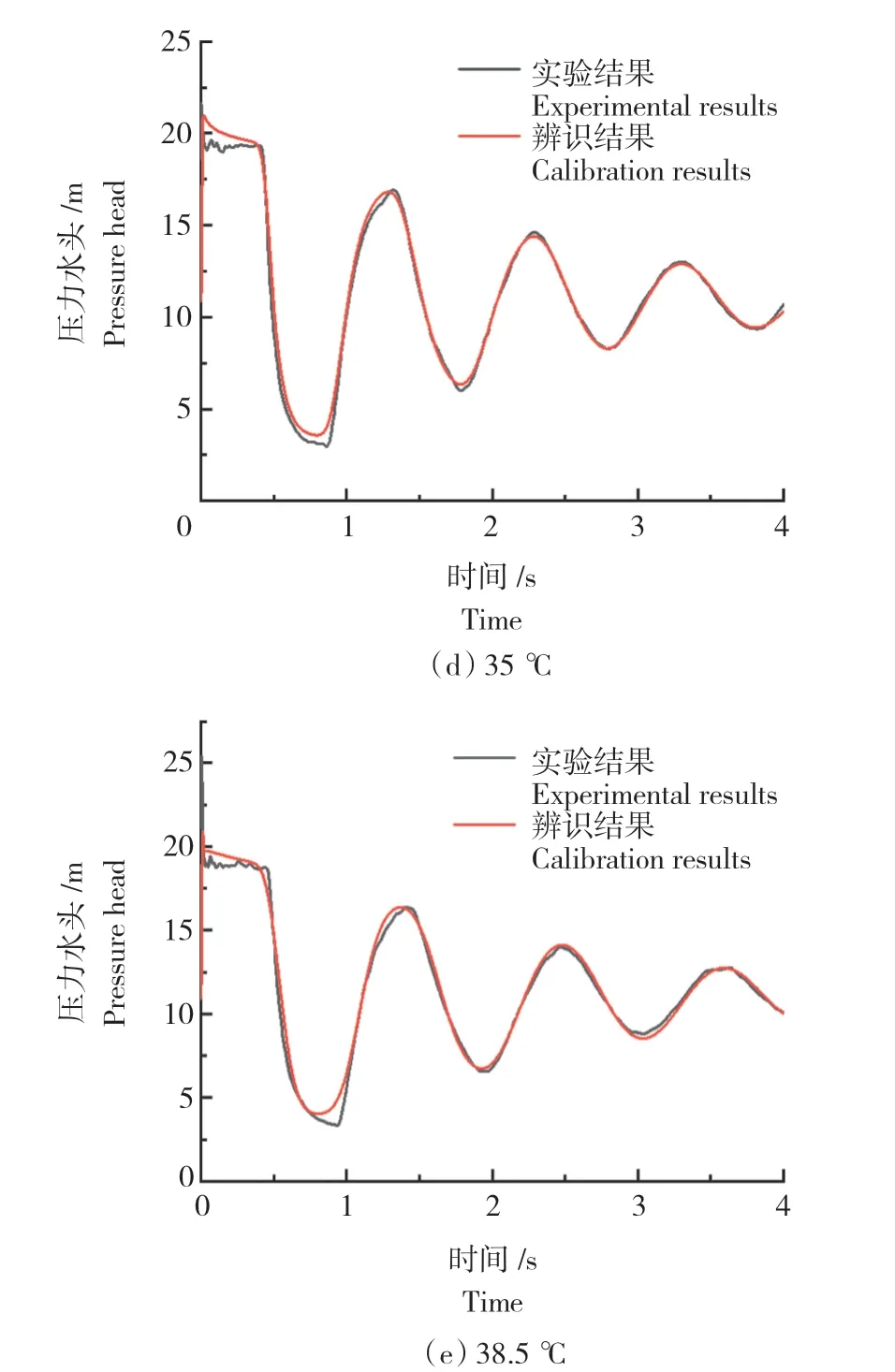
图6 不同温度下压力曲线辨识结果Fig.6 Calibration of pressure curve at different water temperatures

对比不同温度下的结果可知,随着水温升高,数值计算的压力波动结果更趋近于实验数据,这是由于本构曲线辨识过程中,摩阻项的影响越来越小、相应的管道黏弹性项的影响越来越大所导致的[21,25]。

4 结论

本文提出了一种基于瞬变流分析的综合管廊黏弹性管道本构参数辨识方法,并讨论研究了不同温度下辨识结果的差异。

(1)SQP算法能够快速准确辨识本构曲线,相比于实验的本构曲线,得到了较准确的本构参数,同时压力曲线的计算结果与实验压力结果接近。

(2)基于黏弹性管道瞬变流模型,结合一维拟稳态摩阻模型,所提出的本构参数辨识模型,可较准确辨识综合管廊管道本构参数。

(3)通过对不同水温下的本构曲线进行分析可知,蠕变函数受温度的影响较大,且随着水温的升高,综合管廊管道的蠕变参数逐渐增大,并且城市道路综合管廊黏弹性管道参数辨识模型模拟压力波动结果在峰值和相位上更接近实验结果。