典型膨胀土应力应变归一化特性分析

王 飞，张有桔，彭世龙，张 挺，曹广勇

(1.安徽省交通规划设计研究总院股份有限公司 公路交通节能环保技术交通运输行业研发中心,安徽 合肥 230088；2.安徽建筑大学 a.建筑结构与地下工程安徽省重点实验室；b.安徽建筑大学 土木工程学院，安徽 合肥 230601)

膨胀土的力学特性是工程建设过程中无法避免的基础问题，国内外学者采用理论分析和室内试验等方法已对不同类型土体的应力-应变特性开展了大量的研究。由于天然沉积形成的原状土体，受温度、围压、干湿状态、应力路径和结构性等影响，会表现出复杂的力学特性，很难用一个统一合理的数学公式来描述土的应力应变曲线。为此，一些学者在软土和砂土等研究中采用不同的归一化因子来分析相应土应力-应变曲线的归一化特性，取得了较好的效果。孔令伟[1]对武汉地区的软土进行三轴CU试验，探究了武汉软土的应力应变类型，并使用偏应力渐进值作为归一化因子；李向东[2]通过中密砂三轴试验，得到其在常规围压范围下的归一化特性，并探究出一种合适的归一化因子，建立起神经网络本构模型；常丹[3]针对冻结粉细砂的应力应变特性，提出一种新的归一化因子来分析粉细砂在冻融循环作用下的归一化特性；肖桂元[4]通过制备不同压实度的红黏土作为试验对象，发现在不同压实度下红黏土有两种应变类型，并发现应力应变归一化因子用偏应力渐进值效果最佳。膨胀土作为一种分布广泛的特殊性质黏土，目前对其应力应变特性的归一化研究较少，因此选择合理的归一化因子来建立膨胀土应力应变归一化方程，对膨胀土地区的工程实践有着较强的指导意义。

本文基于ETAS三轴试验系统，以合肥地区典型地层膨胀土为研究对象，开展了不同围压下的膨胀土三轴试验，得到不同围压等级下的应力应变曲线，研究其应力应变特性，并基于Kondner双曲线模型，采用归一化分析方法，建立了以破坏应力为归一化因子的膨胀土归一化方程，对合肥地区膨胀土进行归一化分析，获得相应的归一化参数。

1 膨胀土应力应变三轴试验

本次试验所选土样为合肥地区典型膨胀土，取土深度在17～25 m，颜色为黄色和黑褐色，天然状态下大部分处于硬塑状态，具有反复胀缩的特性，主要成分是蒙脱石和高岭石等亲水性矿物质。所取膨胀土的基本物理性质指标如表1所示。

表1 土的基本物理性质指标

按《土工试验标准》(GB/T50123—2019)要求[5]，制备尺寸为50mm×100mm，含水率为15%的膨胀土标准试样，试验设备采用ETAS全自动环境三轴试验系统，该系统中高级加载模块和标准三轴模块，可精准实现本试验所需的固结和三轴加载实验过程，并实时采集数据。

为研究不同应力水平作用下膨胀土变形特性，固结不排水三轴试验分别进行4个围压水平，依次为100、200、300、400 kPa，试验围压采用各向等压加载方式，剪切过程加载方式为应变控制式，轴向加载速率为0.2 mm/min，其加荷过程如图1和表2所示。

图1 三轴加荷应力过程

表2 三轴加荷试验方案

2 试验结果及其归一化特性分析

2.1 应力应变关系及强度特性分析

图2为常规三轴加载过程中膨胀土应力-应变曲线，经分析发现，不同应力水平作用下膨胀土常规加载应力应变曲线均呈双曲线型，表现为典型应变硬化特征，为应变硬化型土。加载过程中，应力应变曲线初段随着应变的增加，主应力差随之迅速增加，在应变达到3%之后，主应力差值增长速率逐渐趋于平缓。

图2 常规加载条件下应力-应变曲线

在相同的破坏应变下(本试验取轴向应变为12%时)，膨胀土破坏应力随初始固结应力增加而增大；由于低应力状态下，膨胀土初始孔隙率较小，随着围压的增加，在初始固结过程中，试样孔隙挤密效果逐渐降低，因此，在围压较小时，如100 kPa至200 kPa，随着围压的增加，膨胀土的破坏应力有着很大增幅；而在围压较大时，如300～400 kPa时，随着围压围压级别增加，破坏应力的增幅较小，即在增加相同大小的围压下，随着围压水平的增加，破坏应力的值的增幅在减小，即高围压时候，膨胀土的强度增幅较小。

以轴向应变达12%时，作为试样破坏条件，加载破坏试样外形呈纺锤状，中部发生鼓胀，试样两端有细微裂纹，未见明显破裂面，如图3所示。

图3 三轴加载下试样破坏形态(单位：mm)

通过破坏时膨胀土应力状态绘制总应力摩尔圆与摩尔库伦强度包络线(见图4)，可得总应力强度指标如表3所示。

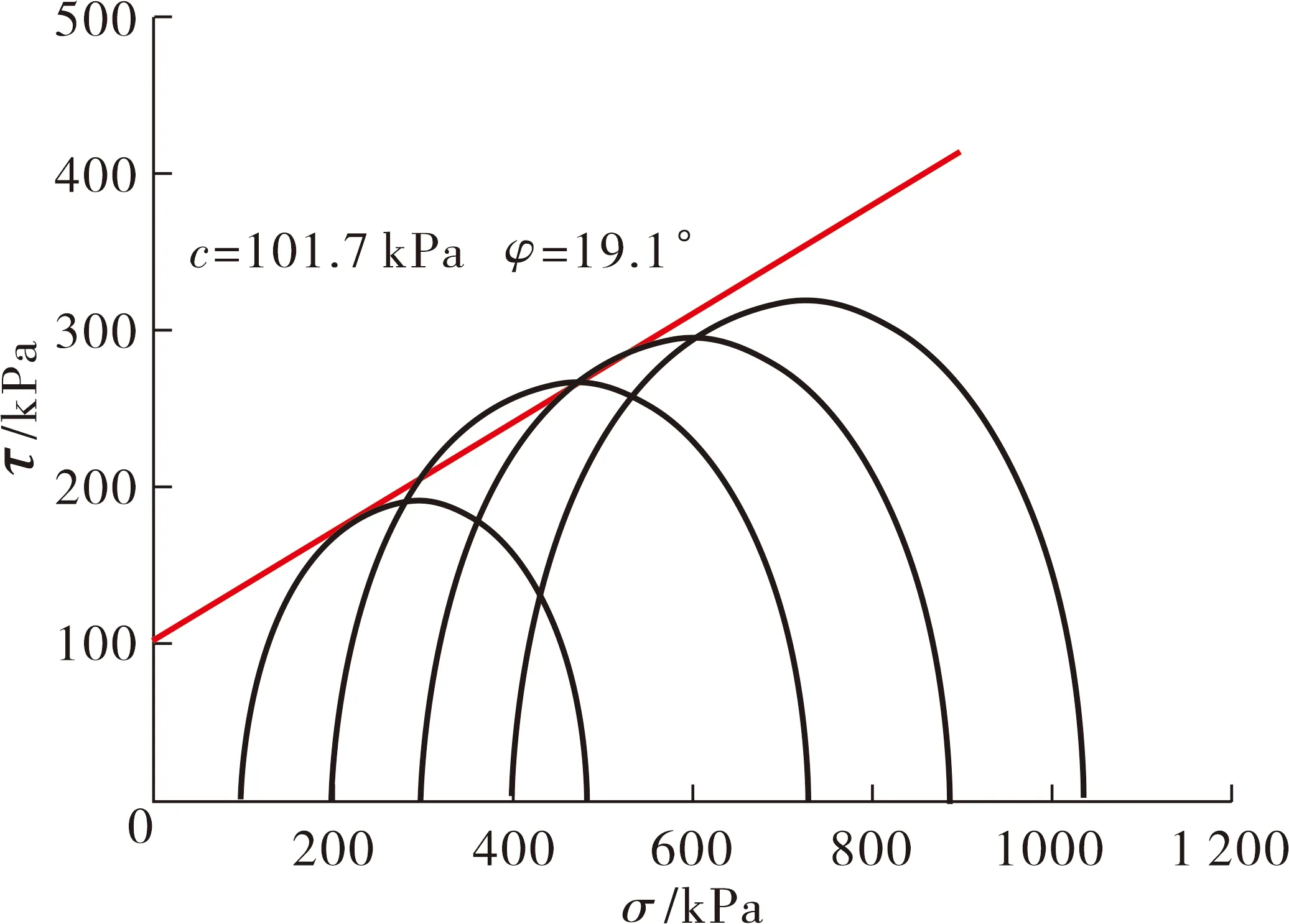
图4 常规加荷总应力强度包络线

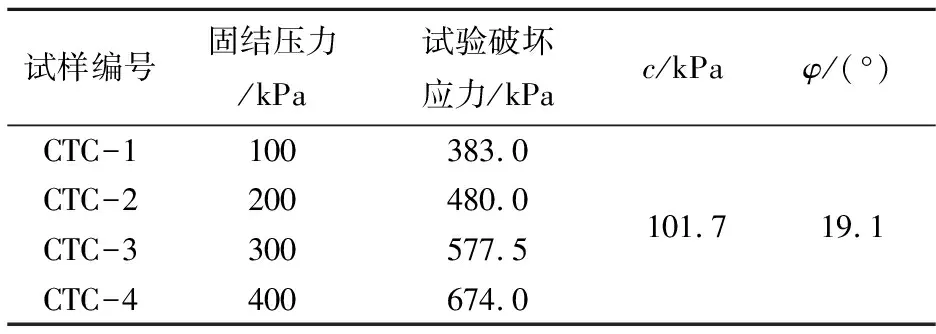
表3 常规加载条件下的强度指标

由强度指标分析发现，合肥膨胀土内摩擦角与一般硬黏土的值相差不大，而其黏聚力远高于一般黏性土平均水平，究其原因在于合肥膨胀土高密实度，以及天然状况下所处的15%含水率，使得孔隙率较小，孔隙中自由水少，孔隙水主要以结合水形态存在，使得剪切过程中黏粒间粘结作用强。

2.2 应力-应变曲线归一化

在不同的围压、含水率、扰动性、应力路径条件下，同一类型的土也会呈现出复杂的应力应变关系。为了使用一个统一的理论公式来描述土的应力-应变特性，实现应力-应变关系的归一化，国内外许多学者对此进行了大量的研究。研究表明，应变硬化型土的应力-应变具有归一化特性，即将土在不同的影响条件下的应力-应变曲线，通过某一归一化因子使之归一化在一条直线上。

常规三轴试验的结果来看，膨胀土为塑性破坏型，其应力应变关系表现出非线性的特点，具有复杂的力学特性。为进一步探究膨胀土常规加载作用下变形特征，采用应力-应变归一化方法对合肥地区典型膨胀土开展归一化分析。

根据膨胀土应力应变双曲线硬化特征，选用Kondner双曲线模型进行拟合，即

(1)

式中：σ1为轴向应力；σ3为径向应力；a-1为初始切线值；b-1为双曲线渐进值。

由双曲线方程的几何关系可知，参数a是初始切线模量Ei的倒数，即

(2)

b是应力-应变曲线渐近线的倒数，即

(3)

对式(1)进行处理，公式两边同乘系数N，得到式(4)，即

(4)

由式(2)～(3)可得到

(5)

(6)

(7)

式中：N为所取的归一化因子；an和bn分别为经过归一化处理的归一化系数，均为常数。

以Kondner双曲线模型公式为基础进行的归一化处理，选取的归一化因子需要满足式(5)～(6)的要求，即归一化条件。土的归一化特性研究中，采用的归一化因子通常有围压、固结压力(K0固结时取平均固结压力)、偏应力渐进值和初始切线模量等。初始切线模量和极限偏应力是使用较多的归一化因子。对于一般土体的应力-应变关系，归一化效果通常较好，但是其包含的物理意义单一。

摩尔-库伦模型是土力学的经典本构模型，参数少且易获得，并能反应土体的摩擦特性。基于摩尔-库伦强度准则可知，在达到土体的破坏条件时，应满足

(8)

式中：σ1为大主应力；σ3为小主应力；c为内聚力；j为内摩擦角。

大主应力σ1和小主应力σ3满足

(9)

将式(9)代入式(8)中，峰值强度即破坏应力可以用土的内摩擦角和土的内聚力表示为

(10)

由图4可知：破坏强度(σ1-σ3)f与围压σ3有关，不同的σ3有不同的破坏强度。将表3中的抗剪强度指标带入上式，得到在不同固结压力下的破坏强度，见表4。取其破坏强度(σ1-σ3)f作为归一化因子，进行归一化处理，如图5所示。

表4 不同固结压力下的归一化因子取值

图5 归一化的应力-应变曲线

从固结应力与破坏应力的数值关系上可以看出，固结应力与破坏应力对合肥地区膨胀土的应力应变归一化性状是存在密切联系的。根据前文对于不同固结压力对于膨胀土应力应变关系曲线的影响探究，从微观上可以解释为固结压力的大小影响了土体内部颗粒紧实程度，并反应在土体最终破坏应力的大小上。

采用破坏应力作为归一化因子进行归一化处理后应力与应变满足式(11)～(12)描述的关系，即

(11)

(12)

将图5中数据进行变换处理，见图6。

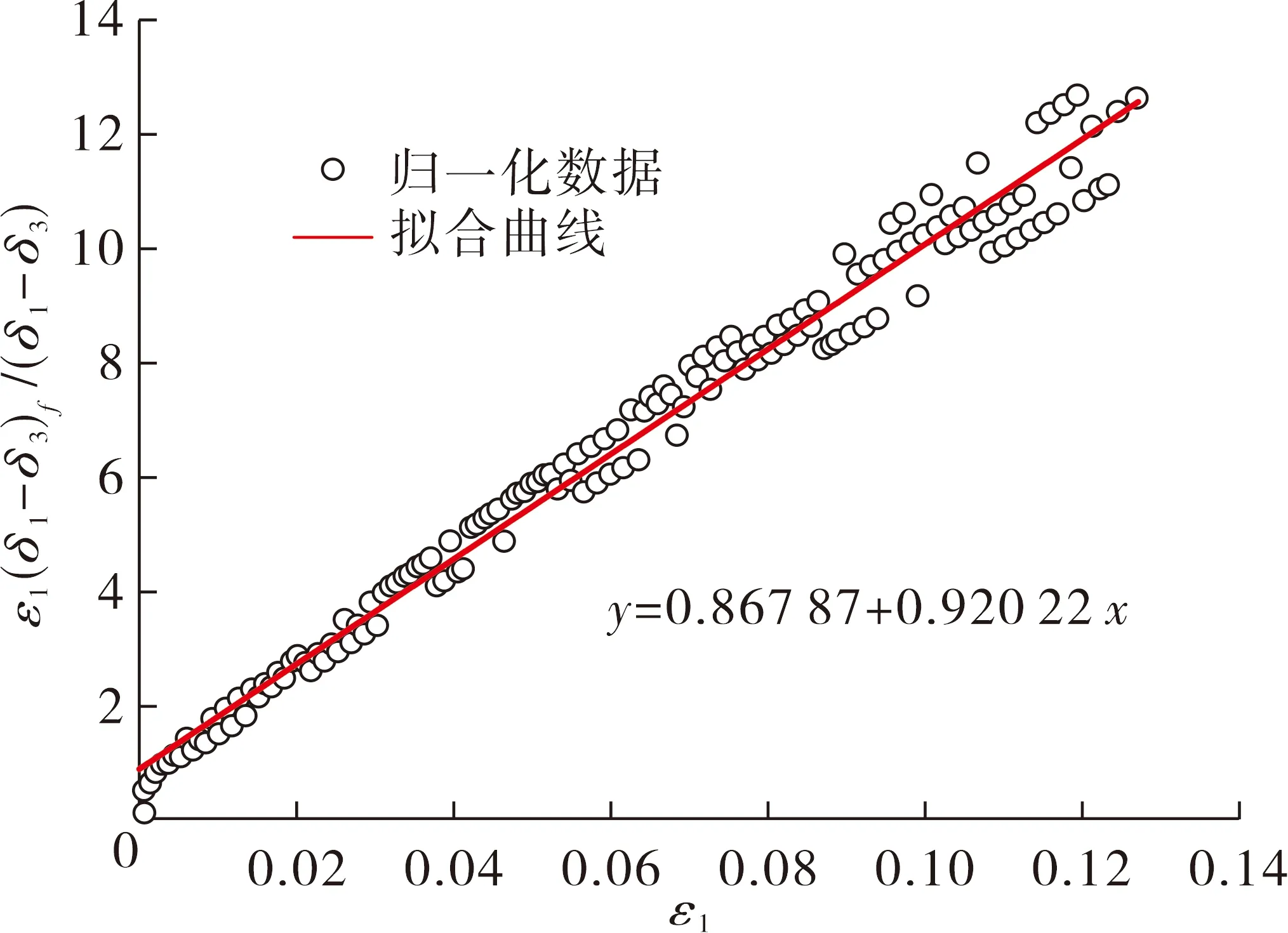
图6 坐标变化下归一化数据线性拟合

将图中数据点进行线性拟合，确定归一化处理后的系数，拟合方程为

y=0.920 22x+0.867 87.

(13)

归一化处理后的系数an和bn中，an=0.867 87，bn=0.920 22，拟合相关系数R2=0.983 3，为高度相关。

用归一化公式中的系数除以破坏应力，反求系数a*和b*，并与原各围压等级下系数对比，见表5。可以看出，采用破坏强度(σ1-σ3)f作为合肥地区典型膨胀土应力应变归一化因子做归一化处理效果较理想，所建立归一化方程能够很好的反应各级围压下的应力应变关系。

表5 拟合系数对比

3 结论

1)在不同围压下，膨胀土应力-应变关系均表现出典型双曲线应变硬化型特征，其破坏偏应力随初始固结应力增加而增大。

2)加载破坏试样外形呈纺锤状，中部发生鼓胀，试样两端有细微裂纹，无明显破裂面，受膨胀土内部孔隙结合水影响，其内摩擦角与一般硬黏土的值相差不大，而黏聚力远高于一般黏性土平均水平。

3)基于Kondner双曲线模型，采用归一化分析方法，建立了以破坏应力(σ1-σ3)f为归一化因子的膨胀土归一化方程，该归一化方程对合肥地区典型膨胀土常规加载应力应变拟合度达到99%以上，具有显著归一化特性。该方程对膨胀土地区施工建设具有参考价值。