二树的乘积和Zagreb指数
孙晓玲,高玉斌,杜建伟
(中北大学 理学院,山西 太原 030051)
0 引言
拓扑指数是反映有机分子某些结构特征的数学描述符,在药理学、化学等领域都发挥着重要的作用[1-2]。1972年,Gutman和Trinajstić[3]在研究π-电子总能量对分子轨道结构的依赖性时,首次提出了Zagreb指数,包括第一Zagreb指数M1和第二Zagreb指数M2,分别定义如下:

其中dG(u)表示图G中顶点u的度。这两个经典的拓扑指数(M1和M2)在分子的异系统性、ZE-异构性、手性和复杂性等研究中都有着广泛的应用。
2012年,Eliasi等[4]提出了Zagreb指数的一种变形形式——乘积和Zagreb指数(记作Π*1),与 Zagreb指数相比,乘积和Zagreb指数能更好地预测化合物的某些物化性质。它的数学表达式为:
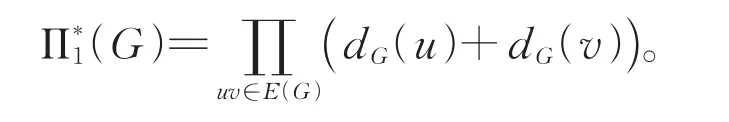
Eliasi等[4]证明了在所有的连通图中,路具有最小的乘积和Zagreb指数,同时还确定了具有第二小乘积和Zagreb指数的树。许克祥和Das[5]刻画了具有最小和最大乘积和Zagreb指数的树、单圈图和双圈图。本文作者[6]最近得到了具有固定割边、割点、点连通度、边连通度的图的最大乘积和Zagreb指数,并刻画了相应的极图。关于乘积和Zagreb指数更多的研究成果可参看文献[7-10]。
下面介绍本文用到的一些定义。设图G=(V(G),E(G))是简单连通图,其中V(G)表示顶点集,E(G)表示边集。我们用NG(v)表示图G中与顶点v相邻的点所构成的集合。G-x表示去掉G中点x及其所关联的边后得到的图。
二树是图论中非常重要的一类图,例如:小世界的Farey图、(伪)分形无标度网络、广义Farey图等都是一些特殊的二树。二树的定义为:最小的二树是2阶完全图;n+1阶二树Gn+1(其中n≥2)是在n阶二树Gn的基础上添加一个新的顶点,且使其与Gn中某条边的两个端点相邻得到的图[11]。
设图Yn是在完全二部图K2,n-2的两个度为n-2的顶点间添加一条边后得到的图(如图1所示)。图Zn是在图Yn-1的基础上添加一个新的顶点,使得该点与Yn-1中的一个2度点以及一个n-2度点分别相邻得到的图(如图1所示)。
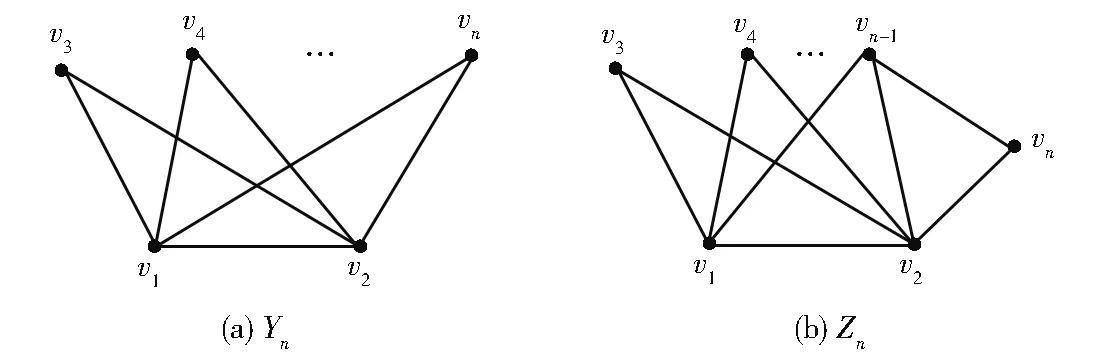
图1 图Yn和ZnFig.1 Graphs of Ynand Zn
文中未加说明的术语和记号可参看文献[12]。
确定不同图类的拓扑指数的极值一直是化学图论的重点和热点研究问题,其结果可以为分析具有极物理或化学性质的化合物的结构提供数学方法和工具。目前,许多图类的乘积和Zagreb指数的极值已经确定(见文献[5-10]),而二树的乘积和Zagreb指数的极值还未得到。因此,本文利用乘积和Zagreb指数的性质,通过数学归纳法和分析结构法,确定了具有最大和第二大乘积和Zagreb指数的二树。
1 主要结论
定理1 设G是n(n≥4)阶二树,则
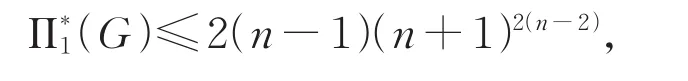
等式成立当且仅当G≅Yn。
证明 我们对n用数学归纳法。当n=4时,G是由4阶完全图删去一条边后得到的图。此时(G)=6×54=2(4-1)(4+1)2×(4-2),结论成立。假设结论对n-1(n≥5)阶二树成立。
在 n阶二树 G 中选取一个 2度点,记为 w。设 NG(w)={u,v},dG(u)=x,dG(v)=y,NG(u){v,w}={u1,u2,…,ux-2},NG(v){u,w}={v1,v2,…,vy-2}。显然 3≤x,y≤n-1。注意到,G-w 是n-1阶二树。因此,由乘积和Zagreb指数的定义以及归纳假设,可得
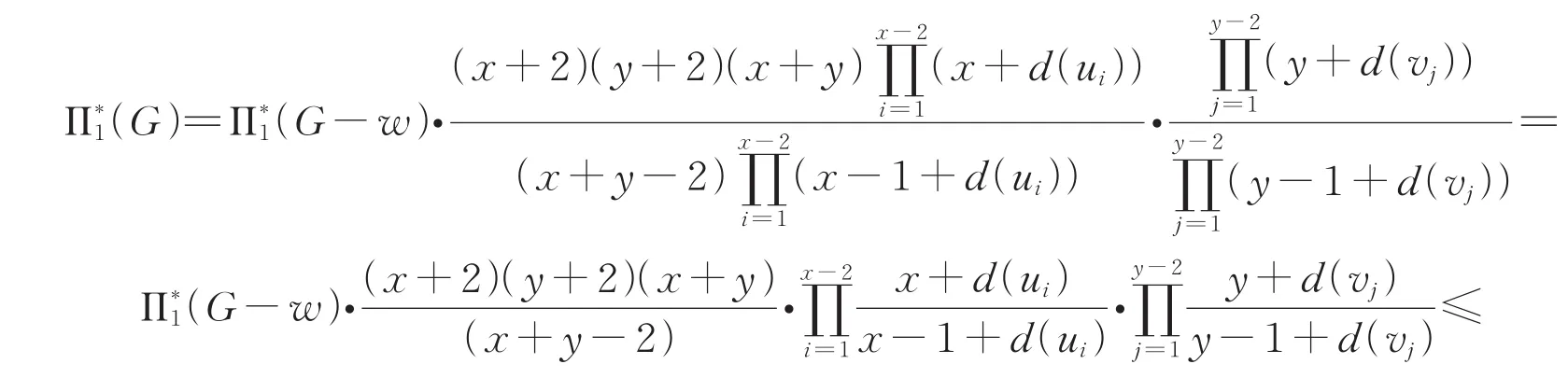


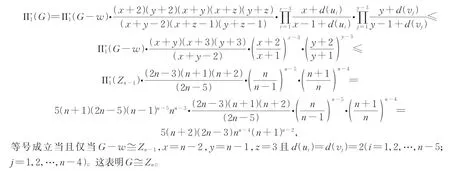
由定理1和定理2,我们确定了具有最大和第二大乘积和Zagreb指数的二树,但是具有最小乘积和Zagreb指数的二树仍然是未知的,下面我们给出公开问题:
问题1 确定n阶二树集合中关于乘积和Zagreb指数的最小极图。

