RHIC-BES能区Au+Au碰撞中粒子横动量的研究

张班，李保春

（山西大学 物理电子工程学院，山西 太原 030006）

0 引言

在相对论性核子以及核碰撞实验中人们可以测量到多种不同粒子。这些粒子的横动量（pT）谱为主要的观测量之一，具有重要的物理意义，因为它揭示了反应系统的激发程度、粒子各向异性等性质。横动量pT的分布范围一般很宽，从0到100 GeV/c以上，与碰撞能量有关。在非常低和非常高的区域中，粒子的pT谱形状可能不同，某些情况下差异可能是非常大的。对于不同的核碰撞系统，在特定碰撞能量下，分析粒子的横动量谱特征，通常需要选择一个适合pT谱的谱函数来提取物理信息，如快度dN/dy、动力学冻结温度T0、平均横向流速βT等，并可以对粒子的特征特性和生成进行讨论。值得注意的是，这其中存在许多不同的函数，有的是由实验数据根据经验拟合给出的，有的是从理论模型推导给出的。应用适合的谱函数进行综合分析，可以获得碰撞系统的相关性质。

物质组成一直是人类探索的重要主题，而相关的基本粒子是极其微小的，探测到并且研究它们的时候需要用到专门的大科学装置——加速器，如：美国的相对论重离子对撞机（简称：RHIC）、欧洲的大型强子对撞机（简称：LHC）［1］。本文中用到的实验数据就是来自RHIC上的STAR探测器。在对撞机上的高能核碰撞实验中，把需要进行碰撞实验的粒子或核加速，直到其能量变得非常大，然后让这些粒子或核进行对撞。在极高温、极高密的核对撞区可发生量子色动力学（QCD）相变，夸克、胶子解禁闭，形成夸克胶子等离子体（QGP）［2-3］系统。该系统会膨胀，逐渐冷却，进入强子化且继续膨胀，并有出射粒子被测量到。不同类型的粒子可能经历不同的演化阶段，进而表现出不同的分布行为。此外，相似高能碰撞过程的不同粒子分布可能有一些相似之处。对于夸克物质来说，当交换胶子的能量很低时，约束和手征对称性得到恢复，因此，夸克和胶子几乎没有质量。当交换胶子的能量非常高时，约束和手征对称性被破坏，这给了夸克静止质量。QGP的特点是人们非常热衷的话题。人们对碰撞过程中粒子的产生机制难以有详细的了解，因此需要利用探测器接收到的末态粒子的特性来反推出高能碰撞的演化过程。对于末态带电粒子，快度谱或赝快度谱（η）和横向动量谱分别反映了相互作用系统的纵向延伸和横向激发的程度。研究各种粒子的横动量谱是研究高能碰撞过程的一种很有前途的方法，从而可以理解QGP的本质。大范围和不同中心度的粒子谱研究是进一步了解QGP强子化和粒子产生机制的重要方法。

RHIC的束流能量扫描（BES）项目是为了更加具体地研究QCD的相图结构［4-6］以及找到QGP的性质。2001年，STAR探测器获得了第一轮实验数据，在2010-2014年，RHIC进行了BES项目第一阶段实验，碰撞能量为7.7 GeV至200 GeV，BES项目第一阶段的研究结果十分有意义，并且人们发现了QGP存在的证据［7］。本文使用了2010年和2011年RHIC BES项目第一阶段STAR实验在每核子对质心能量，11.5，19.6，27和 39 GeV 下 Au+Au碰撞的横动量分布的实验数据［8］。横动量谱被认为是热物质横流的结果。目前文献已经研究了在高横动量下的p+p和Pb+Pb碰撞［9］以及 Au+Au 碰撞［10-11］和 p+Pb［12］碰撞中质子、介子和质子的产生，并且用Boltzmann-Gibbs函数方法分析了A+A碰撞，其中还运用了指数形式［13-15］。此外，在文献［16］中利用非广延分布对BES能区下的单个粒子的横动量分布进行了研究。通过用Boltzmann函数对横动量分布的拟合，并且分析横动量分布对碰撞能量以及碰撞中心度的依赖关系，可以更好地了解各种粒子产生机制与高能碰撞演化过程。

合作组得出的实验数据在理论上可以用不同的方法来拟合，如 Erlang分布［17-18］、Tsallis分布［19-20］、Hagedorn函数［21］等。对于强子横动量谱而言有少数夸克水平上的研究。此外，对于较大的横动量（横动量大于5 GeV/c）的描述一般采用多组分函数来描述。有些宽谱需要双组分函数。作为一种可行的方法，我们希望用一个简单的函数来系统化各种粒子的横动量谱。在本文中用单组分的Boltzmann函数拟合RHIC下BES能区的Au+Au碰撞中产生的各种粒子的横动量谱。通过改变主要参数（包括有效温度T），研究了所考虑的Boltzmann函数的部分特性。通过用Boltzmann函数对横动量分布的拟合，并且分析横动量分布对碰撞能量以及碰撞中心度的依赖关系，可以更好地了解各种粒子产生机制与高能碰撞演化过程。

1 高能碰撞中横动量谱的函数描述

低横动量区由软激发过程贡献，在软激发过程中可以提取动力学冻结温度和横向流速，而硬散射过程对提取动力学冻结温度和横向流速没有贡献或贡献很小。Boltzmann分布函数是用来统计粒子分布规律的，经常应用在微观粒子系统，并且它非常适合用于描述在低横动量范围内产生的粒子谱。高pT谱与强散射过程（pQCD）有关。没有明确的边界来区分软过程硬过程。此分布是以Maxwell气体分子运动理论为基础发展起来的，能够计算特定微观状态在有限温度下的观测概率。在经典理想气体模型中，动量各分量的概率密度函数：

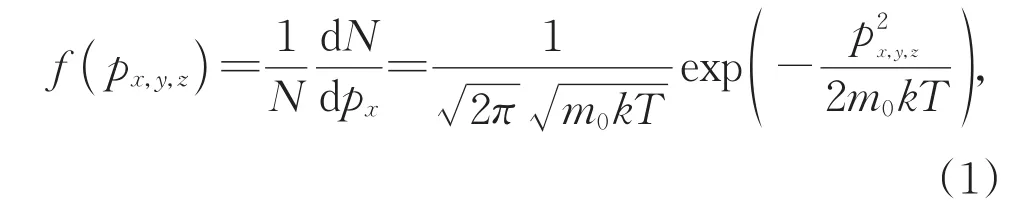
式中，参数T为温度，m0是对应粒子的静止质量，k是Boltzmann常数。粒子动量的分布函数是：

需要说明的是，上述公式中的T是有效温度，其中包含了描述热运动的动力学冻结温度和描述集体运动的横向流速的贡献。一般地，有效温度与动力学冻结温度的增大或减小行为一致，在多数情况下，本文关于有效温度的讨论对动力学冻结温度也适用。

2 数据比较分析

由于探测器在低pT时的接收程度有限，在高pT时的统计量有限，一般合作组在这些区域未得到横动量谱，计算需要外推到这两个区域，以获得较为完整的pT区域以及平均横向质量。对低pT的外推尤其重要，因为它对两个观测值都有显著贡献，而对高pT的外推通常提供的贡献小得多。单组分Boltzmann分布可用于拟合低pT谱，并将其外推到未测量的低pT区域。

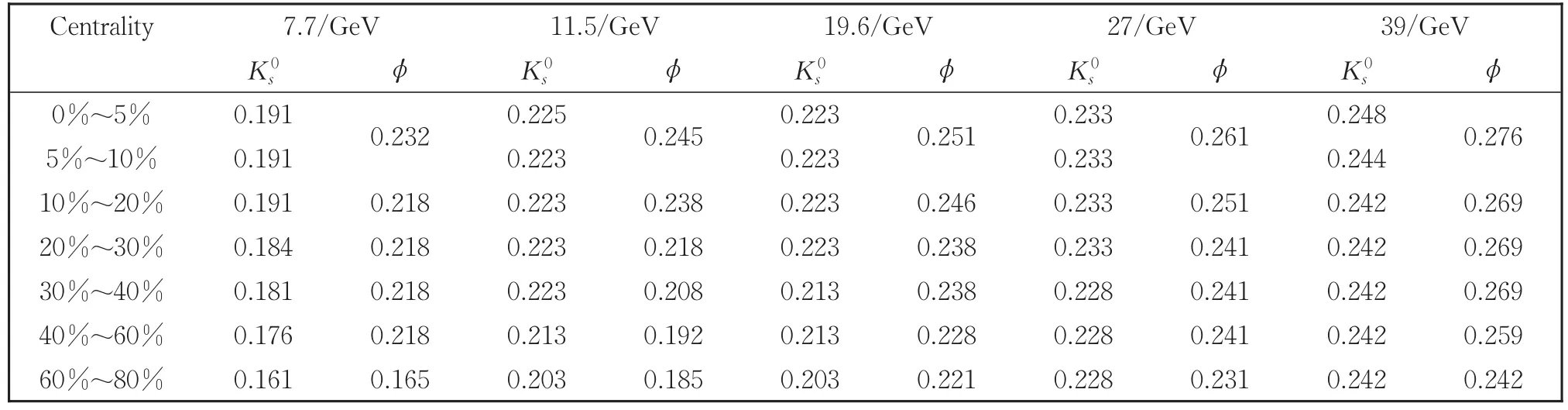
表1 图1中不同碰撞能量下T的值Table 1 Values of T corresponding to the solid curves at different collision energy in Fig.1

图2所示为在束流扫描能区（7.7 GeV～39 GeV）的Au+Au碰撞中，在中快度区|y|＜0.5产生的Λ和粒子在不同中心度下的横动量谱。图中不同的符号表示具有不同中心度的实验数据［21］，来自STAR合作组。曲线是模型拟合结果，与实验数据变化一致。计算得到的有效温度T的值列于表2中。与图1和图2类似，如图3和图4所示，分别为中快度区|y|＜0.5的Au+Au 碰撞中产生的粒子在不同中心度下的横动量谱。图中，计算得到的结果和实验测量得到的数据［21］依然符合得很好。计算得到的有效温度T的值分别列于表3和表4中。

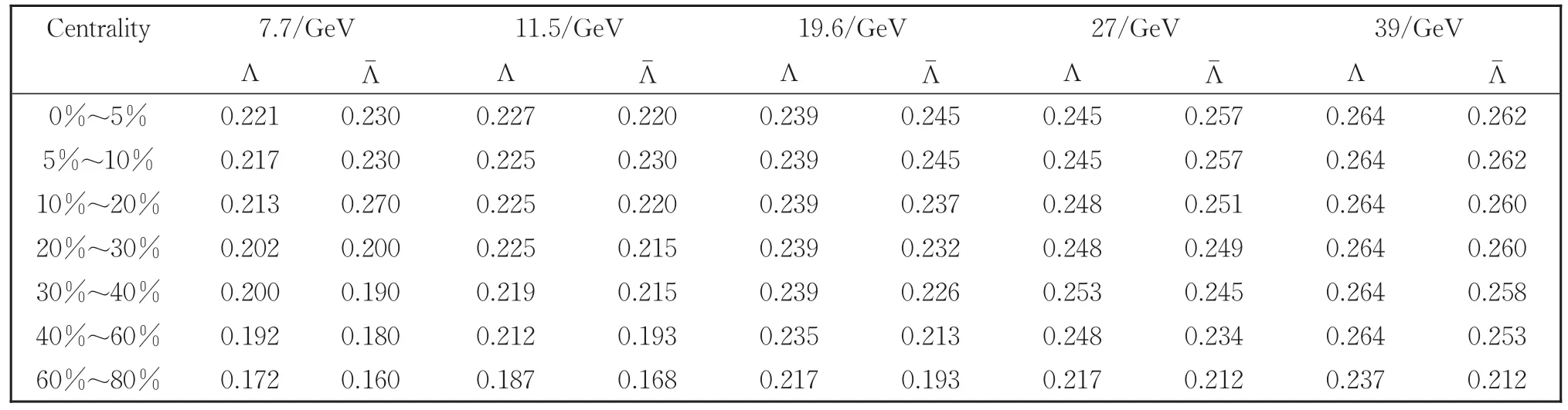
表2 图2中不同碰撞能量下T的值Table 2 Values of T corresponding to the solid curves at different collision energy in Fig.2

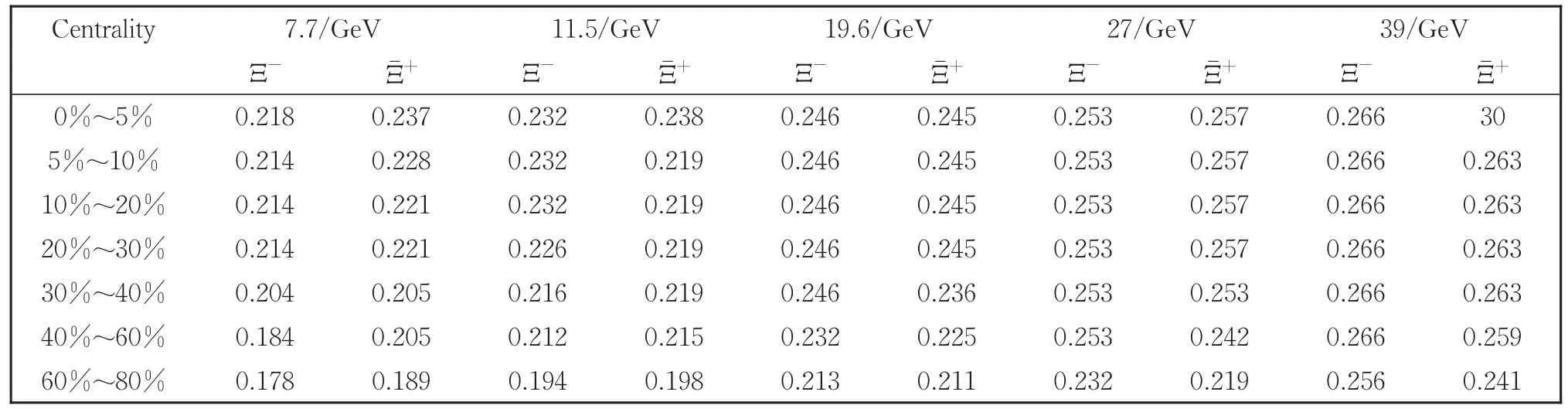
表3 图3中不同碰撞能量下T的值Table 3 Values of T corresponding to the solid curves at different collision energy in Fig.3

表4 图4中不同碰撞能量下T的值Table 4 Values of T corresponding to the solid curves at different collision energy in Fig.4

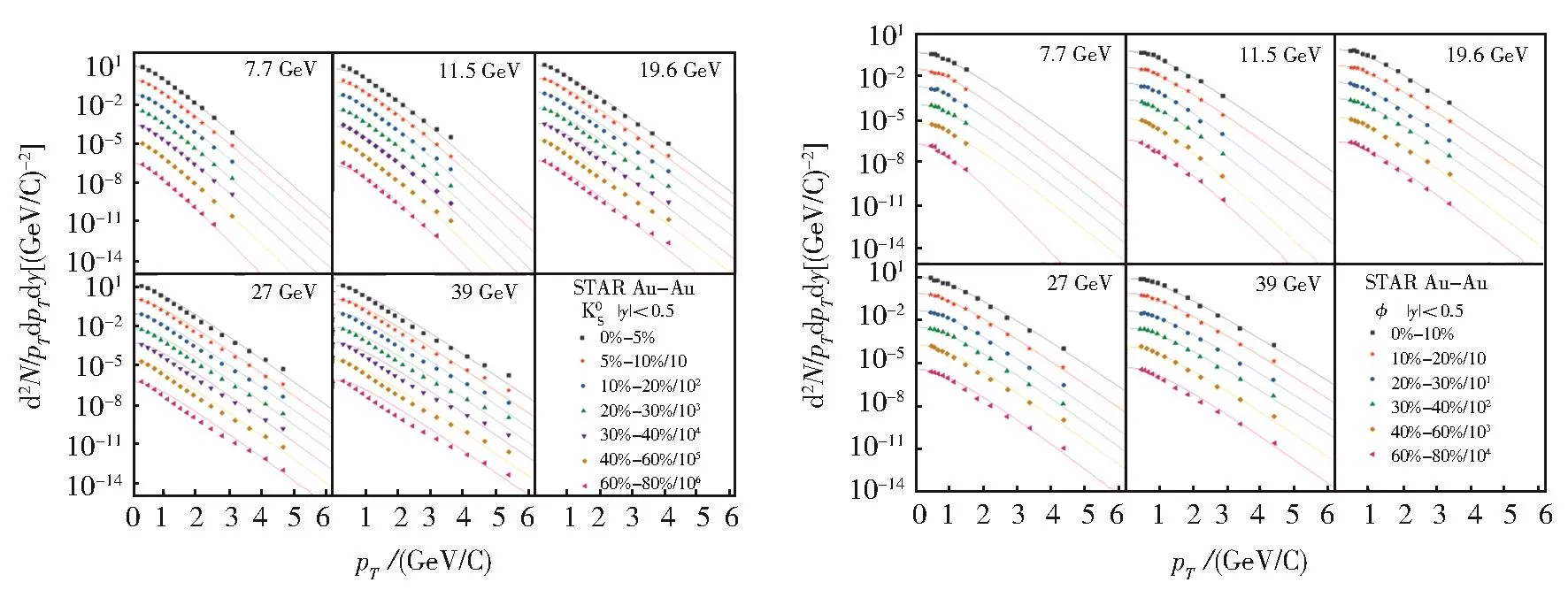
图1 能量=7.7 GeV～39 GeV的不同中心度Au+Au碰撞中的Ks0和ϕ在中快度区（|y|＜0.5）的横动量谱Fig.1 Transverse momentum spectra of mid-rapidity（|y|＜ 0.5）Ks0and ϕ in Au+Au collisions at=7.7-39 GeV energies for different centralities

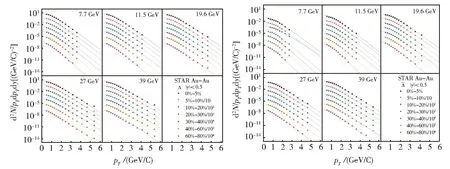
图2 能量=7.7 GeV～39 GeV的不同中心度Au+Au碰撞中的Λ和在中快度区（|y|＜0.5）的横动量谱Fig.2 Transverse momentum spectra of mid-rapidity（|y|＜ 0.5）Λ and in Au+Au collisions at=7.7-39 GeV energies for different centralities

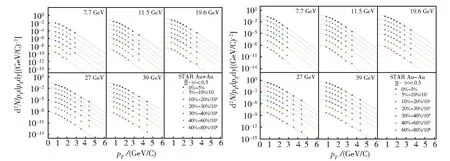
图3 能量=7.7 GeV～39 GeV的不同中心度Au+Au碰撞中的Ξ-和在中快度区（|y|＜0.5）的横动量谱Fig.3 Transverse momentum spectra of mid-rapidity（|y|＜ 0.5）Ξ-and in Au+Au collisions at=7.7-39 GeV energies for different centralities

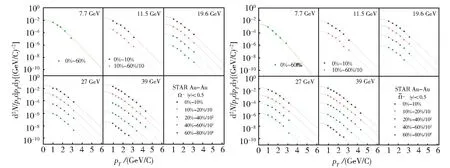
图4 能量=7.7 GeV～39 GeV的不同中心度Au+Au碰撞中的和在中快度区（|y|＜0.5）的横动量谱Fig.4 Transverse momentum spectra of mid-rapidity（|y|＜ 0.5）andin Au+Au collisions at=7.7-39 GeV energies for different centralities

通过图1-4，比较分析了不同能量的Au+Au碰撞中产生的多种粒子的实验数据，可以得到温度参数T相对于中心度C的变化关系，如图5所示。从图中可以看出，在大多数情况下，发射源的温度T随着从边缘碰撞（60%～80%）到中心碰撞（0～5%）的中心度的增加而缓慢增加。这其中的原因是：在中心碰撞中，大量核子参加者参与反应，碰撞剧烈，导致系统的激发程度更高，有效温度和动力学冻结温度也更高［22］。然而，随着中心度的降低和参加者核子数量的减少，碰撞变弱，从而导致相对较低的动力学冻结温度。对于质量相同的粒子和反粒子而言，粒子会比反粒子更早逸出。

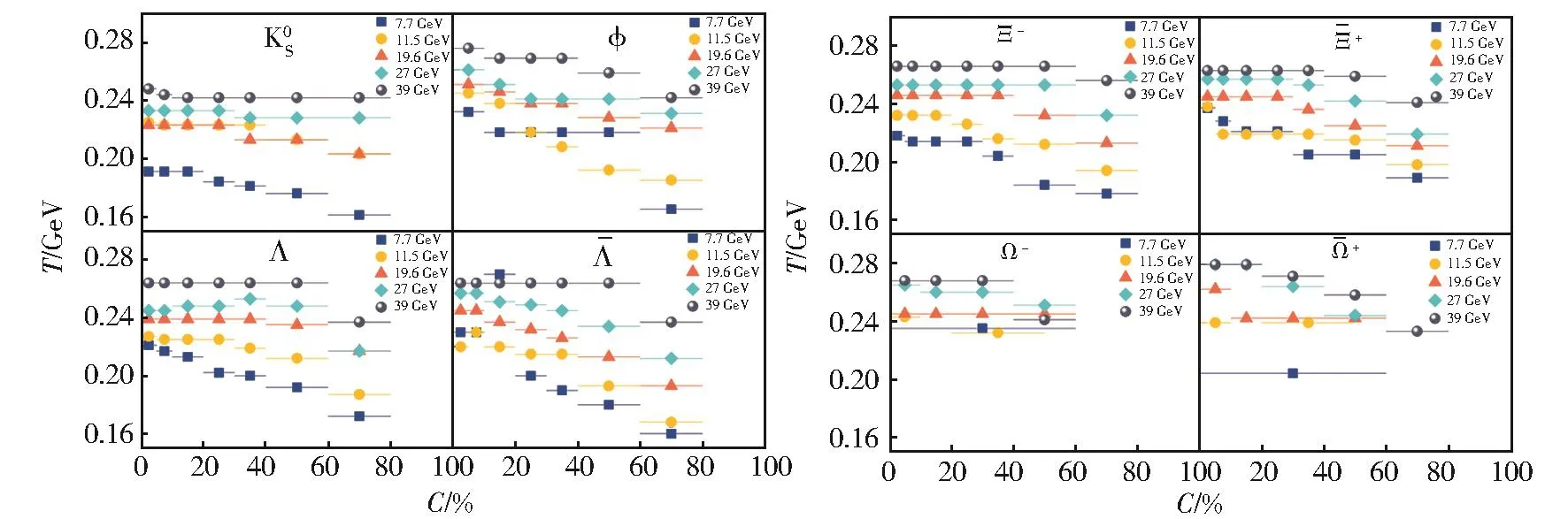
图5 不同能量Au+Au碰撞中各种粒子相应的发射源有效温度与中心度的关系Fig.5 Dependence of effective temperature Ton centrality C for different particles in Au+Au collisions at different energies

图6展示了温度T随着对应粒子静止质量m0的变化趋势，分别给出不同能量Au+Au碰撞所对应的结果。随着碰撞中心度的增加，系统温度升高；能量越小，温度增加越明显。如图所示，温度T与粒子的静止质量m0基本呈正相关。这说明大质量粒子是在较高的温度下产生的。基于理想气体模型的结果与流体力学模型的结果一致。根据流体力学模型的观点，在系统演化并伴随温度降低的过程中，大质量粒子会被先行遗留下来，自然相应较高的发射源温度。可以说，大质量粒子相应的发射源温度高，是因为被遗留了下来，不是因为被激发了出来。

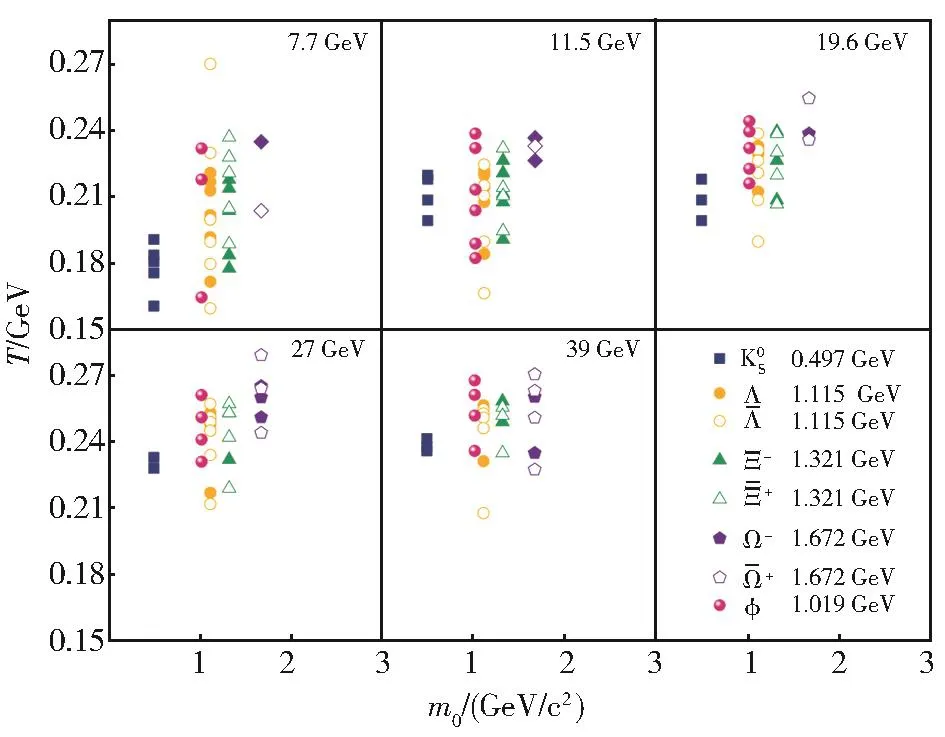
图6 不同能量Au+Au碰撞中各粒子有效温度T与m0和中心度的关系Fig.6 Dependence of effective temperature T on m0for different particles in Au+Au collisions at different energies

3 结论

通过研究高能碰撞的粒子产生及分布［23-24］，可以分析碰撞系统中物质的性质。在本文中，我们研究了在质心能量、11.5、19.6、27和39 GeV下Au+Au碰撞所产生的多种奇异强子和ϕ）在不同中心度下的横动量谱，分析了STAR合作组测量的实验数据。一般来说，STAR测得的BES能区的数据与以前AGS、SPS实验组和RHIC的数据存在较大关联。通过Boltzmann函数的方法描述横动量谱，发现模型结果与实验数据基本一致。在某些情况下，这些拟合定性地反映了数据的变化趋势。从横动量谱的数据对比分析中得到了有效温度T。结果表明：对于Au+Au碰撞，温度T从边缘碰撞到中心碰撞，随着碰撞的中心度的增加而增加。这是由于边缘碰撞中参与核子数的减少，导致系统的激发度降低［25］。与中心碰撞相比，边缘碰撞离平衡态较远，但碰撞仍然接近平衡态。通过横动量谱的对比分析发现：不同粒子对应的发射源有效温度T都会随着它们的静止质量m0的升高而具有不同程度的升高。这表明质量m0较大的粒子产生于更早的时刻，对应的态离平衡态更远，但碰撞系统仍然接近平衡态。本文采用Boltzmann函数分析方法，通过研究不同能量Au+Au碰撞中不同中心度下的多种奇异强子的横动量谱，找到了其中的分布规律，并抽取出了系统所蕴含的热力学信息，可为探讨高能碰撞的粒子产生机制提供参考。