多因素不确定种群模型的性质

高采文，张志强，刘宝亮

（山西大同大学 数学与统计学院，山西 大同 037009）

0 引言

在实践中，为了解和控制种群的数量及分布，预测种群对外界环境变化的反映，需要建立体现种群动态变化的系统。1798年英国人口学家Malthus首次建立了Malthus种群模型，他指出人口或种群的数量通常以指数方式增长。连续的 Malthus种群模型［1］为：

其中Nt表示时刻t种群的数量或密度，b和d为实数，分别表示该种群的出生率和死亡率。记r=b-d，定义为种群的内禀增长率。上述模型可整理为：

对于给定的初值N0，该模型的解为：

这是一个确定性模型，对种群数量增长的描述比较笼统，在很多情况下，不能很好地拟合观测数据，而且它忽略了其他内外因素随时间波动对系统行为的影响，所以很难精准预测种群的变化趋势。比如，如果种群的内禀增长率r大于0，种群就一直生存不会灭绝，这是不切实际的。

有学者把种群数量随时间变化看成是一个随机过程，给种群的内禀增长率r加随机扰动，即令r→r+“随机噪声”，得到用随机微分方程刻画的随机Malthus种群模型为：

其中σ是刻画噪声强度的常数，W(t)是白噪声或均值为0的高斯噪声。对于给定的初值N0，模型的解可表示为：

近年来，还有学者把随机模型加以推广，得到多因素随机种群模型。例如文献［2］研究了两种随机因子对种群灭绝的影响：

其中We(t)表示环境波动产生的随机性，Wd(t)表示统计产生的随机性，σe表示环境波动的强度。随后，文献［3］又推广到两个斑块下的随机种群模型：

其 中 i=1，2，j=1，2，i≠j，D是扩散率 。 这 些多因素随机微分方程模型考虑了多个随机因子同时扰动对种群动态行为的影响。

不确定理论是刘宝碇[4]于2007年提出的，它是建立信度模型的一个数学分支。不同于随机微分方程由Wiener过程驱动，不确定微分方程由不确定过程驱动。其中Liu过程是具有Lipschitz连续样本轨道的平稳独立增量过程，在不确定分析中起着基础性的作用。近几年，不确定微分方程已经成为处理动态不确定系统的主要工具，研究者们取得了丰硕的成果。Yao[5]讨论了不确定微分方程解的极值和积分。Ge和Zhu[6]研究了倒向不确定微分方程。Lio和Liu[7]提出了不确定微分方程中时变参数的矩估计法。Yao等[8]给出了不确定微分方程依均值稳定的概念。Sheng和Gao[9]讨论了一类线性不确定微分方程指数稳定的充要条件。Yao[10]研究了带跳的不确定微分方程。Zhu[11]提出了不确定分数阶微分方程，并将其应用到利率问题的研究中。Li等[12]研究了一类多因素不确定微分方程。Zhang等[13]对多因素不确定微分方程的稳定性进行了探讨。不确定理论已经广泛应用在不确定规划、不确定可靠性分析、不确定金融等领域。在实际中，出生率和死亡率都具有不确定性，所以在不确定理论框架下研究种群动态系统的性质有重要意义。基于此，本文研究了出生率和死亡率用两个不同的不确定变量来刻画的多因素不确定种群模型。

1 模型的建立

现有种群模型的研究大多是对确定性模型和随机模型的讨论与分析。而实际情况是生物种群的数量变化受到各种不确定因素的共同作用。比如，内部因素中生物种群的内部竞争、自然出生率和死亡率等，具有一定的不确定性。外部因素如环境变换、季节更替和人为干扰、突发疫情等，也具有一定的不确定性。在自然界中，不受不确定噪声干扰的生物种群几乎是不存在的，理想状态下的确定性模型很难反映出真实的种群数量变化规律。因此，不确定扰动开始逐渐被应用于生物种群模型的研究中，大量数据也表明不确定种群模型确实更符合生物种群变化的趋势。关于不确定种群模型的研究目前并不多，文献［14］于2017年提出一个涉及种群年龄结构的不确定偏微分方程模型。文献［15］于2020年提出在内禀增长率上加不确定扰动，即：r→r+“不确定噪声”，得到不确定种群模型：

其中 C1t，C2t为独立的 Liu 过程，σ1，σ2为实数，分别表示两个不确定扰动的强度，由此得出多因素不确定种群模型为：

这是一个用多因素不确定微分方程刻画的种群模型，出生率和死亡率分别受到两个相互独立Liu过程的扰动。在自然界中，不受不确定噪声干扰的生物种群几乎是不存在的。模型（10）考虑了实际存在的不确定扰动，利用多因素不确定微分方程对种群数量进行建模，更符合生物种群变化的趋势，能够更为准确、有效的反映生物种群的动态行为。下面讨论模型的解及α轨道，可以证明以下几个结论。

定理 1 令 r，σ1，σ2为实数，C1t，C2t为独立的Liu过程，多因素不确定种群模型（10）对于给定的初值N0，它的解可表示为：

2 解的极值和积分

在实际中，为了维持社会稳定或生态平衡，当种群数量接近极值时，政府需要制定相应的政策来限制种群数量的自然增长或减少，防止极端现象造成的巨大破坏。在本节，我们给出解的极值的不确定分布。

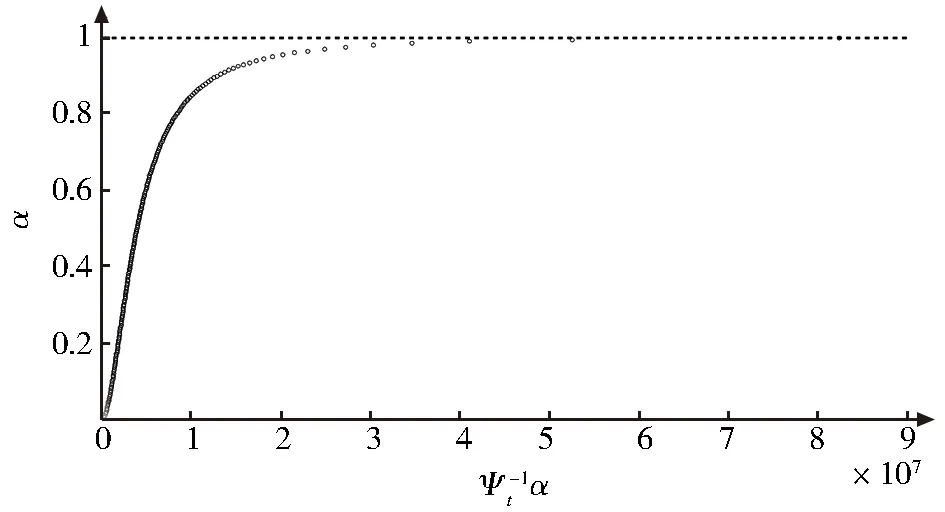
图1 解的逆不确定分布Fig.1 Inverse uncertainty distribution of the solution

图2 解的极值的逆不确定分布Fig.2 Inverse uncertainty distributions of extreme values of the solution

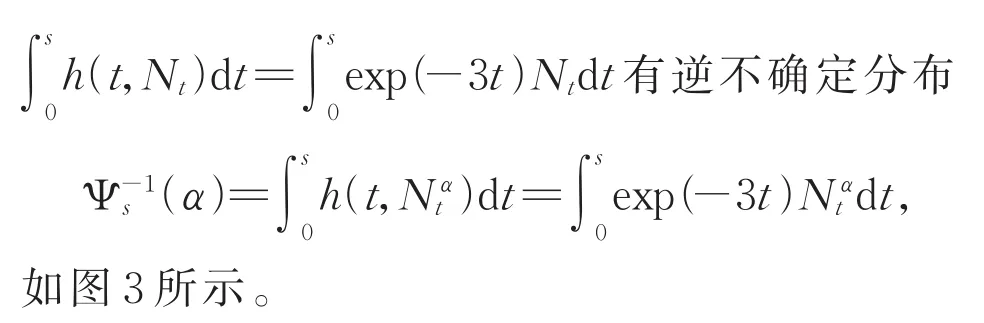
图3 解的积分的逆不确定分布Fig.3 Inverse uncertainty distribution of time integral of the solution

3 模型的稳定性

本节考虑用多因素不确定微分方程建立的动态模型的稳定性。假使模型是不稳定的，初始条件的微小变化将导致解的性态随时间t趋于∞而产生显著的差异。实际生活中，初始状态不可避免的出现误差和干扰，只能近似的确定，所以只有稳定的状态或过程才有现实意义。下面，讨论多因素不确定种群模型在有限时间内的依测度稳定性和依均值稳定性。

3.1 依测度稳定

文献［13］给出了多因素不确定微分方程在t≥0时依测度稳定的定义。根据定义，可以证明多因素不确定种群模型（10）在t≥0时依测度不稳定。然而，在实际中，模型很多情况下应用在t为有限数时，因此下面给出有限时间内多因素不确定微分方程依测度稳定的定义。

3.2 依均值稳定

文献［13］还给出了多因素不确定微分方程当t≥0时依均值稳定的定义。根据定义，可以得到多因素不确定种群模型（10）在t≥0时依均值不稳定。下面给出有限区间[0，T]上多因素不确定微分方程依均值稳定的定义。

4 结论

本文提出由多因素不确定微分方程刻画的多因素不确定种群模型。在自然界中，不受不确定噪声干扰的生物种群几乎是不存在的，给出生率和死亡率分别加上一个不确定扰动来刻画比用其他方式更为准确。文中得出模型的解和α轨道，并分别讨论了解的逆不确定分布、解的极值的逆不确定分布以及解的积分的逆不确定分布。最后研究了有限时间内模型的稳定性，其中包括依测度稳定和依均值稳定。由此得出，考虑多个不确定扰动的多因素不确定种群模型更符合生物种群变化的趋势，能够更为准确、有效的对生物种群进行预测和调控，维护生态系统的平衡。