多边类型LDPC码的构造及其在多维协调中的应用
杨申申,白增亮
(1.山西师范大学 物理与信息工程学院,山西 太原 030031;2.山西财经大学 信息学院,山西 太原 030006)
0 引言
当今时代是一个高度信息化的时代,信息安全的重要性随之也愈发显著。量子密钥分发(Quantum Key Distribution)[1-2]的诞生能够很好地满足对信息加密的需求,它可以使合法通信双方共享一组信息理论上无条件安全的密钥。连续变量量子密钥分发(Continues-Variable QKD,CV-QKD)[3-5]作为 QKD 技术的一个重要分支,具有光源易于制备,探测效率高,中短距离上成码率高,与现有标准光通信组件兼容性好等优点。自1999年被提出后[6],取得了飞速的进展,在实验方面,系统的传输距离和密钥率不断增加,安全性逐步提高,点对点传输最远距离达到202.81 km[7],利用信道复用技术密钥率最高可以达到172.6 Mbit/s[8],基于光纤测量设备无关的演示实验也得以实现[9],并逐渐走向集成化[10]、实用化[11]。
CV-QKD实验技术的不断突破对数据协调的要求也愈来愈高。Leverrier等提出了适用于低信噪比(0.01~1)的多维协调方案[12],能够使得CV-QKD系统的传输距离更远。Jouguet等将多边类型低密度奇偶校验(Multi-Edge Type Low-Density Parity-Check,MET-LDPC)码应用到多维协调当中[13],当码率为0.02,信噪比为0.029时,协调效率为96.9%。Jouguet等利用多维协调结合MET-LDPC码的方案,成功将CVQKD的传输距离扩展到80 km[14],由此获得了研究人员的广泛关注。Wang等实现了0.02,0.05和0.1三个码率下的多维协调,信噪比分别为 0.029,0.075,0.16,效率分别为 96.99%,95.84%,93.40%,并利用GPU的并行计算能力提高了计算速度[15];同年,Milicevic等将码率为0.02时的协调效率提高到99%[16]。Li等利用GPU进一步提高了计算速度[17]。Mani等构造了译码性能更好的MET-LDPC码[18],并对码率0.02进行了分析,协调效率可以达到98.8%。
上述研究工作主要针对码率0.02展开研究,该码率的纠错码可以支持CV-QKD进行百公里以上的密钥分发。当CV-QKD系统工作在中短距离时,有必要对码率0.1展开进一步的研究,且现有研究成果中构造的校验矩阵码长过长,导致计算量过大,计算耗时较长,严重制约了多维协调在实际场景中的应用。本文改进了校验矩阵构造方法,结合随机构造算法和准循环扩展算法构造了一组码率为0.1的MET-LDPC码,基矩阵码长分别为1×103,1×104,2×104,分别扩展到1×105,2×105,5×105,1×106,探究了不同的基矩阵大小和准循环扩展因子对多维协调性能的影响。仿真结果表明,选择码长103的基矩阵并扩展500倍构造出来的校验矩阵纠错性能最佳,当信噪比为0.16时,协调效率为93.4%,帧错误率低至6.8%,译码平均迭代次数为49.99,这几项参数表明我们的方案可以满足系统在中短距离下对数据协调的需求。
1 MET-LDPC码及其构造
Richardson和Urbanke提出了MET-LDPC码[19]。通过在码的设计中引入新的约束条件,使得该码兼具以下优点:(1)在高斯噪声信道上表现出更好的纠错性能;(2)低码率下纠错性能相比于其他纠错码更接近香农极限,在非常低的信噪比下可以降低错误平层;(3)高码率下同样具有非常好的纠错性能。
度分布是分析LDPC码渐进性能的有力工具,MET-LDPC码从节点的角度来定义度分布。矢量d代表边类型的度数;矢量b表示接收信号的信道的参数,该矢量中仅一个变量为1,其余均为0;矢量r表示接收信道的数量。根据这些参数,可以用两个多项式来表征METLDPC码的度分布,分别对应变量节点和校验节点的约束条件,即
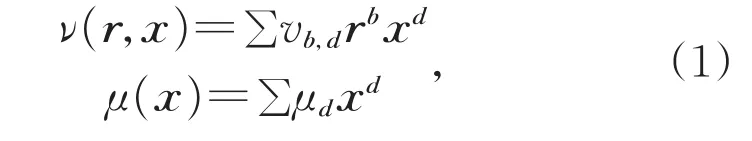
式中系数 νb,d和 μd表示每种节点的比例,均为非负实数。一个度分布对应的码率为

2011年,Jougue等利用密度进化算法寻找出了一组码率为0.02的度分布[13];2017年,Wang等进一步利用密度进化寻找了码率为0.05和 0.10时的度分布[20];2021年,Mani等则利用广义外部消息传递图方法寻找了码率分别为 0.01,0.02,0.05,0.10时的最佳度分布[18],其译码阈值均优于之前的度分布,其中码率0.10的度分布表达式为
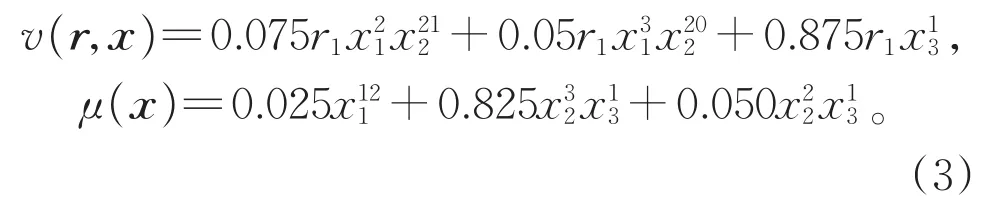
图1所示为该度分布表达式对应的Tanner图。
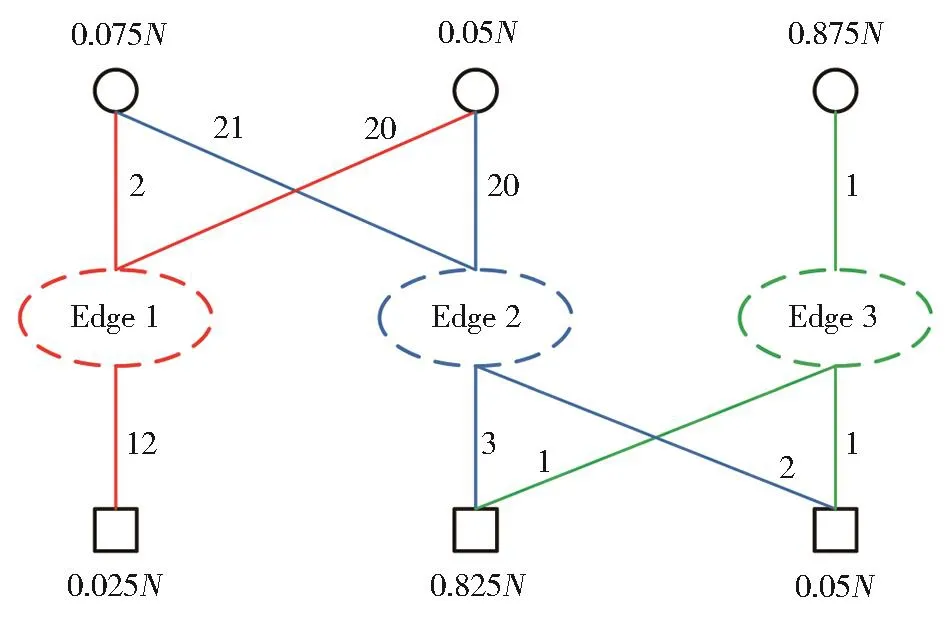
图1 码率为0.1的MET-LDPC码Tanner图Notes:N represents the code length,the circles represent a type of variable nodes,the squares represent a type of check nodes,and the lines between the two types of nodes represent edges.The code include three types of edges,and the numbers represent the number of edgesFig.1 Tanner graph of MET-LDPC codes with code rate 0.1
利用度分布构造校验矩阵的方法可以分为两大类,分别为随机构造和结构化构造。一般来说,随机构造所构造的校验矩阵纠错性能较好,但是当构造尺寸非常大的校验矩阵时,所需时间较长。而且由于MET-LDPC码通常应用在极低信噪比的信道中,校验矩阵的尺寸较大,迭代次数较多,因此译码的延迟时间通常较高,往往需要通过硬件加速的方式来提高计算速度,达到降低延迟时间的目的,准循环结构有利于在硬件中实现并行处理。本文将两种方法结合起来,首先用随机构造算法构造出基矩阵,然后利用准循环算法对基矩阵进行扩展,实现纠错性能和时间复杂度的权衡。
2 多维协调基本原理
CV-QKD系统中传输的信号和量子信道中的噪声均服从高斯分布。当系统的信噪比极低时,发送者Alice的高斯变量方差极小,这就导致大量的信号将集中分布在平均值的附近,叠加一个功率远高于信号的噪声后,接收者Bob接收到的信号将难以进行区分。为了增大高斯信号之间的辨识度,在多维协调方案中对信号进行了多维空间旋转操作,从而将高斯信道传输的高斯信号转化为虚拟二进制高斯信道中传输的二进制信号,有效地增大了信号辨识度。
多维协调方案的具体实现过程如图2所示。对量子态进行测量之后,Alice和Bob共享一组关联的高斯序列X和Y。双方将此高斯序列中每d个元素组成一个向量,标记为X'和Y',然后对每一个d维矢量进行归一化
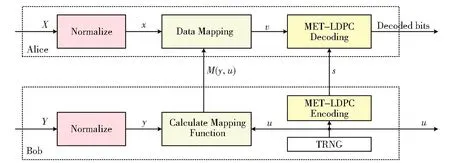
图2 基于MET-LDPC码的多维协调示意图。接收者Bob利用真随机数发生器(True Random Number Generator,TRNG)产生一个比特串,并进行编码,发送者Alice进行译码计算出与Bob一致的比特串Fig.2 Schematic of multidimensional reconciliation based on MET-LDPC codes.The receiver Bob uses the true random number generator(TRNG)to generate a bit string and then encoding.The sender Alice decodes to calculate a bit string that consistent with Bob

式中|X'|和|Y'|表示对向量取模。归一化之后,随机向量被转化为单位球面上的信号点,高斯变量转化为x和y。然后,由接收端利用真随机数发生器产生一组长度与高斯变量相同而且服从均匀分布的随机比特串u,将此随机比特串转换成d维球面矢量
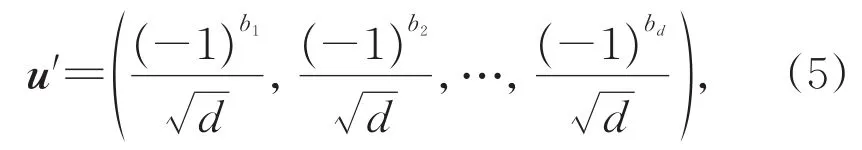
接收端进行d维空间旋转操作,计算出函数M(y',u'),使其满足
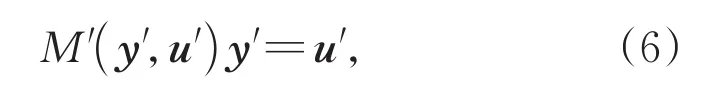
并对u进行编码,生成校验子s,然后将M(y',u')和 s发送给 Alice,Alice 利用接收到的该 函 数 信 息 计 算 M'(y',u')x'=v',最 后 Alice 将计算所得的v作为边信息,通过译码恢复出与Bob完全相同的u。
多维协调的效率可以表示为β=R/C,式中R表示纠错码的码率,C表示信道容量。系统的密钥率K可以表示为
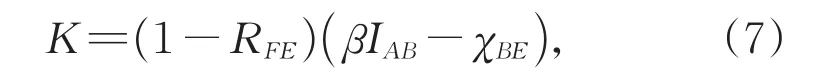
式中RFE表示数据协调的帧错误率,IAB表示通信双方的互信息量,χBE表示逆向协调中可能泄漏给窃听者的信息量。此式表明,帧错误率和协调效率均对系统的密钥率有较大的影响,因此,优化和提升这两项参数是非常必要的。
3 仿真测试结果
相同的度分布下,不同的构造方法、码长等因素均会影响译码性能。为了测试不同校验矩阵的性能,我们首先用随机构造算法构造了码长分别为1×103,1×104,2×104的三种基矩阵,再进行准循环扩展,分别将码长扩展到1×105,2×105,5×105,1×106。对 12 个校验矩阵进行仿真测试后,结果显示译码性能最好的校验矩阵是码长1×103的基矩阵扩展到码长5×105。进一步对该矩阵的性能进行测试,在信噪比为0.155至0.165范围内每间隔0.001测试一组,每组样本总量为100帧,测试所得的译码性能如图3所示。当信噪比小于0.165时,协调效率均能够达到90%以上。
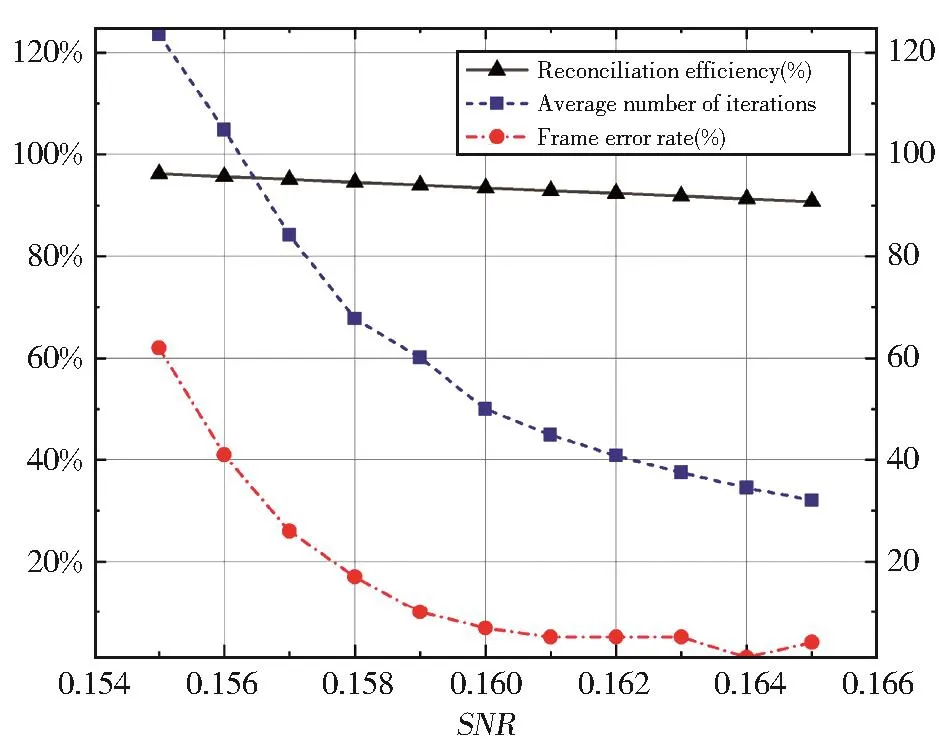
图3 不同信噪比下的译码性能。尽管协调效率随着信噪比的增大而逐渐减小,但帧错误率和平均迭代次数也有所下降Fig.3 Decoding performance under different signal-noise ratios(SNRs).Although the reconciliation efficiency decreases as SNR increases,the frame error rate and the average number of iterations also decrease
为了与前期的两个工作进行对比,对0.160和0.161两个信噪比做了进一步仿真测试,将样本总量扩大到500帧,所得各项参数如表1所示。经过对比可知,本工作的最大优势在于有效地缩短了码长,由于LDPC码的节点数量与码长呈线性关系,缩短码长可以起到降低计算量的作用。由此可知,可以将计算量减少一半。与Wang等工作相比,码长减少了一半,帧错误率相近,由于Wang等没有提供平均迭代次数,所以未能进行对比。与Li等工作相比,平均迭代次数相近,码长和帧错误率均得到显著降低。另外,本文采用随机构造算法来构造校验矩阵,而前期的两个工作均采用渐进边增加(Progressive Edge-Growth,PEG)算法,两者相比,随机构造算法具有原理简单,码长较长时译码性能较好等优点。

表1 与前期他人工作的对比Table 1 Comparison with previous works of others
4 结论与展望
本文构造了码率为0.1的MET-LDPC码,应用到多维协调中表现出良好的性能,当信噪比为0.16时,协调效率为93.4%,帧错误率低至6.8%,译码平均迭代次数为49.99,可以初步满足系统的需求。同时,探究了不同信噪比下,码长、准循环扩展因子等因素对性能的影响,结果表明,构造校验矩阵时基矩阵码长选择1×103且准循环扩展因子选择500时译码性能最佳,该矩阵具有计算量少,能够进行并行计算等优点。下一步,可以利用硬件进行加速,提高协调速度,促进CV-QKD系统在中短距离下走向实用。

