双碳背景下计及新能源大规模接入的电量趋势预测与分析

贺春光，韩 光，赵 阳，宋 楠

（1.国网河北省电力有限公司经济技术研究院，河北 石家庄 050000；2.国网河北省电力有限公司，河北石家庄 050000）

0 引言

近年来，随着我国经济社会的快速发展，能源消费也呈现大幅上升的趋势。为了加快推进能源的绿色低碳转型，积极参与全球气候治理，我国在2020年第75届联合国大会上正式提出了“碳达峰”和“碳中和”的碳减排两阶段目标[1]。2020年，我国全社会碳排放约106亿t，其中电力行业排放约占44%，因此，实现双碳目标，电力行业是尤其重要的一环。在双碳背景下，传统的电力系统将迎来全面的转型升级，新型电力系统在满足经济社会发展需求的前提下，承载了实现“碳达峰”、“碳中和”以及最大化消纳新能源的任务。以智能电网为枢纽平台，以“源-网-荷-储”互动与多能互补为支撑，是具有清洁低碳、安全可控、灵活高效、智能友好、开放互动基本特征的电力系统[2]。在新型电力系统的发电侧，风电、光伏等清洁能源发电的大规模接入，将增加电网调峰、调频的压力。新能源发电所具有的波动性、间歇性和不可预测性，也给电力系统的电量预测带来一定的困难[3]，[4]。电力供应与需求之间处于动态平衡过程，当供大于求时，会造成电力过剩，从而导致弃风、弃光现象严重。因此，在各个不同区域，根据电网对风电、光伏的接纳能力选择新能源的并网方案，离不开准确的电量预测。对电量的准确预测可以为电网的规划建设、优化调度以及负荷的最优分配提供可靠的依据[5]。

随着新型电力系统消费终端电气化水平的不断提高和新能源电源的不断接入，地区的电量呈现多因素化、不确定性增加和变化复杂等特点。这对地区电量的精准预测提出了挑战。目前，国内外专家学者对电量预测进行了大量的研究，预测方法主要分为传统预测和人工智能预测两大类。传统预测方法包括统计法、时间序列法、回归分析法等[6]～[9]；人工智能预测方法有树集成算法、支持向量机和神经网络算法等[10]～[13]。

文献[6]对地区的月用电量与经济因素进行了研究分析，采用随机森林算法对经济因素和用电量进行针对性建模预测，模型的预测精度有所提升。文献[8]考虑了多种因素对电量的影响，提出了基于K-L信息法和ARIMA误差修正的月度电量预测方法。文献[12]提出了一种灰色系统理论与BP神经网络相结合的地区用电量预测方法。采用灰色关联度分析法筛选出对用电量影响较大的因素，建立了BP神经网络模型，实现地区用电量的预测。文献[13]提出了一种时间卷积网络与图注意力网络相结合的分行业日售电量预测方法，搭建了高维度变量分行业日售电预测模型。

目前，针对大规模新能源接入的电量趋势预测研究较少。较多文献注重于传统电力系统的电量预测，未考虑新能源并网对电量的影响，且影响因素考虑较少，预测精度有待进一步提高。在新的电网背景下，本文面向新型电力系统，综合考虑了大规模新能源接入、外部环境和节假日对地区电量的影响，通过定性和定量分析，探索了影响因素与地区电量之间的相关性。本文建立的Informer电量趋势预测模型，采用了粒子群算法对模型的超参数进行寻优，得到最佳电量趋势预测模型。通过算例分析，验证了所提出模型的有效性和稳定性。

1 地区用电量的影响因素分析

在新型电力系统中，新能源电源不断接入到电网中，对地区的用电量趋势产生不同程度的影响。另外，温度、湿度、风速、天气类型等环境因素对地区的用电量也会产生一定的影响。综合考虑各类因素对地区用电量趋势的影响，可以进一步提升地区电量趋势的预测精度。

1.1 定性分析

（1）新能源接入对用电量的影响

由于风电、光伏受天气因素的影响较大，其出力具有不确定性的特点。根据电网的供需动态平衡关系，地区的电量等于传统电源出力和新能源出力之和[14]。传统电源具有较为平稳的出力特性，但风电、光伏等新能源出力具有较强的波动性，因此地区的电量也会出现较强的波动性、随机性和不可预测性。不同规模的新能源接入电网，将产生不同程度的冲击和波动，新能源接入规模越大，冲击性和波动性越强。为了准确把握当地电力系统的未来电量变化趋势，须考虑不同规模新能源接入对地区电量产生的影响。本文采用渗透比指标来衡量新能源接入对电量的影响。图1为3种不同风电渗透率下的地区日电量曲线。由图1可见，随着新能源渗透率的提升，地区日电量曲线波动性增加。

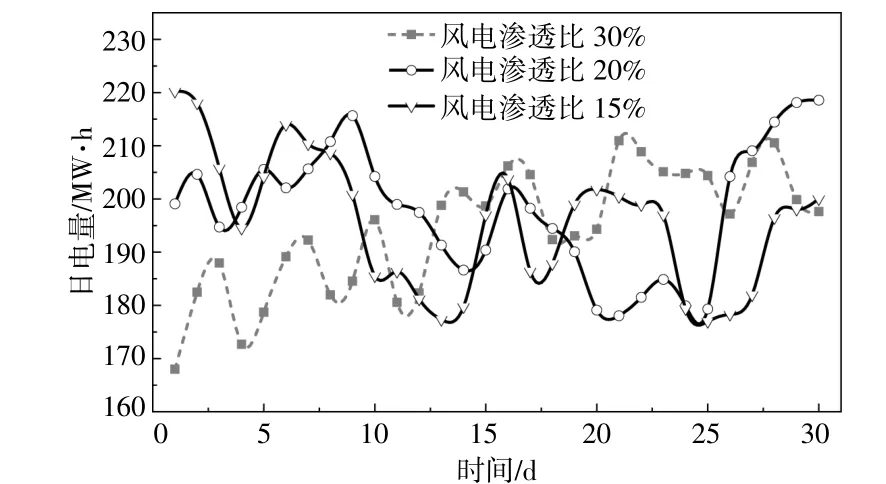
图1 不同新能源发电渗透率下的地区日电量曲线Fig.1 Regional daily electricity consumption curve under different permeability of new energy generation

（2）外部环境因素对用电量的影响

环境温度、湿度、风速、天气类型等外部环境因素对地区用电量也有影响。环境温度的升高将会使电量增加。环境湿度与温度之间呈现负相关关系，因此环境湿度的变化也会导致地区电量的变化。风速的大小直接影响风电的出力，从而对地区电量产生间接性的影响。天气类型有晴天、阴天和雨雪天气等。不同的天气类型会引起地区电量的变化。因此，外部环境因素与地区电量之间存在一定的相关性。图2给出了我国西部某地区2020年日电量与日平均温度的关系。

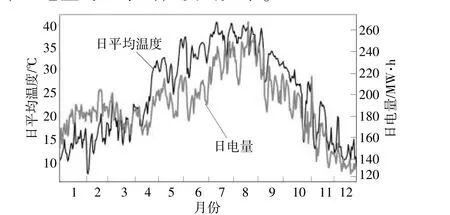
图2 我国西部某地2020年日电量与日平均温度曲线Fig.2 The curve of daily electricity consumption and daily average temperature in a certain area of western China in 2020

（3）节假日对用电量的影响

由于人们在节假日的用电行为发生了改变，因此在节假日期间的地区用电量会发生较大的变化。

1.2 定量分析

采用灰色关联度分析方法对各影响因素变量进行定量分析[15]。通过计算各因素与目标变量之间的关联程度来判断目标变量受因子的影响程度。如果一个因素与目标变量变化的趋势具有一致性，则说明同步变化程度较高，即二者关联程度较高；反之，则二者关联程度较低。因此，灰色关联分析方法是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量影响因素间关联程度的一种方法。

本文以上海市全社会月度电量作为特征因子，首先对初始值进行量纲化处理；然后求出特征因子x0（t）与影响因子xi（t）的差序列Δi（t），进而计算两级最小差值e和最大差值E；再计算关联系数；最后计算关联度。计算公式如下。

通过计算影响因子与地区电量间的灰色关联度，来筛选出对地区电量影响较大的关键因素。表1给出了接入电网风电规模、外部环境、节假日等影响因子与地区电量的关联度。关联度越大，影响因素对地区电量的影响程度越大，反之，影响程度越小。表1中除了湿度因素以外，其他各类因素与地区电量的关联度都在0.5以上，对地区电量变化有着较明显的影响。因此，将历史电量数据、新能源历史出力数据、温度、风速、天气类型以及节假日特征作为决策变量，输入到预测模型中。为了研究新能源出力特性对地区电量造成的影响，引入渗透率指标，将不同渗透率下的新能源出力与电网电量进行关联度计算。从表1可见，渗透率越高，关联度越大，由此说明渗透率越高，对电量变化趋势的影响越大。因此，可将不同新能源渗透率当作不同的场景，对电网电量预测展开研究。

表1 影响因素与电量关联度定量分析Table 1 Quantitative analysis of correlation degree between influencing factors and electricity consumption

2 算法模型

2.1 Informer算法原理

Informer模型的提出为长时间序列预测（Long Sequence Time-series Forecasting，LSTF）问题提供了新的解决方案，能够准确地捕捉输出与输入之间的长期依赖关系[16]。Informer模型是在Transformer模型的基础上提出的一种LSTF模型。与Transformer模型相比，Informer模型具有三大显著的特征：①提出了概率稀疏自注意力机制，在时间复杂度和计算复杂度方面得到了有效的提升；②使用自注意蒸馏技术缩短了每一层的输入序列长度，降低了J个推叠层的内存使用量；③提出了生成式的解码方式，只需一个前向步骤就可以获得长序列输出，避免了预测阶段的累计误差传播。Informer模型保存了Encoder-Decoder的架构，其整体框架如图3所示。

图3 Informer整体框架图Fig.3 Informer framework

（1）Informer模型的输入输出

Informer处理长时间序列过程即稀疏自适应机制算法流程如下。

电量数据、新能源出力数据及气象等因素具有时间序列属性，可以根据历史数据进行预测函数拟合，通过历史观测值预测未来时刻的电量值。对于具有离散特性的节假日因素，可经过独热编码处理变成连续变量。

t时刻的Informer模型输入为Xt={x1t，x2t，…，xLxt|xit∈Rdx}，包括电量历史数据、新能源历史出力数据、气象特征和节假日特征。模型输出为需要预测的序列Yt={y1t，y2t， …，yLxt|yit∈Rdy}， 对于LSTF问题，要求更长的输出序列长度Ly。

（2）稀疏自注意力机制

常规自注意力机制接受3个输入query，key和value，然后使用缩放点积进行计算，即：

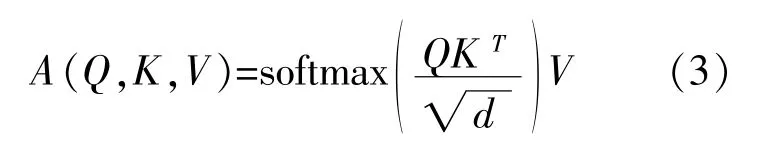
式中：Q∈RLQ×d，K∈RLK×d，V∈RLV×d，Q，K，V分别为输入特征变量经过变换后的矩阵，且具有相同大小；T表示矩阵转置；d为输入的维度；softmax是一种激活函数，它可以将一个数值向量归一化为一个概率分布向量，且各个概率之和为1。

第i个query的注意力被定义为一个概率形式的核平滑方法，即：

自注意机制通过计算p（kj|qi）来将所有的value进行加权求和，这个过程须使用O（LQ，LK）的时间复杂度和内存，这是解决LSTF问题的主要原因。

研究发现，自注意力机制具有潜在的稀疏性，其权重构成了一个长尾分布，部分权重的贡献被忽略。为了度量query的稀疏性，引入了KL散度。

加入一个采样因子c，设定u=clnLQ，使得稀疏自注意力算法仅须为每个query-key lookup计算o（lnLQ）点积，则层layer的内存使用量为O（LKlnLQ）。整体的时间复杂度为O（L，lnL）。

（3）Encoder-Decoder结构

①编码器Encoder

编码器的目标是在内存占用限制内，允许编码器处理更长的序列输入。编码器主要功能是捕获长序列输入之间的长范围依赖，将输入送至多头稀疏自注意力模块。这里采用的是自注意力蒸馏操作，可以减少网络参数，并且随着堆叠层数增加，不断“蒸馏”突出特征。“蒸馏”操作主要为使用一维卷积和最大池化，将上一层的输出送至下一层的多头注意力模块之前，做维度修剪和降低内存占用。蒸馏第j层到第（j+1）层的操作如下式：

式中：[·]AB为多头稀疏注意力机制以及其他必要的操作；Conv1d为在时间维度上执行一维卷积；σ为激活函数，这里采用ELU激活函数；MaxPool为最大池化。

②解码器Decoder

解码器的目标是进行一次前向计算，预测长序列输出。该编码器采用了类似的标准解码器结构，由两个相同的多头注意力层组成。该编码器与标准解码器的区别是，Informer解码器舍弃了动态解码过程而采用了生成式预测，直接地一步输出多步预测结果。该编码器输入格式为

式中：Xttoken为开始字符；X0为占位符；Concat表示将Xtoken和X0合并连接。

最后连接一个全连接层，再到输出层，实现多步预测结果。

2.2 粒子群优化算法

粒子群优化算法（Particle Swarm Optimization，PSO）是一种进化计算技术，其基本思想源于对鸟群捕食行为的研究[17]。粒子群优化算法利用群体中个体信息的共享，使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的可行解。首先给空间中的所有粒子分配初始随机位置和初始随机速度；随后根据每个粒子的速度、问题空间中已知的最优全局位置和已知的最优位置，依次迭代更新每个粒子的位置；最后通过终止条件获得粒子群的最优解。

假设在D维的目标搜索空间中，有m个粒子组成一个群体，其中第i个粒子（i=1，2，…，m）位置表示为Xi=（xi1，xi2，…，xiD）。每个粒子的位置是一个潜在解。通过计算粒子的适应度值来衡量粒子的优劣。粒子个体经历的最好位置记为Pi=（Pi1，Pi2，…，PiD），整个群体所有粒子经历过的最好位置Pg=（Pg1，Pg2，…，PgD），以νi=（νi1，νi2，…，νiD）表示第i个粒子的当前速度。粒子群优化算法采用公式（9），（10）对粒子所在位置不断更新：

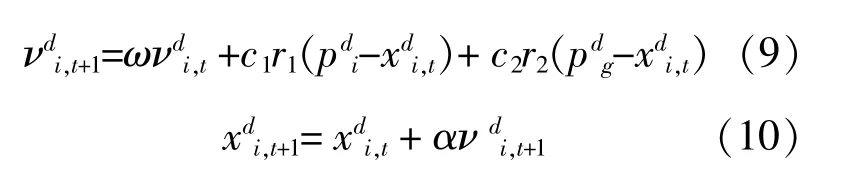
式中：ω为非负数，称为惯性因子；加速常数c1和c2为非负常数；r1和r2为[0，1]内变换的随机数；α为约束因子，目的是控制速度的权重。

当迭代搜索达到最大迭代次数，或到目前为止搜索粒子群的最优位置满足目标函数的最小允许误差时，停止迭代更新，输出粒子群的最优解。

2.3 基于PSO优化的Informer电量趋势预测方法

基于PSO-Informer模型对地区电量趋势进行精准预测。首先通过灰色关联度分析筛选出对地区电量影响较大的因素，将新能源历史出力数据、环境温度、风速、天气类型以及节假日特征作为模型的输入特征集；再对异常值、缺失值、归一化等数据进行预处理。将预处理后的数据集按照8∶2的比例划分为训练集和测试集。训练集用于训练Informer电量预测模型，并通过PSO进行超参数寻优，找到Informer电量预测模型性能最佳的超参数组合。最后使用最优PSO-Informer模型进行电量预测，输出地区电量的预测值。测试集用于评估Informer电量预测模型的效果。基于PSO优化的Informer模型地区电量趋势预测流程图如图4所示。

图4 基于PSO优化的Informer模型地区电量趋势预测流程图Fig.4 Flow chart of regional electric quantity trend prediction based on Informer model optimized by PSO

粒子群算法优化的Informer电量预测算法的具体步骤如下。

步骤1：样本数据预处理。

由于电量预测模型的输入为多维数据，变量之间存在一定的量纲差异，因此在对模型进行训练及寻优之前首先对输入数据进行预处理。通过最大最小值归一化，消除各维度数据之间的量纲。如公式（11）所示，将输入数据转换为[0，1]之间的数。

式中：x为全体样本数据；xmax，xmin分别为样本数据的最大值和最小值。

步骤2：确定Informer的超参数及其搜索范围。

根据Informer的算法原理，确定影响Informer模型的主要超参数，将其作为粒子群优化的搜索空间，并确定超参数的搜索范围。

步骤3：确定粒子群算法的参数搜索空间。

将粒子群中粒子的位置、速度与Informer的超参数相对应，学习因子c1和c2取值为[1，3]。

步骤4：粒子位置与速度初始化。

初始化所有粒子的速度、位置，并将个体的历史最优pbest设为当前位置，群体中最优的个体作为当前的gbest。

步骤5：计算粒子的适应度，获取个体的全局极值与个体极值。

本文采用均方误差作为适应度函数，在每一代的进化中，计算各个粒子的适应度函数值。通过对比各个粒子的适应度值获得个体的全局极值gbest和个体极值pbest。若该粒子当前的适应度函数值好于其历史最优值，那么历史最优将会被当前位置所替代；若该粒子的历史最优好于全局最优，则全局最优将会被该粒子的历史最优所替代。

步骤6：按照式（8），（9）对各个粒子的位置和速度进行更新。

步骤7：完成迭代，输出最优解。

当满足误差要求或者达到设定迭代次数时，停止迭代，输出Informer模型超参数的最优解。若未满足上述条件，则返回步骤5继续进行迭代求解。将进行超参数寻优后的Informer模型作为最终的电量趋势预测模型。

3 算例分析

为了验证本文提出的PSO优化的Informer电量趋势预测模型的有效性，采用我国西部某地区2019年1月1日-2021年12月31日的日电量数据、不同规模风电接入电网的出力数据、天气数据，采集间隔为1 d。将其中80%的数据集作为训练集，20%的数据集作为测试集。

3.1 数据预处理

在模型训练之前，须对原始采集数据集进行数据预处理工作，其中包括异常值与缺失值处理、数据归一化等。在数据采集过程中，由于设备故障、停电等原因造成数据丢失或者异常，这些值的存在会造成数据集不完整而影响到后续的预测工作。因此，采取一定的手段对数据集中出现的缺失或异常值进行处理。当模型的输入数据有多维特征时，维度间数据的量纲是不同的，须对其进行归一化处理，消除量纲不同造成的影响。如式（11）所示，本文采用最大、最小值归一化的方式，将数据集按维度转换到[0，1]之间。

3.2 评价指标

为了验证本文所提电量趋势预测模型的预测效果，须评估模型在测试集上的表现。目前，对于预测领域的评价指标较多，本文主要采用平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、平均绝对百分误差（Mean Absolute Percentage Error，MAPE）等3个评价指标：

式中：yi为真实值；y^i为预测值；n为测试集样本容量。

3.3 确定Informer的最优超参数

采用PSO算法对Informer电量趋势预测模型的超参数进行寻优。研究发现，影响Informer模型性能的超参数主要有batchsize、编码器层数、解码器层数、注意力头数、编码器的输入长度、解码器的输入长度和优化器。将这些超参数作为PSO算法的寻优变量进行求解。经过优化后的最优超参数以及PSO算法的参数初始设置如表2所示。

表2 PSO和Informer算法的参数设置Table 2 Parameter settings of PSO and Informer algorithms

续表2

3.4 实验结果及分析

新能源的大规模接入会影响电量的变化趋势。为了研究新能源发电接入电网对地区电量预测的影响，将其分为两种预测场景：考虑新能源接入的影响和不考虑新能源接入的影响。两种预测场景均采用文章提出的PSO-Informer模型进行验证。前者在构建模型的输入数据时，考虑了新能源出力数据，将其历史出力数据作为重要的输入特征；后者在构建模型的输入数据时，没有考虑新能源出力数据，只是将电量历史数据、天气特征及节假日特征作为模型的输入。图5给出了PSOInformer在考虑和不考虑新能源接入影响时，对地区电量趋势的预测结果。图5显示，考虑新能源接入因素的影响，有利于PSO-Informer模型对电量变化趋势的把握，从而做出准确的预判。

图5 考虑和不考虑新能源接入的PSO-Informer模型电量趋势预测Fig.5 Power trend prediction of PSO-Informer model with and without new energy access

为了进一步细化新能源接入电网对电量预测的影响，设置了15%，20%，30%渗透率下3种不同预测场景，构建了3种不同渗透率下的电量预测模型。通过电量预测结果对比，来具体刻画新能源并网运行对地区电量预测的影响。表3给出了不同渗透率预测场景下，新能源出力对地区电量预测的影响。从表3中可以看出，不同渗透率下，PSO-Informer模型的电量预测效果不同，渗透率越低，预测精度越高。这说明渗透率越高，新能源接入电网对地区电量的影响越大。

表3 不同渗透率预测场景下，PSO-Informer模型对地区电量预测的效果Table 3 Effects of PSO-Informer model on regional electric quantity prediction under different permeability prediction scenarios

为了验证本文提出的PSO优化的Informer地区电量趋势预测方法对电量预测的有效性以及预测精度的提升，使用训练集训练Informer模型，并通过PSO进行超参数寻优，将训练后的电量趋势预测模型在测试集上进行评估和预测。为了突出PSO-Informer模型对地区电量趋势预测的效果，分别采用BP神经网络和支持向量机（SVM）作为对比模型。图6给出了PSO-Informer、BP网络、SVM等3种方法对电量趋势的预测结果。

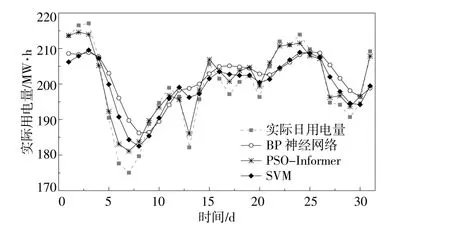
图6 3种模型的电量趋势预测效果图Fig.6 Effect diagram of electric quantity trend prediction of the three models

从图6中可以看出，本文提出的PSOInformer预测方法具有更好的预测效果，在电量趋势发生较大波动时，能够做出有效的预测。BP神经网络模型和SVM模型在电量趋势变化转折处的预测偏差较大，对未来一个月日电量趋势的拟合度不太理想，而Informer模型在电量趋势转折处的预测偏差较小且拟合度较高。通过预测结果对比发现，Informer模型在对长时间序列进行预测时，准确地捕捉输出与输入之间的依赖关系，具有较高的预测精确度。

图7给出了两种对比模型与PSO-Informe模型的预测误差图。由图7可见，BP神经网络模型和SVM模型的日电量趋势预测误差较大，且波动范围较大；PSO-Informer模型的日电量趋势预测误差较小，波动在合理的误差范围内。显然，在长时间预测问题上，PSO-Informer模型优势明显。

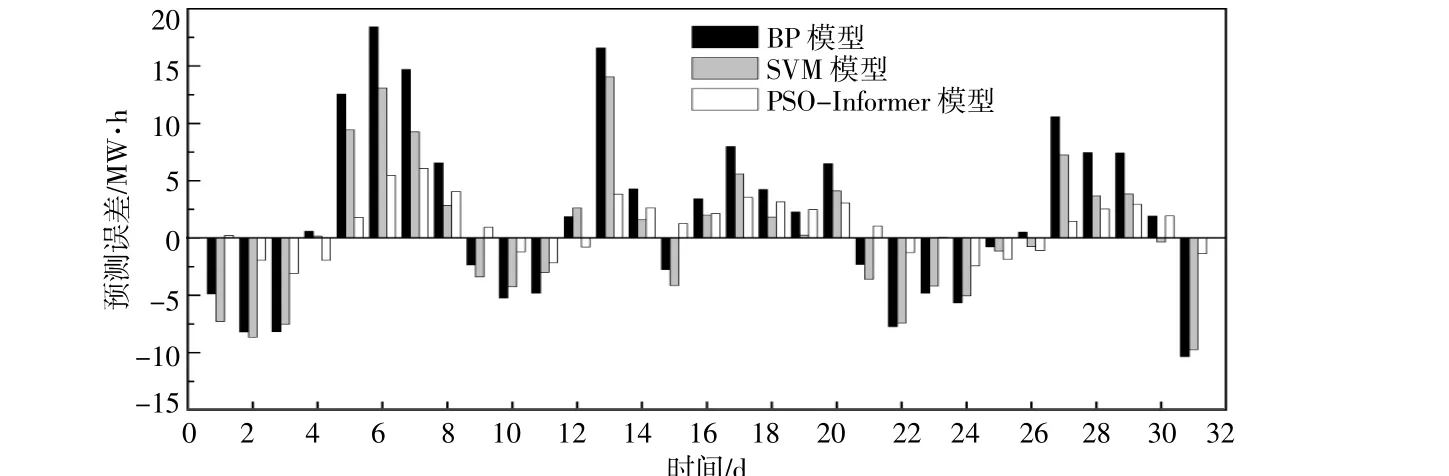
图7 3种模型的电量趋势预测误差图Fig.7 Error chart of electric quantity trend prediction of the three models

表4给出了采用MSE，RMSE和MAPE指标评价3种预测模型在测试集上的表现。从表4中数据可以看出，与另外两种模型相比，本文提出的PSO-Informer模型的3种评价指标值较低，预测误差较小。

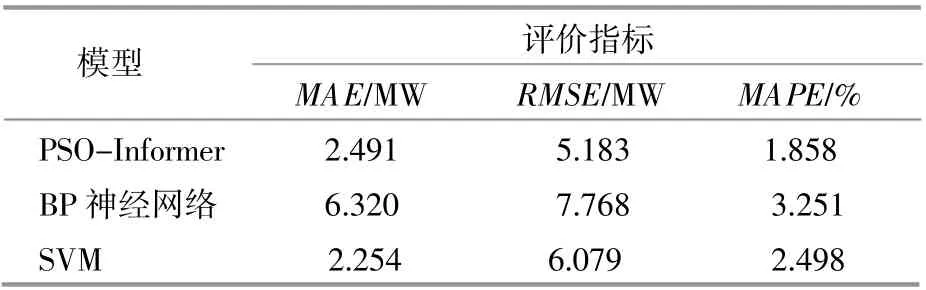
表4 3种模型在测试集上的表现Table 4 Performance of the three models on the test set

4 结论

为了提高地区中长期电量趋势预测精度，本文提出了一种采用PSO优化的Informer模型，有效地解决了长时间序列预测问题。首先从定性和定量角度分析大规模新能源电源接入新型电力系统、外部环境以及节假日等因素对地区电量的影响，在此基础上，建立了Informer电量趋势预测模型。通过概率稀疏自注意力机制和蒸馏操作，解决了模型的时间复杂度和内存使用的问题，并以生成式解码方式输出多步预测值。为了提升Informer模型的预测能力，采用PSO算法对Informer模型的超参数进行寻优，获得最优的电量趋势预测模型。

研究结果表明，与BP神经网络模型和SVM模型相比，Informer模型的预测误差更小，泛化性能更强，适应于中长期电量趋势预测。