一种基于反赫布规则的自适应主分量递归学习算法

何红洲

(绵阳师范学院数理学院，四川绵阳 621000)

0 引言

数据压缩和模式分类已经引起了众多领域研究者的广泛兴趣，这些领域包括模式识别、人工智能和信号处理等[1].数据压缩的目的是发现输入数据的更有效表示以节省空间和处理时间，这种表示即以统计方式从原始模式序列中提取的本质信息，提取过程是将高维的(输入)空间映射到低维的(表示)空间[2].在建模多层感知机网络时，隐层神经元是相应于输入模式最有效表示的一层结点，它是数据压缩的结果，其激活模式可被视为表示变换的目标模式，网络的下一层就是依据目标模式的分类[3-4].

1 问题的一般描述

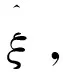
但当矩阵R的阶数、即输入空间的维数较高时，计算其特征值和特征向量是一个高复杂度的问题，因此变换矩阵P很难用纯数学方法得到.近几十年来，变换P自适应计算的新技术不断涌现，这些新技术用迭代的方法计算R的特征向量.Oja提出了一种线性神经网络[7](如图1)，使用一个输出神经元η来计算n个输入随机变量ξ1,ξ2,…,ξn的最大主分量，即η为ξi的带权值qi的线性组合

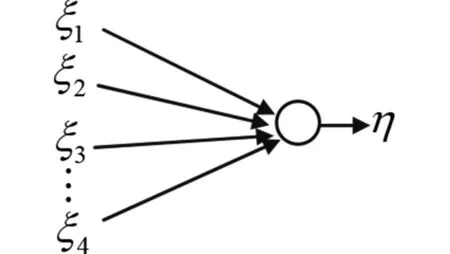
图1 只有一个输出神经元的线性神经网络Fig.1 Linear neural network with an output neuron

或写成更紧凑的形式η=qξ，这里q=(q1,q2,…,qn)和ξ=(ξ1,ξ2,…,ξn)T分别表示权值行向量和输入列向量，权值行向量q按下述规则更新(其中β为学习率参数)：

Δq=β(ηξT-η2q)，

Oja证明了该算法收敛且能提取输入序列的第一个主分量，即在平稳状态下，训练出的向量q就是相关矩阵R的相应于最大特征值的规范化特征向量.

为了将Oja的方法扩展到使用多个输出神经元提取多个主分量(以提取m个主成分为例)的情况，Sanger提出了基于下列更新规则的改进方法[8]：

ΔQ=β[ηξT-LT(ηηT)Q]

(1)

其中η=Qξ，Q为m行n列的权值矩阵，其第i行为各输入结点对第i个输出神经元的权值，LT(-)表示矩阵-的下三角(包括对角)部分.一般而言，输出列向量η的维数不超过输入列向量ξ的维数(即m≤n).同样地，Sanger说明了上述算法收敛到最优线性PCA变换，即在平稳状态下，训练出的Q的前m行为R的相应于前m个最大特征值的规范化特征向量.但Sanger方法的缺陷是在训练每个神经元时使用了非局部的信息，从而存在大量的冗余计算(计算量的比较将第4节给出).为了避免冗余计算，Foldiak提出了结合竞争学习机制的赫布型学习方法[9]，使得不同神经元能更有效地提取不同的特征向量，但Foldiak方法也有缺陷：(1)提取的主分量数必须事先设定，当提取的主成分数动态增加时，整个权值集必须重新训练；(2)该方法不能产生精确的特征向量，而是一个能和主特征向量张成相同向量空间的向量集.

2 模型构建

为了能利用前m-1个主分量有效递归计算出第m个主分量，本研究的目标是需要的主分量个数不是预先知道的情况下能提取随机向量序列的主分量，这种方法能够适应R随着时间慢速变化的情况，这时新的主分量可作为这种变化的补偿而不影响以前已经计算的主分量(这种思想类似于信号处理中的格型滤波：每新增一阶滤波，只需增加一新的格点滤波区，而原来的滤波区不发生任何改变).基于这种思想，本文提出了一种新型的称作APRL的递归神经网络，称为自适应主分量递归学习网络.

图2给出了APRL神经元模型：n个输入ξ1,ξ2,…,ξn通过权值{pij}连接到m个输出η1,η2,…,ηm(pij为第j个输入连接第i个输出的权值)，一个前m-1个输出神经元对第m个输出神经元的m-1个反赫布权值构成的行权值向量ω=(ω1,ω2,…,ωm-1).假设输入是一个平稳随机过程，其相关矩阵有n个互不相同的正特征值λ1>λ2>…>λn，同时也假设前m-1个输出神经元输出前m-1个输出序列的规范化主分量，APRL的最重要特点是：第m个输出神经元能提取与前m-1主分量正交的最大主成量，这就是所谓的正交学习规则[10]，于是有

η=Pξ

(2)

ηm=pξ+ωη

(3)

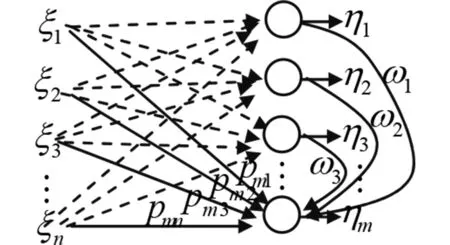
图2 线性多输出网络模型.实线表示在第m个阶段训练出的权值pmj和ωjFig.2 Linear multi-output model. The solid lines denote the weights pmj and ωj which are trained at the m-th stage(注意随着网络收敛，各ωj渐近地逼近于零)(Note that ωj asymptotically approach zero as the network converges.)

这里ξ=(ξ1,ξ2,…,ξn)T,η=(η1,η2,…,ηm-1)T,m-1行n列矩阵P表示输入对前m-1个输出神经元的权值pij构成的矩阵，行向量p表示输入对第m个输出神经元的权值行向量，即p=(pm1,pm2,…,pmn)，即公式(2)和公式(3)展开形式分别为

公式(2)和公式(3)说明：输出的各主分量为输入的线性函数，且第m个主分量不仅与输入对第m个输出神经元的权值有关，还与已产生的前m-1个神经元的输出有关(即多了一项ωη项，这是因为要求第m个主分量与前m-1个主分量正交).

算法的训练针对权值进行，对第m个输出神经元，有

(4)

(5)

其中β和γ是两个正的(可以相等也可以不等)的学习率参数.同样地，公式(4)和公式(5)也可分别展开成

注意公式(4)与Oja的自适应规则一样，这是APRL算法的赫布部分；公式(5)称之为正交学习规则，它是一个反Oja规则，它的形式与Oja规则相似，除了在这一项前面带有负号之外.权值向量ω起到了不断消除前m-1个输出神经元对第m个输出神经元的影响的作用，因此第m个输出神经元最终与以前的主分量正交(而非相关)，这将在下一节给出数学证明并在第4节给出仿真说明.APRL利用Oja规则和正交学习规则的组合产生出第m个主分量.

3 算法的数学分析

假设神经元1到神经元m-1已收敛到前m-1个主分量，即P=(e1,e2,…,em-1)T，这里e1,e2,…,em-1是机关矩阵R的前m-1个规范化的特征向量(列向量)，以e1,e2,…,em-1为基底，令

即向量p(t)在基底e1,e2,…,em-1下的坐标分量为δ1(t),δ2(t),…,δm-1(t)，这里t指扫描的轮数(一轮扫描即包括所有给出的样本输入模式的一轮训练过程).令M为输入模式的总数.

我们将对输出结点的分析分为两段，前m-1个主结点和剩余的新结点(如第m个，…，第n个等).

对于前m-1个主结点，由公式(4)，求第t轮扫描的均值，并假设在t轮扫描期间，p(t)值和ω(t)几乎不变，即E(p(t))=p(t),E(p(t+1))=p(t+1),E(ω(t))=ω(t)，则可得

p(t+1)=p(t)+β′[(p(t)+ω(t)P)R-σ(t)p(t)]

(6)

(7)

之所以有公式(6)，是因为Δp=p(t+1)-p(t),ηm=p(t)ξ+ω(t)η,η=Pξ，由均值的性质知

若对上述公式移项并合并同类项有

p(t+1)=p(t)+β′[(p(t)+ω(t)P)R-σ(t)p(t)]

=[1+β′p(t)(R-σ(t)I)]+β′ω(t)PR，

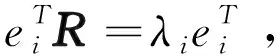
PR=(e1,e2,…,em-1)TR=(R(e1,e2,…,em-1))T=(λ1e1,λ2e2,…,λm-1em-1)T,

故上式展开后，有

由此得

(8)

对公式(5)，令γ′=Mγ，同理可得

(9)

我们用矩阵形式重写公式(8)和公式(9)，有

(10)

当β=γ(β′=γ′)时，上式右端的矩阵有一个二重特征值

ρ(t)=1-β′σ(t)

(11)

如果β′是一个很小的正数，则该特征值小于1，因此所有的δi和ωi都以同样的速度渐近趋于0.

公式(11)说明，若β=γ，选择适当的学习率参数β可以保证收敛速率非常快.特别地，取

β=γ=1/(Mσ(t))

(12)

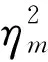
如果β≠γ，则可以非常灵活地选取每个结点i(i=1,2,…,m-1)的衰减速度.进一步，如果针对不同的ωi(即不同的结点)引入不同的参数γi，则对速度的控制就变得更强，因此可有选择地调整参数能使某些结点比其它结点衰减得更快(或更慢).

对于第m个及以后的输出结点i，使用与前m-1个结点处理同样的步骤，但含有ωi的项要从公式(8)中移除，这是因为ω=(ω1,ω2,…,ωm-1)对这些结点没有影响.因此对每个结点i≥m，有

δi(t+1)=[1+β′(λi-σ(t)]δi(t)

(13)

根据前面的结论，对每个i=1,2,..,m-1，δi和ωi将最终收敛到0，因此有

(14)

公式(13)是健壮的，因为即使δi的初值很大使得σ(t)>λi，也有1+β′(λi-σ(t))<1，因此在后续的迭代中，δi也将将大大减小.假设δm(0)以1的概率不为0，定义

则根据公式(13)，有

因为特征值彼此相异，且λ1>λ2>…>λn，所以

且

(15)

(16)

因此

(17)

因此，第m个规范化的组件将被提取出来，Kung给出了以上推导的更多细节[10].结合公式(15)和公式(17)，有

(18)

4 计算效率与仿真结果

基于上述理论分析，APRL算法描述如下：

对每个输出神经元m=1toN(N≤n)

(1)用某些小的随机数作分量将行向量p和ω初始化；

(2)选择公式(4)和公式(5)中的参数β,γ(参见4.1(3)的说明)；

(3)按公式(4)和公式(5)更新p和ω直到Δp和Δω不超过某一阀值.

4.1 计算效率比较

可以验证，APRL算法与已有的算法比较，总计节省了几个数量级的计算量：

(1)递归计算新的主分量的效率

递归计算新的主分量时，APRL每轮迭代算法需要O(n)阶的乘法量；与此对照，Foldiak方法需要O(mn)阶的乘法量，这是由于后者需要计算所有的主分量(包括重新计算已计算过的高阶分量).

(2)使用局部(即侧向结点)算法的效率

APRL算法比Sanger的方法低一阶计算量.更准确地说，在递归计算每一个新分量时，对第m个输出神经元，Sanger方法(参看公式(1))每轮迭代需要(m+1)n次乘法，而APRL算法只需要2(m+n-1)次乘法，这种节省源于APRL只使用了本地的(即侧向的)η结点，这些结点综合了正交训练的有用信息，因此当使用非本地的结点(即ξ结点)时避免了突触权值的重复乘法计算，而在Sanger方法中，这种重复计算是不可避免的.

(3)采用最优学习率β减少了迭代的步数

象公式(12)给出的一样，APRL算法提供了最优估计β,γ的计算公式，但作为另一种更好的选择，替代公式(12)，令

4.2 仿真结果分析

表1 各神经元输出ηi的平方与特征值λi的绝对误差(i=1,2,3,4,5)Tab.1 Absolute error between square of neuron output ηi and eigenvalues λi(i=1,2,3,4,5)

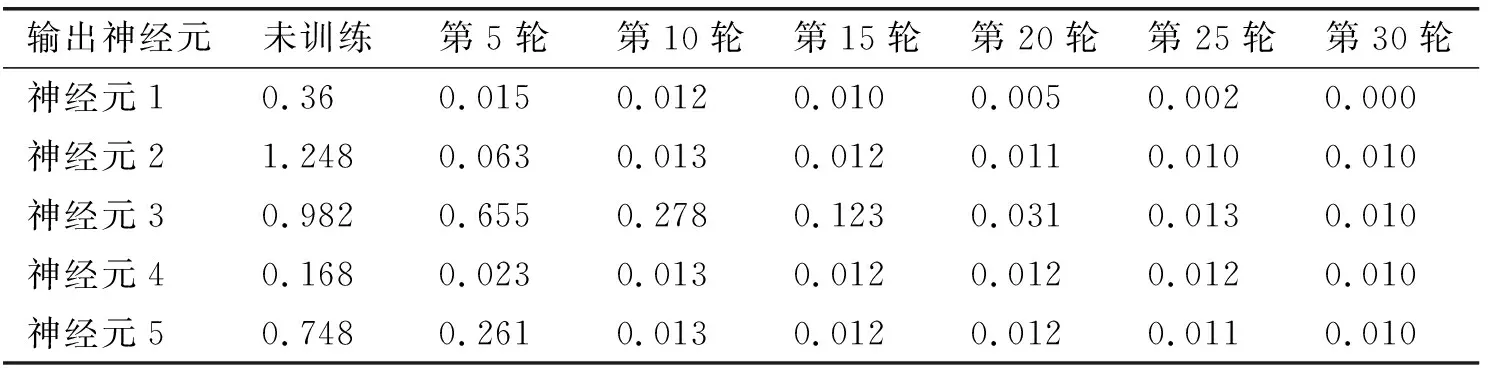
表2 各神经元训练的权值向量p与相应特征向量e的平方距离Tab.2 Square distance between trained weight vector p and eigenvectors e

使用上述的β和γ的取值，算法以相对大的误差收敛，表3第一行给出了收敛速度和最后的计算主分量组件和实际主件的平方距离的关系.为了解决这个问题，需要在微调阶段(即主分量已达到某个近邻值时)使用更保守的学习率参数值，表3总结了使用公式β=γ=1/(Mλm-1f)而f取1,5,10的结果，当f变大时收敛变慢了但同时得到的解也更准确了.

从表3可以看出，使用下面的折中方案，可取得收敛速度和准确度之间的平衡：(a)在初始化阶段，算法取f=1以达到快速收敛(但很粗糙，即误差较大)；(b)在微调阶段，增加f的取值将获得更高的精确度直至到达准确的阀值为止.

5 结语

本文提出了一种新的神经网络学习算法，通过调整学率参数，该算法不仅可以较快速地收敛而且还能达到较高的精度，由于迭代过程中仅使用本地节点的反馈信息及新的主分量的计算可以递归的使用较高阶主分量的计算结果，算法还节约了大量的计算量.论文只针对两种学习率参数相同的条件进行了仿真分析，进一步针对两种学习率参数不同的个性化分析较为复杂，将留待后续的研究.