基于外部认知负荷理论下数学符号逻辑认知顺序探究

张学林，任全红

(绵阳师范学院数理学院，四川绵阳 621000)

0 引言

认知负荷指学习者为了完成所给认知任务，在工作记忆上进行的心智活动所需的全部心智能量.这个理论是由澳大利亚教育心理学家John Sweller等人在上世纪80年代提出的，他们将认知负荷分为三种类型：外在认知负荷、内在认知负荷和相关认知负荷.内部认知负荷是元素间交互形成的负荷，它取决于所需学习的材料的本质与学习者的学科知识之间的交互，教学设计是否得当能不能对它产生直接的影响.而外部认知负荷是超越内部认知负荷的额外负荷，它主要是由教师教学设计不当引起的.“由教学设计引起的工作记忆称为外在认知负荷，外在负荷是可以改变材料呈现方式来改变的”[1].因此学生在初学数学符号、数学公式时教师教学一定要呈现数学符号书写逻辑顺序，有利于学生的主动建构.为此，本文仅从数学符号简述、数学符号不规范和规范的书写顺序的教学、建立和培养学生数学符号意识的教学策略建议等三个方面进行论述,提高数学教学效果.

1 数学符号简述

(1)“数学符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律；知道使用符号可以进行运算和推理，得到的结论具有一般性.”[2]

(2)“符号是文化与传播数学思想的媒体，世界各国都有各自的语言，如汉语、英语、德语、法语……，但数学符号可以世界通用，全世界的人只要受过初等教育都认识下列符号语言，不需翻译如：2+3=5；(a+b)2=a2+2ab+b2;ΔABC∽ΔDEF……”.[3]

(3)“数学符号是数学文献中用以表示数学概念，数学关系等的记号.”数学符号包括几何符号、代数符号、运算符号、集合符号、特殊符号、推理符号、数量符号、关系符号、结合符号、性质符号、省略符号、排列组合符号、离散数学符号等符号，各有各的表示.

为了让学生更容易理解数学符号，笔者认为数学符号是用来表示数学概念、定义、定理、公式、数量(式)间的关系及其运算与推理，从而更方便解决实际问题所用到的符号.“建立符号意识，有助于学生理解符号的意义并进行数学思考.在解决问题中，使学生经历符号化的过程.”[4]

2 培养数学符号的意义

“符号意识作为数学重要的学习内容之一，建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式.”[2]培养和提高学生的数学符号意义获得能力是解决“数学难学”“数学枯燥”“听而不懂”“懂而不会”“会而不对”等教学难题的一种有效的、可行的、具有操作性的途径和方法.对学生提升数学运算素养、提高逻辑推理能力、提升代数思维、培养学生建模能力等方面具有重要的意义，因此，初次教学数学符号时一定要让学生认知数学符号的意义、出现的逻辑顺序以及理解利用数学符号解决数学问题的作用，培养学生的符号意识.

3 初次教学数学符号时出现不规范的书写顺序及矫正

“在教学过程中应尽可能减少外部认知负荷，注意学习材料的呈现方式和教学设计水平有关，呈现形式越合理，越符合学习者的认知水平，学习者的信息加工的干扰因素越少，外在负荷就越低，有利于学习.”[5]学生在没有主动建构数学符号的意义情况下初学数学符号时，要特别注意书写数学符号顺序，体现数学的逻辑性，否则会增加学生的外在认知负荷，教师在教学时对数学符号的书写顺序，如采用汉字从左自右的顺序，易造成学生对数学符号、知识理解困难，缺乏逻辑.因此学生初学时数学教师一定要按照数学逻辑结构书写数学符号，引导学生主动建构，初步形成数感，感受数学符号的作用，初步养成乐于思考、勇于质疑、实事求是等良好品质，不能采取汉字从左自右的书写顺序，避免学生对数学符号不理解，先后的逻辑混乱，造成学生对数学符号产生厌倦，增加学生对数学符号的认知负荷.

(1)学生在学习加法时，教学生运用加法符号“+”时，比如“3与2的和”列数学算式时：不应该从左自右的顺序：书写3+2；应该先写3与2，再写中间的“+”.同理其它几种运算符号也应该这样列式书写，培养学生数学的逻辑思维.一般的老师教学时是按照从左自右的顺序书写算式或解析式.

(2)在学习分数时，应该先写分子、分母，最后写分数线，一般的老师教学时是按照分数线、分母、分子的顺序书写，缺乏逻辑性.

(3)在学习百分数时，让学生真正弄懂百分数的同时，明确百分数的书写顺序，比如82%.按照逻辑顺序应该是先写%，再写82，不应该是先写82，再写%.

(5)在学习绝对值符号时，应该先写数或表示数的字母(或代数式)，再写绝对值符号，比如求-5的绝对值的书写顺序，应该是先写-5，再写绝对值符号，即：-5→||.不应该按照||→-5的顺序.

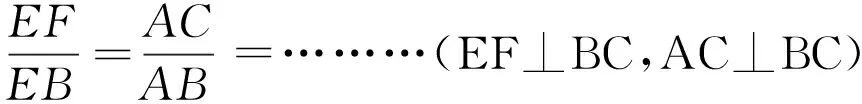
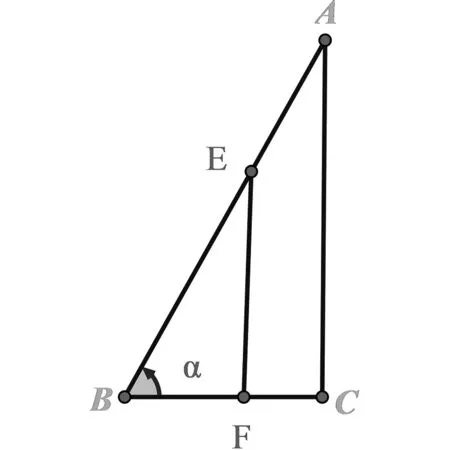
图1 示意图Fig.1 Schematic

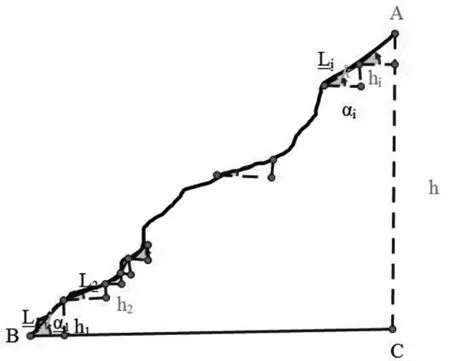
图2 示意图Fig.2 Schematic

(8)在初学某些乘法公式时，也要注意书写顺序，如在学习和的完全平方公式时，其书写顺序为：(a+b)2=a2+2ab+b2，右边的书写顺序为：a2、b2、+、2ab，这与语言文字“两数和的完全平方等于两书的平方和再加上两数积的两倍”相一致.

(9)注意极限符号的引入，比如在计算山高AC的长度时，运用“化整为零、积零成整”的数学思想，首先将曲线山坡化为首尾相接线段L1、L2、……、Ln，AC=h1+h2+......+hn=L1Sinα1+L2Sinα2+……+

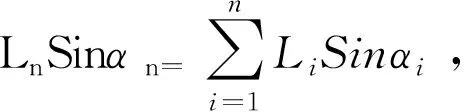
其认知顺序应该是：

的逻辑认知顺序或书写顺序如图2.

4 培养学生主动建构数学符号逻辑认知意识教学策略

“突出知识的形成过程.课程内容的组织要重视过程，处理好过程与结果的关系；课程内容的呈现应注意层次性和多样性.符号意识是将实际问题转化为数学模型问题的基础.”[2]培养学生符号书写逻辑顺序是突出知识的形成过程的一种表象.

4.1 让学生进一步明确数学符号的真正含义

对中小学生来说运用符号不是一件很容易的事，这是因为符号化有一个从具体—表象—抽象—符号化的过程.为此，必须加强数学符号的教学，逐步培养中小学生数学符号逻辑思维能力.

4.2 在教学中注重材料的呈现及数学符号学习的探究过程

教学中特别要注重有关数学符号材料的呈现方式及探究过程，“工作记忆负荷不仅受学生活动的影响，还受材料的内在本质材料呈现形式的影响.”[6]比如在呈现“一只青蛙四条腿，二只青蛙八条腿，三只青蛙十二条腿，问十只青蛙几条腿？”时，应该以诗词的方式呈现学生容易理解：

(利用表格形式进行探究降低学生外在认知负荷)

一只青蛙四条腿，

二只青蛙八条腿，

三只青蛙十二条腿，

……

问十只青蛙几条腿？

同时特别注重数学符号的探究过程，英国著名教育家豪森(A.G.Howson)所指出：“没有必要引入任何符号或缩写，除非学生自己已经深深感受到这样做的必要性，以致于他们自己提出这个方面的建议，或至少当老师提供给他们时他们能够充分体会到它的优越性”.[7]因此在教学中要引导学生探究数学符号的形成过程，让学生真正能感受到引入数学符号的必要.比如学生在学习用字母表示数时，从特殊到一般进行探究，在上述例子中引导学生进一步探究：n只青蛙几条腿？一条直线有一个点有两条射线，两个点有几条射线？n点有几条射线？如果改为线段呢？应该列出表格，引导学生探究.在学习am·an=am+n时要让学生明确乘方的意义，将乘方改为乘法，由不完全归纳法猜出同底幂的乘法公式后，再由am=a×a×a×……×a(m个a相乘)乘法和乘方互相转化进行严密的逻辑证明.

4.3 鼓励学生利用模型思想中的数学符号解决生活中的实际问题

要鼓励学生习惯使用数学符号解决生活实际问题，提高效率，特别是数学建模的有关问题，使用数学符号尤为重要.“数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模过程主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型、计算求解，检验结果、改进模型，最终解决实际问题.”[8]

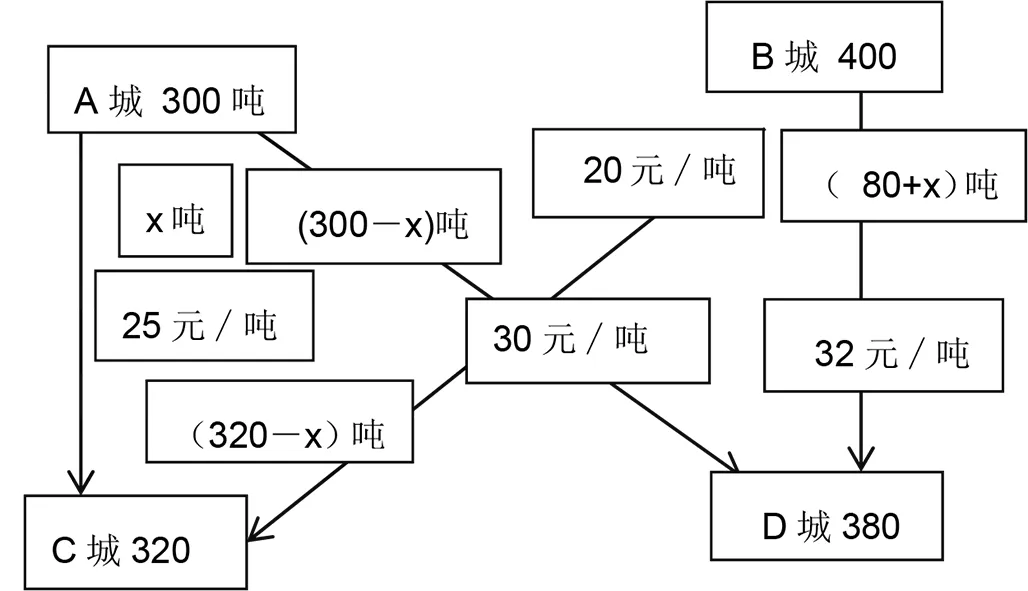
图3 数学计算模型Fig.3 Mathematical calculation model

例 A地有蔬菜300吨，B地有蔬菜400吨，现要把蔬菜运往C、D两市；如果从A城运往C、D两市运费分别为每吨25元和30元，从B地运往C、D两市运费分别为每吨20元和32元；现已知C地需要320吨，D地需要380吨.如果某个体户承包了这项运输任务，怎样的运输方案花钱最少？

分析：引导学生利用字母、箭头、方框图等数学符号表示的数学模型将生活中的实际问题转化为数学问题，再利用数学符号列出解析式，建立数学模型，从而求解.

y=25x+30(300-x)+20(320-x)+32(80+x),即y=7x+17 960.

由题意得，x≥0,(300-x)≥0,(320-x)≥0,(80+x)≥0;解得0≤x≤300,当x=0时，ymin=17 960.

教师这样进行教学设计就大大地降低了学生外在认知负荷.

4.4 通过练习加以强化数学符号的使用，进一步强化数学符号的意义

4.5 遵循学生的认知能力，逐步培养学生数学符号意识

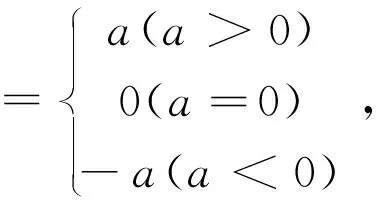
5 结语

总之，教师在面对学生学习新知识，初次教学数学符号时一定要仔细进行教学设计，注重数学知识的逻辑结构，根据逻辑结构确定数学符号的书写顺序，让学生进一步建构认知顺写，减少学生外在认知负荷，激发学生学习数学的兴趣，提高数学教育教学效果.