高中数学直观想象能力的培养
——以“三棱锥切接球问题”为例
江苏省常熟市中学 钱梦迪
1 问题的提出
几何与代数本是数学中最古老的内容,高中数学新课程标准中除原有的双基要求外,思维能力的培养细分到了空间想象、直觉猜想、归纳抽象、符号表示、运算求解、演绎证明、体系构建等[1].其中以直观想象替代原有的空间想象,涉及范围更加广泛,需要对图形进行描述、分析、理解,从而解决数学问题.立体几何中棱锥的切接球(如果一个棱锥的所有顶点都在同一个球面上,那么这个球叫做棱锥的外接球,球体与棱锥的每个面都相切的球是棱锥的内切球)问题,能够发展学生的直观想象能力,但是在学习中,因知识点比较抽象,学生把握不住问题的本质,难以解决.因此在教学中要给学生介绍一些基础的模型知识,培养学生类比思想和空间图形平面化的能力来突破立体几何中的这个难点.
2 正三棱锥的内切球与外接球半径
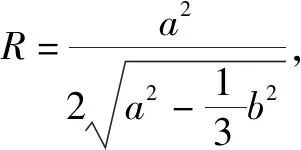
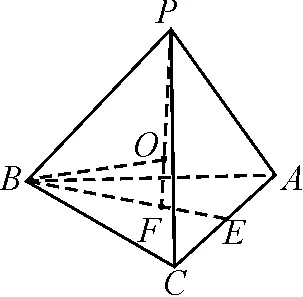
图1
(1)求正三棱锥的外接球半径
已知正三棱锥P-ABC,底面三角形ABC的边长为b,侧棱长为a,PF⊥面ABC,F为垂足,求其外接球半径R.
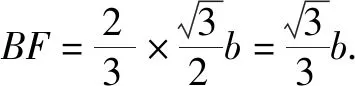

(2)求正三棱锥的内切球半径

图2
已知三棱锥P-ABC为正三棱锥,底面三角形ABC的边长为b,侧棱长为a,求其内切球半径r.
第一步:如图2,取AB中点D,连接PD,CD.设点E,H分别为球与平面APD和平面ACD的切点,圆O为截面圆.
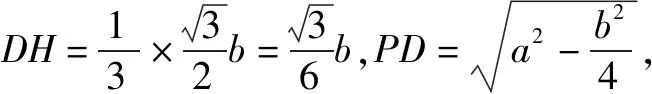
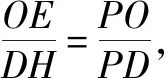
3 培养学生类比的数学思想
在研究正三棱锥内切球的半径时,可类比三角形内切圆半径的求解思路:面积分割,三角形的内切圆圆心到三条边的距离相等,所以三角形的面积等于以三条边长为底,高为内切圆的半径的三个三角形面积之和.因此,三棱锥的内切球半径(内切球的球心到三棱锥四个面的距离都相等)的求解思路:体积分割,三棱锥的体积等于以三棱锥的四个面为底面,内切球的半径为高的四个小三棱锥的体积之和.教学时可利用GeoGebra软件给学生展示(如图3)分割法求内切球半径的动态过程[2].
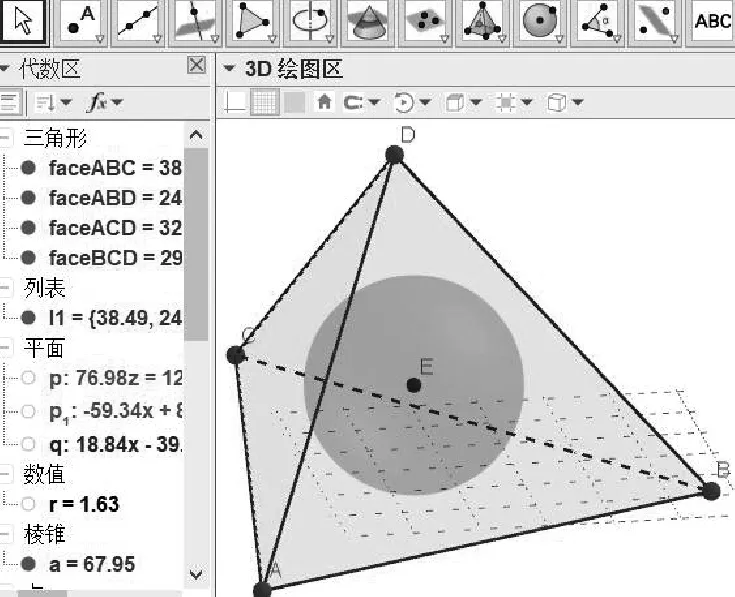
图3
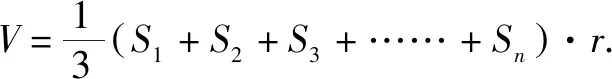
同样地,研究三棱锥外接球半径时,也可以联想三角形外接圆半径的求法.在初中我们先是研究直角三角形外接圆的半径,然后研究钝角三角形、锐角三角形的外接圆半径,都可以通过构造直角三角形来解决.类比这一解题思路,我们研究三棱锥外接球的半径时,也可以通过构造直角三角形来解决[3].
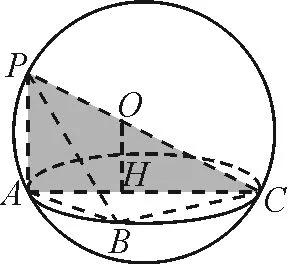
图4
如图4,底面三角形ABC为直角三角形,球心为O,OH⊥平面ABC,H为垂足,设△ABC的外接圆半径为r,则(2R)2=AC2+PA2,或R2=h2+r2,OH=h.
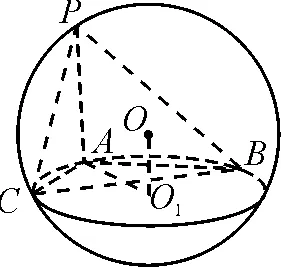
图5
例1已知三棱锥P-ABC的四个顶点都在球O的球面上,若PA=AB=2,AC=1,∠BAC=120°,且PA⊥平面ABC,求球O的表面积.
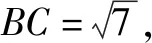
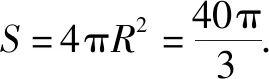
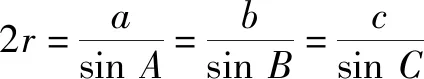
4 用模型解决立体几何问题
利用长方体或者正方体模型来解题,学生的直观感受更加强烈,能够很快分析出球的球心.长方体、正方体模型也是学生学习立体几何的基础.
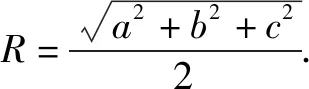
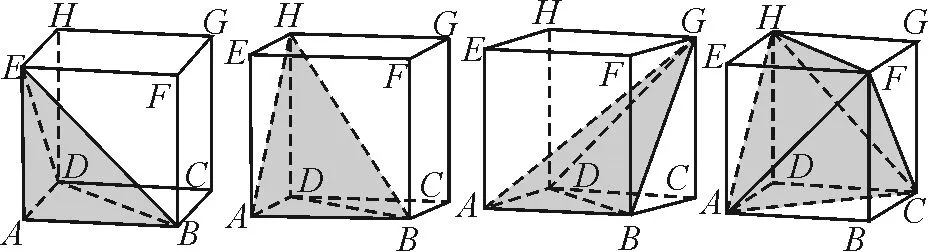
图6-1 图6-2 图6-3 图6-4
例2已知四面体ABCD的三组对棱分别相等,AB=CD=x,AD=BC=y,AC=BD=z,求该四面体的外接球半径R.
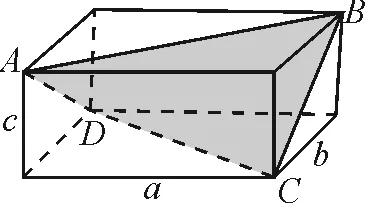
图7
解析:构造长方体,如图7.设长方体的长、宽、高分别是a,b,c,则有
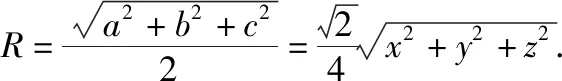
5 结论
总之,立体几何的学习是由浅入深、循序渐进的过程.在这一过程中,要结合概念和定义进行解题训练,体会从感知到操作确认、思辨论证、度量计算的过程,提高学生的直观想象能力.

