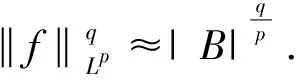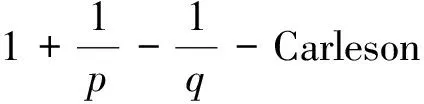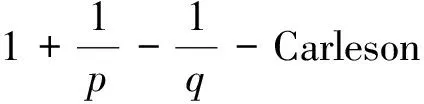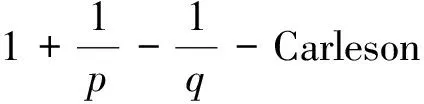Lp()上关于热核的广义面积积分算子研究
李志强,马柏林
(1.浙江师范大学 数学与计算机科学学院,浙江金华 321004;2.嘉兴学院 数据科学学院,浙江嘉兴 314001)
0 引言
其中Da为分数阶导数,f(ζ)为解析函数.一个经典的结果是,对a>0,面积积分算子在Hp()(0 这个算子成为欧氏空间上研究乘子和函数空间的基本工具. 当a=0时,结论不成立.为解决这种问题,文献[3]引入广义面积积分算子 S(I)={z∈:|z|>1-|I|,z/|z|∈I}满足 2008年,文献[5]得出结论: 0 受到上述工作的启发,我们考虑关于热函数的广义面积积分算子 下面,我们研究这个算子的(p,q)型有界性与测度μ的满足条件. 我们引入一些符号.C是正常数,若不特意说明,则取值不一定相同.定义非负函数F,G等价(F≈G):CF≤G≤CF.对于n中的方体Q在中的Carleson型方阵定义为 其中l(Q)为方体Q的边长.n中的球B=B(x0,r)对应中的Carleson型方阵定义为 μ(T(Q))≤C|Q|s. 本文得到的主要结果如下: 主要结论的证明将于后面给出. I(x,t)={y∈n:(x,t)∈Γ(y)}. (1) 为了证明本文的主要结果还需要下面的重要引理. 引理1:当g≥0,g∈Lp(n),1≤p≤∞,有 (2) (3) 则式(2)可替换为 只需要证明 由式(1)可知 证毕. 下面引入关于函数f与热核卷积的非切向极大函数,定义为 证明:对于任意的s>0,令Ω={x∈n:F*(x)>s}. 显然,Ω是一个开集. 记Qk是集合Ω的Whitney分解的小方体,l(Qk)为方体Qk边长,k=1,2,3,….对于每一个x∈Ω,令r(x)=dist(x,Ωc).则对于z∈Qk,有 B(z,r(z))⊆12Bk. 故有 (4) (x,t)∈T(B(x,r(x))). 因此,有 (5) 结合式(4)和式(5),可得 证毕. (6) 证明:我们断言式(6)等价于 (7) 其中G(x,t)=|F(x,t)|q,G*是G(x,t)的非切向极大函数.由式(6),有 显然,式(6)与式(7)等价. 应用Minkowski不等式,得 整理后,式(7)得证. 因为 我们得到N(f)被f的Hardy极大函数控制,结合Hardy极大函数是强(p,p)型,有 C‖M(f)‖Lp≤C‖f‖Lp. f(x)=χ2B(x). 则 对于(x,t)∈T(B),由于 则有 因此,可有 先考虑必要性.设Sμ是强(p,q)型有界的,即 (8) 因此,有 运用Jensen不等式,可得 我们有 由于(x,t)∈T(B),易知I(x,t)⊂2B.通过式(1),有 整理可得 利用对偶性,只需证明对g∈Lq′(),有 (9) 改变积分顺序,有 通过式(1)可知 C‖T*g(y)·N(f)(y)‖Lr. ‖T*g‖Lq′‖N(f)‖Lp 显然,N(f)可以被它的Hardy极大函数所控制,再利用Hardy极大函数的强(p,p)型有界性,得 ‖N(f)‖LP≤C‖M(f)‖LP≤C‖f‖Lp. 再利用引理1 ,有 则 整理得出式(9)成立,于是得到Sμ的强(p,q)型有界性,定理2得证.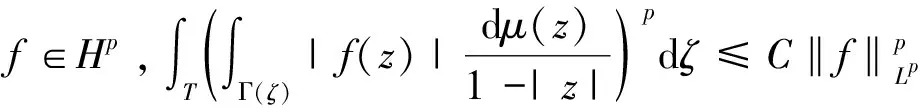
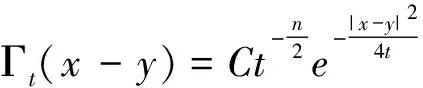
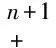
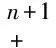

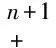
1 预备定理
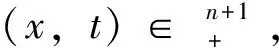
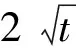
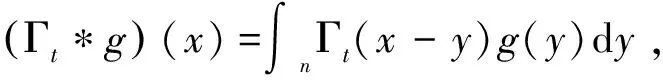
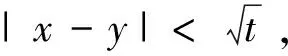
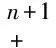
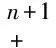
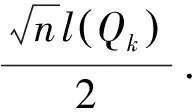
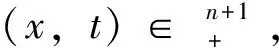
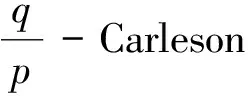
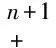

2 主要结果的证明
2.1 定理1的证明
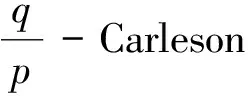
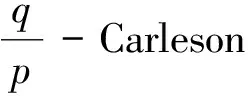
2.2 定理 2的证明