基于频响函数的惯性参数识别改进方法

杜中刚，孙永厚，刘夫云，叶明松，马雪峰，周 星

(1.桂林电子科技大学机电工程学院，广西桂林 541004；2.东风柳州汽车有限公司，广西柳州 544005)

0 引言

惯性参数(质量、质心、转动惯量和惯性积)识别对航空航天、汽车船舰等领域的参数设计及性能控制具有重要意义[1]。基于模态试验的惯性参数识别方法以振动理论和试验模态分析技术为基础，测试的数据不仅包含系统模态质量、模态刚度、固有频率和振型等模态信息，而且可求解系统的惯性参数，它包括模态模型法(modal method，MM)、直接物理参数识别方法(methods of direct physical parameter identification，MDPPI)和质量线法(inertia restraint methods，IRM)[2]。模态模型法利用刚体模态振型关于质量矩阵和刚度矩阵的正交性质[3]，即刚体模态间不发生能量交换，进而求解系统的惯性参数，因此若振型耦合，则识别精度会极大降低，张勇等[4]针对模态模型法中振型识别精度不高问题，提出利用振型之间约束和耦合关系进行修正的方法，但测量复杂构件时，识别精度仍不理想[5]。直接惯性参数识别法利用频域下的动力学方程可一次性识别10个惯性参数，但其对噪声敏感[6]，且采用最小二乘法时会放大误差[7]。质量线法需已知质量，忽略系统刚度和阻尼，分步识别质心、转动惯量和惯性参数，精度更高，更稳定，该方法发展较成熟且已商用化[8]。

质量线法识别惯性参数时，待测构件的质量通常由称重传感器获得[9]，但对大型复杂构件测量难度过大且效率低。何宇翔等[10]通过直接物理参数识别法识别质量，再将质量代入质量线法中识别其余9个惯性参数，但该方法受直接物理参数识别法的精度限制；通过扭振、离心力原理、动量守恒方法也可测得质量，但该类方法受装置条件限制，测取物理量的精度必须足够高，且成本较高[11]。

为解决上述问题，提出基于频响函数的惯性参数识别改进方法。根据振动微分方程和刚体加速度转换关系推导系统各测点的频响函数与刚体质量的关系，考虑待测对象的多样性，对简单、均质的规则构件利用对称性和模态试验获取的频响函数以识别质量；对大型非均质复杂构件利用悬挂法和动力学原理，确定激振位置识别质量，将该方法结合质量线法识别剩余惯性参数。通过对驾驶室和发动机总成的仿真试验，验证本文方法的精度，分析质量误差对质量线法识别剩余惯性参数的影响。通过简单规则构件和某型号卡车驾驶室总成的模态试验对本文方法进行工程验证，结果表明该方法的识别精度完全满足工程要求。

1 惯性参数识别的理论分析

1.1 质量识别的推导

系统的加速度频响函数(frequence response function，FRF)H(ω)由振动微分方程的频域变化得：

(1)

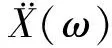
当ω>>ωn时，FRF趋于系统质量相关的定值，如图1所示。对于非纯刚体存在弹性模态且刚体模态趋于0，将在刚体模态和第1阶弹性模态之间相对平滑的频段，称为质量线，通过计算该段内的实数值即可得到系统的质量[12]。

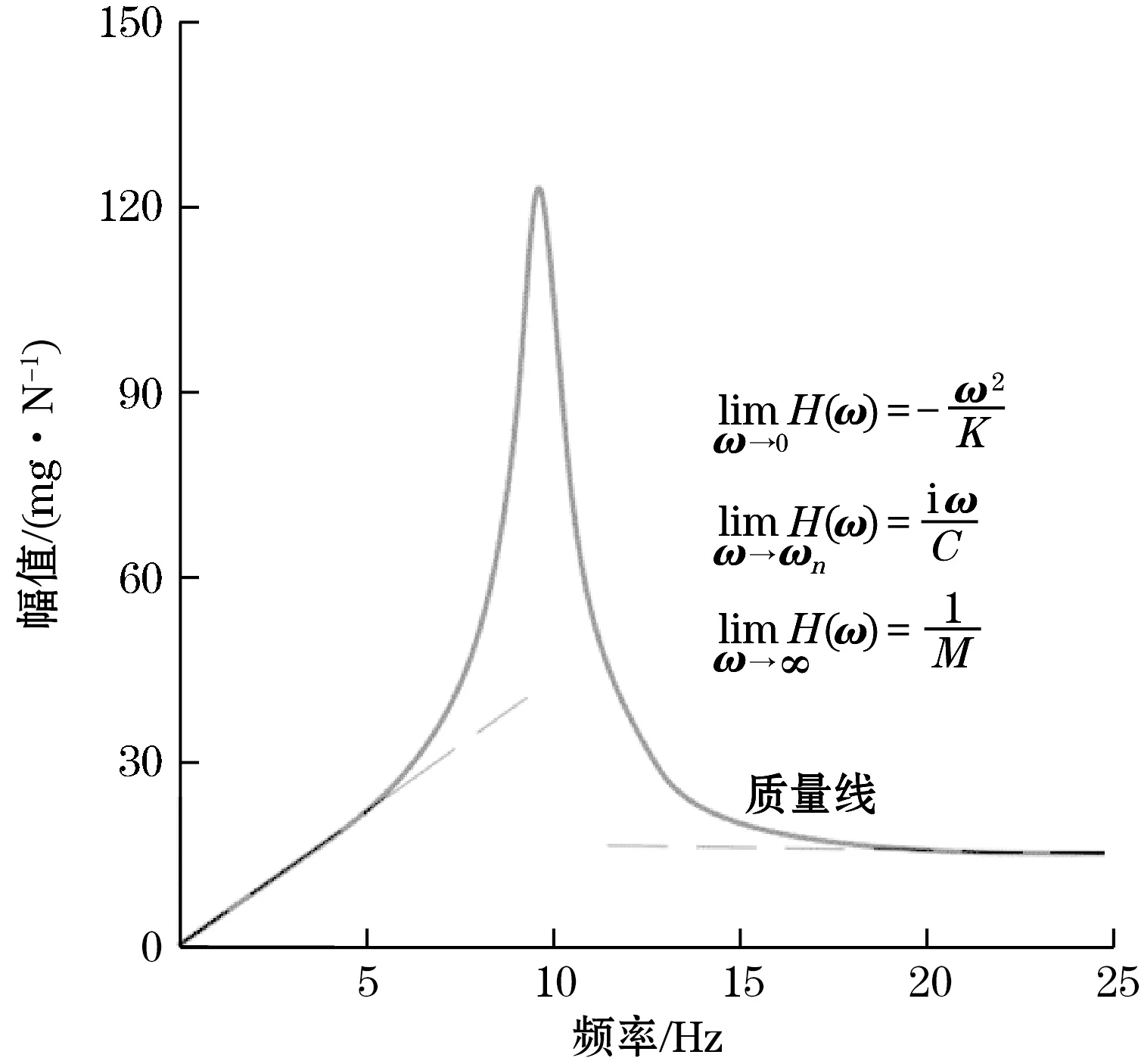
图1 单自由度和多自由度的FRF曲线

根据刚体运动中加速度之间的转换关系可得：

(2)

由式(2)可得，质心处加速度和测点加速度关系为

(3)

可知激振确定时，响应点在激振方向上的加速度由非激振方向的坐标值决定，对式(3)左右两边同乘以1/Fj，得：

(4)

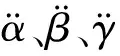
1.1.1 密度均匀的大型对称构件

当被测对象为密度均匀的大型对称构件时，在构件边角位置布置加速度传感器，根据式(2)、式(4)可知加速度频响函数、坐标、质量之间可互相转换，因此在任意边角点按参考轴方向激振，以任意边角的加速度为参考值，根据平面图形的形心坐标与边角坐标关系，便可确定待测对象的质量。以对称刚体为例，在响应点4进行y方向激振，如图2所示。

图2 对称构件算例

通过4个顶角的频响函数求解立方体质量：

式中：H1、H2、H3、H4、Hc分别为响应点1、2、3、4及质心处的频响函数。

为提高识别精度，可布置多个响应点(仅激振方向坐标值不同)，通过均值计算提高识别精度。

1.1.2 非规则的大型复杂构件

当被测对象为非规则的大型复杂构件时，利用自由模态试验可知，其自由边界通过弹性悬挂或支撑达到近似自由条件，因此根据力矩平衡方程[13]，利用悬挂点或支撑点与系统质心的关系，可得：

(5)

式中：p为悬挂或支撑数量；Fp为拉力或支撑力；lpc为Fp到质心的距离。

由式(5)可知，在各点拉力或支撑力相等，且待测系统平衡静止情况下：当p=1时，系统为保持平衡，质心与重心重合，且必在悬挂或支撑点所在的重力方向的垂线上[14]；当p=2时，质心在悬挂或支撑点连线中某点在重力方向的垂线上；当p≥3时，质心在悬挂或支撑点连接平面图形形心在重力方向所在的垂线上。如图3所示，一般p∈[1,4],因此待测系统的质心系轴线与待测系统表面交点的位置可通过悬挂或支撑的布局确定。

图3 悬挂方式与质心关系

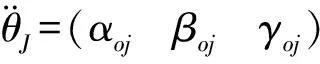
(6)

式中：Jc为待测刚体相对质心的转动惯量；ρjc为质心到激振力作用线的距离。

当ρjc=0时，相对质心系的角加速度为0，且对各测点在激振方向的频响函数值作最小二乘法求解，即可识别系统的质量。

1.2 质量线法

建立质心坐标系C-XYZ和原点参考坐标系O-XYZ，当式(1)中M为广义质量时，得质心处为Mc：

(7)

式中：(JxxJyyJzz)为绕质心坐标系X/Y/Z轴的转动惯量；(JxyJyzJzz)为相应坐标平面的惯性积。

(8)

结合式(8)质心处的激振力、质心加速度及识别的质量，即可确定质心坐标为

(9)

式(9)有3个未知数，通过1次激振可粗略计算质心坐标，根据刚体动量矩定理得包含转动惯量和惯性积的矩阵Jcc为：

(10)

Jcc中有6个未知数，因此m≥2，n≥3时，用最小二乘法可提升识别剩余惯性参数的精度[15]。

2 惯性参数识别的仿真分析

2.1 密度均匀的大型对称构件

为分析并验证密度均匀大型对称构件质量的识别方法，将近似规则均质的某商用车驾驶室三维模型通过Hypermesh中Opstruct模块网格划分和材料属性设置等前处理操作，导出MNF文件到Adams/View中建立模型，采用4根线性弹簧阻尼器将其悬挂，使其边界近似自由，如图4(a)所示，采用Marker点创建激振点和响应点，其中响应点选择驾驶室中相对规则的地板处进行对称布置，激振点布置在角加速度大的位置，利用Adams/Vibration振动分析模块，分别在激振点和响应点上建立输入和输出通道，通过预试验判断刚体模态频率在2 Hz左右，设置带宽256 Hz，分辨率为0.5，在Adams的后处理模块中，确定各响应点X/Y/Z方向的频响函数，如图4(b)所示，对频响函数60～100 Hz频段的数据，按1.2方式进行质量计算，驾驶室质量识别为307.3 kg，计算值相比参考值降低了0.3 kg，质量识别相对误差为0.1%，因此本文方法在大型对称构件上的仿真精度满足工程要求。

(a)驾驶室模型

2.2 非规则的大型复杂构件

为验证非规则大型复杂构件识别的质量，将某型号发动机总成按驾驶室模型处理方法建立振动试验模型，采用2根线性弹簧阻尼器将其悬挂，考虑质心位置的确定，需对悬挂位置坐标调整，保证每根弹簧受力相同，如图5(a)所示，可知各响应点在激振方向的频响函数基本相同，选择各平滑频段内数据作均值处理，如图5(b)所示，根据1.2方法，确定其质量为188.05 kg，相比参考值增加0.574 kg，相对误差为0.31%，因此该方法适用于非规则大型复杂构件质量的识别。

(a)发动机模型侧视图

为进一步识别剩余惯性参数，首先以发动机总成模型研究质量误差对剩余惯性参数的影响，如图6所示，剩余的9个惯性参数识别误差受质量误差影响，其中转动惯量和惯性积受其影响较大，质心影响较小，当质量误差≤10 kg时，剩余惯性参数绝对误差均不超过0.05，因此，剩余惯性参数识别精度对质量误差不是非常敏感。

图6 质量误差对剩余惯性参数的影响

综上所述，将本文方法识别的质量结合质量线法识别发动机总成的剩余惯性参数并对误差进行对比分析，如表1所示。

由表1可知，发动机识别的Y向质心坐标误差为5.9%，惯性积中Jxy和Jyz相对误差较大，主要原因受Y向悬挂的影响，转动惯量最大相对误差小于0.2%，因此整体惯性参数识别的精度满足工程误差要求。

表1 发动机仿真实验识别的惯性参数

3 实验验证

3.1 密度均匀的对称构件

为验证本文提出的方法，首先对密度均匀的对称构件进行验证，对未知惯性参数的均质规则构件采用LMS设备采集输入输出的数据、型号为PCB 356B18和3263A2的三向振动传感器测取加速度，型号为INV9313且灵敏度为0.21 mV/N的橡胶头力锤进行激振，结合ImpactTesting软件对数据分析筛选，激振和响应坐标通过六自由度的FARO-Arm关节臂和PowerINSPECT软件相互结合测量坐标，其单点精度≤0.025 mm(2σ)，测量范围为2.4 m，可完全测量各坐标值，如图7所示。

图7 简单件模态试验

通过预实验确定刚体模态1 Hz左右，确定采集频率为512 Hz，谱线数为1 024，带宽为256 Hz，按本文方法对其采集数据进行分析，确保试验过程无欠载和过载信号，相干函数幅值≥0.9，输入信号和输出信号的刚体相关系数都在95%以上，平均相关性在99%左右，结合传感器的位置坐标，选择相对平滑的频段识别出质量，并结合质量线法计算剩余惯性参数，如图8所示。

(a)频响函数

已知构件的密度和尺寸，以SolidWorks中建立该模型的惯性参数为参考值，确定参考坐标系，将其与模态试验识别的结果对比分析，由于该构件中心对称，惯性积过于微小不做考虑，如表2所示。

表2 密度均匀对称构件的惯性参数

由表2可知，质量识别相对误差1.88%，转动惯量误差较大，但其整体最大误差不超过4%，质心最大误差不超过2%，识别精度满足工程要求。

3.2 大型复杂构件

对大型复杂构件的验证以某型号驾驶室进行模态试验，考虑其受力状态选用相同型号的弹簧进行悬挂点布置。由于其体大且过重，激振选用灵敏度为0.05 mV/N的IEPE型冲击力棒进行激振，如图9所示，试验参数设置采样率为320 Hz，谱线数为1 024，布置18个三向振动传感器，其余试验设备与简单构建试验的相同，采用单点激振多点响应方式获取数据并对每次激振的数据进行5次平均，根据相干性、输入/输出信号的刚体相关系数筛选频响函数，选取刚体模态和第一阶弹性模态之间较光滑的频段进行均值计算，将识别的质量结合质量线法计算剩余惯性参数。

图9 驾驶室的模态试验

为对驾驶室识别的参数进行比较分析，采用商用化的MPC转动惯量平台对驾驶室进行测量，其测量的质量误差小于1 kg，质心精度小于3 mm，转动惯量小于2%。首先按顺时针选择工作台面上3个基准点，测量其与3个特征点距离，将其作为坐标系变换的参数，再分别测量驾驶室6个姿态在空载和载重时的惯性参数，汇总后计算出质量、质心、转动惯量和惯性积，如图10所示。

图10 MPC转动惯量平台测试驾驶室

将2种方法测试的惯性参数进行对比分析，如表3所示。由表3可知，由于驾驶室总装较大，结构复杂，导致整体识别值有偏小，在质量识别中误差达到4.502%，因为驾驶室尺寸很大，则质心识别相对误差较小，最大不超过2%，转动惯量受质心坐标误差影响，最大相对误差为Jzz的8.81%，惯性积整体最大误差不超过3%，同时受质心误差影响，Jyz误差最大为2.79%，综上所述，该方法识别的惯性误差满足工程要求。

表3 驾驶室的惯性参数

4 结束语

本研究利用刚体振动微分方程和加速度转换的关系，推导频响函数与质量的关系表达式，基于该式细分2种确定系统频响函数与质量等效转换的方法。联合Hypermesh和Adams分别搭建驾驶室和发动机总成的振动仿真模型，并比较本文方法的精度。分别对简单构件和某型号驾驶室进行模态试验，将本文方法结合质量线法识别惯性参数，通过对驾驶室识别结果与MPC转动惯量平台测试结果的对比分析，验证该方法的工程测试精度。研究结果表明：

(1)本文所提出基于频响函数的惯性参数识别改进方法在识别质量时，仿真相对误差最大不超过0.4%，实验测量相对误差最大不超过4.6%；综合该方法结合质量线法识别的惯性参数结果分析可知：质心坐标相对误差≤2%，转动惯量相对误差≤9%，惯性积相对误差≤3%，因此本方法满足工程实际应用需求。

(2)质量线法中剩余惯性参数误差对质量识别误差不十分敏感，但质心坐标对转动惯量和惯性积影响较大，且本文方法对密度均匀且对称构件的质量识别精度更高。