基于改进SPI的多量程MEMS虚拟陀螺研究
张国亮,曾 成,2
(1.河北工业大学电子信息工程学院,天津 300401;2.天津市电子材料与器件重点实验室,天津 300401)
0 引言
由于微机电系统(micro electro mechanical system,MEMS)陀螺仪具有低精度、漂移高的缺点,不能满足高精度的定位需求[1]。2003年,文献[2]提出虚拟陀螺技术,即选用多个成本低、精度一般的陀螺构成阵列,对相同目标进行角速度检测,通过滤波融合方法输出一个估计的高精度角速率值。目前,MEMS虚拟陀螺研究[3-5]大都侧重于利用同一类型、同一量程的MEMS虚拟陀螺数据融合来达到提高角速度测量精度的目的。但是对载体运动动态范围很大的情形,单一量程的陀螺在工作过程中难以兼顾大动态量程和高传感器精度的要求。
为此,本文设计了新型多量程MEMS虚拟陀螺。首先通过改进SPI方式完成传感器阵列数据读取,然后将虚拟陀螺数据进行Allan方差分析和基于一阶AR模型的卡尔曼滤波数据融合,最后对比在静态条件下,相同个数与型号的虚拟陀螺在选择不同量程数据进行融合时的滤波融合效果、1σ标准差以及陀螺仪各项噪声降低效果;在同一次动态实验中,对比多量程虚拟陀螺与单一量程虚拟陀螺通过姿态解算获取的姿态变化轨迹与最终姿态角解算精度。
1 多量程传感器阵列系统搭建
1.1 虚拟陀螺模块
本文采用运动型六轴传感器ICM42605搭建多量程虚拟陀螺,该传感器包括三轴陀螺仪与三轴加速度计,可供选择量程范围广,符合本课题研究,可通过软件选择量程包括±15.625(°)/s,±31.25(°)/s,±62.5(°)/s,±125(°)/s,±250(°)/s,±500(°)/s,±1 000(°)/s,±2 000(°)/s,考虑到成本以及虚拟陀螺随着规模扩大,提升效果逐渐减弱,选择16个同类型传感器搭建阵列,采用量程与个数配比如表1所示。

表1 虚拟陀螺量程个数配比
1.2 改进SPI数据读取方式
ICM42605的SPI通信速率最高可达到24 MHz,STM32F429IGT6通过晶振倍频输出频率可达到180 MHz,SPI的时钟信号线频率可通过波特率发生器进行分频,输出速率最高可达22.5 MHz。当单独读取一个ICM42605数据时,需要读取三轴陀螺仪数据、三轴加速度计数据、温度传感器数据,共7轴数据,每轴输出数据都是16位,单个传感器读取时间为4.98 μs。当用1组SPI与16个普通GPIO作为传感器软件片选读取16个ICM42605数据时,读取时间为79.64 μs。考虑到惯性传感器数据具有同步性,不可延时,尽量缩短一次采集过程所需时间,提出了一种新型数据采集方式。
本系统采用改进SPI方式完成数据读取,如图1所示,使用主控芯片STM32F429IGT6 4组SPI外设SPI2、SPI3、SPI4、SPI5,每组SPI控制4个传感器工作在一种量程,共用该组SPI的SCK、MISO、MOSI。片选选用SPI硬件片选,将硬件片选信号与4组SPI共用的4组GPIO-CS1、CS2、CS3、CS4作为或门芯片SN74LV32ADR输入电平,将或门输出电平作为传感器片选输入信号。例如当CS1输出低电平时,同时使能4组SPI硬件片选,可同时选通CS1控制的4个传感器,实现SPI硬件片选下的一主多从,读取时间可缩短1/4。

图1 阵列数据读取方式
数据读取过程中利用SPI的DMA(direct memory access,直接存储区访问)模式,DMA在不占用CPU时可实现内部存储与各种外设之间高速搬移数据,将4组SPI分别配置为不同DMA数据流,不同SPI可实现数据同时读取,保证数据实时性。初始化各种外设后,进入定时中断,完成传感器数据读取与数据合并,在4组SPI各自DMA中断中取消使能硬件片选,清除中断标志,给予共用GPIO高电平,断开传感器与SPI之间通信,在定时中断外将传感器数据进行整合。
1.3 硬件系统平台
本实验搭建的硬件系统平台,如图2所示。

图2 硬件系统平台
2 多量程虚拟陀螺滤波融合方法
对于内含多种噪声的信号,需要将干扰噪声滤除,卡尔曼滤波因其使用条件低,被广泛应用。在对陀螺仪数据进行滤波前,需要针对陀螺仪随机误差进行分析获取建模因子,本系统采用式(1)一阶AR模型,针对实际角速率状态进行建模[6]:
ωk=-bωk-1+μk
(1)
式中:b为模型参数;μk为零均值白噪声。
卡尔曼滤波的状态方程表示为
XK=AK·XK-1+ζK-1·ψK-1
(2)
式中:ψ为系统噪声,cov[ψn,ψm]=qδnm,E[ψK]=0;XK=ωK;AK=-b;ζK-1=1。
多量程MEMS虚拟陀螺虽然由16个传感器组成,但是每次只选择一种最佳量程,即选择4个传感器数据进行融合,K=1,2,3,4。
观测方程为
Zk=CK·XK+φK
(3)

本系统采用同一型号传感器组成阵列,利用其相关性可进一步优化滤波融合技术,则观测噪声协方差矩阵R为
(4)
式中:ρnm(n,m=1,2,3,4)为传感器相关性系数;σ2为陀螺仪噪声方差,通过Allan方差法[7-8]获得。

预测下一步方程:
(5)
均方误差预测:
PK|K-1=APK-1|K-1AT+ψK
(6)
滤波增益矩阵:
KK=PK|K-1CT|(CPK|K-1CT|+φK)
(7)
状态估计方程:
(8)
均方误差更新:
PK|K=(I-KKC)PK|K-1
(9)
3 姿态信息获取
动态条件下虚拟陀螺的提升效果可通过解算虚拟陀螺的输出姿态轨迹与最终姿态角解算精度得出。常见的姿态角解算算法有欧拉角法、方向余弦法、四元数法等,其中四元数法[9]因其计算量小、精度高,可避免奇异性被广泛使用在姿态解算上。四元数姿态解算变量为
Q(q0,q1,q2,q3)=q0+q1i+q2j+q3k
(10)
式中:q0、q1、q2、q3为实数;i、j、k是相互正交的单位向量。
四元数微分方程为
(11)

(12)
式中:ωx、ωy、ωz分别为陀螺仪在载体坐标系下绕X、Y、Z轴的角速度。
因该阵列计算数据量少,得到陀螺仪的三轴角速度后,根据以下公式更新四元数。
(13)
(14)
(15)
(16)
式中T为采样时间。
由于在计算过程会产生误差,需要对更新的四元数进行归一化处理,处理完毕即可根据以下公式进行姿态角解算:
(17)
Y=-arcsin[2(q1q3-q0q2)]
(18)
(19)
4 实验分析
4.1 静态测试
将多量程虚拟陀螺系统置于静止转台上,初始化虚拟陀螺,静置1 h,等待陀螺仪输出数据稳定后,以200 Hz的采样频率连续采集5 h的数据,取其中3 h数据进行实验分析。
在同一次静态测量中,每种量程陀螺个数都是4,将4种量程离线数据分别完成进行Allan误差分析与滤波融合,以X轴为例,得到如图3~图6所示的结果,从图中可以看出虚拟陀螺经过滤波后输出信号的噪声都有很大程度降低。

图3 ±15.625(°)/s量程虚拟陀螺融合效果

图4 ±62.5(°)/s量程虚拟陀螺融合效果

图5 ±125(°)/s量程虚拟陀螺融合效果

图6 ±2 000(°)/s量程虚拟陀螺融合效果
根据所选量程的不同得到的融合效果也不同,±15.625(°)/s量程虚拟陀螺效果最佳,±62.5(°)/s量程虚拟陀螺,±125(°)/s量程虚拟陀螺,±2 000(°)/s量程虚拟陀螺融合效果依次减弱,且其原始信号噪声逐步增大。
对不同量程下陀螺组合阵列的原始数据与融合数据进行1σ标准差分析,如表2所示。以X轴为例,4种量程组合阵列1σ标准差的均值分别为0.249 5(°)/s,0.321 2(°)/s、0.449 1(°)/s、0.494 0(°)/s,融合后分别为0.057 9(°)/s、0.097 8(°)/s、0.160 1(°)/s、0.183 8(°)/s,分别降低了76.8%、69.5%、64.4%、62.3%。

表2 1σ标准差分析
分别对4种组合量程阵列进行Allan方差数据拟合得到随机噪声数值,表3列举了角度随机游走,零偏不稳定性,量化噪声的原始数据与经过滤波融合后输出数据。
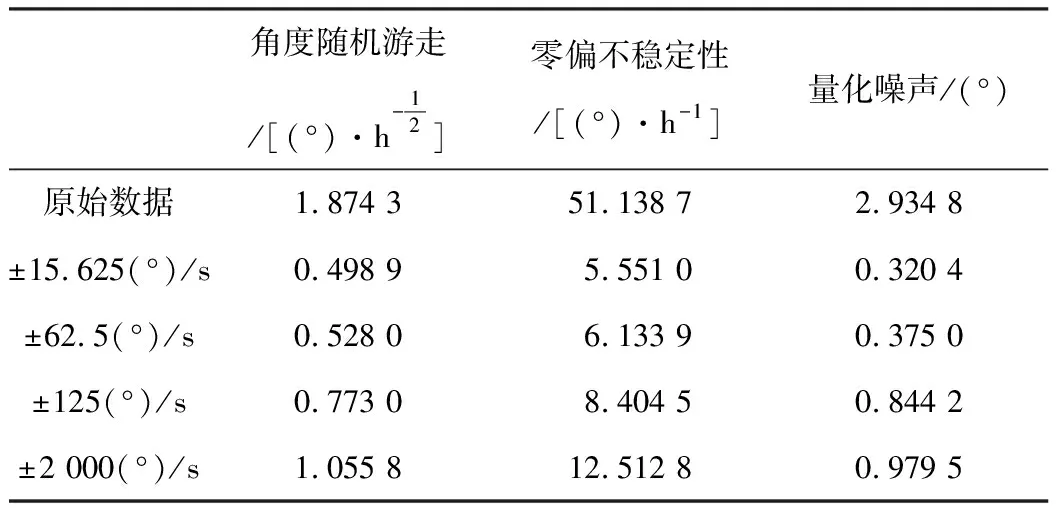
表3 滤波后的误差提升效果
从表3可得,经过滤波后噪声数值都有所降低。零偏不稳定性是衡量虚拟陀螺性能的主要参数。该陀螺仪的原始零偏不稳定性数据为51.1 387(°)/h,经过滤波融合后,4种量程阵列零偏不稳定性数据分别为5.551 0(°)/h、6.133 9(°)/h、8.404 5(°)/h、12.512 8(°)/h,分别降低了89.1%、88%、83.6%、75.5%。
静态实验结果表明,当检测对象处于静态时,多量程MEMS虚拟陀螺可选择最小量程数据进行融合,得到的检测效果要优于大量程阵列。
4.2 动态测试
将多量程MEMS虚拟陀螺置于转台上,静置30 min,等待输出数据稳定后,进行模拟载体大动态实验,控制读取时间相同,在动态行为结束后,将虚拟陀螺置于起始位置,采集15~20 s数据。
在同一次动态实验中,数据采集完成之后,对整个过程离线数据进行预处理,首先对所有传感器陀螺仪数据进行判断,将超出量程的数据用nan代替,将数据进行滤波融合时,输入16个传感器三轴陀螺仪数据,利用Matlab中isnan函数进行判断,将不是nan的数据重新整合到数组中,根据数组长度判断,每次动态选择4个相同量程的数据进行融合,长度与量程关系如表4所示。

表4 数组长度与量程数据选择关系
数据预处理与滤波融合后,对整个过程利用四元数方式进行姿态角解算,通过解算阵列回到起始位置时数据的精度可以衡量整个虚拟陀螺系统在大动态下的性能,以X轴为例,实验结果如图7~图9所示。

图7 多量程虚拟陀螺姿态变化
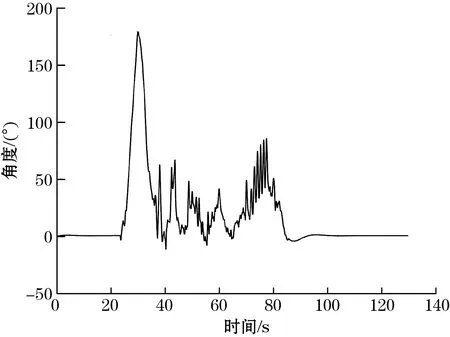
图8 ±2 000(°)/s量程虚拟陀螺姿态变化

图9 ±15.625(°)/s量程虚拟陀螺姿态变化
从图7~9中可以看出,在模拟大动态条件下,多量程虚拟陀螺,±2 000(°)/s量程虚拟陀螺能解算出相似的姿态变化轨迹,最终姿态角偏离程度小;±15.625(°)/s量程虚拟陀螺解算结果与二者不符,且最终姿态角偏离程度大。
分别对3类阵列再次置于起始位置时姿态数据作残差分析,实验结果如表5所示。

表5 最终姿态角残差分析
从表5可以看出,3种量程组合下,虚拟陀螺解算出X轴最终姿态角分别为0.181 9°、0.335 8°、10.040 8°。实验结果表明:多量程MEMS虚拟陀螺最终姿态角解算精度要优于单一量程虚拟陀螺,更接近真实情况。
5 结束语
本文设计了多量程MEMS虚拟陀螺,利用改进SPI数据读取方式,提高了数据读取速率。在静态实验中,分析对比相同数量虚拟陀螺选择不同量程时阵列融合效果、1σ标准差以及降噪能力,由实验数据可知,多量程虚拟陀螺1σ标准差降低了76.8%,零偏不稳定性下降了89.1%;在动态实验中,多量程虚拟陀螺不仅能获取与大量程虚拟陀螺相似的姿态变化轨迹,还能获得优于单一小量程阵列的姿态解算精度。实验结果说明:静态和动态实验下,多量程MEMS虚拟陀螺的姿态监测与降噪能力效果优于单一量程虚拟陀螺。

