基于单门限二元检测的课堂思政教学设计
麦超云 甘俊英 秦传波 曾军英 徐颖


关键词:信号检测与估计;二元检测;教学设计;思政元素
1引言
2017年,教育部印发的《高校思想政治工作质量提升工程实施纲要》将课程育人列为“十大育人”体系之首[1]。课程思政不是特定的一门或一类具体教学科目以及某一教育活动,课程是泛化的概念,即学校育人的所有教学科目和教育活动都渗透和贯穿着思政教育,其特点是课程为载体,思政教育是灵魂,课程的育人功能和价值取向鲜明,而传统的课程边际淡化。课程思政是一种课程观,是将高校思想政治教育融人所有课程教学和改革的各环节、各方面,围绕“知识传授与价值引领相结合”的课程目标,充分发挥包含专业课程在内的其他所有课程的育人价值[2]。
各高校针对课程思政都有自己的思路,总结教学中的实践结果,提出不同观点。本文以“信号检测与估计”课程中的二元检测章节为例,结合时政热点,将思政元素融人课堂教学设计[3]。因为二元假设检测是最基本的检测问题,所以在“信号检测与估计”课程经典检测理论教学中,首先讲述二元假设检测,其中介绍的相关概念和模型在后续的课程内容中都会沿用。事实上,雷达目标检测和二进制数字通信就是典型的二元假设检测问题。
2课堂内容介绍
典型的二元假设信号检测理论模型主要由四部分组成,即信源、概率转移机构、观测空间和判决规则。图1为二元假设信号检测理论模型。
如图1所示,信源产生假设:概率转移机构是在信源输出的其中一个假设为真的情况下,把信号以一定的概率关系映射到观测空间,即按照某种概率规则在观测空间产生一个点:判决规则使观测空间的每一个点对应一个相应的假设,或者说判决规则实际上就是对观测空间的划分规则。
在二元假设检验理论中,信源输出两个假设: Ho和H1。H0称为零假设,日,称为备择假设。比如,在雷达系统中,雷达对特定区域进行观测并判定该区域是否存在目标,通常假设Ho表示目标不存在,假设H1表示目标存在。
3教学设计:问题引入
课堂教学开始时,一般通过例子引入基本概念。举例:将“雷达检测导弹”场景作为例子,并简化大部分设定,以便更好地说明二元检测问题。
设地面基站有雷达装置,用于检测敌方导弹袭击。雷达发射信号幅值为1,传播过程中只会被导弹反射信号:反射和传播过程中信号不衰减:不考虑时延t;敌方发射导弹袭击的概率为1/2。
在这些设定下,如果没有噪声,信源信号将映射到观测空间的某一个确定的点,即可以百分之百概率正确检测到导弹目标。现在,假定有加性噪声干扰,噪声是均值为0、方差为1的高斯噪声n。如此,在两个假设下,观测信号模型为:
根据已知条件,可以写出两种假设下观测信号的概率密度函数,分别为:
信源输出的信号将以一定的概率映射到整个观测空间,而映射到某一点附近的概率取决于概率密度函数p(yIHt)和p(yHo)。
4教学设计:教学互动
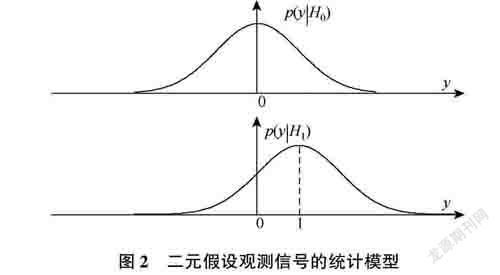
在课堂教学中,将图2中的p(y 1 Hi)和p(y 1Ho)画在同一个坐标中,如图3所示。同时,发起教學互动,提出疑问和讨论,让学生循序渐进地理解二元检测问题的相关概念。
4.1问题一:接收信号的范围
该问题可以由式(2)、式(3)和图3直观得出结论,即接收信号的范围是负无穷到正无穷。
4.2问题二:极端信号的来源
由问题一可知,接收信号的范围是负无穷到正无穷。设接收到一个数值为-100的样本,它的来源有没有可能是H1;另一个数值为200的样本,它的来源有没有可能是Ho?由图3可以看出,以上两个问题的答案都是肯定的。
4.3问题三:判决门限的概念
由问题二可知,任何一个样本都有可能是由假设Ho或者由假设日,产生,因此需要确定一个规则,引入“判决门限”的概念。图3中在横坐标约0.8位置处黑色竖直线表示判决门限。样本值落在判决门限右方的,判决为H1;样本值落在判决门限左方的,判决为H0。
5教学设计:深入探讨
解析四种情况与两类错误。图4中概率密度函数的两条曲线与判决门限的竖直线将图形分割成四个部分,分别对应二元检测的四种情况。
5.1情况一:正确判断到有目标
对应图4(a)中阴影部分。信源产生H1假设的样本,在受到噪声干扰后,仍在判决门限右侧,即正确判断到有目标。沿用上文雷达检测导弹例子的描述,即敌方发射的导弹可以被雷达检测到。这部分用P表示,表示正确检测有目标的概率。
5.2情况二:正确判断没有目标
对应图4(b)中阴影部分。信源产生Ho假设的样本,在受到噪声干扰后,仍在判决门限左侧,即正确判断没有目标。沿用上文雷达检测导弹例子的描述,即敌方没有发射导弹,雷达也正确检测到没有目标。这部分用P表示,表示正确检测没有目标的概率。
5.3问题三:错误判断到有目标
对应图4(c)中阴影部分。信源产生Ho假设的样本,在受到噪声干扰后,在判决门限右侧,即错误判断到有目标。沿用上文雷达检测导弹例子的描述,即敌方没有发射导弹,但是雷达却错误地判断成有目标。这种情况被称为“虚警”。这部分用PF表示,表示“虚警”概率。
5.4问题四:错误判断没有目标
对应图4(d)中阴影部分。信源产生Hi假设的样本,在受到噪声干扰后,在判决门限左侧,即错误判断没有目标。沿用上文雷达检测导弹例子的描述,即敌方发射了导弹,但是雷达没有检测到。这种情况被称为“漏警”。这部分用PM表示,表示“漏警”概率。
由图4不难得出四个概率之间的关系:
即正确判断的概率增大时,错误判断的概率降低。
6教学设计:归纳结论
通过课堂讨论与深入探讨,结合板书与图文讲解,可使学生得出以下结论。
6.1结论一:两类错误均不能消除
由图2和图3可以看出,不管判决门限竖直线在横轴上哪个位置“切一刀”,PI、和PM都不会消失。换言之,不管门限定何值,“虚警”概率和“漏警”概率都会存在。通过改变门限,两类错误都不能完全消除。
相关结论可以延伸到其他领域的思考,如医生诊断病人、新冠疫情中的核酸检测等。医生诊断病人对应的“虚警”和“漏警”情况分别为:没患病的被诊断为患病;患病的被诊断为没有患病,即误诊和漏诊。新冠疫情核酸检测对应的“虚警”和“漏警”情况分别为:没有感染新冠病毒的人被检测成阳性:感染新冠病毒的人没有检测出阳性,即伪阳和伪阴。
不管是医生诊断病人时的误诊或漏诊,还是新冠疫情核酸检测中的伪阳或伪阴,都是错误的判决。现实生活中都希望将两者出现的概率降低,采用的方法如多次检测、双门限序列检测等。但是,由上文的分析可以得出,两类错误都会以一定的概率存在,由此可以加深对单个样本有极端可能性的认识。
6.2结论二:改变判决门限需要考虑代价
由图4可以看出,代表判决门限的竖直线向左移动时,Pd和PF变小,P,和PM变大,即正确判断有目标和“漏警”的概率降低:正确判断没有目标和“虚警”的概率增加:代表判决门限的竖直线向右移动时,结果则相反。因此,對于单门限二元检测问题来说,改变门限无法同时降低“虚警”概率P,和“漏警”概率PM。门限降低时,PM降低,但是PF增大;门限提升时,PF降低,但是PM增大。
提出疑问:如何考虑此时门限左移还是右移?引入概念“代价”。两类错误判决都要付出代价,一般情况下,“漏警”和“虚警”的代价是不同的。继续沿用雷达检测导弹的场景例子,此例中“漏警”的代价远高于“虚警”的代价,此时门限应该考虑降低,即将门限左移。
相关结论可以延伸到其他领域的思考,如新冠疫情核酸检测也是“漏警”的代价远高于“虚警”。
7结束语
单门限二元检测问题是最简单的检测问题,信息类专业的学生学习“信号检测与估计”课程是建立数学模型、数学思维的重要环节。其中,课堂教学时长约3学时,经过多次实践,有较好的教学效果。很多专业名词,如“虚警”“漏警”在后续的课程中也继续沿用,通过课堂教学设计,可使学生有深刻的认识和理解。后续课程将在此基础上推导优化准则,如贝叶斯准则、极小化极大准则、奈曼,皮尔逊准则等。相关结论在其他领域的思考可以作为思政元素引导学生,加深对国家政策、社会问题的分析和理解。

