高等数学课程思政教学改革的探索与实践

褚蕾蕾

（西安交通大学数学与统计学院，陕西 西安 710049）

0 引言

2020年6月1日，教育部颁发了《高等学校课程思政建设指导纲要》[1]，提出了课程思政建设是全面提高人才培养质量的重要任务。高数教学实施“课程思政”是一种新的教学改革指向，也是借助高数课程进行思政教育的实践活动，其目标是以“立德树人”为高等数学课程教学的根本任务。“育人为本、德育为先”，将社会主义核心价值观作为课程教学指向，在高等数学课程思政案例中融入政治认同、国家意识、文化自信和公民人格的思政元素，并在高数课堂场景中将案例引入教学实践，以建立渗透德智体美劳知识的教学体系，培养学生正确的世界观、人生观、价值观。实现知识传授、方法启迪、价值引领与情感关怀的统一，将“三全育人”落实到高等数学的教学课程中。这就要求将课程思政融入课堂教学建设的全过程，要让课程思政内容进人才培养方案、进教学大纲、进教案课件、进课堂、进考试，贯穿于教学的各环节，逐步提高课程思政内涵融入课堂教学的水平。教师是高数“课程思政”教学改革的主体，要以课程思政案例设计为抓手，恰当处理高等数学、思政课程、数学文化的关系，选用、设计教学案例，通过案例实现课程功能。

近年来，有学者对高数教学中渗透课程思政元素进行讨论，如吴慧卓[2]，俞能福[3]等。本文在分析高等数学课程存在丰富思政元素的基础上，提出了课程思政融入教学的一种设计方案，并给出教学实践的调查。

1 高等数学课程中存在丰富的思政元素

在高等数学课程教学中，挖掘其思政元素，有如下六大方面可作为思政案例设计的参考。

1.1 微积分课程教学是我国建设工业强国的国家意识的体现

1671—1684年，牛顿和莱布尼茨分别从运动学与几何学中直观的无穷小量出发建立了微积分。随后，1764—1782年，英国的詹姆斯·瓦特在格拉斯哥大学发明并改进了蒸汽机。人类从此进入了工业化时代，微积分学伴随工业化的发展而发展。到20世纪50年代，微积分也是我国工业化的一个重要的数学基础，全国理工科专业均开设高等数学的相关课程，体现了我国工业化的国家意识和对我国发展战略的认同。今天，它仍然服务于我国的现代化建设，并增添了新的广度和深度，这是开设与学习该课程的目的。

1.2 高等数学的本质是认识论问题

首先微积分的研究对象是实数域上连续函数的分析性质，是人们认识物质世界中一些具体事物的抽象，这种抽象概念是人的大脑心智活动，而不是既独立于客观世界又独立于人类思想而存的一个实在，所以，讨论微积分中的概念、理论和方法是一个认识论问题。其二，微积分学的发展是一个由经验认识上升到理论知识的过程，有一个由观察、归纳、算法到理论分析的过程，其过程不是从公理出发经逻辑推理而得，也就是说微积分是应用数学而不是纯数学，尽管公理化方法在描述数学中有重要的应用。其三，既然这是一个应用型的认识论问题，它的源泉就只能是实际问题、实践问题。其四，检验微积分真理性的唯一标准是实践，作为一门数学理论，对它的真理性检验包括逻辑验证、理论检验和应用验证等三个方面。实践是数学认识的源泉与数学真理性的检验标准。

1.3 微积分的基本特征是对立的统一

例如有许多重要的对立概念，如极限的存在性与不存在性，函数的连续性与不连续性，可微与不可微，可积与不可积，二重极限的可交换与不可交换等，其中最基本的是有穷与无穷的对立，在无穷的概念中有潜无穷与实无穷的观点。无理数的发现、无穷小量的提出和实无穷集合论的提出，引起了数学的三次危机，也使其在对立中得以发展，有的还产生新的数学分支。

1.4 数学的无穷观与无穷小量的存在性

在现代科学的描述中，人类所认识的宇宙是普朗克尺度（大约10-35米，10-44秒）上的有限宇宙，而现代数学又描绘了一个与有限物质宇宙完全不同的、无穷的数学世界。极少的数学家采取有穷主义的立场，而大多数则认为自然数是可以构造出来的，且可以一直作下去，这就是潜无穷的观点。— 语言采用潜无穷的观点避开无穷小量的术语建立了精确的极限表述。完备实数系建立在集合论的基础上，是采用实无穷的观点。这就产生了直觉主义学派与形式主义学派的分野。直到1960年前后，鲁宾逊建立非标准实数域才解决了无穷小量的存在性问题，使其在哲学本体论的争论上解决了贝克莱的诘难。高等数学渗透了数学哲学的基本问题。

1.5 数学的文化艺术特征

1872年由德国数学家维尔斯特拉斯构造的处处连续却处处不可微函数，是分析中的重要反例，也是高等数学并不特别关注的“病态”函数。但是，这些反例却成了分形几何思想的源泉，后者提供了数学计算机艺术的分形图形。它们反映出与数学和谐美的另一个奇异性的美感。前者如欧几里得规矩美的和谐，后者如曼德勃罗特分形美的热情奔放。分形就是从奇异中诞生的新颖，这是提升学生文化素养的优良素材。

1.6 数学家的创新精神和优秀品格

在数学的发展历史中，有许多数学家表现出可贵的创新精神、科学素养与优秀的品格，他们积极进取、锲而不舍的治学精神，独立思考、富于创见的治学态度，值得我们学习。他们崇高的家国情怀和使命担当，鼓舞和激励着学生们奋勇前行。

2 高数课程思政的实践探索

2.1 高数课程思政的案例设计

在高等数学思政案例设计中应秉承如下原则。首先要服务于高数课程思政的总任务，体现“品行养成、知识传授、能力培养、思维创新”四位一体的人才培养理念。其二挖掘高数课程的思政元素，使高等数学与思想政治理论课同向同行。其三要注重高等数学“工具性、知识性、科学性、思想性、素养性、文化性”的基本要求，体现高等数学基本的思想方法。其四要选取学生易懂、教师熟悉、便于教学的案例，要有知识性、文化性，不生冷硬拗，有大众化的知识拓展空间，能引起较为广泛的兴趣或深入的讨论，同时设计案例的书写要规范，以体现对案例的理解逻辑。

在案例设计中采用的模板，含案例名称、主题、情景（结合章节、学情分析、教学安排、教学方法）、案例描述（基本描述、问题提出、知识拓展、元素融合）、思政元素及案例反思，后者是教师备课的注记。

2.2 高数课程思政的教学设计

设计六个高数思政案例，可制作为课件，穿插讲授共四个课时，简要介绍如下。

案例1：微积分的产生与思维模式。案例情景：绪论。思政元素：微积分产生于人类的社会实践活动，创新地发明了一种无穷小分析的思维模式。实践是认识的源泉，也是检验真理的标准。

案例2：割圆术与微积分的应用模式。案例情景：逼近的概念。思政元素：认识的过程是由感性认识上升到理性认识；《九章算术》反映了中华文化对数学研究模式的选择，这种模型化、算法化的方法，也是高等数学解决实际问题的模式。

案例3：无穷小量的存在性与数学的无穷观。案例情景：无穷小量的概念。思政元素：通过无穷小量存在性问题的解决，认识到对立统一规律是事物的普遍规律。在人的成长过程中不要惧怕矛盾，要敢于斗争，善于斗争，要有正确的方法去解决矛盾。

案例4：导数计算与数学机械化。案例情景：导数的符号计算。思政元素：通过我国数学家吴文俊在中国古代数学机械化与代数化思想的影响下提出“吴方法”，建立初等几何证明机械化完整体系的实例，增强学生的科学精神与文化自信。

案例5：维尔斯特拉斯函数与数学的分形艺术美。案例情景：可微函数与连续函数的关系。思政元素：数学的艺术美源于数学实践，其形式美依赖于人类生产力的水平；学习科学家的品格与人文精神。

案例6：定积分概念的导入、微元法与数学的认识论方法。案例情景：定积分的概念和微元法。思政元素：通过定积分概念导入中的“分、均、合、精”方法，以及微元法的应用，强调实践对数学方法论的重要性。说明在数学方法上存在演绎、归纳和类比等方法。归纳法也是人工智能的一种方法，归纳与直觉是一种创新性思维。

2.3 高数课程一个思政案例的简要设计

下面给出课程思政案例四“导数计算与数学机械化”的简要设计。通过导数计算的导引，引入数学证明机械化的工具──符号计算软件。机器证明又称自动推理，其基本思想是用一个固定的算法程式去解决一类问题，属于人工智能的领域。初等几何的机械化证明是数学证明机械化的重要例子。1976年底我国数学家吴文俊在中国古代数学机械化与代数化思想的影响下，提出了现称为“吴方法”的奠基性论文[4]，随后又建立了一套求解代数方程组的理论与方法，是求解代数方程组精确解最完整的方法之一，并实现于当前流行的符号计算软件包中。1983年，吴方法被介绍到世界上，并于1997年获得Herbrand自动推理杰出成就奖[5]。吴文俊曾获得2000年首届国家最高科技奖、1956年首届国家自然科学一等奖，体现了崇高的家国情怀和使命担当。

下面，简述吴文俊一个建立初等几何证明机械化的实例。其要点简述如下。

例1用机械化方法证明“平行四边形的两条对角线互相平分”。

Step1将问题表示为代数式。设平行四边形ABCD在平面上的位置如图1所示。其对角线 AC与BD相交于Q。设各点坐标为：

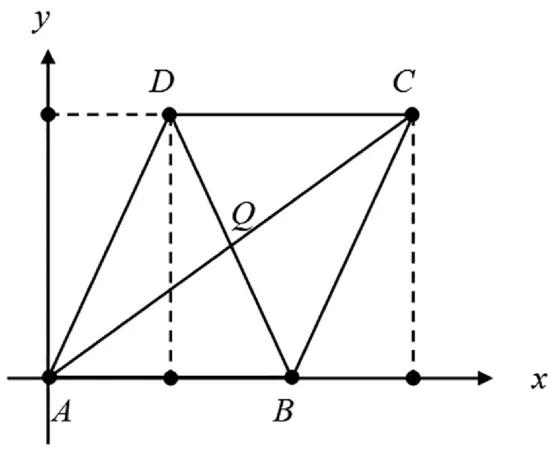
图1

A(0，0)，B(p，0)，C(u，v)，D(x，y)，Q(z，w).

将所设条件用坐标的代数等式来表示。条件DC//AB表示为

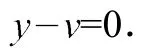
条件AD//BC表示为

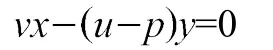
条件点Q在AC上表示为

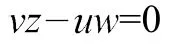
条件点Q在BD上表示为

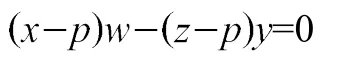
Step2将z、w作为未知量，求解上两式组成的代数方程组，得

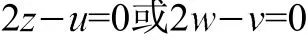
即证明结论|AQ|＝|QC|。由此可得

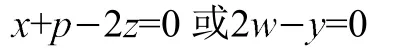
即结论|BQ|＝|QD|成立，完成该命题的证明。

吴方法给两千多年的公理化演绎体系带来了强烈冲击，到20世纪80年代，吴文俊不仅建立了数学机械化证明的基础，而且扩张成广泛的数学机械化纲领，解决了一系列理论及实际问题。吴文俊积极进取、锲而不舍的治学精神,独立思考,富于创见的治学态度，是数学工作者的楷模，是中国数学界的一面旗帜。

2.4 对初步实施高数课程思政的评估

高等数学是大学数学课程及许多专业课程的基础，我校每年有二十多个班同时进行周期一年的教学，面宽量大，内容繁重，是课程思政的一个重要战场。

在今年电类大班的高数教学中初步引入思政案例，调查显示在学生普遍感到课业压力大的情况下，要创新课堂教学模式，关注学生思想动态。学生对课程中增加思政内容是抱有积极态度的，认可品德教育融入高数课程的必要性。将课程思政融入高等数学课，寓价值观引导于知识传授和能力培养之中，起到了帮助学生塑造正确的世界观、人生观和价值观的作用，提高了学生正确认识问题、分析问题和解决问题的能力。在潜移默化中坚定了学生的理想信念，培养了学生探索未知、追求真理、勇攀科学高峰的责任感和使命感，激发了学生的民族文化自信，科技报国的家国情怀和使命担当。从开展课程思政以来，明显看到班上学习风气的改变，擦黑板不用老师催促，上课迟到和打瞌睡的少了，课间打游戏的没有了，学生之间谈论的多数是与学业相关的问题。在和学生的谈话中，感受到满满的正能量，并没有因为课程思政占用了一部分教学时间而影响教学质量。师生互动增多，学生的作业质量和答疑状况比之前都有明显改善，学习成绩也提高了，所以课程思政对高数课程的教学发挥了良好的促进作用。

3 结语

本文在高等数学教学改革中，通过思政元素挖掘、案例设计、课程设计、课件制作等过程进行高数课程思政建设，既是将课程思政融入高数教学的教学，体现“品行养成、知识传授、能力培养、思维创新”四位一体的人才培养理念，又是教师进行课程思政建设的实践性活动，有利于促进教师专业的发展。