零承载传动误差幅值齿轮主动修形设计与分析

蒋进科 方宗德

（1.长安大学汽车学院/汽车运输安全保障技术交通行业重点实验室，陕西西安 710064；2.西北工业大学机电学院，陕西西安 710072）

齿轮承载传动误差反映了轮齿实际啮合与理想啮合的偏差情况，承载传动误差幅值（ALTE）大小是工作过程中振动的直接激励，是产生振动、噪声的重要因素［1-3］，通过齿面承载接触分析（LTCA）可以获得齿轮理论承载传动误差。文献［4-8］借助有限元软件进行LTCA 仿真，其分析结果受有限元网格精度及齿轮副安装精度影响，计算效率较低，主要用于给定齿面的齿轮副传动性能仿真。文献［9-11］根据轮齿啮合过程中的力学平衡条件、载荷当量安装调整值、角位移协调原理、赫兹理论等，按照一定的假设条件对轮齿啮合过程进行数值LTCA模拟，有的侧重力学分析或几何分析，有些研究模型过于繁琐。文献［12］将齿面接触分析（TCA）与有限元法结合起来，针对单对齿轮副提出了一种实用高效的LTCA 数值方法，为本文研究提供了参考。文献［13］在计算时变啮合刚度基础上，推导了承载传动误差的简化公式，并与有限元计算方法对比验证了其正确性。文献［14］基于切片法获得修形斜齿轮的刚度，进一步获得轮齿承载传动误差，该方法不适合复杂齿面及修形齿面。文献［15］中综合Ease-off 拓扑仿真与轮齿刚度非线性单元的耦合解析，给出拓扑修形齿面承载传动误差的计算方法。以上方法都是通过对已知齿面进行LTCA 仿真，获得承载传动误差，然而其无法通过设计啮合位置承载传动误差来逆向设计齿面。

齿轮静态承载传动误差大小与轮齿受载后的实际重合度、几何参数有很大关系，轮齿修形改变齿轮副实际重合度，是减小ALTE 的有效途径［16］。先后出现了二阶、四阶、高阶几何传动误差修形齿面设计［17-20］，其通过预设几何传动误差的形状参数，结合TCA、LTCA、优化算法，进一步降低了ALTE，然而，优化方法很难使ALTE 降为零。同样，文献［21］针对高重合度斜齿轮，基于不同啮合区之间轮齿承载变形规律来预设几何传动误差，进行齿面修形优化设计，尽管可以获得很小的ALTE，但是其修形曲面沿齿向方向呈现周期性波动，且修形量很小，易导致磨齿干涉，在工程应用中难以推广。此外，该方法主要是针对线接触渐开线圆柱齿轮进行修形设计，线接触齿面修形后齿面适配量相对较小，实际重合度主要受轮齿齿间间隙影响，而对于适配量较大的复杂局部共轭齿面，其实际重合度受齿间间隙与齿面法向间隙二者共同影响，因此，该方法未必适合。文献［22-23］表明优化静态ALTE 未必降低振动，ALTE 降低后也易导致传动误差曲线中高频成分增加，产生新的振动。

综上所述，为了有效降低某具体工况振动，需要研究可加工的零ALTE 齿轮的修形设计与制造方法。为此，针对平行轴渐开线圆柱齿轮，结合TCA、LTCA 数值方法提出一种基于零ALTE 的新LTCA 方法。该方法通过对啮合位置同时啮合齿对的齿间间隙进行补偿，消除不同啮合位置轮齿承载变形的差异；通过对齿面不同啮合位置补偿间隙的约束，可获得光滑的修形齿面，避免了齿面修形量的周期性波动，为进一步的高性能齿面减振设计与分析提供理论参考。

1 预设修形齿面建模

齿轮副的齿面初始接触间隙即几何特性表示为接触线法向间隙和齿间间隙之和，可通过TCA方法获得。齿间间隙主要影响轮齿动态特性，接触线法向间隙主要影响轮齿接触区的大小、位置，进一步影响轮齿强度及动态特性。齿面修形是对轮齿微观几何的修正，需要结合齿间间隙与齿面法向间隙产生的机理进行修形设计。修形齿面表达不能脱离理论齿面，数字化齿面进行TCA分析时，计算过程中迭代太多，计算效率较低，因此，修形齿面需要有确定的解析表达式。通过共轭齿面和齿面初始接触间隙所映射的法向修形曲面的叠加，可以灵活、解析地表达复杂修形齿面。修形齿轮副齿间间隙的大小表示为图1（a）所示抛物线几何传动误差曲线Ψ的函数，将啮合点M0处几何传动误差乘以该点位矢rf在法矢nf方向的投影半径，可得到接触齿对的齿间间隙，根据函数Ψ的参数ε1、λ0可设计齿间间隙。如图1（b）所示，根据啮合点M0处rf、nf计算瞬时接触椭圆长轴上点Mj处的位矢，过Mj点平行于nf的直线与两齿面的交点Mj1和Mj2之间的距离即为齿对的接触线法向间隙；根据图1（c）的修形量分段抛物线函数ζ的参数d1、d2、q1、q2可设计接触线的法向间隙。渐开线斜齿轮齿面的齿廓、齿向、拓扑修形实际是综合了齿间间隙、接触线法向间隙的齿面微观几何设计，其设计思路见文献［24］。

图1 齿轮修形曲线Fig.1 Curves of modified gear

2 零承载传动误差幅值齿轮副齿间间隙补偿量确定

文中主要是对齿轮副的齿间间隙进行补偿，关于接触线法向间隙的补偿方法更为复杂，暂不予讨论。基于零ALTE 的齿轮副齿面补偿间隙计算原理为：结合原LTCA 方法，获得轮齿啮合位置最大承载变形量，通过对共轭或预设修形齿轮一个啮合周期初始齿间间隙补偿，使补偿后的承载变形等于该最大变形量，通过改进原LTCA 方程的求解算法反求出该补偿间隙。为了便于加工修形齿面，该补偿间隙大小需要根据齿面啮合位置进行约束，保证啮入或啮出位置的补偿间隙较大，并减少补偿间隙的周期性波动。原LTCA 技术原理为将TCA 与有限元法结合起来，根据啮合位置的多齿对初始间隙，将齿轮副受力接触转化为求解齿面有限个离散接触点的力学平衡问题，其数学模型如图2所示。

图2 齿轮LTCA模型Fig.2 LTCA model for gears

在载荷P作用下，某瞬时有两对齿接触并发生弹性变形，设小轮固定，大轮沿法向运动Z。忽略齿面摩擦且假设轮齿沿瞬时接触方向发生线接触，齿面接触描述如下：

式中：pjk（j=1，2，…，n）、djk（j=1，2，…，n）为齿对k的沿瞬时接触线方向离散点j处的法向载荷、变形后的轮齿间隙，pk、dk为其离散点组成的向量；Fk为齿对k的接触离散点组成的法向柔度向量，通过有限元计算得到；wk为齿对k离散点初始接触间隙组成的向量，通过TCA计算得到。上式是由已知参数F、P、W和未知参数p、Z、d组成的一个非线性规划，求解后可得到未知参数，将Z转化为啮合线上的位移，用转角表示即为一个啮合周期的承载传动误差。Z是有限元解，包含轮齿受力弯曲变形及接触变形。

一个啮合周期的各个啮合位置由于轮齿接触间隙和啮合刚度的不同而得到不同的Z，构成了承载传动误差曲线。欲使ALTE 为零，必须使各啮合位置的Z相同；而上面LTCA 方法只能正向输入W求解Z，无法通过输入相同的Z逆向求解啮合位置的W。逆向求解的间隙实际是对原初始间隙的修正，其可以表示为原初始间隙与补偿间隙的和，为了获得该补偿间隙，需要重新构造LTCA 方程，同时对求解算法进行改进。

假设接触位置的补偿初始间隙ejk（j=1，2，…，n）增大（ejk≥0），其组成向量为ek，则补偿后承载变形始终会大于等于补偿前最大承载变形，这里主要补偿齿间间隙，则新LTCA位移协调方程为

理论上式（2）存在多个解，e受齿面补偿位置、补偿量大小影响，且齿面各啮合位置的补偿间隙可以有多种组合。例如，一个啮合周期分成8（k=1，2，…，8）等份，齿面总计21个接触位置，主要补偿靠近啮入端第1～8 位置或啮出端第17～21 或中间第9～16 位置的间隙，其他位置补偿量通过约束与主补偿位置产生函数关系。考虑到齿对的多齿接触特性，当k=1 时应补偿的是第1、9、17 个接触位置，以靠近啮入端第1 个接触位置为主补偿，第9、17个位置通过权系数a11、a21约束，鉴于中间位置的补偿量a11易导致内凹，因此其取值小于0.3，啮出端a21系数可以稍大于0.3即

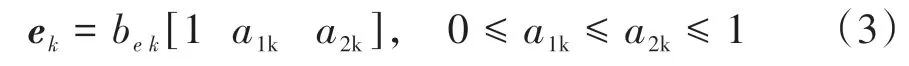
式（2）、（3）及（1）中的力平衡条件、非嵌入条件构成新的LTCA 方程组，其是由已知参数F、P、W、Z和未知参数p、d、e组成的一个非线性规划，通过对原LTCA求解算法的改进可以反求出未知参数。附加齿间间隙e叠加于原预设的修形齿面即为零ALTE齿轮副的修形齿面。e的大小及其拟合曲面形状影响修形齿面的加工难易程度，理想的附加齿间间隙应是从齿面啮入至啮出呈抛物线形状、非周期性且不易太小，便于通过平面砂轮线接触或锥面砂轮点接触数控磨齿实现齿面高阶修正。e转化为啮合线上角位移，可得到不同啮合位置的附加几何传动误差Te（单位″）为

式中：Rb2、β分别为被动大轮基圆半径和螺旋角。轮齿综合刚度表示为

3 零承载传动误差幅值修形齿面确定

上面方法确定了齿轮副有限个接触位置的附加几何传动误差，采用三次均匀B 样条对其进行拟合，则整个啮合过程中附加几何传动误差为

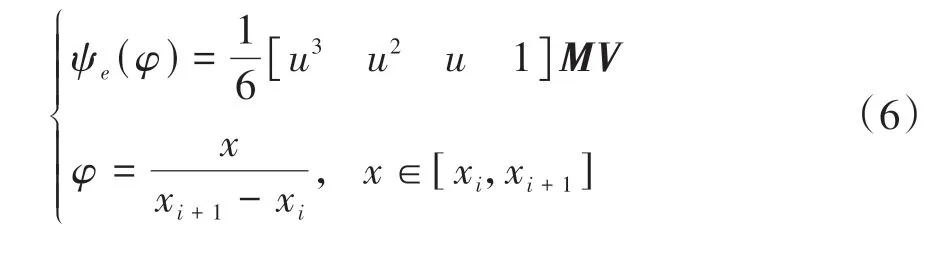
式中：xi为小轮转角，Vi为齿面接触点补偿几何传动误差型值的控制点列向量，i=1，…，n-1；M为常量矩阵。至此整个啮合过程中零ALTE 齿面的主动轮转角φ1与被动轮转角φ2的关系表示为

式中：z1、z2为主、被动轮齿数；φ10、φ20为主、被动轮初始转角。根据齿面啮合原理，将大轮齿面视为假想齿轮刀具，按照式（7）传动比关系展成小轮，可确定零ALTE 的小轮修形齿面位矢r1、法矢n1；假设修形均放在小轮上，则零ALTE 小轮法向修形量为

式中：r1t、n1t分别为小轮渐开线齿面位矢、单位法矢，u、l为齿面参数。零ALTE 修形齿面的设计过中仅需要3 次LTCA 计算，其中第1、3 次采用原LTCA正向算法对第2次的新LTCA算法进行辅助计算和验证，整个计算过程仅需1 min左右。

第1 次原LTCA 仿真中输入数据为预设修形齿面的初始接触间隙，主要获得啮合周期的最大承载变形量Zmax；第2次新LTCA仿真，输入参数为预设修形齿面的初始接触间隙与Zmax（各啮位置均相等），通过逆向求解获得各啮合位置的补偿修形量，并对其插值获得整个啮合过程中的补偿修形量，进一步获得零ALTE修形齿面，但是插值会有一定的误差，因此需要对插值后的齿面重新进行第3 次正向LTCA 计算。输入参数为零ALTE 修形齿面TCA 计算的初始接触间隙，其意义是进一步验证逆LTCA算法及插值获得的零ALTE 齿面精度的有效性。具体流程如图3所示。

图3 零ALTE修形齿面主动设计流程Fig.3 Flow chart of active design tooth surface for Zero ALTE modification gears

4 数值仿真与分析

以表1、表2 所示的直、斜齿轮副为例，针对具体工况、不同重合度齿轮副的零ALTE 齿面的主动修形设计与分析如下。

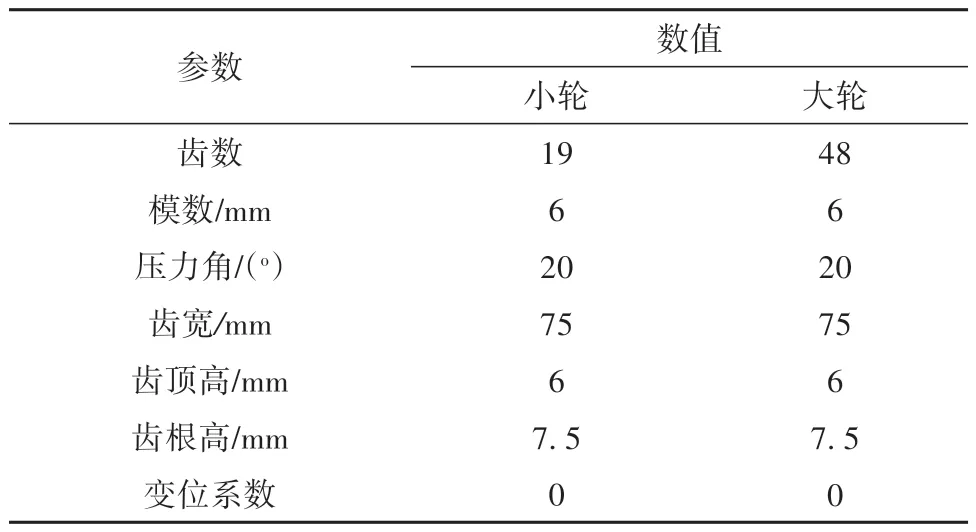
表1 直齿齿轮副参数Table1 Parameters of spur gear pair

表2 斜齿齿轮副参数Table 2 Parameters of helical gear pair

（1）基于LTCA 数值方法的承载变形仿真精度验证。文中LTCA 方法的仿真精度受齿面柔度系数插值精度影响即受瞬时接触线离散点个数的影响。为了验证LTCA 方法的正确性，鉴于直齿轮综合啮合刚度的计算方法已通过了试验并制定了相应标准，这里以表1所示直齿轮副为例，按照GT 3480.1—2019计算公式进行比对。GB 计算公式是根据实心盘状齿轮测量获得，对于低载荷工况（单位齿宽载荷<300 N/mm）是通过理论修正系数（取值0.8～1.0）进行调整的，这里取大轮扭矩5 000 N·m 属于高载荷工况，因此，该公式中的计算数值不进行修正，即理论修正系数取1.0。LTCA 方法中，材料的杨氏模量E=206 GPa，泊松比=0.3，齿轮有限元网格模型采用20节点等参单元，精度高于相同体积下的8节点六面体单元模型，并根据齿宽和模数比值，沿齿向方向的网格个数进行了自适应加密，可以满足计算精度要求。这里齿轮柔度系数的计算采用有限元网格个数在齿高、齿向均为6及双线性插值获得接触线离散点的柔度系数。瞬时接触线均匀离散点个数分别为5、7时，二者的计算结果如图4所示，可见LTCA 方法与GB 方法结果较为接近，特别是接触线离散点为7 个时结果一致，主要原因是LTCA方法中有限元网格中齿向为6个单元，此时插值点位置离网格型值点最近，插值精度较高。

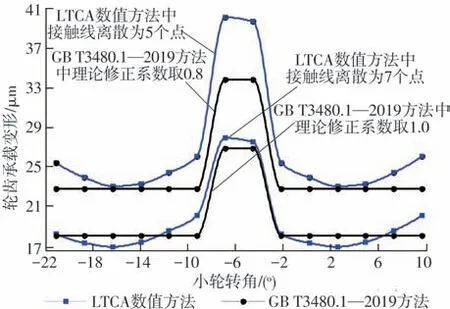
图4 直齿轮承载变形算法对比Fig.4 Comparison of load deformation algorithms for spur gears

（2）基于预设几何传动误差的直齿轮零ALTE齿面仿真。针对仅预设抛物线几何传动误差，即齿廓修形直齿轮，分别在2 000 N·m 及4 000 N·m 工况进行零ALTE 齿面1及零ALTE 齿面2的设计。一个啮合周期分为8等份，一个齿从啮入至啮出接触位置（小轮齿根至齿顶）总计13个，其中第6至8接触位置为单齿啮合区，主要对靠近啮入端的第1至8 个啮合位置进行间隙补偿，补偿间隙及几何传动误差见图5（a）。预设修形齿面的第8个位置承载变形最大，显然零ALTE 齿面1 的补偿间隙大小与未补偿前的承载变形大小变化规律相反，即承载变形越大，补偿间隙越小，这与物理模型规律是一致的（如图5（b）所示）。零ALTE齿面1接触印痕良好、几何传动误差无明显内凹现象（如图5（c）所示）；随载荷变化轮齿承载传动误差增加（如图5（d）所示）；预设修形齿面在2 000、4 000 N·m 工况下ALTE 分别为0.000 6°、0.003 5°，而补偿后的齿面（零ALTE齿面1、零ALTE齿面2）ALTE值为6.4×10-8°、4.2×10-7°（即为0），可见附加间隙的拟合误差对ALTE无影响（如图5（e）所示）。零ALTE 齿面1的修形量较光滑，整体呈现凸状，相对标准齿面其附加展成位移仅较预设修形齿面在啮入端略有变化，但整体上还是接近抛物线形状，便于加工；而零ALTE齿面2的修形量较大，主要是因为4 000 N·m工况下预设修形齿面的承载变形差异较大导致（如图5（f），5（g），5（h），5（i）所示）。因此，预设的修形量、载荷对零ALTE 齿面补偿修形量及加工难易程度有一定的影响。

图5 基于预设几何传动误差的直齿轮零ALTE齿面设计与分析Fig.5 Tooth design and analysis for spur gear with zero ALTE based on preset geometric transmission error

（3）对角修形斜齿轮零ALTE 齿面仿真。仅预设几何传动误差的方法进行的斜齿轮修形可实现一种对角修形齿面。斜齿轮重合度较大，同时啮合齿对可超过3个，补偿修形量的位置更为灵活，可以有多种组合。为了研究补偿间隙大小、曲线形状与齿面主要补偿位置的关系，针对同一预设几何传动误差斜齿轮进行补偿修形设计，预设修形量见图6（a）。预设修形齿面TCA 仿真见图6（b），较大几何传动误差可以减小安装误差敏感性，齿面接触位置总计21 个，这种对角修形对齿面印痕影响较小，类似直齿轮齿廓修形。负载3 000 N·m 工况下承载变形如图6（c）所示，预设修形后的ALTE 减小近50%，啮合周期内其变化先减小后增大，对预设修形齿面进行4 种不同类型补偿修形，其中零ALTE 齿面2、零ALTE 齿面3、零ALTE 齿面4依次补偿靠近啮入端的第1～8个位置、啮出端第17～21个位置、中间部分的第9～16 个位置，ALTE 齿面1综合啮入端及啮出端位置进行补偿。补偿后的齿面即零ALTE 齿面1、零ALTE 齿面2、零ALTE 齿面3、零ALTE 齿面4 的ALTE 值分 别 为2.50×10-5°、2.5×10-5°、2.6×10-5°、2.6×10-5°，分别接近0，较共轭齿面减小了98%，图中仅给出零ALTE 齿面4的承载传动误差。附加间隙的拟合误差对承载传动误差基本无影响（4 种补偿修形的ALTE 曲线基本重合）。补偿修形量转化为几何传动误差如图6（d）所示，分析如下。

①主要补偿齿面中部时，补偿间隙量最小，且出现较小的中凹现象，补偿量变化与预设修形齿面的ALTE 变化规律基本相反，主要原因是预设修形齿面中部的修形量基本无变化，主要补偿的是啮合位置承载变形之间的差异。②主要补偿啮出端时，补偿量最大且在啮合位置21 处，其原因是同时啮合齿对即齿面接触位置5 处的预设初始间隙较小；因主补偿位置17～21 总计5 个，必然要引起同时啮合齿对第1～5个位置的补偿量变化。③主要补偿啮入端时，同样，补偿量变化与预设修形齿面的ALTE 变化规律基本相反，但其较补偿中部时的数值大，原因是不仅要补偿承载变形差异，还要补偿啮合位置初始接触间隙（预设修形量）之间的差异。可见补偿间隙曲线形状受啮合位置及其预设初始接触间隙的影响，且不同类型中齿面基本都存在一段补偿量，其特征为变化规律与轮齿承载变形变化规律相反。④部分零ALTE齿面修形曲面见图6（e），6（f），6（g）所示，曲面无较大内凹，可见合理的附加齿间间隙基本能很好融合于预设修形齿面。

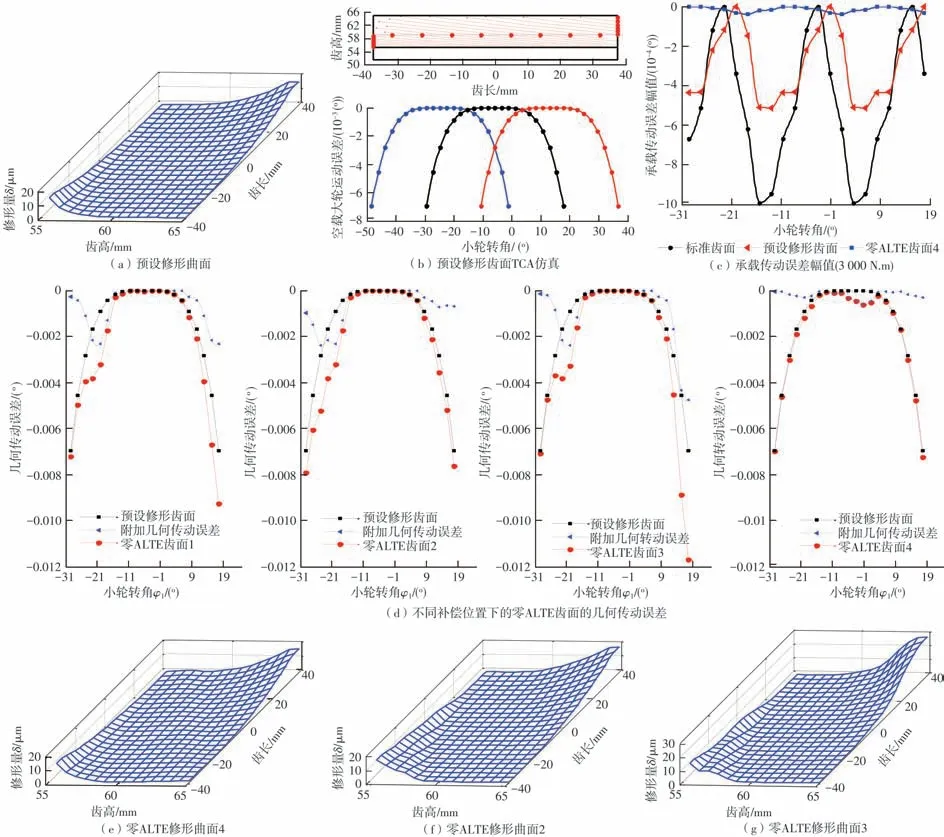
图6 基于预设几何传动误差的斜齿轮零ALTE齿面附加齿间间隙仿真Fig.6 Simulation of additional tooth clearance for helical gear with zero ALTE based on preset geometric transmission error

文中的齿面附加修形量是根据附加几何传动误差得到的，其特点是修形量沿轮齿瞬时接触方向相等，而齿条刀具（例如大平面砂轮）与工件接触时正是沿着这条瞬时接触线切削，当几何传动误差无较大内凹或呈现抛物线形状，该方向上平面砂轮的曲率始终小于轮齿接触线主曲率，且砂轮的展成运动曲线与传动误差曲线的形状一致，因此不发生干涉，可通过改变滚比在多轴数控机床上实现砂轮磨齿加工，具体见文献［25］.

（4）基于预设拓扑修形的斜齿轮零ALTE 齿面仿真。预设几何传动误差的修形齿面适用于航空高速薄壁结构斜齿轮的修形。实际中拓扑修形斜齿轮应用更为广泛，针对同一种预设拓扑修形齿面进行补偿，其预设修形曲面见图7（a）。零ALTE 齿面1主要补偿中间部分的第9～16个位置，零ALTE齿面2主要综合啮入端及啮出端位置进行补偿，计算得到的最大补偿量分别为3、5 μm，该补偿量可以很好地融合于预设修形齿面（即零ALTE齿面的修形量趋于光滑，且无较大内凹）如图7（b），7（c）所示，理论上可通过点接触磨齿实现该齿面加工。基于齿间间隙的补偿量不改变齿面接触印痕，仅改变齿轮副的几何传动误差（如图7（d），7（e）所示）。针对3 000 N·m 工况下补偿修形后的零ALTE 齿面1、零ALTE 齿面2、零ALTE 齿面3 的ALTE 分别为5.3×10-5°、4.7×10-5°、4.0×10-5°即接近0，较共轭齿面减小了97%。随载荷增加，补偿修形后ALTE先从某值减小至零，此时载荷（3 000 N·m）作用下齿间间隙并未完全消除，随载荷的增加承载变形并非接近线性增加，而是缓慢增加，相比前面的修形方式在更宽载荷范围降低了ALTE（如图7（f）所示）。

图7 基于预设拓扑修形的零ALTE齿面修形设计Fig.7 Tooth design for helical gears with zero ALTE based on preset topology modification

需要说明的是文中LTCA 模型忽略了齿距误差影响，主要适用于高精度齿轮副。文献［25］中针对不同类型相对基节误差下的LTCA 研究表明：相对基节误差在不同程度上放大了啮合位置的承载变形，相邻齿对的相对基节误差幅值越大，ALTE 越大。因此，当齿对存在相对基节误差时，本文的方法在降低ALTE 方面仍有一定的改善作用。此外，齿轮副齿数互质使得齿对相对基节误差随机性很大，因此，整个传动过程中零ALTE 很难实现；在本文研究基础上通过智能算法总结整个传动过程中相对基节误差与ALTE 的关系，并进行预估，可确定更合理的补偿修形方式，为下一步的齿轮传动全过程中ALTE最小奠定基础。

此外，当具体载荷工况ALTE 减小为零时，临近具体载荷工况的ALTE 也有可观的改善，理论上修形渐开线齿轮副不可能实现多个载荷下ALTE 为零。追求更宽载荷范围下ALTE 最小，则需要进一步研究基于拓扑修形零ALTE设计方法。

5 结语

建立零ALTE齿轮LTCA数值新方法，该方法按照预设修形齿面的LTCA分析获得承载变形最大值，以啮合周期的承载变形量与该最大值相等为已知条件，建立新LTCA 方程，并反求啮合位置的附加修形量，该修形量特点是沿瞬时接触线相等，且叠加于原预设修形齿面即为零ALTE齿面。主要结论为：

1）零ALTE 齿面的补偿修形量大小、曲线形状与齿面主要补偿位置、预设修形量、载荷有关；

2）当啮合周期内补偿位置的预设修形量变化较小时，补偿量变化与预设修形齿面的ALTE 变化规律基本相反，即承载变形越大，补偿间隙越小；实际补偿的是承载变形差异，整体补偿量较小；

3）当啮合周期内补偿位置的预设修形量变化较大时，整体补偿量也较大，原因是不仅要补偿承载变形差异，还要补偿啮合位置初始接触间隙（预设修形量）之间的差异；

4）合理的补偿位置与预设修形量，可使补偿量很好地融合于预设的修形齿面，即零ALTE 齿面的修形量趋于光滑、无较大内凹，便于ALTE 齿面加工；

5）基于预设拓扑修形齿面的零ALTE 修形齿面，当ALTE 减小为零后，随载荷的增加承载变形缓慢增加，可在更宽载荷范围降低ALTE；

6）文中讨论了基于齿间间隙补偿方法的齿面修形设计，可应用于各种齿轮副，而对于接触线法向间隙的补偿方法及综合二者的补偿方法需要进一步讨论。