基于扰动卡尔曼滤波的机器人免力矩传感器拖动示教方法
张铁 许锦盛 邹焱飚
(华南理工大学机械与汽车工程学院,广东广州 510640)
拖动示教不需要编程基础,操作简便且效率高,更适合于现代化的柔性生产。而目前具有拖动示教功能的机器人一般为关节内部集成了力矩传感器的DLR 机器人[1]和配备了双编码器的UR 机器人[2],其通过力矩传感器或双编码器来直接测量关节外力矩,从而基于柔性控制来实现拖动示教功能。但是在实际情况中,工业机器人的关节内一般只具有单编码器且没有集成力矩传感器,所以免力矩传感器的拖动示教对于工业机器人来说存在挑战。实现免力矩传感器拖动示教的关键问题是能够准确地对外力矩进行观测,并对关节驱动力矩进行高精度控制。
根据机器人的动力学模型和运动状态来估计外力是实现免力矩传感器测量外力矩的常用方法,其中动力学模型是影响外力矩估计精度的重要因素。文献[3]中分别辨识关节端与电机端的动力学方程,其中电机端采用了Lugre 动态摩擦模型,然后将两者计算的关节力矩差值作为估计的外力矩,但这种方法需要建立复杂的摩擦模型且增加了模型辨识的难度。文献[4-5]中通过引入广义动量,将动力学模型转化为不含加速度的形式,去除了加速度的噪声干扰,进而将广义动量的残差量作为观测量,实现了外力矩的迭代估计,但基于广义动量的外力估计法并没有考虑到动力学模型的辨识误差等影响,且估计精度受观测矩阵所限制。文献[6-7]中进一步将广义动量与扰动观测器相结合,基于卡尔曼滤波算法对外力矩进行估计,提高了外力矩估计的精度。由于卡尔曼滤波算法能够实时调整由模型误差所引入的过程噪声与由测量误差而引入的测量噪声,所以其具有更高的估计精度与更好的鲁棒性。
拖动示教的控制方法通常分为基于力矩和位置模式的控制方法。文献[8]中设计了基于自测量的重力矩与摩擦力矩的计算方案,对机器人示教过程中的重力与摩擦力进行力矩补偿,从而实现了轻型机器人上的拖动示教;文献[9]中将实时补偿的重力与摩擦力转换为目标电流值,并直接加在电流控制环上,提高了拖动示教的速度响应。但基于力矩模式的控制方法对外力比较敏感,容易造成系统的不稳定。文献[10]中通过实时补偿重力、摩擦力与惯性力,建立了机器人的平衡状态,然后在该状态下计算由外力引起的关节转角,从而基于位置控制环实现机器人的拖动示教,但该方法在位置外环上的计算比较复杂且需要知道精确的PD 控制常数。文献[11]中首次提出阻抗与导纳控制的概念,其通过调节机器人末端力与环境之间的质量阻尼弹簧系统,以实现两者之间的良好交互性。文献[12]中使用导纳控制算法将外力转换为示教运动的期望位置,并将高频抖动力矩[13]与补偿的重力、摩擦力作为前馈力矩,两者协同控制机器人完成拖动示教。导纳控制通过位置规划来动态调整人机交互中外力与位置偏移量之间的动态关系,稳定性高,所以更适用于机器人的拖动示教控制中。
本文中提出以刚体动力学模型与深度神经网络相结合的方式来建立机器人的动力学模型,其中深度神经网络以刚体动力学模型的力矩残差为训练目标进行离线训练,进一步补偿模型的误差。考虑到辨识误差与测量噪声,本文基于扰动卡尔曼滤波算法对机器人的关节外力矩进行估计,并提出一种自适应阻尼的导纳控制方法来实现机器人的拖动示教,以改善启停时的示教效果。
1 基于扰动卡尔曼滤波的机器人外力矩估计方法
1.1 基于深度神经网络的机器人动力学模型
扰动卡尔曼滤波算法是一种基于模型的最优估计方法,所以动力学模型的精度很大程度上影响了外力矩的估计精度,因此提出以刚体动力学模型与深度神经网络相结合的方式来共同建立机器人的动力学模型。
机器人的刚体动力学模型可表示为
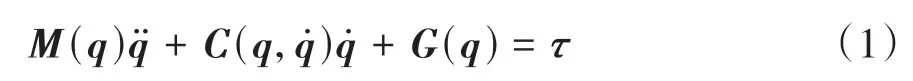
式(1)的模型可通过整体实验辨识法[14]进行辨识,因此得到计算的关节力矩为
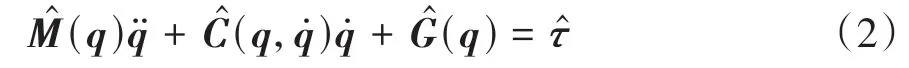
在实际情况下,实际力矩与式(2)的计算力矩会存在偏差,将其定义为关节力矩残差,

式中,ε表示关节力矩残差,ε∈Rn。
存在力矩残差的原因为式(1)描述的动力学模型并不全面,在实际情况下关节内部还有摩擦和耦合等现象,由这些现象引起的关节力矩在现有方法下很难进行精确的建模[15]。所以提出使用深度神经网络来对关节力矩残差进行黑箱建模,该方法不对具体的函数关系进行推导,而只学习网络输入与力矩残差之间的映射关系,从而避免复杂的建模过程,同时也能将其他的建模误差补偿到网络中。
在一组激励轨迹数据下,机器人第一关节的力矩残差ε1与关节速度的关系如图1所示。可以发现力矩残差与关节速度之间存在一个隐含的映射关系,而这种关系一般是未知的,建立深度神经网络的目的就是通过训练使网络学习这种映射关系,从而基于可测量的关节转角、速度与加速度来计算得到力矩残差。因此,本文为机器人的各个关节单独建立一个全连接深度神经网络,如图2所示,其中下标i=1,2,…,n表示机器人的关节i的含义。网络的输入层为3个神经元,分别对应关节i的转角、速度与加速度,输出层为一个神经元,对应关节i的力矩残差εi。在建立的深度神经网络中,全连接层的作用为改变网络层的维度以提高网络的映射能力;随机失活层加在全连接层后,在每轮训练时,全连接层的神经元会以概率p随机失活,以防止神经网络出现过拟合,提升网络的泛化能力;Leakly Relu激活函数层是神经网络学习非线性映射关系的基础,能有效防止深度神经网络出现梯度消失的现象。
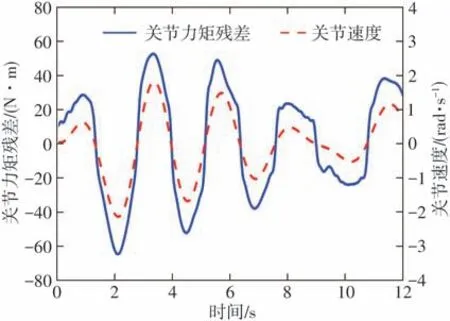
图1 关节力矩残差与关节速度的关系Fig.1 Relationship between joint torque residual and velocity

图2 全连接深度神经网络的框架Fig.2 Framework of fully connected deep neural network
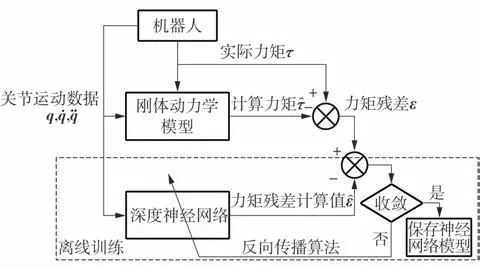
图3 深度神经网络的训练框架Fig.3 Training framework of deep neural networks
在式(1)的基础上添加训练后的深度神经网络的输出,由此完善原来的刚体动力学模型,减少模型误差。因此,基于深度神经网络的动力学模型为
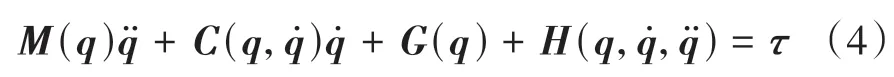
1.2 机器人动力学模型的状态空间表达式
在拖动示教下,机器人的外力矩向量可看成是机器人系统外的一种扰动,所以根据经典的扰动观测器原理[16],外力矩模型定义为

式中:τe为关节外力矩向量,τe∈Rn;Ae为表示外力矩变化趋势的对角矩阵,Ae∈Rn×n;外力矩模型误差ωe定义为高斯噪声ωe~N (0,Qc,e),Qc,e为其协方差对角矩阵,Qc,e∈Rn×n。
在关节外力矩影响下,完整的动力学模型为
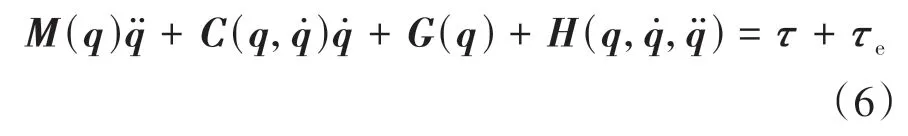
通过组合关节外力矩与广义动量为系统状态变量,将式(6)转化为状态空间表达式,进而能够基于卡尔曼滤波算法对关节外力矩进行最优估计。
引入机器人的广义动量为


结合式(6)-(8),式(6)可表示为

式中:符号τu定义为式(10)以简化表示;辨识误差ωp为辨识项而引入的误差,定义为高斯噪声ωp~N (0,Qc,p);Qc,p为其协方差对角矩阵,Qc,p∈Rn×n。

结合式(5)-(9),将关节外力矩与广义动量组合为状态变量,并定义广义动量为状态空间的输出,机器人动力学模型式(6)可表述为状态空间的形式:

在式(11)中:系统状态为x=[pT,τeT]T;系统输入为u=τu;系统状态转移矩阵A、输入矩阵B与输出矩阵C分别为
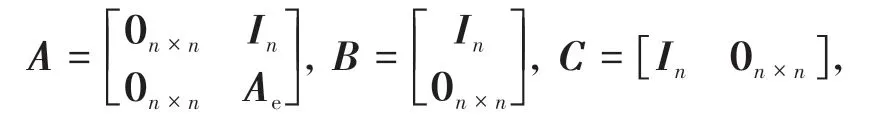
式中,In为单位矩阵,In∈Rn×n。系统过程噪声ω表示为,即,

由于关节转角与速度是可测量的,所以系统的输出y定义为可测量的广义动量p。测量噪声v定义为高斯噪声v~N (0,Rc),其包括了测量关节转角与速度时引入的噪声。由于关节速度是基于关节转角进行微分而获得的,而微分计算会放大噪声的影响,所以关节速度的噪声是测量噪声的主导因素。因此协方差矩阵Rc定义为

1.3 基于卡尔曼滤波算法的外力观测器
基于式(11),采用卡尔曼滤波算法对系统状态x进行最优估计,从而根据系统的最优状态得到外力矩的观测值。由于卡尔曼滤波是一种递推型的算法,所以对式(11)进行离散化,
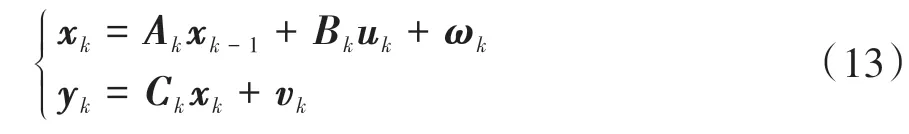
式中,k为离散系统的时间变量。离散系统下的系统矩阵Ak,Bk可通过矩阵指数[17]来计算获得:
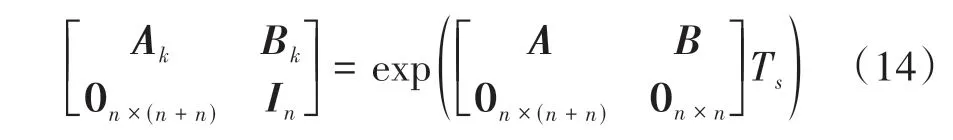
式中,Ts为系统的采样周期,exp(⋅)表示矩阵指数。
输出矩阵Ck与测量噪声vk的协方差矩阵Rk更新方式为

过程噪声ωk的协方差矩阵Qk通过式(16)-(18)计算得到:
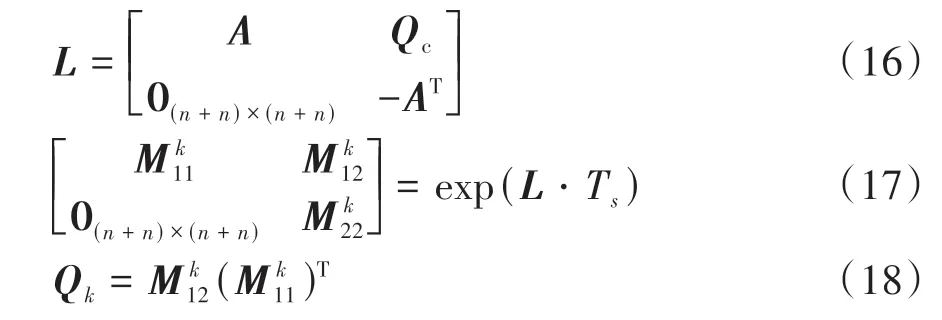
因此,对于离散后的式(13),基于扰动卡尔曼滤波的外力矩估算法可概括为如下算法1。

2 机器人免力矩传感器拖动示教的控制方案
基于扰动卡尔曼滤波算法对机器人外力矩进行最优估计后,通过所提出的自适应阻尼的导纳控制方法将外力矩转换为示教运动的目标指令,从而实现拖动示教的控制。
在关节空间中完整的导纳控制算法为,

式中,Md、Dd、Kd∈Rn×n分别为系统的惯性矩阵、阻尼矩阵与刚度矩阵,它们都为对角矩阵且对角线上的元素分别表示各个关节的惯性参数、阻尼参数与刚度参数。qd为示教运动的期望关节转角向量,qd∈Rn;qr为参考轨迹的关节转角向量,qr∈Rn。
式(19)的输入为外力矩τe,输出为期望的关节转角qd,其控制的目标是维护由外力矩而产生的位置偏移量qd-qr和外力矩τe始终保持式(19)所述的二阶阻抗模型,从而使机器人关节能够随着外力矩作用而运动。因为拖动示教是在可行范围内进行拖拽运动的,参考轨迹定义为所以对于一维的关节i,式(19)表示为

式中,下标i=1,2,…,n表示机器人的关节i的含义。
将式(20)进行离散化,并基于积分迭代法对期望关节加速度进行积分,从而得到在离散系统下期望关节速度与关节转角的更新方程为

由式(22)看出,系统惯性参数与阻尼参数是影响示教运动效果的主要因素。系统惯性参数主要影响示教运动的稳定性,设定后一般不随意更改;系统阻尼参数影响示教运动跟随外力矩变化的响应速度。为了改善机器人在示教启停阶段的拖动效果,提出了一种阻尼参数自适应调整的方法,

式中:Dsti为系统阻尼参数的一个标准值;α>0为控制外力矩变化率的一个参数;sign(⋅)为符号函数,主要作用为区分正反方向运动时阻尼参数自适应调整的方向;为外力矩变化率,

式中,m>1 为微分间隔常数,以减轻微分所引入的高频噪声影响。
由式(23)看出,在示教的启动阶段,外力矩变化率的方向与外力矩τei的方向相同,阻尼参数Ddi随外力矩变化率的增大而减小,示教运动的关节转角qdi因此增大,从而利于操作者能以较小的力轻松拖动机器人;在示教的停止阶段,外力矩变化率的方向与外力矩τei的方向相反,阻尼参数随之逐渐增大,期望关节转角qdi因此减小,从而有利于机器人的快速停止。
综上所述,机器人免力矩传感器拖动示教的控制方案如图4所示,在每一个控制周期下,根据机器人反馈的关节转角、速度与加速度信号,基于扰动卡尔曼滤波算法对机器人关节外力矩进行最优观测;系统阻尼参数基于式(23)进行自适应调整,进而由式(21)-(22)计算出示教运动的期望关节转角;然后将该运动指令下发到机器人的伺服控制器中,机器人通过自身的位置闭环控制来跟踪该运动指令,从而实现机器人的拖动示教。
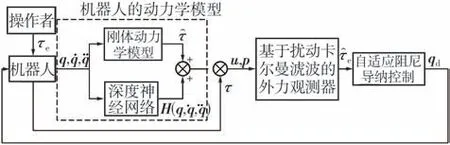
图4 机器人拖动示教控制方案Fig.4 Control scheme of robotic drag teaching
3 实验结果与分析
3.1 机器人实验平台
使用GSK RB08A3的六轴机器人作为实验机器人,实验平台如图5所示。当运行时,机器人能实时地返回各关节的位置编码器与电机电流信号,从而通过对应的函数关系将信号转换得到关节转角、速度与驱动力矩信息。上位机根据反馈信号计算控制指令,然后通过控制柜产生驱动信号来驱动机器人进行运动。机器人系统的控制周期为1 ms。

图5 机器人实验平台Fig.5 Robot experimental platform
3.2 基于深度神经网络的机器人动力学模型辨识实验
首先通过SymPyBotics 工具箱[18]建立机器人的刚体动力学模型,然后将周期性傅里叶级数作为激励轨迹[19],采用巴特沃斯低通滤波器对采样信号进行低通滤波,最后基于加权最小二乘法完成刚体动力学模型的辨识,该部分辨识方法具体可参照文献[20]。
如图3 所示,在PyTorch 的深度学习框架下对深度神经网络进行训练。训练集数据中的从滤波后的激励轨迹数据中获得,ε则由式(3)计算得到。训练集样本选为10 组激励轨迹的数据,以提高网络的泛化学习能力,即120 000 个数据对。为了提高训练效率,采用了批训练方法,批大小为256,训练的学习率为0.000 1,训练优化算法为Adam 优化器[21],训练完成标志为训练集与测试集的损失函数均收敛至一个较小的稳定值。因此,将训练后的深度神经网络与已辨识的刚体动力学模型相结合,由此得到所提出的动力学模型。
为了验证所提出模型(DDM)的精度,将其与文献[20]中基于加权最小二乘法辨识的动力学模型(WLS)进行对比,其中各关节在力矩预测上的均方根误差(RMSE)如表1 所示,前三关节的计算力矩与实际力矩对比如图6所示。

表1 两种动力学模型在力矩预测上的均方根误差对比Table 1 Comparison of RMSE of two dynamic models in torque prediction
从表1看出,DDM模型在各个关节上均有更低的均方根误差,力矩误差下降幅度不少于20%,说明所提出的模型具有更高的精度;从图6看出,在关节速度反向的时候,DDM 的计算力矩曲线比WLS曲线过渡得更加圆滑且接近实际力矩曲线,这是因为WLS 曲线采用了库伦-粘性摩擦模型,其在速度反向时会产生力矩突变,从而造成较大的误差;而DDM 曲线采用深度神经网络,通过训练建立了网络输入与网络输出之间的映射关系,其不对具体的函数关系进行推导,从而具有更好的拟合能力。实验结果说明所提出的模型在保持高精度的同时,还能避免对摩擦力矩等因素进行复杂建模,降低模型的辨识难度。
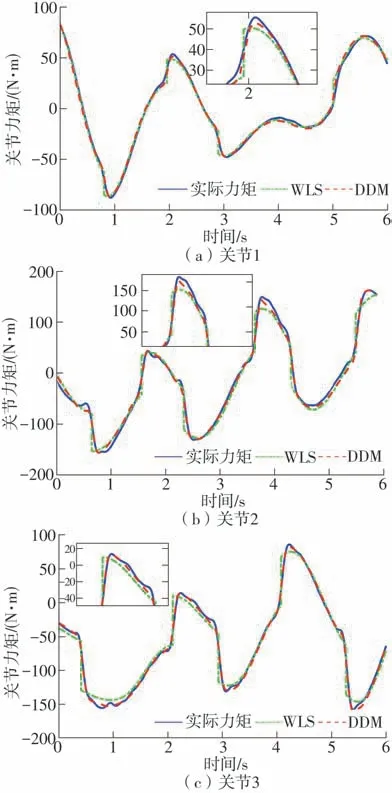
图6 两种动力学模型的计算力矩对比Fig.6 Comparison of calculated torques of two dynamic models
3.3 机器人拖动示教实验
为了使基于扰动卡尔曼滤波的外力矩观测器具有较优的性能,本文中通过实验反复调整,最终将卡尔曼滤波的协方差矩阵设置为对角矩阵且都为常数,如表2所示。具体调整方法可参考文献[5]。

表2 卡尔曼滤波中协方差矩阵参数Table 2 Parameters of covariance matrix in Kalman Filter
以第一关节与第五关节为例来分析所提出的拖动示教控制方案的有效性。其中系统惯性参数Mdi都设置为1,而系统阻尼参数标准值Dsti分别设置为10和5,其拖动实验效果如图7~8所示。从中看出,无论关节1 还是关节5,期望关节速度与关节外力矩的变化趋势非常接近,且期望关节转角产生了与外力矩相对应的运动角度,说明机器人关节能够顺应关节外力矩的作用而进行运动;同时,拖动过程中估计的外力矩在6 N·m之内,说明控制方案能实现轻松拖动机器人的效果。图7(c)与图8(c)可验证自适应阻尼方案的有效性。在正向运动的启动阶段,关节外力矩逐渐增大,系统阻尼参数随之逐渐减小以减小开始拖动时所需要的外力矩;在正向运动的拖动阶段,系统阻尼参数收敛至标准值附近以保持较好的拖动效果;在正向运动的刹车阶段,即关节准备反向运动或停止时,系统阻尼参数逐渐增大以使机器人关节快速停止;在正向运动停止后,关节反向运动的启动阶段时,由于式(25)中符号函数的作用,系统阻尼参数会快速下降至较低的值以使关节能够以较小的外力来进行反向运动;反向运动的拖动阶段与刹车阶段的系统阻尼参数变化特点与正向运动阶段类似。
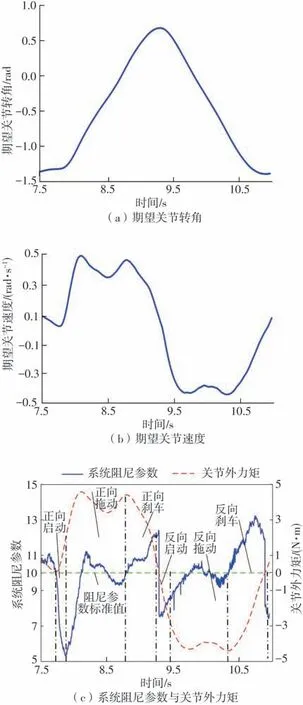
图7 关节1拖动实验Fig.7 Dragging experiment of joint 1
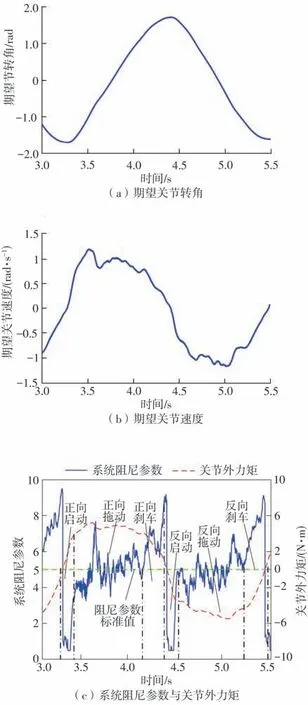
图8 关节5拖动实验Fig.8 Dragging experiment of joint 5
为了进一步分析自适应阻尼方法在示教启停阶段的作用,分别在有无自适应阻尼的方法下进行了两组对比实验,一是在关节外力矩相等的情况下,对比由外力矩所产生的期望关节速度的大小,如图9(a)所示;二是在期望关节速度相等的情况下,对比产生该期望关节速度所需要的关节外力矩的大小,如图9(b)所示。采用关节1拖动实验的数据进行分析,对比结果如图9所示。
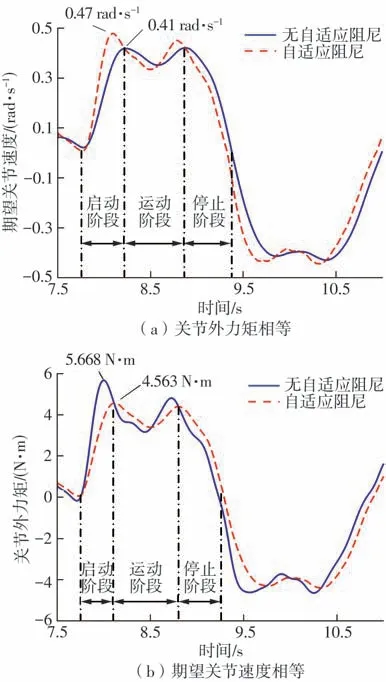
图9 自适应阻尼方法的对比实验Fig.9 Experimental comparison of adaptive damping methods
从图9(a)看出,在关节外力矩相等的情况下,相比于无自适应阻尼的方法,自适应阻尼方法在启动阶段所产生的期望关节速度更大,最大期望关节速度相差0.06 rad/s,说明自适应阻尼方法能够使机器人关节快速地启动;而在停止阶段,自适应阻尼方法产生的期望关节速度更小,其通过短暂地增大阻尼参数来减小由外力矩所引起的关节速度,使机器人关节能够快速地停止。从图9(b)看出,在期望关节速度相等的情况下,自适应阻尼方法下所需的关节外力矩更小,无自适应阻尼方法下的启动力矩最大值为5.668 N ⋅m,而自适应阻尼方法下为4.563 N ⋅m,下降幅度为19.49%,实验结果说明自适应阻尼方法只需要更小的外力矩就能启动机器人关节的运动,实现轻松的拖动示教。
综上所述,所提出的免力矩传感器拖动示教方法是有效的,机器人关节能顺应外力矩而进行运动,且自适应阻尼方法能有效地改善启动与停止阶段时的示教效果。
4 结论
(1)本文中提出了一种刚体动力学模型与深度神经网络相结合的机器人动力学模型,通过离线训练使深度神经网络学习并建立从关节转角、速度、加速度到刚体动力学模型的力矩残差的映射关系,当训练完成后,在刚体动力学模型的计算力矩上叠加深度神经网络输出的力矩项,由此完成动力学建模。实验表明,所提出的动力学模型相比于加权最小二乘法,在预测关节力矩上各关节均具有更小的均方根误差,且下降幅度不少于20%,提高了模型的精度的同时也避免了繁琐的摩擦力矩建模过程。
(2)本文中基于扰动理论建立机器人的关节外力矩模型,通过定义外力矩与广义动量为状态变量,将外力矩模型与动力学模型组合并转化为状态空间方程,从而基于卡尔曼滤波算法实现了机器人关节外力矩的免力矩传感器观测。
(3)本文中提出了自适应阻尼的导纳控制方法,将关节外力矩转换为对应的期望关节运动,其中系统阻尼参数随着外力矩的变化而自适应地进行调整,改善了启停阶段时的示教效果。实验表明,应用了自适应阻尼方法后,关节启动力矩可下降19%左右,更有利于机器人快速而轻松地开始与停止示教。

