基于改进动态规划法的HEV 多目标能量管理策略
赵克刚 何坤阳 黎杰 梁志豪 贝泾浩 王玉龙
(1.华南理工大学机械与汽车工程学院,广东广州 510640;2.广州华工机动车检测技术有限公司,广东广州 510640;3.广州汽车集团股份有限公司汽车工程研究院,广东广州 511434)
混合动力汽车的能量管理策略问题不仅关系到整车的燃油经济性,同时也与排放性,整车动力性等性能密切相关[1]。许多能量管理策略的研究侧重于提高燃油经济性,在优化过程中没有考虑其它目标,所获得的最优解牺牲了与之相冲突的其它目标[2]。为了提升混合动力汽车的综合性能,学者们在考虑燃油经济性的同时,也将电池损耗[3-5]、驾驶性能[6]、尾气排放[7-8]等指标纳入优化的范围,并提出了相关的多目标能量管理优化问题求解方法。
多目标进化算法是多目标能量管理策略优化问题常用的求解方法。Cheng 等[9]通过利用三种先进的多目标进化算法优化基于规则的混合动力汽车能量管理策略,验证了多目标进化算法运用于实际问题的可行性。秦大同等[4]基于多目标改进遗传算法对规则参数的优化结果,分析了规则参数对油耗和电池损耗的影响。耿文冉等[10]提出了基于粒子群优化算法和等效燃油消耗最小策略的多目标能量管理策略,实现了降低整车能耗并控制电池电量。文献[11]中以燃油消耗、SOC和排放性能作为能量管理策略优化目标,应用遗传算法实现了折中优化。然而,多目标进化算法依赖解的适应度值来引导对解空间的搜索,难以有效利用各阶段决策变量之间的关联性信息提高搜索效率[12];同时,多目标进化算法本身的收敛性并不总是能够保证的,求解结果未必是最优的[13]。
DP算法作为一种收敛性能保证的确定性算法,常用于求解能量管理策略等多阶段决策问题[13]。加权法可以将多目标优化等效转化为单目标优化进行求解[14],因此,学者们通常将加权法和动态规划法结合起来处理多目标能量管理策略。文献[15-17]在研究以提高燃油经济性和保护电池为目标的能量管理策略时,基于加权法建立了性能函数,应用动态规划法求解了该优化问题,并分析了不同权系数对求解结果的影响。隗寒冰等[18]将燃油消耗量和HC、NOx、CO的排放量的优化目标归一化处理,并用加权法将各目标处理为单目标函数,最终利用DP算法完成求解。由文献[19]可知,通过加权法转化所得的单目标优化问题的最优解必是原多目标优化问题的非支配解。多目标优化的意义在于求取非支配解集以供设计者根据设计需要选择[6]。然而,应用加权法选取一个权重系数只能获得一个最优解,因此需要遍历一定范围内的权重系数才能获得问题的非支配解集。遍历权重系数的主要问题在于权重系数的均匀分布不一定产生一个均匀分布的非支配解集,且反复求解单一优化问题将造成相当大的计算负担。
针对现有的多目标能量管理策略求解算法存在的不足,在保证充分发挥动态规划法的收敛性和全局优化特性的前提下,本文将动态规划法拓展到多目标优化领域,提出了非支配排序动态规划法。
1 非支配排序动态规划法
根据动态规划法的求解思想,将多目标多阶段决策问题依据时间或空间划分为N个子阶段问题,每个子阶段问题都有现阶段的容许状态变量空间以及对应的容许控制变量空间。多目标多阶段决策问题的数学模型可表示为
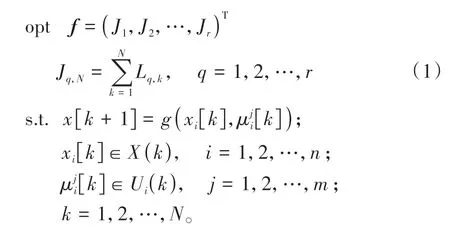
式中:f为目标函数向量;Jq,k为第k个子阶段的第q个目标函数累积值;X(k)为第k阶段容量为n的容许状态空间,用xi[k]表示X(k)中的第i个状态变量;Ui(k)为在第k阶段第i个状态下容量为m的容许控制集合,用表示X(k)中的第j个状态变量;为状态转移方程,x[k+1]为k阶段作出的决策通过状态转移方程求得第k+1阶段所处的状态。
在每个阶段通过决策,即可求得现阶段瞬时代价函数
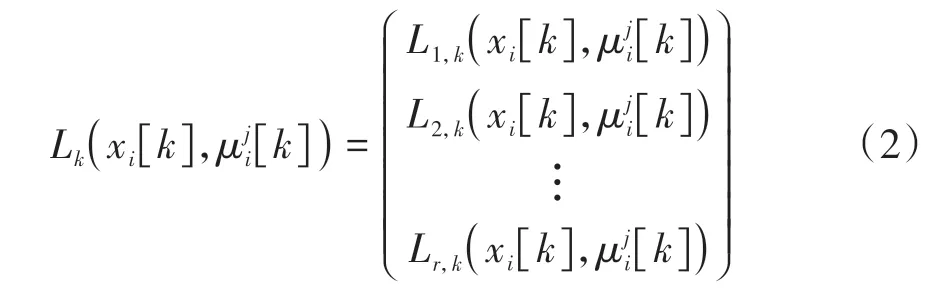
对于每个阶段中某个状态变量,首先求取它在不同允许控制变量下产生的瞬时代价函数值,然后通过状态转移方程得到下一阶段所处状态以及对应的累积目标函数值,相加求得现阶段的累积目标函数值,即:

实际上,遍历整个允许状态空间求得的是所有状态在不同控制策略下的累积目标函数值集合Jk(X(k))。为获得整个问题的最优控制策略,要保证每个阶段中确定的策略是最优的。因此,需在Jk(X(k))内进行寻优以获取最优解optJk(xi(k))及对应的控制策略。然而,对于多目标问题,每个阶段求得的累积目标函数值为向量,应用传统的动态规划法难以完成寻优过程。
在多目标问题中,难以同时使所有优化目标达到最优,一般只能获取一组各目标折中权衡的非支配解集作为最优解。在每个阶段的寻优过程中应用快速非支配排序算法[20],对求得目标函数累积向量集进行非支配排序可获得现阶段的非支配解集,即:
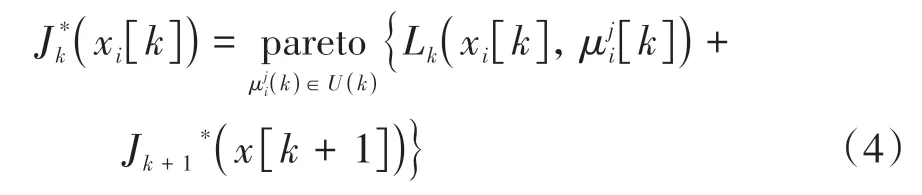
依序逆向递推至初始阶段,便可得到关于整个问题的非支配解集以及对应的最优策略,即整个问题的解。
2 多目标能量管理优化问题的构建
本节以混联式混合动力汽车为研究对象,将最小化燃油消耗量和电池损耗作为优化目标,构建多目标能量管理策略优化问题。
2.1 目标函数
根据一种基于损耗累积模型的混合动力汽车电池寿命估计方法[21],可通过计算电池有效安时流通量来评估电池的实际消耗。因此,对于考虑燃油消耗和电池损耗的能量管理策略问题,目标函数为

式中:Be为发动机的燃油消耗量;Aheff为有效安时流通量;be为瞬时燃油消耗量;I为流经动力电池的电流;σ表示电池在不同工作条件下电荷转移的强度,称为强度系数。为了计算方便,本文用安培(A)与时间秒(s)的乘积表示有效安时流通量,其单位表示为A·s。
发动机的瞬时燃油消耗量可简化为发动机转速和转矩静态函数[22],即
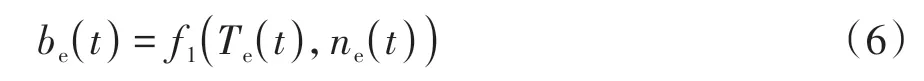
式中,Te,ne分别为发动机的工作转矩和转速。
2.2 动力学约束条件
在能量管理策略的研究中主要关注车辆的经济性表现,因此只考虑车辆的纵向速度变化而忽略其他影响。根据车辆纵向动力学模型[23],驱动轮端的需求转矩受行驶工况的道路滚动阻力系数f和坡度角α以及行驶车速u和加速度a影响,驱动轮端需求功率P可用数学公式表示为
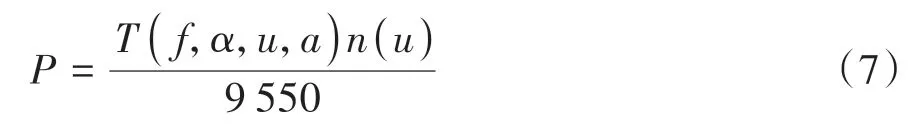
式中,T为驱动轮端的需求转矩,n为驱动轮端的需求转速。
不同构型的混合动力汽车,其动力源部件布置与耦合方式不尽相同,但从本质上说,整车稳定行驶所需要的功率均来自发动机和电池输出的功率:

式中,P为需求功率,Pe为发动机输出功率,Pb为动力电池输出功率;ηt为传动系机械效率。
两个电机的输出功率分别为Pm1、Pm2,它们的工作效率主要与工作时的输出转矩和转速有关,可表示为

式中:Tm1、Tm2和nm1、nm2分别为两个电机的转矩和转速;ηm1、ηm2分别为两个电机的工作效率。
各动力部件的输出功率可通过式(10)计算,

式中:Ti、ni分别为动力部件输出的转矩和转速。
混合动力汽车的各动力部件的转速转矩与整车需求转速转矩通过特定的方式耦合起来,耦合方式分为转矩耦合、转速耦合和功率耦合速[24],可分别用方程式(11)、(12)、(13)表示:
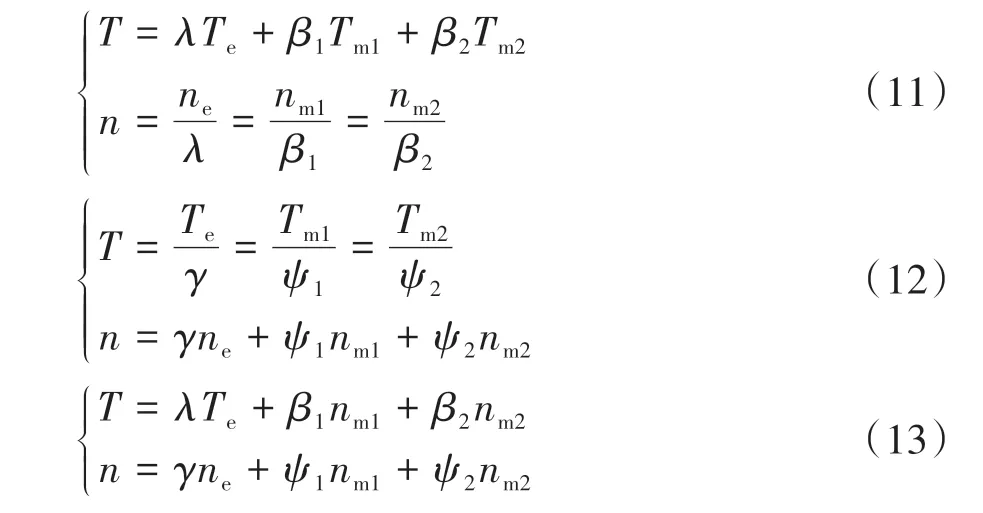
式中:λ、β1、β2、γ、ψ1、ψ2均为耦合机构的特性系数。
为保证混合动力系统的正常使用,动力部件的转速ni应在转速范围[ni_min,ni_max]内,输出转矩Ti应在相应的允许范围[Ti_min(ni),Ti_max(ni)]内,i=e,ml,m2 分别代表发动机、电机1、电机2;电池荷电状态SOC 和输出功率Pb分别不能超出[SOCmin,SOCmax]和[Pb_min,Pb_max]。
2.3 求解步骤
应用NSDP 求解多目标能量管理优化问题的具体步骤如下。
步骤1将功率分配比(电池输出功率与整车需求功率之比)作为控制变量μ,将电池SOC 作为状态变量x。
步骤2设定非支配解集中解的最大个数pareto-num,将问题划分为N个阶段,各阶段有m个状态变量,每个状态变量对应有n个控制变量;令k=N。

步骤7对于第k阶段的每个xi[k],重复步骤3-步骤6,即可获得该阶段整个非支配解集;k=k-1。
步骤8重复步骤3-步骤7,直至k=1,便可获得整个问题的非支配解集。
3 仿真与分析
为验证NSDP的有效性,本节设计了如下实验。
1)算法性能对比实验 分为4个小实验,实验1和实验2 分别以功率分流式HEV 和串并联式HEV作为仿真对象,在NSDP 中设置不同的非支配解集个数,分析解集个数对求解结果的影响;实验3和实验4在前两个实验的基础上应用WDP 和NSDP 求解在匀加速工况的多目标能量管理策略,对比两种算法的求解性能;
2)WLTC工况仿真实验 利用NSDP求解第二款方案的混合动力汽车在WLTC工况的多目标能量管理优化问题,获得非支配解集并进行分析。
3.1 动力系统概况
3.1.1 方案一
方案一为功率分流式混合动力系统,由发动机、两个电机、动力电池以及行星齿轮机构等组成,其结构形式如图1所示。整车质量m=1 710 kg,车轮半径r=0.317 m,动力系统参数如表1所示。
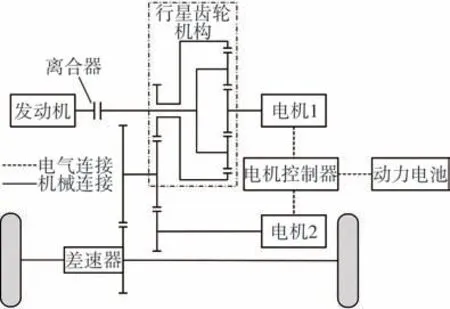
图1 混合动力系统构型图(方案一)Fig.1 Hybrid power system configuration diagram(Option 1)

表1 动力系统参数(方案一)Table 1 Power system parameters(Option 1)
该混合动力系统各动力部件的转速转矩与整车需求转速转矩耦合方程为

式中,u为目标车速,im2为电机2到轮端的传动比,iPG为行星齿轮机构的齿圈到轮端的传动比,r为车轮半径。
动力电池输出功率的计算公式为
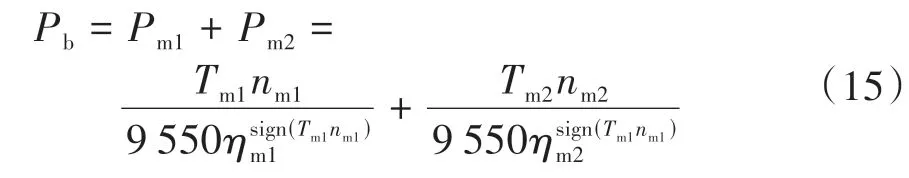
式中,sign(z)表示求取z的符号的函数。
3.1.2 方案二
方案二为串并联式混合动力系统,主要包括发动机、驱动电机、离合器、ISG电机和动力电池等零部件,发动机可与ISG 电机构成辅助动力单元(APU),组成结构如图2所示;整车质量m=1 710 kg,车轮半径r=0.317 m,其动力系统参数如表2所示。
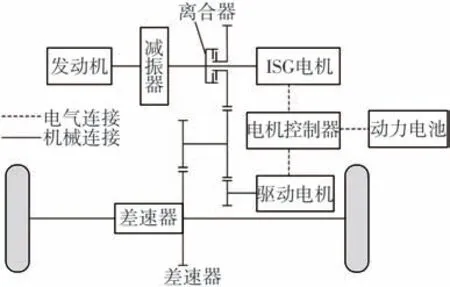
图2 混合动力系统构型图(方案二)Fig.2 Hybrid power system configuration diagram(Option 2)
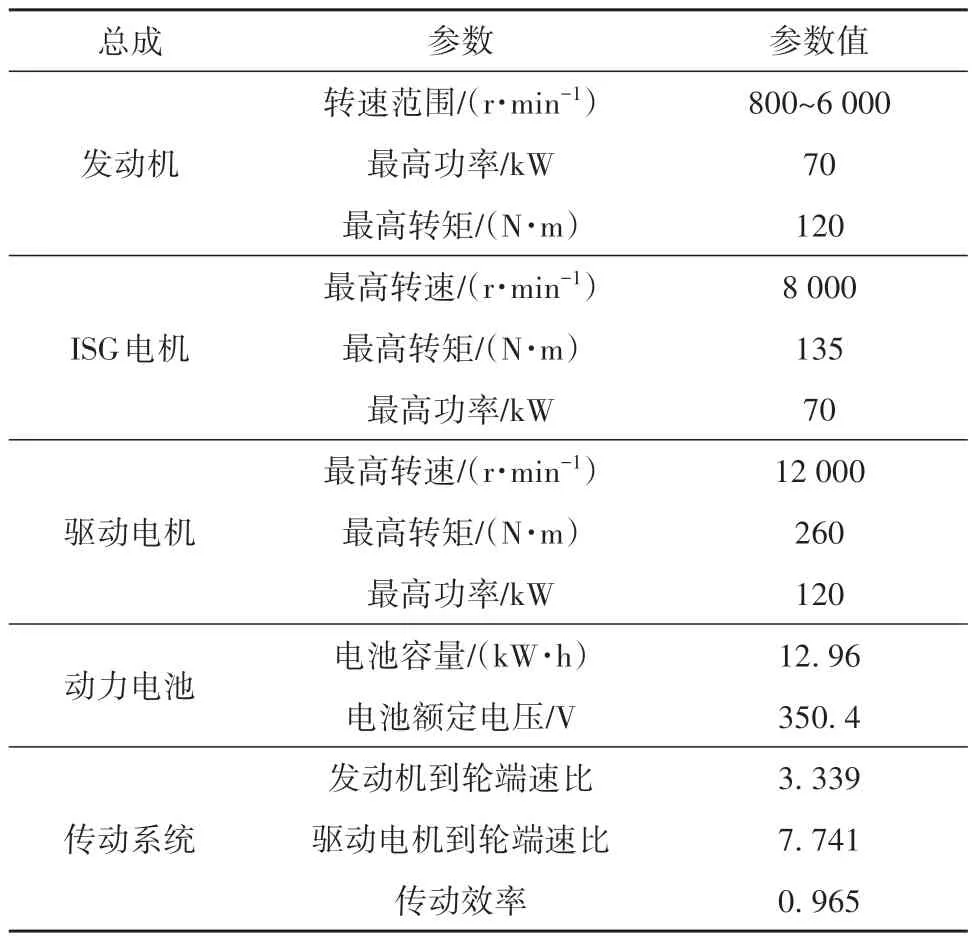
表2 动力系统参数(方案二)Table 2 Power system parameters(Option 2)
该混合动力系统的动力学方程可表示为
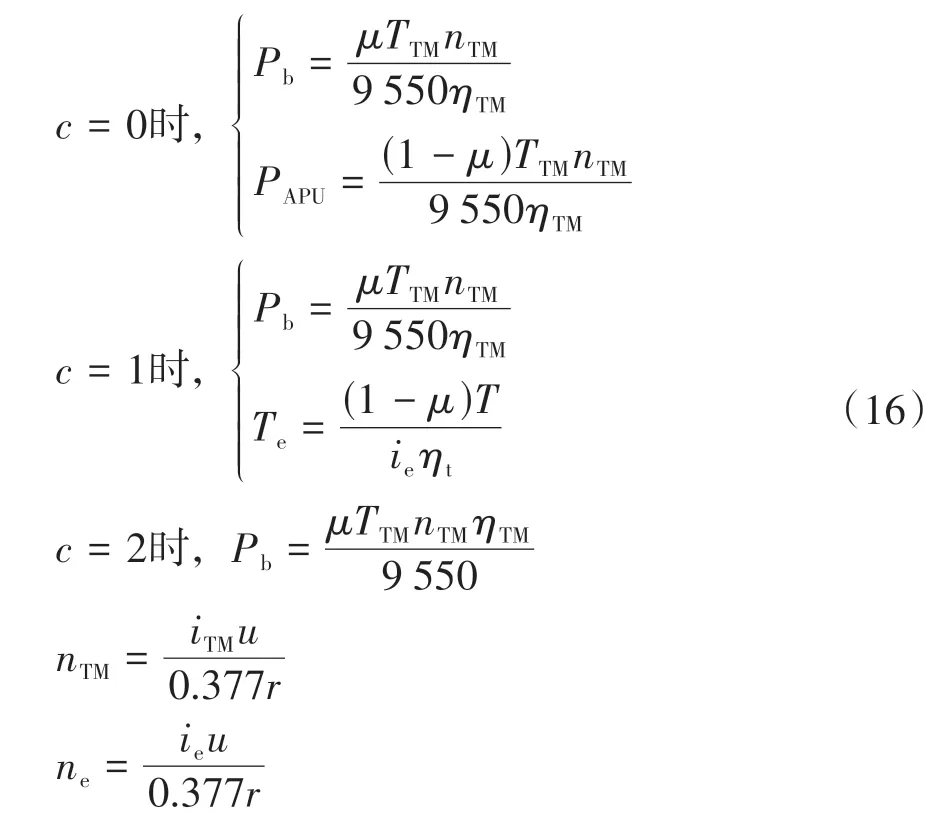
式中:PAPU为APU 的输出功率;ηTM为驱动电机的工作效率;TTM、nTM分别为驱动电机的输出转矩和输出转速;μ为功率分配比;ie和iTM分别为发动机和驱动电机到驱动轮端的速比;当c=0 时,表示离合器处于分离状态,混合动力系统处于纯电驱动或串联驱动模式,其中串联驱动模式包括APU直驱模式(整车需求功率完全由APU提供)、串联放电模式(整车需求功率由APU和电池共同提供)和串联充电模式(APU 的输出功率一部分供给驱动电机、一部分供给电池充电);当c=1 时,表示离合器处于接合状态,混合动力系统处于并联或发动机直驱模式;当c=2 时,表示混合动力系统以制动能量回收模式进行工作。
3.2 算法性能对比实验
本次实验的比较对象为NSDP和WDP,而后者在处理时间较长的复杂仿真工况时将面临“维数灾难”,倘若利用WDP 进行遍历多个权重系数的仿真,计算机的存储硬件将面临很大的挑战,且时间成本也将会是巨大的。因此,本次实验选取一段简单的匀加速工况(0~96.6 km/h)作为仿真工况,既能体现不同车速下基于两种算法的能量管理策略对HEV的控制效果,又能兼顾现实的软硬件条件。此外,每个小实验中两个算法的程序均维持在工况前后电池SOC不变。
3.2.1 实验1和实验2
为了分析最大非支配解个数对NSDP 求解结果的影响,实验1和实验2分别以功率分流式HEV 和串并联式HEV为仿真对象,将NSDP的最大非支配解个数设置为40、80、120、160和200来求解上述匀加速仿真工况下的多目标能量管理策略,求解结果如图3和表3所示。
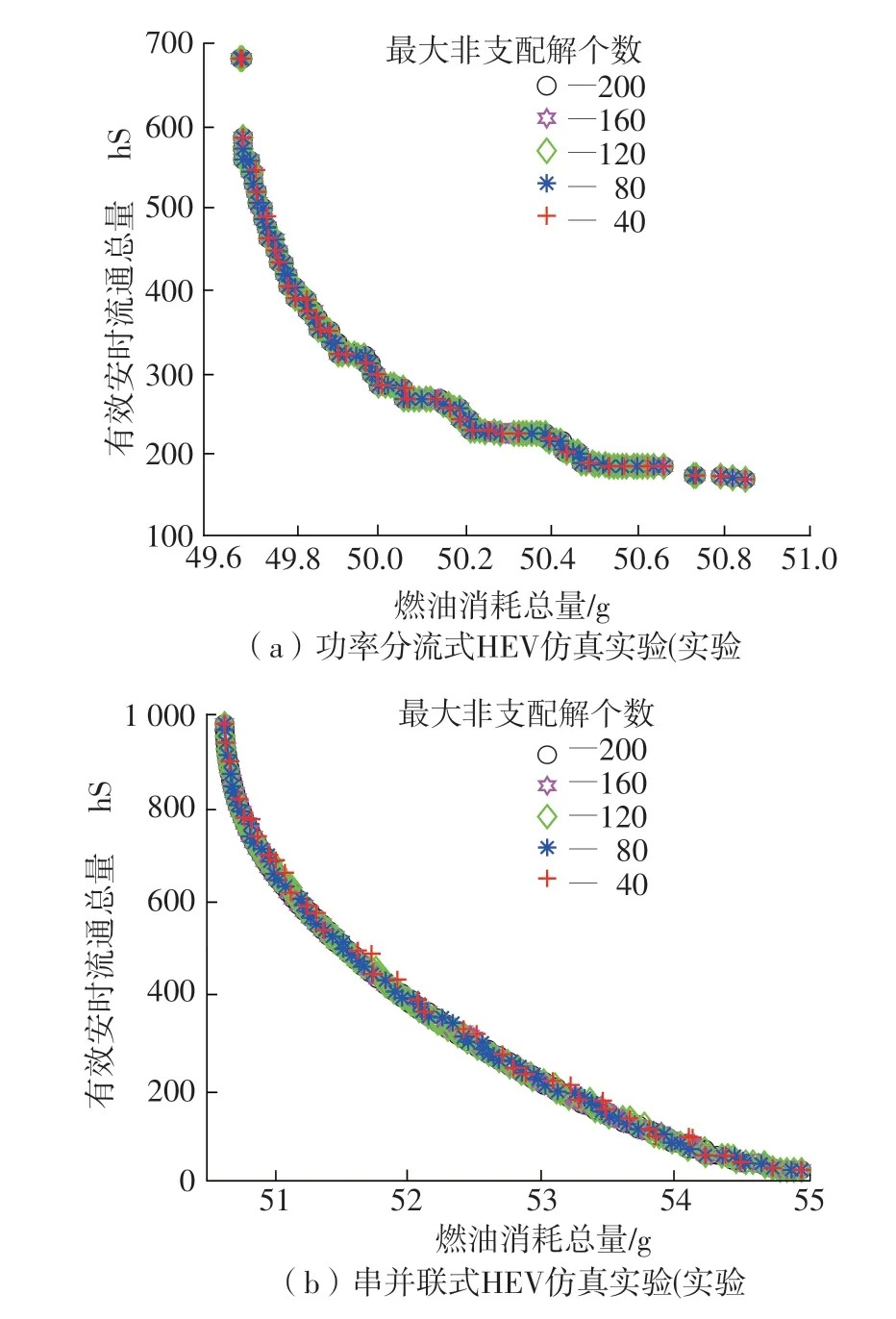
图3 实验1和实验2的求解结果Fig.3 Solution results of experiment 1 and experiment 2
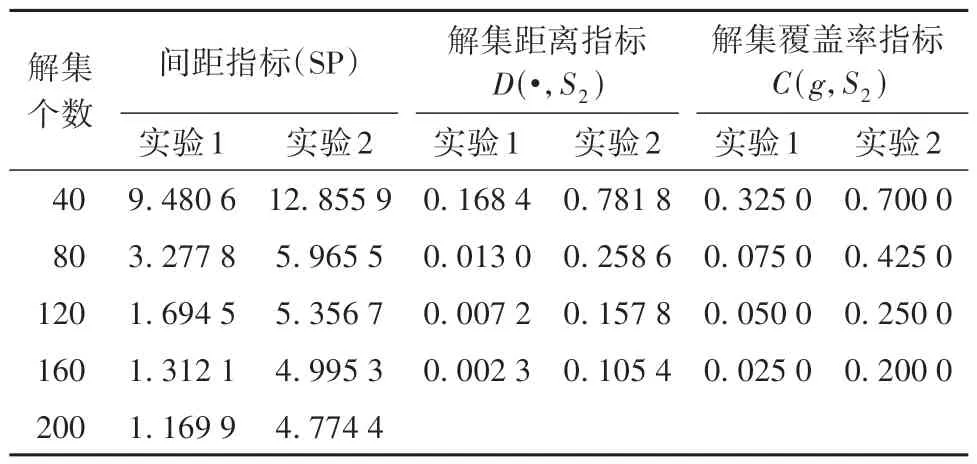
表3 实验1和实验2求解结果中的指标值[26-29]Table 3 Index values in the solution results of experiment 1 and experiment 2
表3 中,解集距离指标D(S1,S2)用来度量两个解集之间的最小平均距离,S1和S2是同一个多目标优化问题的两个解集,用|S|表示解集S中解的个数,用vi表示解集S1中第i个解,d(vi,S2)表示vi和S2中的点的最小欧式距离,则它们之间的距离可以根据式(17)计算。
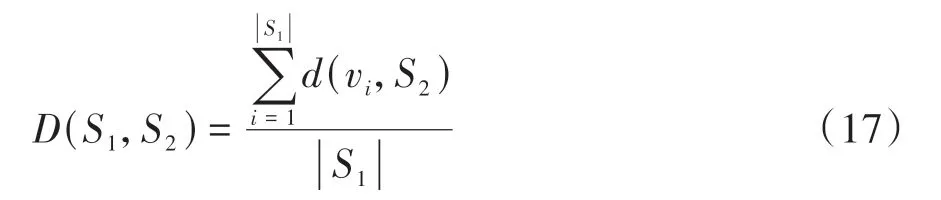
解集覆盖率指标C(S1,S2)计算的是解集S1中被解集S2中至少一个解支配的解的数目占解集S1所有解的个数的比例,它的数学描述为
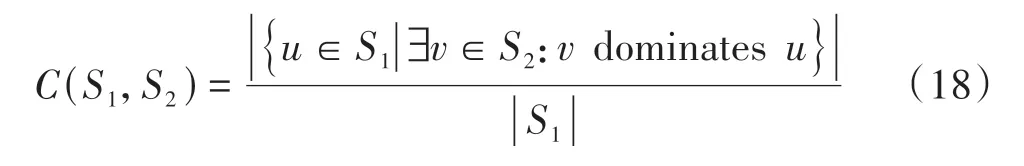
本小节计算的各个解集距离指标D(•,S2)和解集覆盖率指标C(g,S2)中的g为各解集,S2均为最大非支配解个数为200的解集。
由图3 看出,尽管设置的最大解集个数不同,但两个实验的各解集均在对应的同一个pareto 前沿附近。同时根据表3,以数量设置为200 的解集作为参考,其它解集的距离指标和覆盖率指标的值并不大。因此,在40~200 范围内,最大解集个数对算法的求解结果收敛性影响较小。对于SP 指标,它可以度量解集在目标空间的分布均匀性,从两个实验可以看出,随着最大解集个数的增大,解集的均匀性有所提升;然而,从实验结果来看,解集个数从120 到200 的均匀性提升却不大。所以,可以选择将NSDP的最大非支配解集个数设置为120。
3.2.2 实验3和实验4
为了对比NSDP 和WDP 的算法性能,将NSDP的非支配解集最大解个数设置为120,WDP算法的权重系数ω也在[0,1]范围内均匀取120 个值,二者在同一个计算平台进行仿真实验3 和实验4,仿真工况为匀加速工况,仿真对象分别为功率分流式HEV 和串并联式HEV。将两个实验的两组解集绘制到同一坐标系下,如图4所示。计算两种算法的各个性能评价指标值,结果如表4所示。

图4 实验3和实验4求解结果Fig.4 Solution results of experiment 3 and experiment 4

表4 实验3和实验4求解结果中的指标值[26-29]Table 4 Index value in the solution results of experiment 3 and experiment 4
由表4可知,尽管WDP在[0,1]范围内均匀取了120个权重系数值,但是两个实验最终分别只获得了14、46 个有效解。这是因为对于离散问题,权重系数的微小改变不足以改变决策,从而使得相差较小的权重系数最终所获得的结果相同。
HV 指标能够同时评价所求解集的收敛性和广泛性,在两个实验中,求解结果的HV 指标相差分别为1.606 8%和0.805 6%,两种算法的收敛性和广泛性表现相近。根据解集距离指标计算结果以及由图4 所示,NSDP 算法的解集很接近WDP 算法的解集;实验3 中C(NSDP,WDP)和C(WDP,NSDP)分别为0.050 0和0.066 7,说明两个算法仅有个别解支配另一算法的解;实验4 中C(NSDP,WDP)和C(WDP,NSDP)均为0,说明两种算法的解集互不存在支配关系。综上所述,NSDP 能够保证动态规划法的收敛性和广泛性。
在实验3中,WDP的SP指标(40.038 4)远大于NSDP 的SP 指标(1.713 0),表明NSDP 所获得解集的均匀性明显优于WDP 所获解集的均匀性。在实验4中,两种算法求解结果的SP指标相差不大,说明它们所获得解集的均匀性表现接近。可见,利用WDP 均匀遍历权重系数并不能保证获得均匀的解集。在实验4 中,WDP 和NSDP 所求得的解集非常的相近,个别解存在一定的差别,主要原因是在NSDP 求解过程中每个阶段都会根据拥挤度舍弃掉一部分的非支配解。
在同一计算平台下求解匀加速工况下的多目标能量管理策略问题,两次实验NSDP 求解花费时间分别为621 s和2 518.8 s,而WDP 求解花费的时间分别为66 046 s 和297 354.1 s,分别是NSDP 的106 倍和118 倍。这说明NSDP 在求解效率方面具有显著的优势。
3.3 WLTC工况仿真实验
本小节面向方案2 构型HEV,根据GB19578—2021《乘用车燃料消耗量限值》,选取WLTC 工况作为仿真工况,并利用NSDP 求解。根据3.2 节的结论,在区间[40,200]内,最大非支配解个数并不会显著影响算法的收敛性和均匀性,且考虑到WLTC 工况时间更长以及兼顾算法的求解效率,将NSDP最大非支配解个数也设置为120。计算平台为64 位Win10 操作系统,配置8 核i7-8700K 3.70GHz的CPU,64GB物理内存。
NSDP 最终获得有效解个数为120 个,求解时间为54 882 s,非支配解集如图5 所示。若采取加权的动态规划法,由3.2 节实验可估计所需的时间约为1 525 个小时,且难以获得均匀的、能反映仿真对象特性的求解结果,这显然不能令人满意。
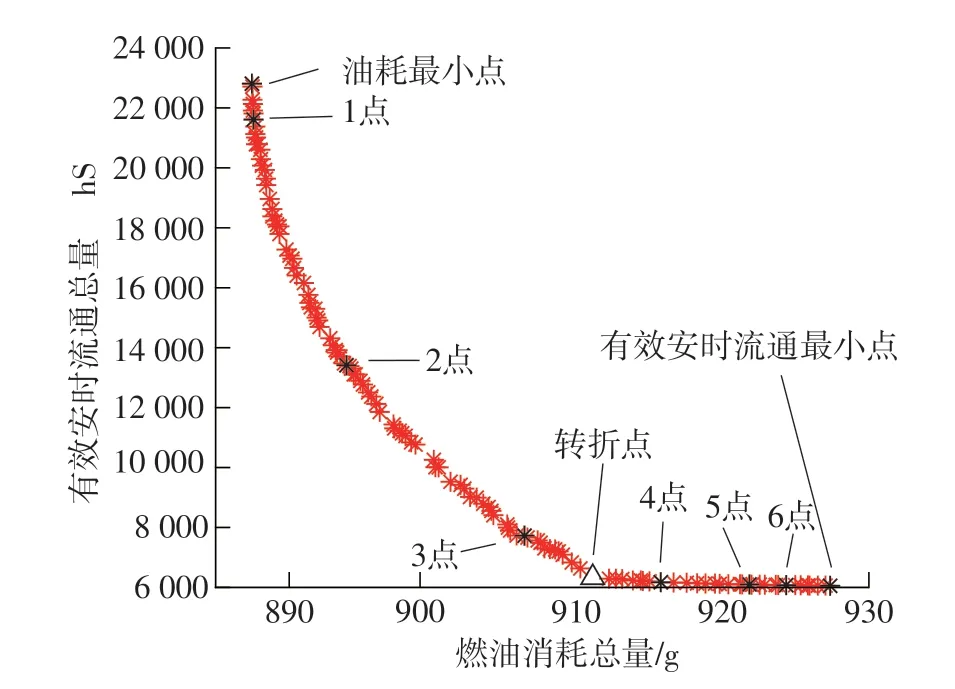
图5 WLTC工况下的非支配前沿Fig.5 Non-dominated frontier under WLTC
由图5可知,随着燃油消耗总量的增加,有效安时流通总量在不断减少,但是其减少的速率也在不断降低。在到达某一个点(转折点)后,燃油消耗总量的增加并不会造成有效安时流通总量的明显减少。为了探究出现这一现象的原因,选取转折点前后各3个点的求解结果进行分析,具体求解结果如表5所示。
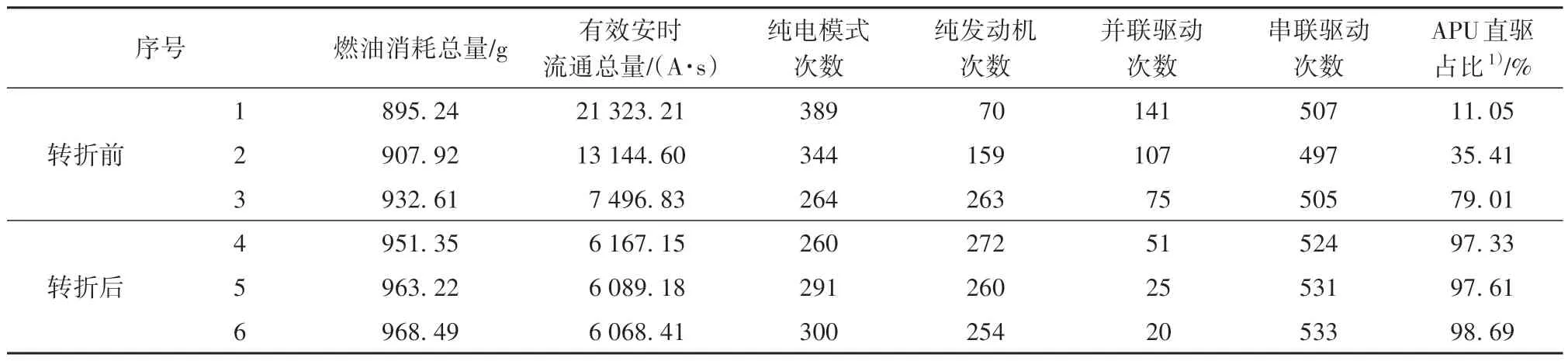
表5 转折点前后各3个点的求解结果Table 5 Solution results of 3 points before and after the turning point
为了更清晰展现不同非支配解之间的差异,图6是表5中各点的SOC变化曲线和工作分布点。由表5和图6可以得出,在转折点前,燃油消耗量的增加主要是因为采用纯发动机驱动模式次数的增加,而有效安时流通总量减少的主要原因则是采用纯电驱动模式的次数减少。从油耗最小点变化到有效安时流通总量最小点,在车速较高和需求转矩较大的工况下使用并联驱动模式的次数越来越少,取而代之的是串联驱动(包含APU 直驱);相对于转折点前,转折点后采用APU直驱模式占比的增加,这是燃油消耗量增加而不会引起电池有效安时流通总量的剧烈变化的主要原因。因为在此工作模式下,APU消耗燃油产生的电流不经过动力电池而全部供给驱动电机。

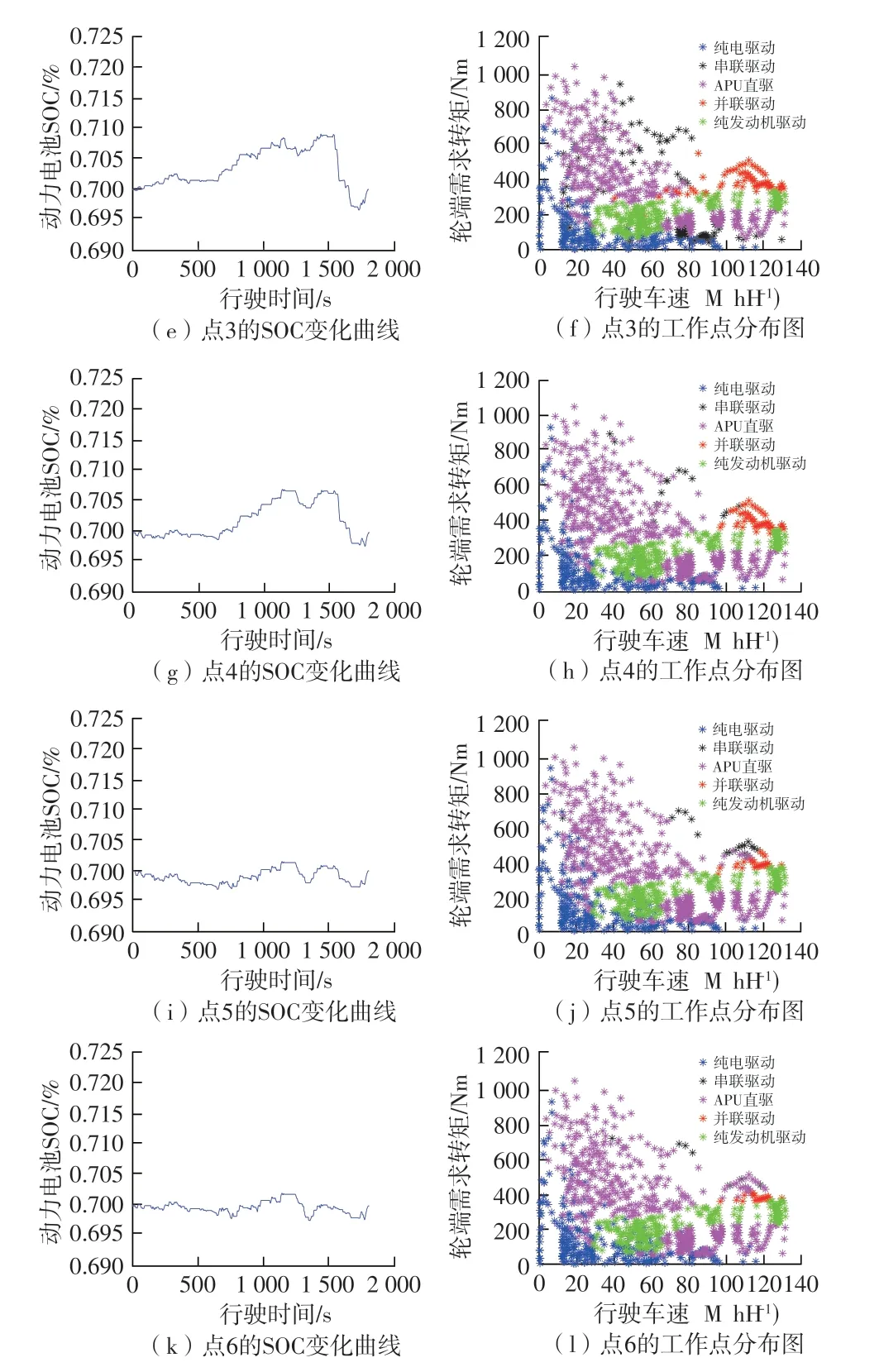
图6 SOC变化曲线和工作分布点图Fig.6 SOC change curve and work point diagram
非支配解集转折点求解结果相对于油耗最小点燃油消耗总量增加了5.26%,而有效安时流通总量降低了72.29%,大幅降低了动力电池的寿命损失;从转折点到有效安时流通总量最小点变化不大,而燃油消耗总量变化明显,电池寿命损耗的降低将牺牲较大的燃油经济性。因此,可以选择转折点优化的最终结果。对于NSDP 的求解结果,工程人员也可以根据设计的需求选取其他解作为最终优化结果。
4 结论
为了高效高质量地求解混合动力汽车多目标能量管理优化问题,本文将动态规划法和非支配排序法两者的求解思想有机结合,设计了NSDP 算法。通过算法性能对比实验看出,NSDP 不仅能够保持动态规划法的收敛性和广泛性,而且能稳定地获得均匀的非支配解集。同时,NSDP 所需的求解时间仅不到WDP的1%,在求解效率方面有显著优势。
应用NSDP 完成了某款串并联式混合动力汽车在WLTC仿真工况下的多目标能量管理优化问题的求解,并针对求解结果进行了分析。借助于NSDP这一求解工具,可高效地获得多目标能量管理策略优化问题非支配解集,相关技术人员可通过非支配解集充分了解最优策略下各个指标之间的相互关系,总结其中规律,为实际能量管理策略的设计做准备。

