基于GNN双源学习的访问控制关系预测方法

单棣斌，杜学绘，王文娟，刘敖迪，王娜

基于GNN双源学习的访问控制关系预测方法

单棣斌，杜学绘，王文娟，刘敖迪，王娜

（信息工程大学，河南 郑州 450001）

随着大数据技术的迅速发展和广泛应用，用户越权访问成为制约大数据资源安全共享、受控访问的主要问题之一。基于关系的访问控制（ReBAC，relation-based access control）模型利用实体之间关系制定访问控制规则，增强了策略的逻辑表达能力，实现了动态访问控制，但仍然面临着实体关系数据缺失、规则的关系路径复杂等问题。为克服这些问题，提出了一种基于GNN双源学习的边预测模型——LPMDLG，将大数据实体关系预测问题转化为有向多重图的边预测问题。提出了基于有向包围子图的拓扑结构学习方法和有向双半径节点标记算法，通过有向包围子图提取、子图节点标记计算和拓扑结构特征学习3个环节，从实体关系图中学习节点与子图的拓扑结构特征；提出了基于有向邻居子图的节点嵌入特征学习方法，融入了注意力系数、关系类型等要素，通过有向邻居子图提取、节点嵌入特征学习等环节，学习其节点嵌入特征；设计了双源融合的评分网络，将拓扑结构与节点嵌入联合计算边的得分，从而获得实体关系图的边预测结果。边预测实验结果表明，相较于R-GCN、SEAL、GraIL、TACT等基线模型，所提模型在AUC-PR、MRR和Hits@等评价指标下均获得更优的预测结果；消融实验结果说明所提模型的双源学习模式优于单一模式的边预测效果；规则匹配实验结果验证了所提模型实现了对部分实体的自动授权和对规则的关系路径的压缩。所提模型有效提升了边预测的效果，能够满足大数据访问控制关系预测需求。

大数据；基于关系的访问控制；边预测；图神经网络

0 引言

大数据的广泛应用，有力推动了社会进步与经济发展。但是大数据在迅速发展的同时，面临诸多安全威胁，其中用户越权访问资源是制约大数据资源安全共享、受控访问的主要问题。

访问控制是实现大数据安全可控的重要技术手段之一。由于大数据具有资源数量巨大、资源动态生成、主体客体关系复杂等特点，传统的访问控制模型，如自主访问控制（DAC，discretionary access control）、强制访问控制（MAC，mandatory access control）、基于角色的访问控制（RBAC，role-based access control）等，处理大数据访问控制时，会面临访问控制策略配置负担重、静态策略不能预判动态资源生成、难以满足复杂数据用户关系与类型的安全约束等问题[1]。

基于关系的访问控制（ReBAC，relationship- based access control）[2-4]将实体之间（如主体与主体、主体与客体等）的关系路径RP（relationship path）[5-6]作为已知的基础数据，并利用这些数据制定基于关系的访问控制规则。ReBAC实现了对基于属性的访问控制[7]策略的扩展[3,6]，增强了访问控制策略的逻辑表达能力，使访问控制变得更加动态和灵活。文献[8-12]研究了ReBAC策略挖掘和学习算法，实现了将传统访问控制规则转化为ReBAC规则，便于ReBAC策略的应用与发展。但是在社交网络、购物平台、电子医疗等大数据平台中，人工、半人工建立的关系数据通常是有限的、不完整的，而关系数据的缺失不可避免地会影响基于关系访问控制规则的完备性，并且会增加访问控制规则中关系路径的复杂度。

针对实体关系数据缺失问题，可以通过预测和补全隐含存在的实体之间的关系及类型来解决。由于大数据系统中的实体关系数据集可构成以实体为节点、实体关系为边的大规模、复杂的有向多重图，因此关系预测和补全本质上是关系图中节点之间的边预测问题。

传统的边预测方法[13]，主要通过计算目标节点相似性得分、分解网络的矩阵表示等实现边预测。随着图神经网络（GNN，graph neural network）技术的发展与应用，基于图神经网络的边预测方法，如R-GCN（relational graph convolutional network）[14]、SEAL（learning from subgraphs，embeddings and attributes for link prediction）[15]、GraIL（graph inductive learning）[16]、TACT（topology-aware correlations）[17]等模型，通过图形拓扑、节点与边特征的学习实现对目标节点进行边预测，实验结果显示其预测结果优于传统方法[18-21]。

但是基于图神经网络的边预测方法在处理复杂关系图时，存在以下问题。一是R-GCN、SEAL、GraIL、TACT等边预测模型的学习信息不够全面，没有同时兼顾拓扑结构特征、节点自身特征、节点类型等要素信息，降低了图表示能力。二是SEAL、TACT等模型在拓扑结构学习过程没有考虑边方向、边类型、多重边等特征，会将非同类别的边或节点归为一类，不同类型的边预测时可能造成混淆。三是R-GCN、SEAL等模型没有区分和学习不同邻居节点的不同权重，可能造成节点嵌入特征受到非关键邻居节点的干扰。以上3个方面降低了边预测结果的准确性。

为克服现有边预测技术在解决复杂关系图网络边预测问题时的不足，本文提出了一种基于图神经网络双源学习的边预测模型。该模型依据关系数据集建立实体关系图，将大数据访问控制实体关系预测问题转化为有向多重图的边预测问题；提出了基于有向包围子图的拓扑结构学习方法，通过有向包围子图提取、子图节点标记计算和拓扑结构特征学习3个环节，从实体关系图中学习其节点与子图的拓扑结构特征；提出了基于有向邻居子图的节点嵌入学习方法，通过有向邻居子图提取、节点嵌入特征学习等环节，学习其节点嵌入特征；设计了双源融合的评分网络，将拓扑结构特征与节点嵌入特征联合计算目标节点间边的得分，从而得到边预测结果。

1 相关研究

1.1 边预测优化ReBAC的可行性分析

边预测，也被称为链接预测，是预测网络中两个节点之间是否存在边（链接）的问题[22]。由于图网络的普遍存在，边预测在许多领域得到了应用[13]，如社交网络中的朋友推荐[23]、论文引用网络中的合著作者预测[24]、药物反应预测[25]、知识图的补全[26]等。边预测研究[13]主要包括传统边预测方法和基于GNN的边预测方法。

ReBAC规则是基于实体关系路径[27-29]制定的，与访问控制相关的实体（作为节点）和它们之间的关系（作为边）构成了实体关系图。通过对实体关系图进行边预测，可以学习到潜在的实体关系，解决其面临的关系缺失问题，从而增强ReBAC自动化动态授权的能力，简化基于原有关系建立的访问控制规则。

以某医疗信息系统的ReBAC策略为例，系统中包括基于关系的访问控制规则[8]（为明确问题，本文对该规则进行了适度简化）如下。规则1：医生可以查阅他/她所属的医疗团队治疗的患者的电子健康记录（HRs，health records），表示为 team patientresource，{read}>。规则2：管理电子健康记录的医生可以查阅这些电子健康记录，表示为resource, {read}>。

原始的实体关系图（如图1(a)所示）中，节点、、表示医生doctor，节点表示医疗团队team，节点表示患者patient，节点表示电子健康记录HR。其中，医生属于团队，医生是的团队同事，医生负责管理电子健康记录。关系1表示团队同事teammate_of，2表示属于成员part_of，3表示治疗关系treat，4表示拥有have，5表示管理manage。健康记录的拥有者是患者，由团队进行治疗，即节点与节点之间组成一条关系路径1：<2><3><4>，满足规则1，所以可以查阅。医生管理电子健康记录HRs，即节点与节点之间组成一条关系路径2：<5>，满足规则2，所以可以查阅。

通过边预测，可以对实体实现自动化的动态授权。例如，图1(b)中，节点与节点满足关系：<1>，即医生是的团队同事。节点满足<2>，如果可以预测<2>，则与也满足关系路径1，即满足规则1，医生也可以查阅健康记录，那么自动为医生进行授权。

通过边预测，可以简化匹配ReBAC规则中的关系路径。例如，图1(b)中，节点与节点满足关系：<1>，即医生是的团队同事。节点满足<5>，如果可以预测<5>，则满足规则2，医生可以查阅，那么将原来匹配的关系路径<2><3><4>简化为关系路径<5>。

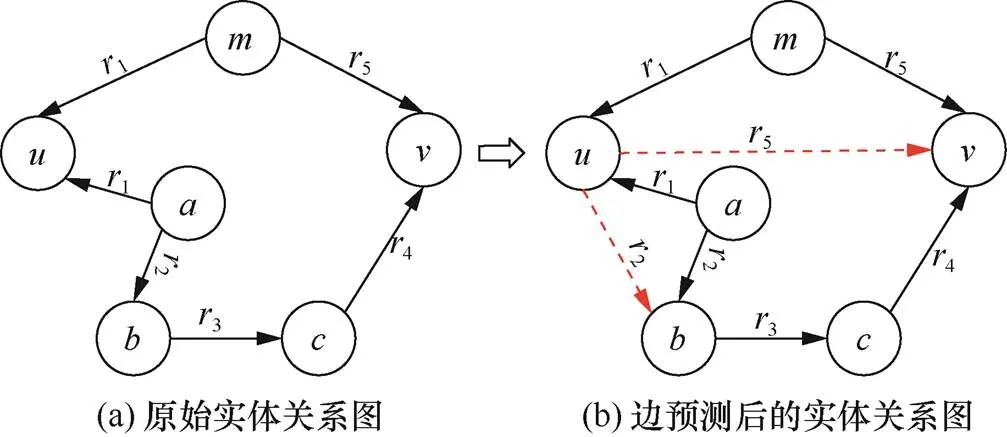
图1 边预测优化ReBAC可行性分析

Figure 1 Feasibility analysis of link prediction for ReBAC optimization

1.2 传统边预测方法

传统边预测方法主要包括启发式方法、潜在特征方法两类。

启发式方法使用简单而有效的节点相似性分数作为链接的可能性的度量标准，如公共邻居（CN，common neighbor）、RPR（rooted page rank）[30]等方法，其主要思路是首先假定满足预定义特征的两个节点存在边，再通过CN节点数量、Jaccard分数、Katz指数等方法计算特征值从而进行边预测。但是这些预先定义的特征表达能力有限，只能描述部分的、局部的图结构模式。因此，启发式方法一般用于同构图的边预测，很难应用于具有复杂形成机制的网络。

潜在特征方法通常以节点的潜在属性或表示为基础，通过矩阵分解[31]、网络嵌入[32]等方法实现边的预测。这些方法本质上是从图结构中提取低维节点嵌入信息，但不能捕捉节点之间的结构相似性[33]，即共享相同邻域结构的两个节点没有映射到相似的嵌入；潜在特征方法属于直推式学习方法，学习的节点嵌入不能推广到新节点或新网络。

1.3 基于GNN的边预测方法

随着图神经网络的发展，基于GNN的图表示学习应用于边预测中，取得了较好的效果。基于GNN的边预测方法分为基于节点的GNN方法和基于子图的GNN方法。

（1）基于节点的GNN方法

基于节点的GNN方法从图的局部邻域中学习节点嵌入，将GNN学习的成对的节点嵌入聚合为边的表示，如图自动编码器（GAE，graph auto encoder）、可变图自动编码器（VGAE，variational graph auto encoder）[18]、R-GCN[14]等模型。

此类方法分别独立计算两个目标节点的表示，没有考虑两个节点之间的相对位置、关联信息和公共邻居，从而造成聚合后的边表示结果出现偏差。此类方法的多数模型没有区分不同类别邻居节点的不同权重，不支持邻居节点重要程度的自动学习，从而影响边预测结果。

（2）基于子图的GNN方法

基于子图的GNN方法首先提取每个目标边周围的局部子图，然后对子图中节点计算标记，最后通过GNN学习子图表示边预测，如SEAL[15]、IGMC[34]、GraIL[16]等模型。Zhang等[15]通过衰变启发式理论验证了包围子图进行边预测的可行性，目标节点周围的局部子图充分考虑了节点、边以及它们周围邻居的拓扑结构特征。标记方法[15-16]可对目标节点及共同邻居节点之间的关联进行建模，从而比基于节点的GNN方法具有更好的边预测效果[35]。

但是，此类方法的很多模型提取的局部包围子图忽视了边的方向、类别（对应不同的关系类型）对图结构特征的影响，并且标记方法不支持对不同方向边所连接节点进行区分。SEAL模型只能处理无向简单图，未考虑边方向、多重边、关系类别等要素。多数模型只关注了图结构特征，没有考虑节点的属性特征信息，不能区分拓扑结构相同或相近、而节点特征不同的边。GraIL只通过学习拓扑结构信息进行边预测，忽视了不同类型、不同特征的节点对边预测结果的影响；TACT模型虽然综合考虑了图的拓扑结构和关系的相关性，但缺少对节点特征信息嵌入的学习，造成边预测结果准确性降低。

基于节点的GNN方法的输入数据是图节点特征信息（目标节点特征及其邻居节点特征信息），可以支持同质图节点、异质图节点特征信息，但不包括图结构信息。因此，在边预测时会损失节点之间的相对位置信息和结构关联信息。基于子图的GNN方法的输入数据是图结构特征信息（包围子图的结构、邻居节点结构信息），需要目标节点属于同一连通图。由于不包括图节点特征、边方向等信息，所以多数基于子图GNN方法的模型进行边预测时，只能支持同类型节点的无向图。

在基于子图GNN方法的基础上，需要增加边方向、边类型以及相关节点的特征信息等要素，用于提高基于图神经网络对实体关系图进行边预测的准确性，从而实现对访问控制规则所需实体关系的预测和补充。

2 基于GNN双源学习的边预测模型

2.1 问题定义

由于在大数据系统的访问控制场景中，实体与实体之间存在多种关系类型，本文将实体以及它们之间的关系定义为有向多重图(,,)，表示节点集合，表示有向边集合，表示关系集合。在中，节点∈，带有标签的有向边e=(,,) ∈，表示节点与之间存在标签为关系的边e，是e的头节点，是e的尾节点，∈表示一种关系类型。依据实体关系图与有向多重图之间的对应关系，可以将实体之间的关系预测问题转化为有向多重图的边预测问题，即预测有向多重图中的两个目标节点之间是否存在某种类型有向边的问题。

定义1 有向多重图的边预测：假设有向多重图(,,)中，目标节点、∈，判断节点、之间是否存在关系为的边e=(,,)的过程，被称为有向多重图的边预测。

2.2 模型框架

本文在基于子图的GNN方法的基础上，融入了边方向、边类型、节点特征等要素，融合了多关系特殊化处理方法，设计了基于图神经网络双源学习的边预测模型（LPMDLG，link prediction model based on dual-source learning of graph neural network）。LPMDLG框架如图2所示。

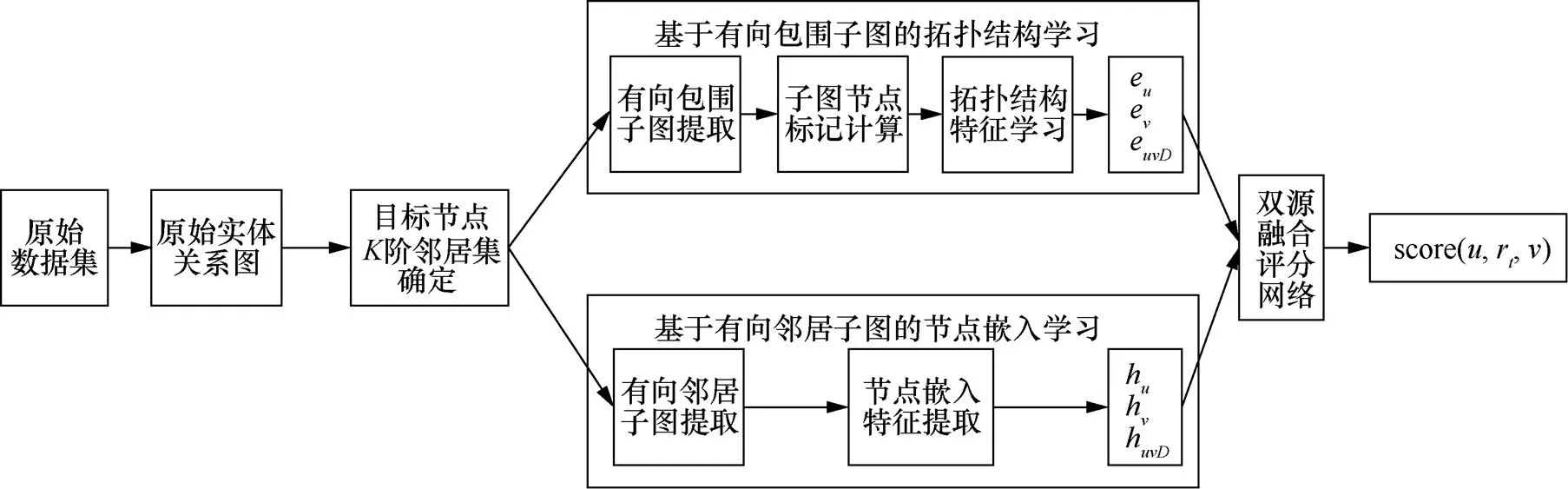
图2 LPMDLG框架

Figure 2 Framework of LPMDLG

第1步，由原始实体关系数据集生成原始实体关系图，如图3(a)所示。原始的实体关系数据集中的每个元素是一个由两个实体和对应关系组成的三元组，如<,,>表示实体与实体之间的关系为。将实体作为图节点，关系作为图节点之间的边，遍历集合中的每个三元组，可构建数据集对应的实体关系图。

第2步，确定实体关系图中目标节点和的阶邻居集。

第3步，基于GNN进行图表示学习，包括基于有向包围子图的拓扑结构学习与基于有向邻居子图的节点嵌入学习两个方法。基于有向包围子图的拓扑结构学习方法通过阶邻居集提取有向包围子图，计算子图中节点的标记值，基于节点标记值进行图卷积神经网络学习，生成节点与包围子图的拓扑结构特征。同步地，基于有向邻居子图的节点嵌入学习方法通过阶邻居集提取有向邻居子图，通过图卷积神经网络学习获得节点与邻居子图的嵌入特征。

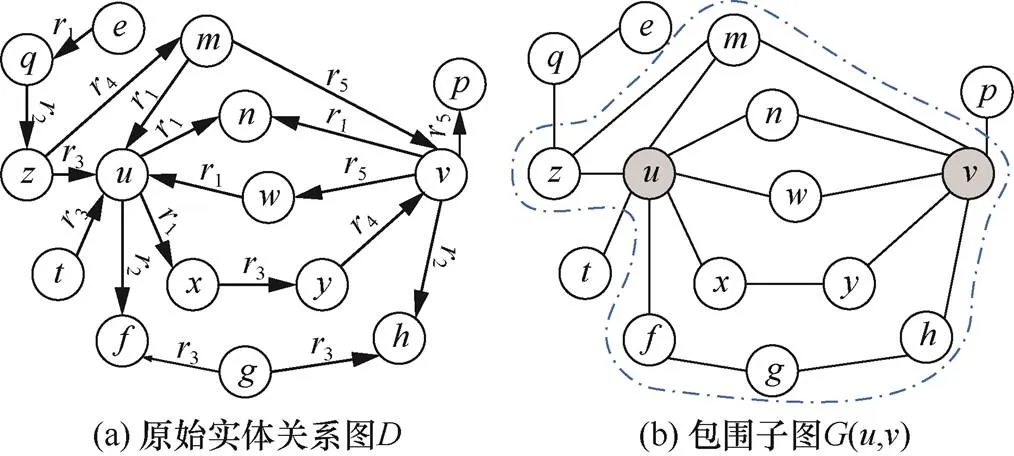
图3 原始实体关系图与包围子图示例

Figure 3 Example of original entityrelationship graph and enclosing subgraph

第4步，将两个方法学习的输出结果相结合，由评分网络进行综合打分，得到目标节点之间存在边（实体关系）的预测结果。

2.3 K阶邻居集的确定

确定目标节点的邻居集，是进行拓扑结构学习和节点嵌入学习的基础。本文提出了计算目标节点的阶邻居集的方法，过程如下。

1) 将原始实体关系图（有向多重图）转换为无向图，即为的底图[36]。

2) 基于广度优先算法，在底图中查找目标节点的跳邻居节点，构成节点的阶邻居集合N()，即底图中邻居节点到的距离不大于。通过同样方法得到节点的阶邻居集合N()。

2.4 基于有向包围子图的拓扑结构学习方法

基于有向包围子图的拓扑结构学习方法通过图神经网络学习目标节点及其有向包围子图的拓扑结构特征信息。该方法包括目标节点的有向包围子图提取、子图节点标记计算和拓扑结构特征学习3个环节。

2.4.1 有向包围子图提取

SEAL、GraIL等模型采用局部包围子图的方法对目标节点之间边的可能性进行分析和判断。其提取过程是：首先，计算两个节点和的邻居集合N()和N()，其中表示邻居的最大距离（无方向的）；其次，取N()和N()的交集，得到N()∩N()；最后，通过修剪孤立的或距离大于的节点来计算包围子图(,)（如图3(b)蓝色虚线所示）。

这种提取包围子图方法的不足包括两方面。一是提取目标节点的包围子图时没有考虑边的方向。所得到子图中的节点及其周围拓扑结构与有向图中的拓扑结构不完全相同，如图3(b)中，由于边是无向的，节点到节点、、可达，但实际的原始实体关系图（图3(a)）中，节点到节点单步可达，而节点到节点、不是单步可达的。基于该包围子图进行后续的节点标记与结构特征学习时，会出现节点的拓扑结构不同而标记相同的现象，无法区分不同方向的边所连接的节点，如图3(b)中不能区分节点、拓扑结构的不同。二是原始的包围子图没有区分边的不同类型（即不同的关系）。例如，图3(a)中，边e、e都是的接邻边，但两条边的类型不同，即所代表的实体关系属于不同类别，分别是关系1、2。原始的包围子图将上述两条边当作同一类别，如图3(b)中，边e、e的类型是相同的，那么在后续进行拓扑结构学习时，不能区分不同关系1、2对其产生的影响。

为克服上述不足，本文提出了有向包围子图提取方法。为了准确描述提取方法，本文对关键术语进行了如下定义。

定义2 路径：有向图中的一个路径path是一个由顶点x和边a交错排列的序列=11223…x−1a−1x，=1,2,…,−1,中边a的尾是顶点x，头是顶点x+1，并且任意两条边是不相同的，顶点互不相同，也称是一条从节点x到节点x的（1,x）路径。

定义3 可达、逆向可达：如果有向图中存在一条(,)路径，则称从节点到节点是可达的，节点到节点是逆向可达的。

定义4 距离：对于有向图的节点和，如果节点到节点是可达的，那么从节点到节点的距离(,)是路径(,)的最小长度，从节点到节点是逆向可达的，距离(,)=−(,)，否则记(,) = ∞。

定义5 底图距离：称有向图的底图中两个顶点x，x之间的距离d(,)为底图距离，定义为中最短路径的长度。如果此路径不存在，令d(,)=∞。

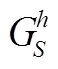
定义7 有向包围子图：对于一个有向多重图=(,,)，给定目标节点=｛,｝⊆，的阶有向包围子图是由中与节点和的底图距离不超过的节点集合组成的子图，记为D(,) =(V,E,R)。其中V={|d(,) ≤∩d(,) ≤}, 表示有向包围子图的节点集，E={(,)|,∈V}，表示其有向边集合，R⊆，表示其关系集合。

目标节点｛,｝的有向包围子图提取过程如下。

1) 在的底图中，求节点和的阶邻居集合的交集：N(,)=N() ∩N()。

2) 在中查找N(,)的节点关联的边及边类型（关系类别），获得其阶有向包围子图D(,) = (V,E,R)。如图4所示，红色虚线表示目标节点、的有向包围子图D(,)，它与包围子图的区别是边增加了边方向、边类型。

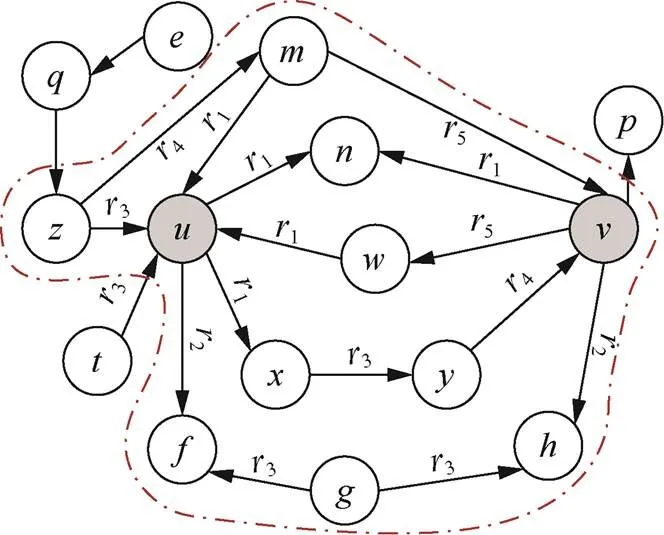
图4 有向包围子图DEK(u,v)

Figure 4 Directed enclosing subgraphD(,)

2.4.2 子图节点标记计算

SEAL、GraIL等模型采用了双半径节点标记（DRNL，double radius node labeling）方法对包围子图节点进行标记计算，作为拓扑结构学习的初始特征信息。Zhang等[35]证明了在边预测应用中，节点标记方法优于单纯的one-hot编码方法，前者更能准确地表示节点的图结构特征。DRNL不支持区分边的方向。假设有向图的两个节点在其底图（无向图）中是同构节点，由于关联的边的方向、关系类别的不同，原有向图的两个节点可能是非同构的。例如，图5(a)中根据DRNL方法，3个节点、是同构节点，标记均为（1,1），但实际上因为边的方向、类别不同，三者是不同构的，标记也不应该相同。

本文在DRNL方法的基础上，结合边的方向，提出了有向双半径节点标记（DDRNL，directed double radius node labeling）方法。如图5(b)所示，节点和有向包围子图中的每个节点用元组((,),(,))标记，记为()。其中(,)表示有向图的节点不经过到达的最短路径长度，(,)表示节点不经过到达的最短路径长度。该元组表示了每个节点相对于目标节点在有向包围子图中的结构位置。当到不可达时，(,)= ∞。同样，当到不可达时，(,)= ∞。目标节点和分别表示为（0,1）和（1,0）。

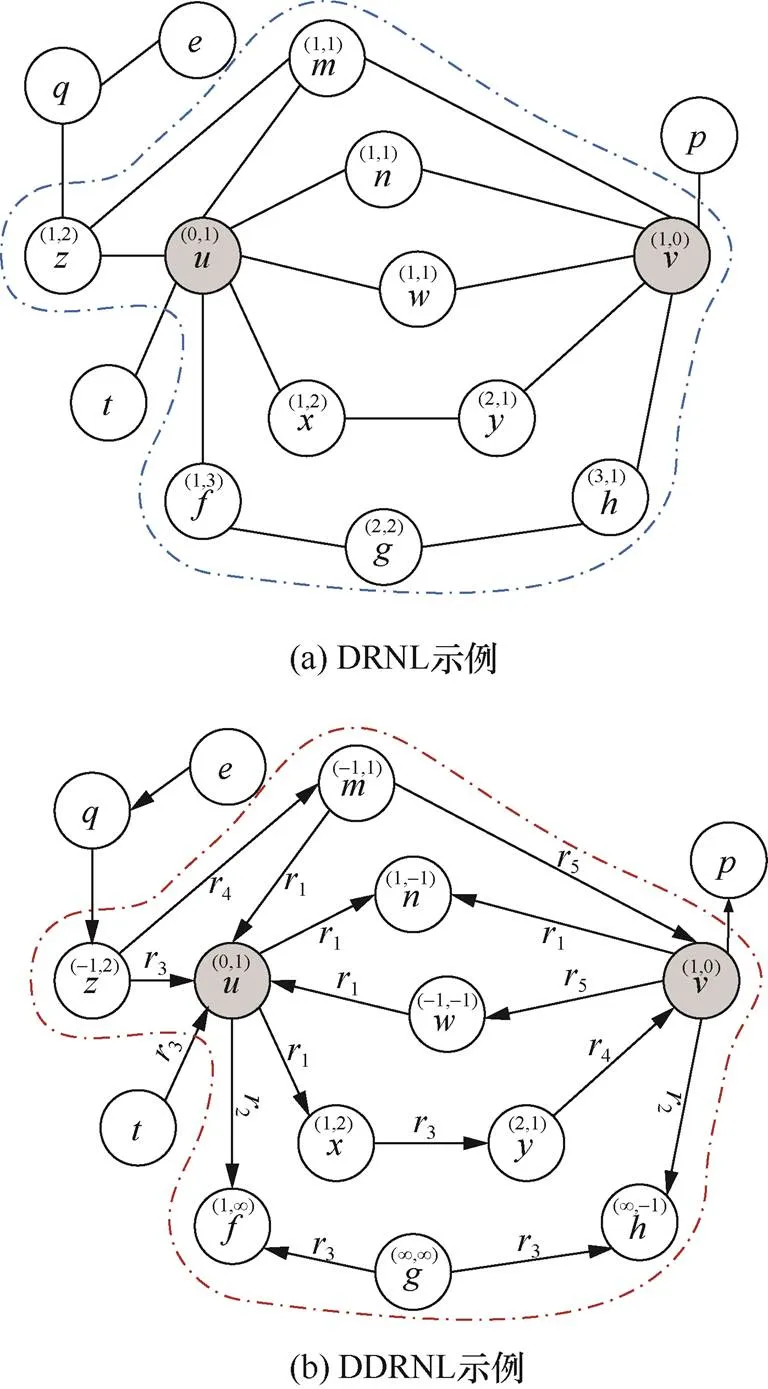
图5 DRNL、DDRNL对比示例

Figure 5 Comparison of DRNL, DDRNL examples

DDRNL方法的实现如算法1所示。

算法1 DDRNL

输入D(,)

输出(),∈D(,)，()=((,),(,))

1)()=((,),(,))=(0,1),()=((,),(,))=(1,0),()=(,),(∈D(,)，,)//节点标记初始化

2)(out,)=(in,)={}; //节点的可达队列和逆向可达队列

3)(out,)=(in,)={}; //节点的可达队列和逆向可达队列

4) {(,),∈(out,)}Label((out,),D(,))

5) {(,),∈(in,)}Label((in,),D(,))

6){(,),∈(out,)}Label((out,),D(,))

7) {(,),∈(in,)}Label((in,),D(,))

1) 节点标记初始化：目标节点和的标记分别表示为（0,1）、（1,0），D(,)中的其他节点标记为（∞,∞）。

2) 节点队列初始化：分别建立节点和的可达节点队列和逆向可达节点队列。out()表示节点的可达节点集合组成的队列，in()表示节点的逆向可达节点集合组成的队列。初始时，out()=in()=｛｝，其中=或。当=时，表示目标头节点的相关队列，当=时，表示目标尾节点的相关队列。

3) 计算节点可达节点的标记的第一元素：计算与其可达节点的距离(,)。

4) 计算节点逆向可达节点的标记的第一元素：计算与其逆向可达节点的距离(,)。

5) 计算节点可达节点的标记的第二元素：计算的可达节点到的距离(,)。

6) 计算节点逆向可达节点标记的第二元素：计算的逆向可达节点到的距离(,)。

第3)～6)步，调用了节点标记元素计算方法，如算法2所示。

算法2 节点标记元素计算

输入(dir,), D(,),dir={in,out},={,}

输出(),∈(,)()=((,),(,))

1) while(Empty((dir,))True)

2)= front((dir,))

3) for(in(dir,))

4) if(==,dir==out,and(,)==)

5)(,)=(,),pred()=, push ((dir,),)

6) if (==,dir==in, and(,)==)

7)(,)=(,)1,succ()=, push ((dir,),)

8) if(==,dir==out, and(,)==)

9)(,)=(,)1,pred()=, push ((dir,),)

10) if (==,dir==in, and(,)==)

11)(,)=(,)1,succ()=,push ((dir,),)

12) return

算法2的输入为目标节点的可达或逆向可达节点队列、有向封闭子图D(,)，输出为节点标记元素值((,),(,))，∈(,)。

1) 当(dir,)不为空时，执行第一层循环。

2) 从(dir,)取出队列首部的节点，根据dir取值获得可达（dir=out）或逆向可达（dir=in）的直接邻居节点集合(dir,)。

3) 通过第二层循环，从(dir,)中依次取出的直接邻居节点，分情况计算节点的标记元素值。

①如果是目标头节点的可达节点队列（=,dir=out），且到的距离为，则令(,)=(,)1，节点的前缀节点为节点，即pred()=，并把节点加入(dir,)的队尾。

②如果是目标头节点的逆向可达节点队列（=, dir=in），且到的距离为，则令(,)=(,)−1，节点的后继节点为节点，即succ()=，并把节点加入(dir,)的队尾。

③如果是目标头节点的可达节点队列（=,dir=out），且到的距离为，则令(,)=(,)−1，节点的前缀节点为节点，即pred()=，并把节点加入到(dir,)的队尾。

④如果是目标头节点的逆向可达节点队列（=, dir=in），且到的距离为，则令(,)=(,)+1，节点的后继节点为节点，即succ()=，并把节点加入(dir,)的队尾。

节点，(,)=0，dir=out，从(out,)取出队列首部的节点（此时=），直接邻居节点集合(out,)={,,}，令=，(,)=(,)+1=1，pred()=，加入(out,)；令=，(,)=(,)+1=1，pred()=，加入(out,)；令=，(,)=(,)+1=1，pred()=，加入(out,)；此时(out,)={,,}。取出(out,)的队首节点(out,)=Null，取出队首节点，(out,)={}，令=，(,)=(,)+1=2，pred()=，加入(out,)。同理计算可得：(,)=1，(,)=(,)=(,)=−1，(,)=(,)=1，(,)=(,)=(,)=1，(,)=(,)=2，(,)=(,)=(,)=(,)=。

2.4.3 拓扑结构特征学习

本文在R-GCN、SEAL、GraIL模型的基础上，设计了基于边方向与边类别的图神经网络的消息传递网络。先按照边的类别（关系）对邻居节点分别进行聚合；再将节点当前的拓扑结构信息与聚合结果相结合来迭代更新节点信息；最后综合有向封闭子图内各个节点的输出结果，分别得到目标节点和有向包围子图的拓扑结构特征信息。拓扑结构特征学习的图神经网络示意如图6所示。

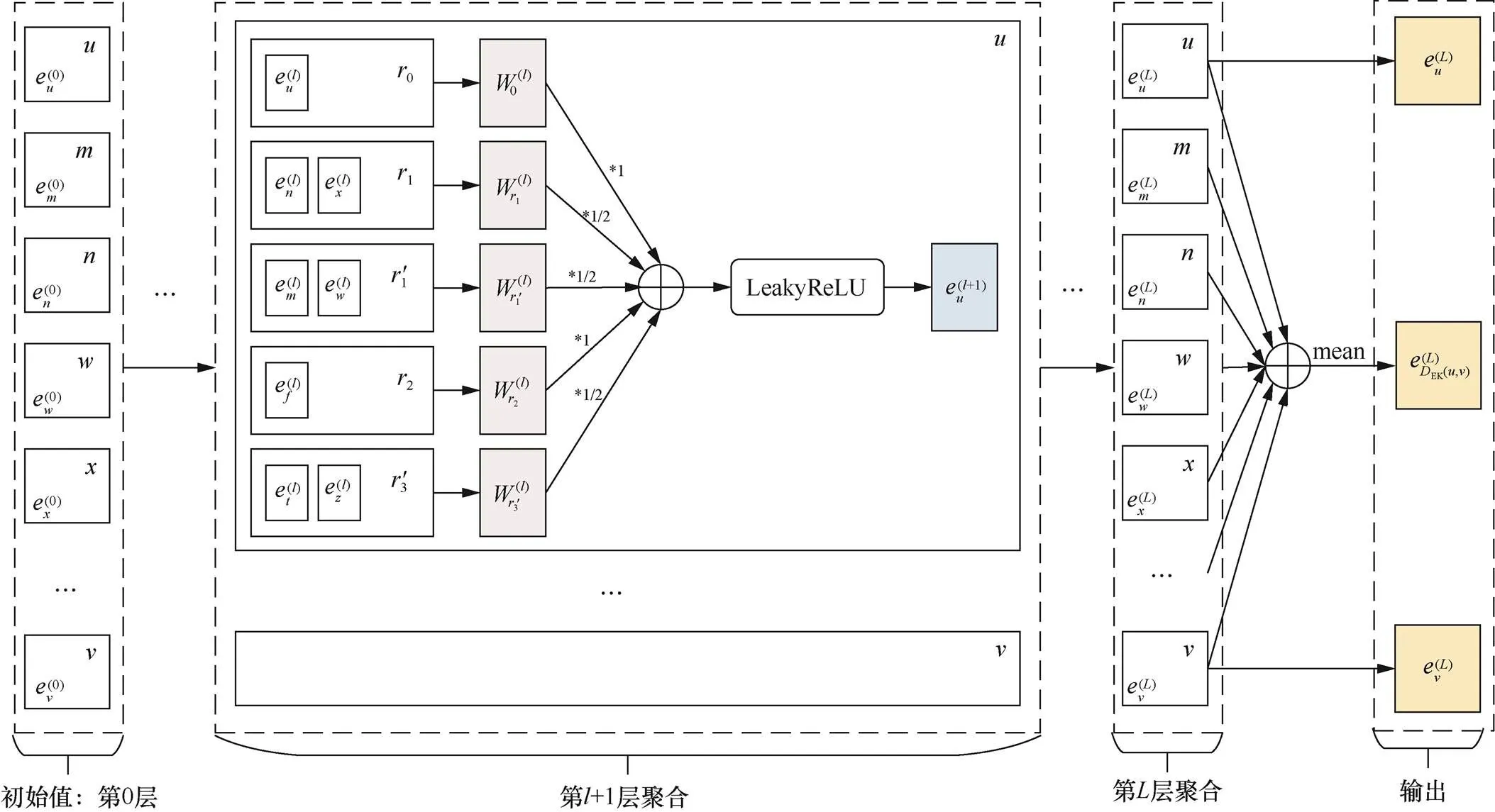
图6 拓扑结构特征学习的图神经网络示意

Figure 6 Graph neural network for topology feature learning

假设两个节点之间存在0～个边类型（关系类别）。按照不同的边类型分别进行聚合，每个节点的层的图结构特征输出为：

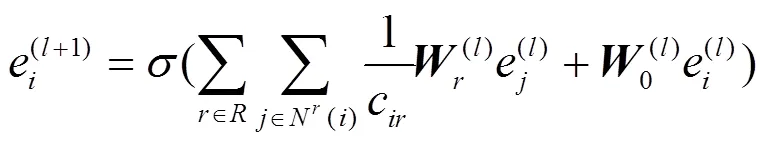
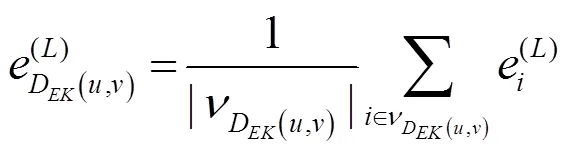
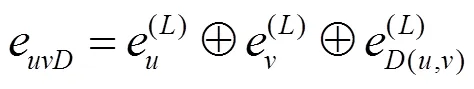
2.5 基于有向邻居子图的节点嵌入学习方法

基于有向邻居子图的节点嵌入学习方法通过图神经网络实现信息的逐层传递，将节点各类型邻居节点嵌入特征的聚合结果与其当前层的嵌入特征相结合，迭代更新下一层的节点嵌入特征，并将注意力系数、边的多种关系与聚合运算相结合，自动学习各类关系对应邻居节点对于目标节点的重要性的权重。该方法包括有向邻居子图提取和节点嵌入特征学习两个环节。

2.5.1 有向邻居子图提取

为解决节点嵌入特征学习的过平滑问题，本文提取目标节点的阶邻居节点，合并组成有向邻居子图，以限定节点特征学习的邻居节点范围。

定义8 有向邻居子图：对于一个有向多重图=(,,)，给定目标节点=｛,｝⊆，的阶有向邻居子图是由中与节点或的底图距离不超过的节点集合组成的子图，记为D(,) =(V,E,R)。其中，V={|d(,)≤∪d(,) ≤}，表示有向邻居子图的节点集，E={(,)|,∈V}，表示其有向边集合，R⊆，表示其关系集合。

有向邻居子图提取方法过程如下。

1) 在有向图的底图中，获取节点和的阶邻居集合N()N()，计算它们的并集N'(,)=N()∪N()。

2) 在有向图中查找N'(,)的节点关联的边及其关系类别，获得其有向邻居子图D(,)=(V,E,R)，V=N'(,)。有向邻居子图提取如图7(a)所示，虚线表示目标节点、的有向邻居子图。

2.5.2 节点嵌入特征学习

节点嵌入特征学习环节在R-GCN模型的基础上，针对不同种类的关系进行了特化处理，即按照不同的关系采用，并通过注意力系数[37]对同类型关系下不同邻居的重要程度进行自动学习。每个节点的输出特征为

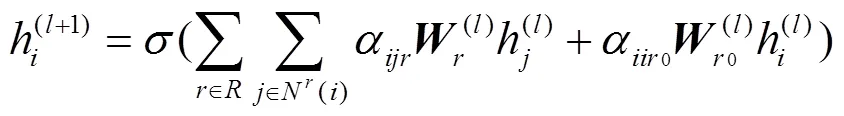
图7 有向邻居子图提取与节点嵌入特征学习示例

Figure 7 Example of directed neighbor subgraph extraction and node embedding feature learning

注意力系数为

归一化注意力系数为

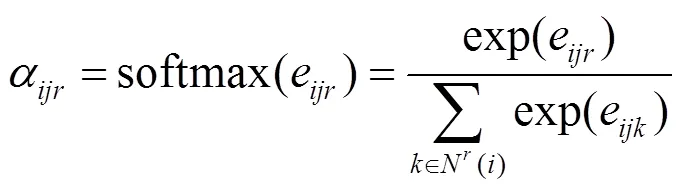
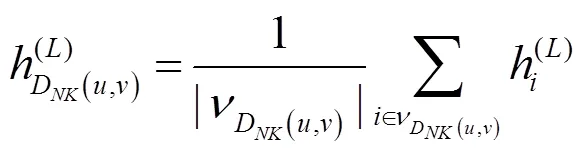
目标节点和及其有向邻居子图的嵌入特征信息输出为

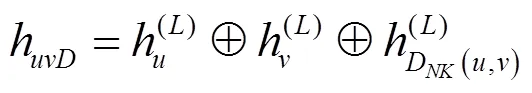
2.6 双源融合的评分网络与训练

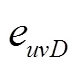
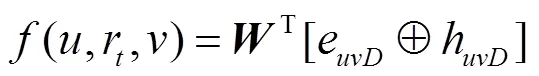
在学习过程中，本文采用噪声对比铰链损失函数训练模型，使正三元组的得分高于负三元组。对于训练图中出现的每个三元组，通过用均匀采样的随机实体替换三元组的头部节点或尾部节点来采样得到负三元组。然后使用损失函数通过随机梯度下降来训练模型。损失函数为

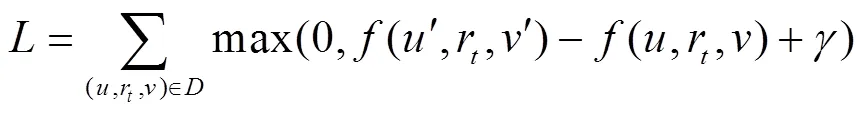
3 实验分析

3.1 数据集

为验证LPMDLG模型进行边预测的效果，综合R-GCN、SEAL、GraIL、TACT模型实验结果，本文选用标准的WN18RR[38]、FB15k-237[39]和NELL-995[40]3个数据集各自的两个版本（v2、v3）作为基准测试，采用文献中的比例将数据集划分为训练集、测试集。描述数据集的参数为实体数量#E、关系数量#R、三元组数量#TR[17]。

为验证边预测结果对自动化动态授权、简化匹配ReBAC规则的效果，本文选用ReBAC模型基准测试数据集[9]（EMR_15、healthcare_5、Project-mgmt_5、University_5、e-document_175和eWorkforce_30共6个数据集）作为ReBAC规则匹配的基准测试数据。

3.2 基线模型与实验参数

根据现有工作的研究与对比，本文选择4个模型作为边预测的基线模型，包括基于节点的模型R-GCN，基于子图的模型SEAL、GraIL、TACT。评估指标为AUC-PR、MRR（mean reciprocal ranking）、Hits@。

边预测基线模型保持超参数与原始文献相同，本文采用Adam optimizer优化器，拓扑结构学习中随机采样两阶邻居建立有向包围子图，节点嵌入学习选择两层邻居建立有向邻居子图。对于WN18RR、FB15k-237、NELL-995，损失函数中的margins分别设置为8、16、10。训练周期epochs的最大数量被设置为10。

ReBAC规则匹配基线模型采用DTRM（decision tree ReBAC miner）模型[9]，分别在边预测前、预测后两个阶段对数据集进行ReBAC规则提取与匹配。通过比较两个阶段的匹配结果验证本文LPMDLG对实体的自动化动态授权、简化匹配ReBAC规则的效果。

3.3 实验结果

3.3.1 AUC-PR

为提高对比的公平性，本文参照GraIL、TACT模型的实验采样方法，使用AUC-PR作为分类度量。AUC-PR表示精确召回曲线（P-R，precision recall curve）的下方面积，可看作为每个Recall阈值计算的Precision的平均值。首先，为获得相应的负样本，本文用随机采样实体替换测试数据子集中三元组的头节点或者尾节点；然后，对具有相同数量的负三元组的正三元组进行评分；最后计算AUC-PR。本文用不同的随机种子将每个实验运行3次，并计算平均结果。

表1显示了各个模型进行边预测的AUC-PR结果。*表示数据通过图神经网络框架（DGL）中的模型源码执行所得，**表示数据来自TACT。本文提出的模型——LPMDLG在大多数数据集上优于其他模型，特别是对于关系数量#R较多的数据集，如FB15k-237数据集、NELL-995数据集的v2、v3版本等，AUC-PR值平均提高约0.65%。

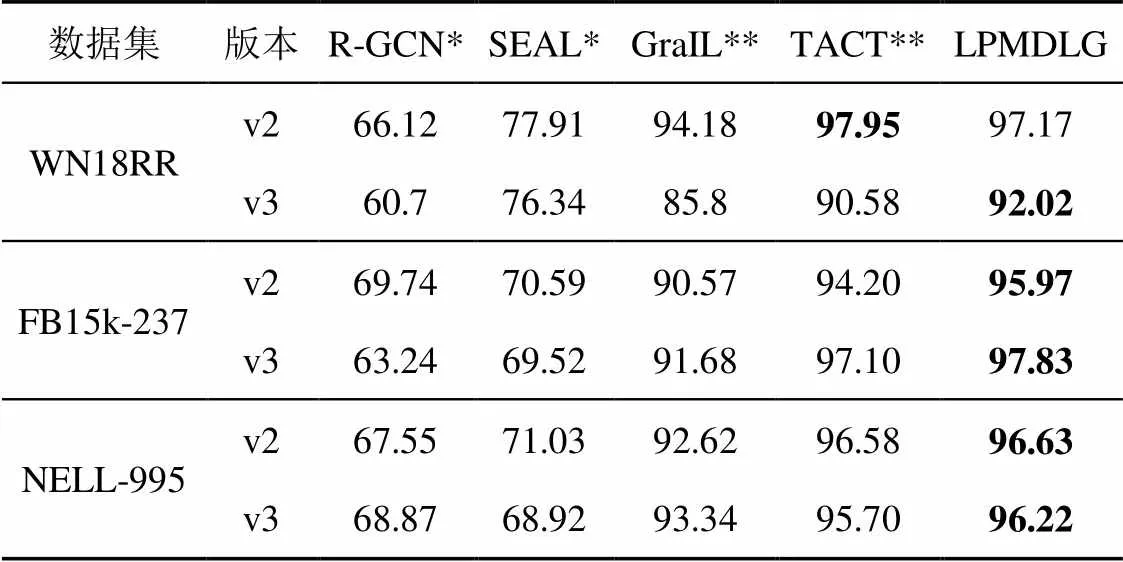
表1 AUC-PR结果

LPMDLG的AUC-PR值优于其他模型，主要是由于它采用了基于拓扑结构和节点嵌入相结合的双源信息学习模式进行边的预测。与R-GCN相比，LPMDLG对不同关系、类型的邻居节点，采用注意力机制学习其重要程度，赋予其不同的权重。与SEAL相比，LPMDLG针对拓扑结构学习、节点嵌入学习两种模式选用了不同的邻居集，并且在该模型的拓扑结构学习中采用了新标记方法，该方法考虑边的不同方向对其标记结果的影响。与GraIL、TACT模型相比，LPMDLG增加了对节点特征的学习，采用了新标记方法，考虑边的方向对其影响，并对注意力学习机制进行了简化。实验结果说明了本文提出的通过拓扑结构与节点嵌入相结合进行边预测方法的有效性。

3.3.2 MRR和Hits@

本文进一步通过排名度量评估边预测模型LPMDLG，选择MRR和Hits@作为评价指标，验证模型进行多关系数据集边预测的有效性。二者的计算过程如下。

首先，将测试集的每个三元组(,r,)中的r依次替换为数据集的每种关系；其次，通过评分函数分别计算替换后对应的分数值；然后，将得到一系列的分数进行排序，得到该三元组的边预测排序；对各个三元组的边预测正确结果的排名，求其倒数的平均值得到MRR值；判断每个三元组正确结果的排名是否不超过，最后排在前的个数与总数的比值就是Hits@。

表2、表3分别显示了各个模型的MRR和Hist@1（取=1）结果。其中，*表示数据通过图神经网络框架中的模型源码执行所得，**表示数据来自TACT。

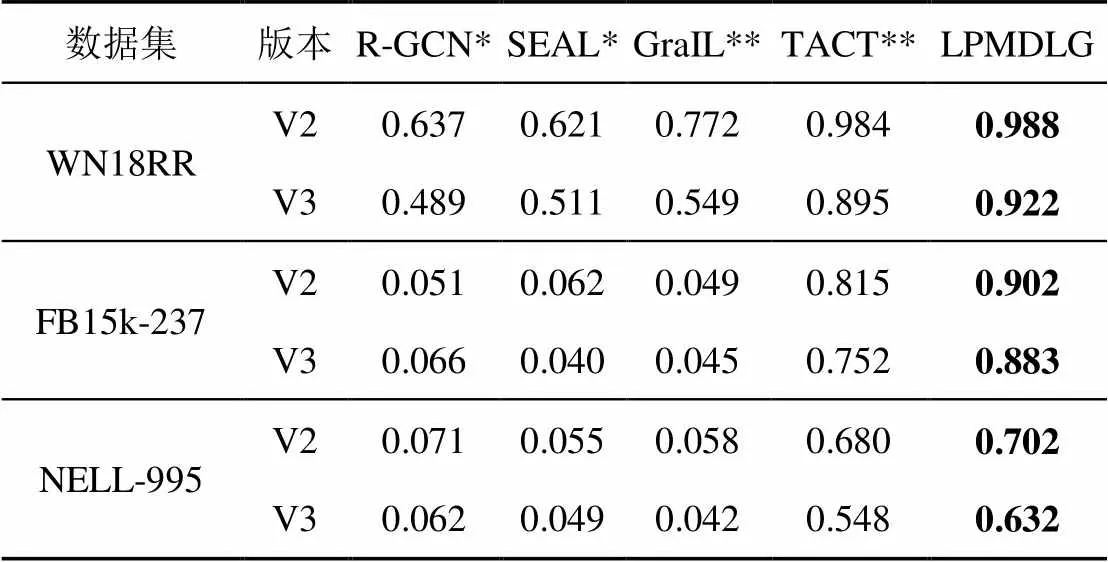
表2 MRR结果

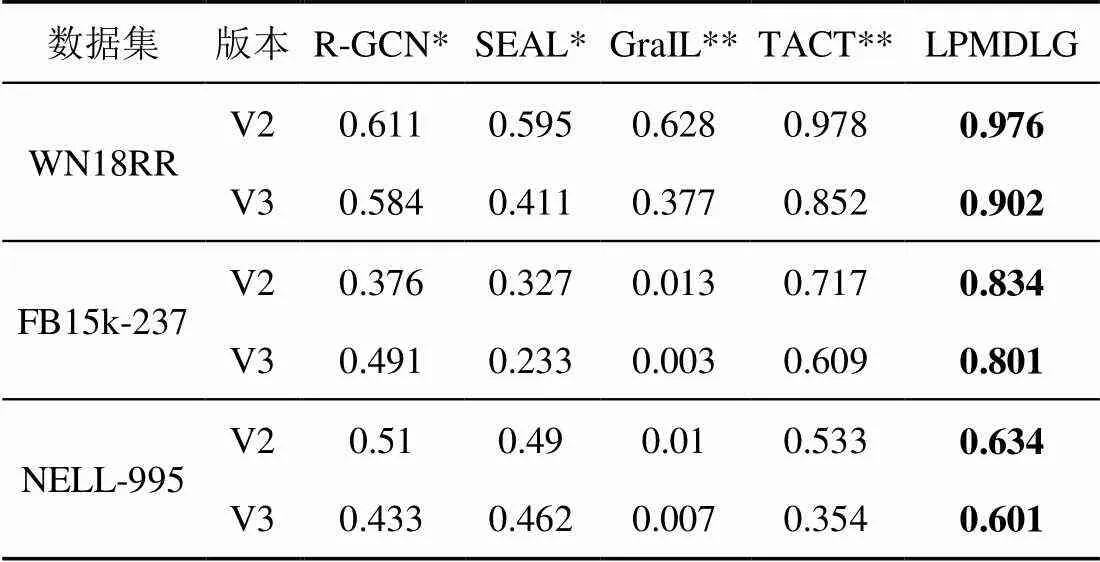
表3 Hits@1结果

实验结果表明，LPMDLG的MRR和H@1指标优于基线参考模型，其中对于包含更多关系类型数据集FB15k-237和NELL995，MRR和H@1指标提高更加明显。这是由于LPMDLG从3个方面提高了边预测的能力：一是基于拓扑结构和节点嵌入特征双源信息学习，比单一模式学习的结果更能全面地反映目标节点与边的特征信息；二是模型在学习拓扑结构时增加了边方向、边类型等要素，可实现对不同关系类别的区分；三是模型在学习节点嵌入特征时综合了边的方向（关系指向）、边的类别（关系类别）、邻居权重等因素进行学习，输出结果更能反映出不同关系之间的区别。另外，数据集FB15k-237和NELL-995比WN18RR包含更多的关系，实验结果说明LPMDLG对于关系数量较多的数据集进行边预测更有优势，其更适用于多关系类型情况下的实体关系预测。

3.3.3 消融实验

3.3.4 ReBAC规则匹配结果

为验证边预测结果对实体自动化动态授权、简化匹配ReBAC规则的关系路径的效果，本文通过ReBAC规则匹配[9,11]实验进行分析。

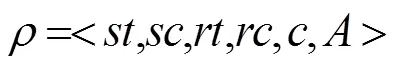
当SRA匹配规则时，主体可以依据规则对客体进行访问行为，则三元组取值为真，记为SRA=T。因此，满足ReBAC规则的三元组数量可表示为SRA=T的元组数量。

本文对EMR、healthcare等6个数据集[9]进行关系预测学习，分别统计关系预测前、预测后各个数据集规则匹配开销、满足ReBAC规则SRA数量的变化。

表4 LPMDLG模型消融实验结果对比

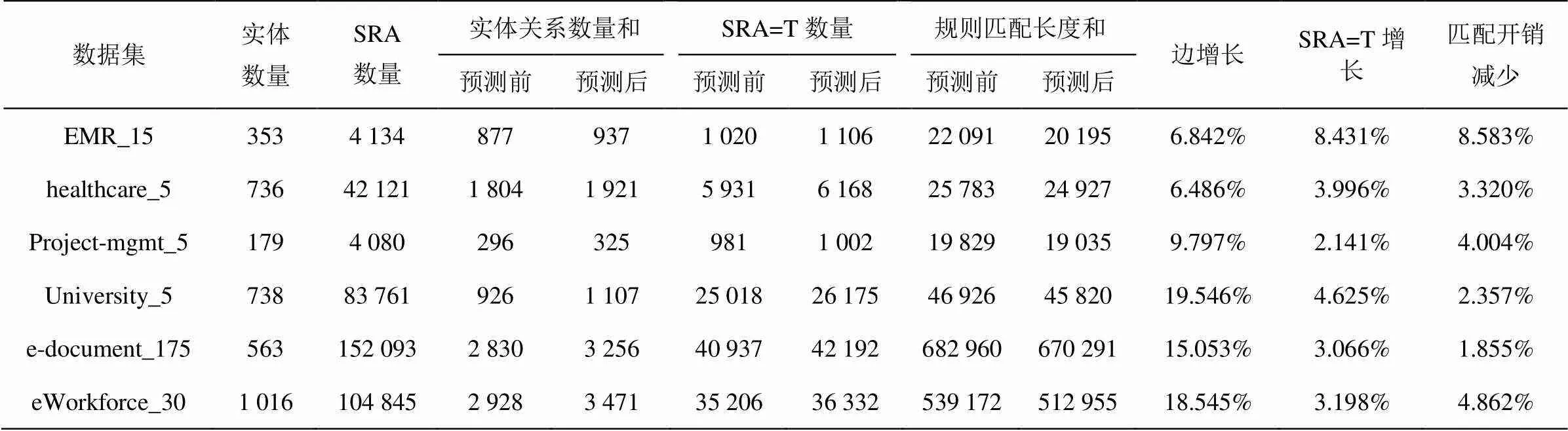
表5 关系预测前后SRA=T的数量、规则匹配开销变化

从表5可以看出，通过边预测，各个数据集的实体关系数量都有所增加，SRA=T的元组数量随之增加，表明满足规则的元组增加，在关系预测之前没有权限、权限不确定的主体获得了对目标资源的访问权限，从而验证了通过边预测实现了对某些SRA元组的自动授权。规则匹配长度之和随着实体关系数量的增加而减少，表明匹配ReBAC规则的路径得到了简化。这是由于采用LPMDLG模型后，发现并预测了原有数据集潜在的实体间的关系，对缺失的实体关系进行了有效的补充，原先没有访问权限的主体与目标客体之间建立了访问权限关系，并且对原先较为复杂的关系路径进行了简化，缩短了匹配ReBAC规则的关系路径。

4 结束语

本文将大数据访问控制中面临的实体关系预测问题转化为有向多重图的边预测问题，提出了基于图神经网络双源学习的边预测模型—— LPMDLG。与现有边预测模型（如R-GCN、SEAL、GraIL等）相比，所提模型采用了基于有向包围子图的拓扑结构学习方法，加入了边方向、边类型等要素，提高了节点拓扑结构特征的准确性；该模型采用了基于邻居子图的节点嵌入学习方法，融入注意力系数与关系类型学习多关系节点特征，提高了节点嵌入特征的表示能力；该模型采用了基于拓扑结构和节点嵌入相融合的双源学习模式，优于单一模式的边预测效果。实验结果表明本文提出的模型在多关系的有向多重图的边预测中提高了预测结果，验证了该模型适用于解决大数据访问控制系统中实体关系预测问题。后续将进一步研究该模型中拓扑结构与节点嵌入的并行学习方法，以降低模型训练时间，并且研究基于关系预测结果的ReBAC规则推理问题，从而实现基于实体关系的大数据动态、自动化访问控制。

[1] 李昊, 张敏, 冯登国, 等. 大数据访问控制研究[J]. 计算机学报, 2017, 40(1): 72-91.

LI H, ZHANG M, FENG D G, et al. Research on access control of big data[J]. Chinese Journal of Computers, 2017, 40(1): 72-91.

[2] FONG P W L. Relationship-based access control: protection model and policy language[C]//Proceedings of the First ACM Conference on Data and Application Security and Privacy. 2011: 191-202.

[3] AHMED T, SANDHU R, PARK J. Classifying and comparing attribute-based and relationship-based access control[C]//Proceed- ings of the Seventh ACM on Conference on Data and Application Security and Privacy. 2017: 59-70.

[4] BOGAERTS J, DECAT M, LAGAISSE B, et al. Entity-based access control: supporting more expressive access control policies[C]//Proceedings of the 31st Annual Computer Security Applications Conference. 2015: 291-300.

[5] CHAKRABORTY S, SANDHU R. On Feasibility of attribute- aware relationship-based access control policy mining[C]//IFIP International Federation for Information Processing 2021. 2021: 393-405.

[6] CHAKRABORTY S, SANDHU R. Formal analysis of ReBAC policy mining feasibility[C]//Proceedings of the Eleventh ACM Conference on Data and Application Security and Privacy(CODASPY '21). 2021: 197-207.

[7] HU V C, FERRAIOLO D, KUHN R, et al. Guide to Attribute based access control (ABAC) definition and considerations: NIST Special Publication 800-162[S]. 2019: 1-37.

[8] BUI T, STOLLER S D, LI J J. Greedy and evolutionary algorithms for mining relationship-based access control policies[J]. Computers & Security, 2019, 80: 317-333.

[9] BUI T, STOLLER S D. A decision tree learning approach for mining relationship-based access control policies[C]//Proceedings of the 25th ACM Symposium on Access Control Models and Technologies. 2020: 167-178.

[10] BUI T, STOLLER S D, LI J. Mining relationship-based access control policies from incomplete and noisy data[M]//Foundations and Practice of Security. Switzerland. 2019: 267-284.

[11] BUI T, STOLLER S D. Learning attribute-based and relationship-based access control policies with unknown values[C]//Information Systems Security - 16th International Conference(ICISS). 2020: 23-44.

[12] IYER P, MASOUMZADEH A. Active learning of relationship-based access control policies[C]//Proceedings of the 25th ACM Symposium on Access Control Models and Technologies. 2020: 155-166.

[13] ZHANG M. Graph neural networks: link prediction[M]//Graph Neural Networks: Foundations, Frontiers, and Applications. Singapore, Springer. 2021: 195-224.

[14] SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling relational data with graph convolutional networks[C]//The Semantic Web. 2018: 593-607.

[15] ZHANG M, CHEN Y. Link prediction based on graph neural networks[C]//Proceedings of 32nd Conference on Neural Information Processing Systems (NIPS 2018). 2018: 1-11.

[16] TERU K K, DENIS E, HAMILTON W L. Inductive relation prediction by subgraph reasoning[C]//Proceedings of the 37th International Conference on Machine Learning(ICML). 2020: 1-10.

[17] CHEN J, HE H, WU F, et al. Topology-aware correlations between relations for inductive link prediction in knowledge graphs[C]//Pro- ceedings of 35th AAAI Conference on Artificial Intelligence. ELECTR NETWORK. 2021: 6271-6278.

[18] KIPF T N, WELLING M. Variational graph auto-encoders[C]//Bay- esian Deep Learning Workshop (NIPS 2016). 2016: 1-3.

[19] YOU J, YING R, LESKOVEC J. Position-aware graph neural networks[C]//Proceedings of 36th International Conference on Machine Learning (ICML). 2019: 7134-7143.

[20] CHAMI I, YING R, RÉ C, et al. Hyperbolic graph convolutional neural networks[J]. Advances in Neural Information Processing Systems, 2019, 32: 4869-4880.

[21] LI P, WANG Y B, WANG H W, et al. Distance encoding: design provably more powerful neural networks for graph representation learning[J]. arXiv: 2009.00142, 2020.

[22] LIBEN-NOWELL D, KLEINBERG J. The link prediction problem for social networks[J]. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031.

[23] ADAMIC L A, ADAR E. Friends and neighbors on the Web[J]. Social Networks, 2003, 25(3): 211-230.

[24] SHIBATA N, KAJIKAWA Y, SAKATA I. Link prediction in citation networks[J]. Journal of the American Society for Information Science and Technology, 2012, 63(1): 78-85.

[25] STANFIELD Z, COŞKUN M, KOYUTÜRK M. Drug response prediction as a link prediction problem[J]. Scientific Reports, 2017, 7: 40321.

[26] NICKEL M, MURPHY K, TRESP V, et al. A review of relational machine learning for knowledge graphs[J]. Proceedings of the IEEE, 2016, 104(1): 11-33.

[27] CRAMPTON J, SELLWOOD J. Path conditions and principal matching: A new approach to access control[C]//Proceedings of the 19th ACM Symposium on Access Control Models and Technologies (SACMAT’14). 2014: 187-198.

[28] PACI F, SQUICCIARINI A, ZANNONE N. Survey on access control for community-centered collaborative systems[J]. ACM Computing Surveys, 2019, 51(1): 1-38.

[29] ASIM Y, MALIK A K. A survey on access control techniques for social networks[M]//Information Diffusion Management and Knowledge Sharing. IGI Global, 2020: 319-342.

[30] BRIN S, PAGE L. Reprint of: the anatomy of a large-scale hypertextual Web search engine[J]. Computer Networks, 2012, 56(18): 3825-3833.

[31] OU M D, CUI P, PEI J, et al. Asymmetric transitivity preserving graph embedding[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining(KDD ’16). 2016: 1105-1114.

[32] PEROZZI B, AL-RFOU R, SKIENA S. Deepwalk: online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data mining(KDD'14). 2014: 701-710.

[33] RIBEIRO L, SAVERESE P, FIGUEIREDO D R. Struc2vec: learning node representations from structural identity[C]//The ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2017: 385-394.

[34] ZHANG M H, CHEN Y X. Inductive matrix completion based on graph neural networks[J]. arXiv: 1904.12058, 2019.

[35] ZHANG M, LI P, XIA Y, et al. Labeling trick: a theory of using graph neural networks for multi-node representation learning[C]//35th Conference on Neural Information Processing Systems (NeurIPS 2021). 2022: 9061-9073.

[36] BANG-JENSEN J, GUTIN G. Digraphs theory, algorithms and applications (second edition) [M]. London: Springer-Verlag, 2007.

[37] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[J]. arXiv: 1710.10903, 2017.

[38] TOUTANOVA K, CHEN D J. Observed versus latent features for knowledge base and text inference[C]//Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality(CVSC). 2015: 57.

[39] DETTMERS T, MINERVINI P, STENETORP P, et al. Convolutional 2D knowledge graph embeddings[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2018: 1811-1818.

[40] XIONG W, HOANG T, WANG W Y. DeepPath: a reinforcement learning method for knowledge graph reasoning[C]//Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing(EMNLP). 2017: 564-573.

Access control relationship prediction method based on GNN dual source learning

SHAN Dibin, DU Xuehui, WANG Wenjuan, LIU Aodi, WANG Na

Information Engineering University, Zhengzhou 450001, China

With the rapid development and wide application of big data technology, users’ unauthorized access to resources becomes one of the main problems that restrict the secure sharing and controlled access to big data resources. The ReBAC (Relationship-Based Access Control) model uses the relationship between entities to formulate access control rules, which enhances the logical expression of policies and realizes dynamic access control. However, It still faces the problems of missing entity relationship data and complex relationship paths of rules. To overcome these problems, a link prediction model LPMDLG based on GNN dual-source learning was proposed to transform the big data entity-relationship prediction problem into a link prediction problem with directed multiple graphs. A topology learning method based on directed enclosing subgraphs was designed in this modeled. And a directed dual-radius node labeling algorithm was proposed to learn the topological structure features of nodes and subgraphs from entity relationship graphs through three segments, including directed enclosing subgraph extraction, subgraph node labeling calculation and topological structure feature learning. A node embedding feature learning method based on directed neighbor subgraph was proposed, which incorporated elements such as attention coefficients and relationship types, and learned its node embedding features through the sessions of directed neighbor subgraph extraction and node embedding feature learning. A two-source fusion scoring network was designed to jointly calculate the edge scores by topology and node embedding to obtain the link prediction results of entity-relationship graphs. The experiment results of link prediction show that the proposed model obtains better prediction results under the evaluation metrics of AUC-PR, MRR and Hits@compared with the baseline models such as R-GCN, SEAL, GraIL and TACT. The ablation experiment results illustrate that the model’s dual-source learning scheme outperforms the link prediction effect of a single scheme. The rule matching experiment results verify that the model achieves automatic authorization of some entities and compression of the relational path of rules. The model effectively improves the effect of link prediction and it can meet the demand of big data access control relationship prediction.

big data, relationship-based access control, link predication, graph neural network

TP309

A

10.11959/j.issn.2096−109x.2022062

2022−06−01；

2022−08−15

杜学绘，office_paper@163.com

国家重点研发计划（2018YFB0803603，2016YFB0501904）；国家自然科学基金（62102449）；河南省重点研发与推广专项（222102210069）

The National Key R&D Program of China(2018YFB0803603, 2016YFB0501904), The National Natural Science Foundation of China (62102449), The Key Research and Development and Promotion Program of Henan Province(222102210069)

单棣斌, 杜学绘, 王文娟, 等. 基于GNN双源学习的访问控制关系预测方法[J]. 网络与信息安全学报, 2022, 8(5): 40-55.

Format: SHAN D B, DU X H, WANG W J, et al. Access control relationship prediction method based on GNN dual source learning[J]. Chinese Journal of Network and Information Security, 2022, 8(5): 40-55.

单棣斌（1982−），男，河北邯郸人，信息工程大学讲师，主要研究方向为大数据安全、信任安全、图神经网络。

杜学绘（1968−），女，河南新乡人，博士，信息工程大学教授、博士生导师，主要研究方向为信息系统安全、大数据和区块链安全。

王文娟（1981−），女，河南鹤壁人，博士，信息工程大学教授，主要研究方向为云计算安全、入侵防御。

刘敖迪（1992−），男，黑龙江伊春人，博士，信息工程大学讲师，主要研究方向为大数据安全。

王娜（1980−），女，山西临汾人，博士，信息工程大学副教授，主要研究方向为信息系统安全、大数据和区块链安全。