基于BRLWE的物联网后量子加密技术研究

高艺恬，陈立全，屠天扬，高原，陈芊叶

基于BRLWE的物联网后量子加密技术研究

高艺恬，陈立全，屠天扬，高原，陈芊叶

（东南大学网络空间安全学院，江苏 南京 210096）

随着量子计算机的发展，现有的公钥加密体系无法保障物联网通信的安全性。后量子加密算法所基于的数学难题目前还不能被量子计算机攻破，因此具备良好的抗量子安全性，尤其是基于格的公钥密码体制，有望成为下一代公钥加密体系的主流。然而，后量子加密算法存在计算量大、存储空间大等问题，如果将其直接应用于物联网终端的轻量级设备中，会降低物联网环境的通信效率。为了更好地保护物联网通信安全，保障物联网通信效率，提出了Sym-BRLWE（symmetrical binary RLWE）后量子加密算法。该算法在基于二进制环上容错学习（BRLWE，binary ring-learning with errors）问题的加密算法的基础上，改进了离散均匀分布上的随机数选取方式和多项式乘法的计算方式，从而满足物联网通信的效率要求，增加了加密安全性防护性措施以保证算法在取得高效率的同时具有高安全性，更加适应于物联网轻量设备。安全性分析表明，Sym-BRLWE加密算法具有高安全性，从理论上能够抵抗格攻击、时序攻击、简单能量分析和差分能量分析；仿真实验结果表明，Sym-BRLWE加密算法具有通信效率高的优势，加密解密效率高且密钥尺寸小，在模拟8 bit微型设备的二进制运算环境下，选择140 bit的抗量子安全级别参数时，相较于其他已有的基于BRLWE的加密算法，同等加密条件下Sym-BRLWE加密算法能够在加密总时间上减少30%～40%。

后量子密码；物联网；公钥加密；基于格的加密；环上容错学习问题

0 引言

网络安全问题不仅影响着人们的数据隐私，也关乎国家与社会的利益。互联网通信安全保障的基础在于信息加密技术的安全性。信息加密正面临着两大难题：一是物联网的蓬勃发展引发了物联网终端电子设备的应用热潮，给信息加密带来了极大的需求和挑战[1]；二是量子计算机的横空出世降低了处理海量数据的难度，给传统加密算法带来了致命的威胁[2]。传统的公钥加密技术已被证明无法抵御量子计算的攻击，量子计算机的产生导致现有密码体制不再安全。有专家预估在不久的将来，大规模量子计算机的商用将伴随着6G时代一起到来[3]。面对量子计算对加密领域造成的威胁，后量子密码应运而生。后量子加密算法具有抗量子性，可以弥补传统加密算法无法抵御量子攻击的不足。但是在复杂的物联网场景中，已知的后量子算法是否仍然可以有效运行并维护物联网安全，需要进一步探索。

（1）物联网环境加密需求

物联网安全最大的挑战在于：①物联网终端通常采用多种多样的嵌入式设备和轻量级处理器，相较于普通计算机，它们具有存储容量小、算力不足、数据存储时间长、更新难度大等特点，以及低成本、低功耗的需求；②物联网具有大规模、多协议、多种业务技术并存等特性，移动边缘计算的发展使得物联网面临众多异构终端用户接入，安全认证计算量大、通信安全性要求高[4]。

因此，新形势下物联网环境所采用的公钥加密体制必须满足以下需求。

1) 抗量子攻击：为了抵抗量子计算对传统加密算法的威胁，必须在物联网环境中采用后量子加密系统代替传统加密系统。

2) 轻量级架构：不同于普通互联网中的加密系统可以依靠大型服务器与高内存用户端进行密钥计算与存储，物联网终端设备往往数据容量小、计算力低、传输时延长，不适合采用过于复杂的加密体制。

3) 多参数方案：不同物联网环境对安全级别的要求不同，过高的安全级别对硬件的要求更高，提供多种参数选择可以针对不同的加密环境与硬件配置选择最适加密方案。

4) 模块化运算：在算法实施的各个环节中，尽量模块化处理，便于硬件调用。

5) 适配性良好：构造简洁，经过封装能够良好地应用于各种硬件电路，满足各种通信协议。

现有的用于物联网设备的加密算法中使用的大多是椭圆曲线加密算法。但是椭圆曲线加密算法不具备抗量子性，且其加密效率并不高。基于格的公钥加密算法的硬件实现在最近几年得到蓬勃发展，许多研究人员已经在嵌入式处理器上进行实验并报告了他们的实验结果。尤其是自2010年，环上容错学习（RLWE，ring-learning with error）问题被提出以来，密码学领域一直有科研人员尝试将基于RLWE问题的加密算法应用至硬件中。而在近5年中，伴随物联网的快速发展，对轻型物联网终端设备的RLWE加密应用更加成为研究热点，其中包括对现场可编程门阵列（FPGA，field programmable gate array）电路、Cortex-M系列微控制器、AVR-ATxmega系列单片机等小型硬件设备的加密应用与改进。

（2）基于格的公钥密码体制

基于格的公钥密码体制（lattice-based cryptography）是被研究最多的后量子加密体制之一。格是线性空间上确定的一组线性无关向量的整数线性组合。基于格的公钥加密体制根据不同的格上困难问题所构造，如最短向量问题（SVP，shortest vector problem）、最近向量问题（CVP，closest vector problem）、最短独立向量问题（SIVP，shortest independent vector problem）等。基于格的公钥密码体制通常将困难问题从平均情况难解性归约到可证明的最坏情况难解性，因此可以证明其具有很高的抗量子安全性。

基于格的公钥密码体制发展迅速，目前被认为具有前景的方案包括NTRU（n-th degree truncated polynomial ring units）加密、基于容错学习（LWE，learning with errors）困难问题的加密和基于RLWE困难问题的加密等。

本文的主要贡献如下。

2) 在改进的RBLWE算法中增加了加密安全性防护措施，从而能够抵御物联网环境中常见的侧信道攻击（具体包括时序攻击、简单功耗分析、差分功耗分析等），且加密效率依然很高。

1 相关工作

1.1 基于格的RLWE加密算法

Lyubashevsky等[5]2010年首次提出了RLWE问题，它是LWE问题在多项式环上进行改进后的表现形式。基于RLWE问题的加密算法被称为RLWE加密算法，它相较于LWE加密算法，具有密钥尺寸小、加密效率高等特性。

近年来，RLWE加密算法在基于格的后量子密码中愈发得到重视，其简洁的计算方式和小尺寸的密钥被认为在物联网环境下具有广阔的应用前景。

Pöppelmann等[6]首次将基于快速傅里叶变换（FFT，fast Flourier transform）的快速数论变换（NTT，number theoretic transform）算法应用在RLWE加密中的多项式乘法中，并通过实验验证NTT可以在硬件上得到很好的应用效果，提高了加密效率。此后，在不同轻量级设备上的RLWE加密研究越来越受到关注。

Roy等[7]、Fritzmann等[8]基于FPGA架构对RLWE加密中的NTT算法进行了进一步优化与仿真实验。Clercq等[9]使用了32位ARM的Cortex-M4F微处理器作为实验平台，并对高斯抽样算法和多项式乘法进行了优化，使得RLWE加密在软件上的应用速度提升了至少7倍。Boorghany等[10]首次在8 bit处理器上实现基于格的加密方案。Liu等[11]在8 bit AVR处理器上对NTT算法进行了改进，使用特殊的系数存储方法减少了多项式乘法的RAM占用空间。2020年，他们在ARM NEON和MSP430架构上首次实现了RLWE加密。Seo等[12]提出了一种基于8 bit AVR微控制器的安全紧凑的Ring-LWE加密方案，并给出了针对简单功耗分析和时序攻击的对策。

然而，对于物联网终端设备，尤其是一些需要长期运行并存储数据的小型设备而言，高斯分布和NTT算法的应用仍然被认为不够轻量。因此基于RLWE加密算法提出了BRLWE加密算法。

1.2 BRLWE加密

BRLWE加密算法最早由Buchmann等[13]于2016年在8 bit微型处理器ATXmega128和32 bit Cortex M0上进行了应用。不同于经典的RLWE加密算法，Buchmann等对和两个参数的选择均使用2的次幂，即在二进制中，模2相当于仅保留数值的低位，从而大大提高了模运算的效率。

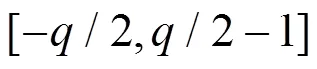
此外，Xie等[18]提出了一种novel LUT-like的多项式乘法方案。他们利用4输入乘法器作为多项式乘法的最小计算单元，在每次进行多项式乘法时，将项系数两两拆分，再通过乘法器进行分别运算。He等[19]对多项式乘法从硬件角度进行了解构，在硬件配置上做了相关改进。上述研究成果选取了一些新颖的角度进行研究，也十分具有启发性。

BRLWE算法的多项式运算模块的改进与安全性保障是将BRLWE真正应用于物联网终端的研究重点。

2 算法改进

2.1 符号说明

为更好地理解本文加密算法的实现过程，对本文常用符号进行如下约定和说明。

2.2 算法介绍

本文提出了Sym-BRLWE（symmetrical binary RLWE）算法，该算法改进了BRLWE加密，具体为调整了离散均匀分布上的随机数选取，优化了多项式乘法的计算细节。

1) 数据量更小，计算更便捷，能够更好地在轻量级设备上快速运算；

2) 省去了离散高斯分布抽样过程，加快了运算时间；

算法1 BRLWE加密算法

密钥生成

加密

解密

BRLWE解密正确性分析如下：

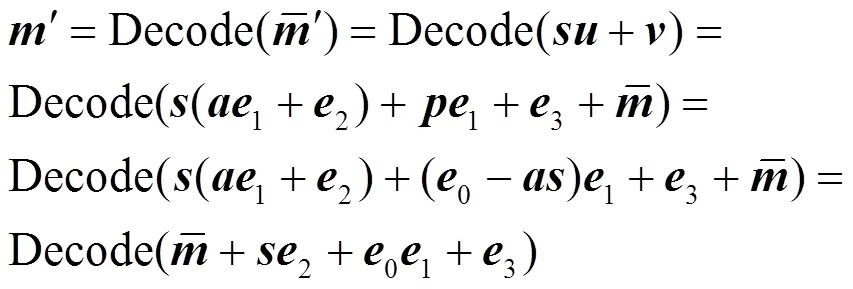
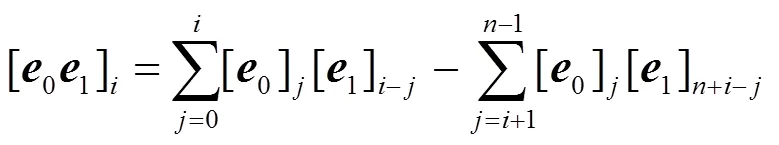
则其均值为：

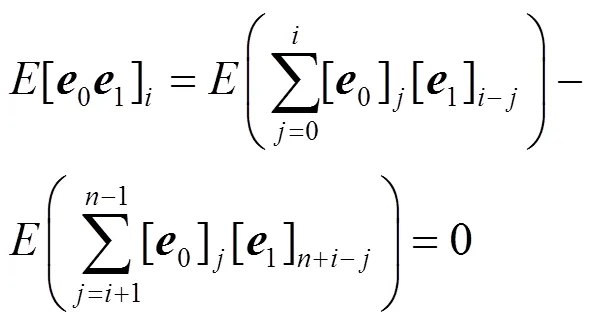
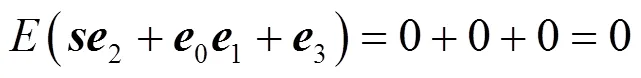
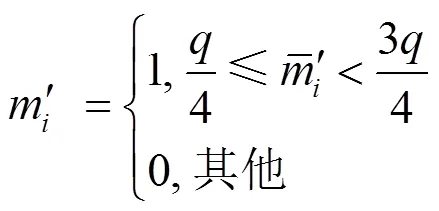
2.3 物联网环境下算法的实现

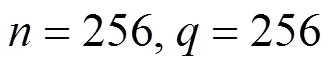
（1）随机数生成

（2）环上多项式运算

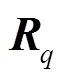
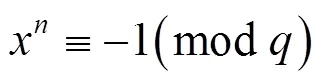
环上多项式加法计算如算法2、算法3所示。

算法2 环上多项式加法计算（含二进制多项式）

算法3 环上多项式加法计算（不含二进制多项式）

多项式乘法计算如算法4所示，本算法在文献[15]中所述的循环移位方法的基础上，简化了多项乘法计算步骤。

算法4 环上多项式乘法计算

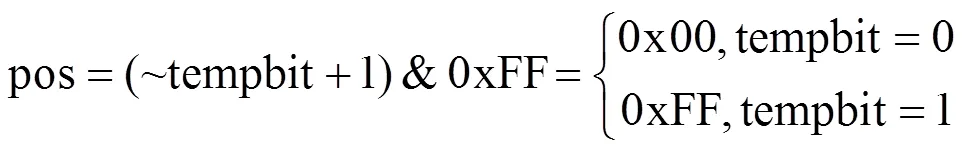
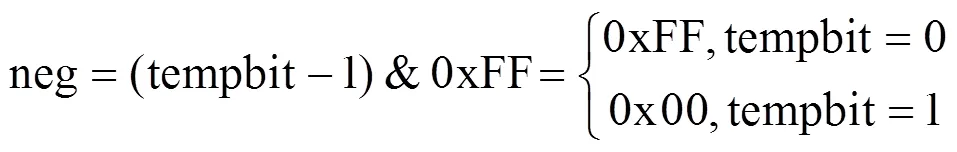
表1 Sym-BRLWE加密时间

表2 Sym-BRLWE各数据存储空间

3 安全性分析

3.1 格攻击

对于基于格的后量子加密算法而言，存在许多根据格困难问题本身进行的攻击，称之为格攻击。常见的格攻击方法主要是一些格基约减算法如LLL（Lenstra–Lenstra–Lovász）、BKZ（Block Korkine- Zolotarev）等，它们通过将格基进行约减变化使格上困难问题的求解变得容易。BRLWE算法基于的BRLWE问题是RLWE问题的变体。文献[21]简单地证明了BRLWE问题至少与标准LWE问题一样困难，因此本文认为BRLWE问题基于的格上数学难题是足够难解的，算法理论是足够安全的。

3.2 侧信道攻击

侧信道攻击（SCA，side channel attack）是一种对加密硬件的攻击方式，包括时序攻击、能量分析、错误注入等方式。不同于针对算法本身的软件攻击，它通过对加密时的信道进行监测，对各硬件计算和传输数据时泄露的信息进行攻击，而无须侵入算法内部。下面将从侧信道攻击的角度对Sym-BRLWE进行安全分析。

（1）时序攻击

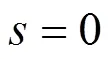
（2）SPA攻击

SPA攻击对硬件电流随时间变化的情况进行监测与分析，电子元件在执行不同操作时，功耗会发生变化[22]。

在原始的BRLWE加密中，当二进制多项式系数遇“0”时不进行任何计算，只有在遇“1”时才进行加法运算，这将给SPA攻击提供可乘之机。例如，在解密过程中，SPA攻击能够判断是否进行了加法运算产生的功耗差异，从而破解私钥。而在Sym-BRLWE中，由于将“0”实际上视作“−1”，无论二进制多项式的系数是“0”还是“1”，都要进行加法和减法以及与运算，运算相同则功耗也相同，因此该算法可以抵抗SPA攻击。

（3）DPA攻击

SPA攻击只在分析单个运算操作下有效，而对于同时进行多个操作的系统，由于信号的混合，SPA将无能为力。DPA则将有加密操作的信号减去没有加密操作的噪声从而得到需要分析的关键信号。只要获取足够多的能量迹线并进行统计分析，DPA攻击就能够发掘细微的功耗与密钥之间的联系，因此DPA更难预防[23]。

（4）FI攻击

FI攻击能够针对系统中的数据或控制单元进行攻击。攻击者将错误信息注入内存或信号以利用函数的错误执行从而提取秘密数据（如未加密的明文或私钥等）。

文献[17]中提到的应对FI攻击的措施同样可以应用到本文方案中，关于错误注入攻击的防御将在未来进行进一步研究。

4 实验分析

本节对文献[13]、[14]和[16]中提出的基于BRLWE加密算法和本文提出的Sym-BRLWE加密算法进行实验仿真与比较。算法代码基于Python语言编写，仿真环境为64 bit Windows10专业版，Python 3.7.2，硬件配置为Intel(R) Core(TM) i5-7200U 2.50 GHz 2.70 GHz CPU处理器及8 GB RAM。本仿真实验对各算法分别根据的取值选择两种参数方案，如表3所示，然后对512 bit的二进制明文加密，进行200次实验取均值，并根据结果比较包括密钥生成时间、加密时间、解密时间、私钥大小、公钥大小、密文大小等加密特征。

经过仿真后得到的各加密算法的时间消耗和数据大小统计分别如表4、表5所示。

表3 RBLWE加密参数及对应安全级别

注：安全级别中的“/”前后数字表示表示传统安全级别和量子安全级别。

表4 各加密算法时间消耗统计

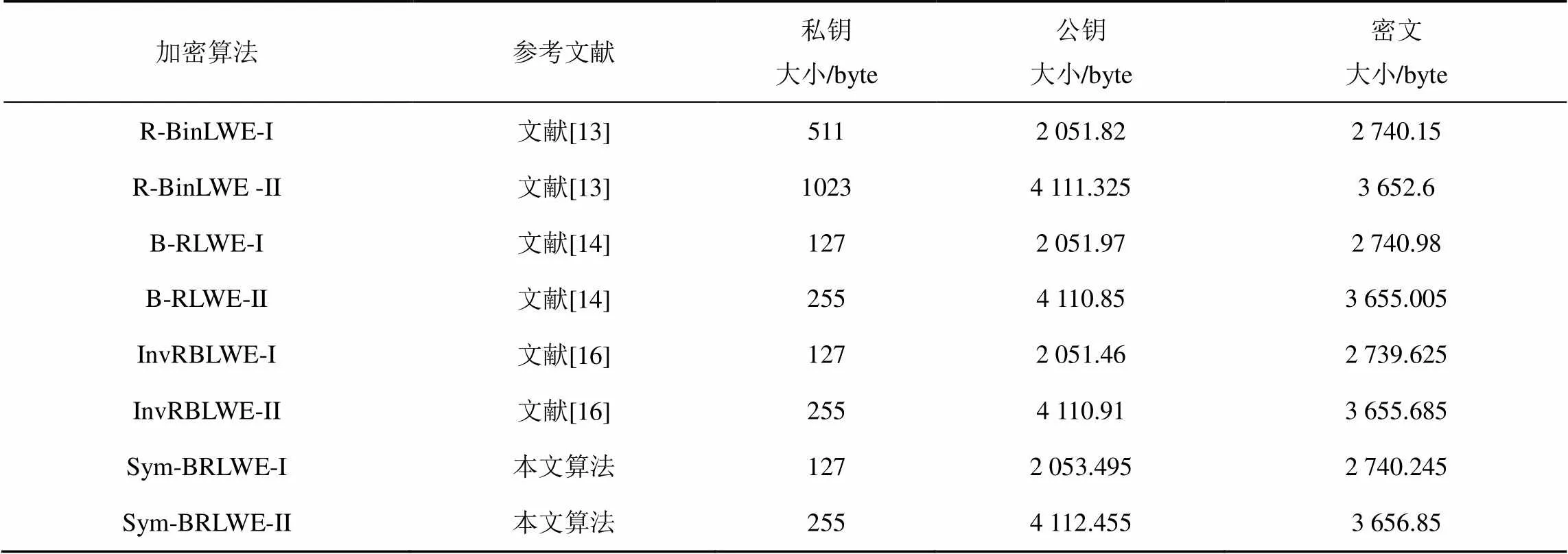
表5 各加密算法数据大小统计

从表4能够看出，在各算法中，更高的安全级别必然需要更大的时间消耗。而比较同一安全级别下的各个加密算法，可以看出R-BinLWE在各阶段所需时间均为最短，这是因为R-BinLWE仅仅基于原始的BRLWE构造，没有任何安全性措施，缺乏抵抗侧信道攻击的能力。R-BinLWE是最原始的理想化算法，安全性很弱，仅作为其他算法的比较参考。InvRBLWE所需时间在4种加密算法中相对最长，这是因为InvRBLWE为抵抗SPA、DPA攻击在加密过程中采用了掩码操作，做出了一定的效率牺牲。它的安全性能够保证，但效率低于Sym-BRLWE。此外，Sym-BRLWE相较于B-RLWE也有一定效率优势。B-RLWE的时间消耗主要源于其在抵御DPA攻击时增加了一次环上随机数生成环节。

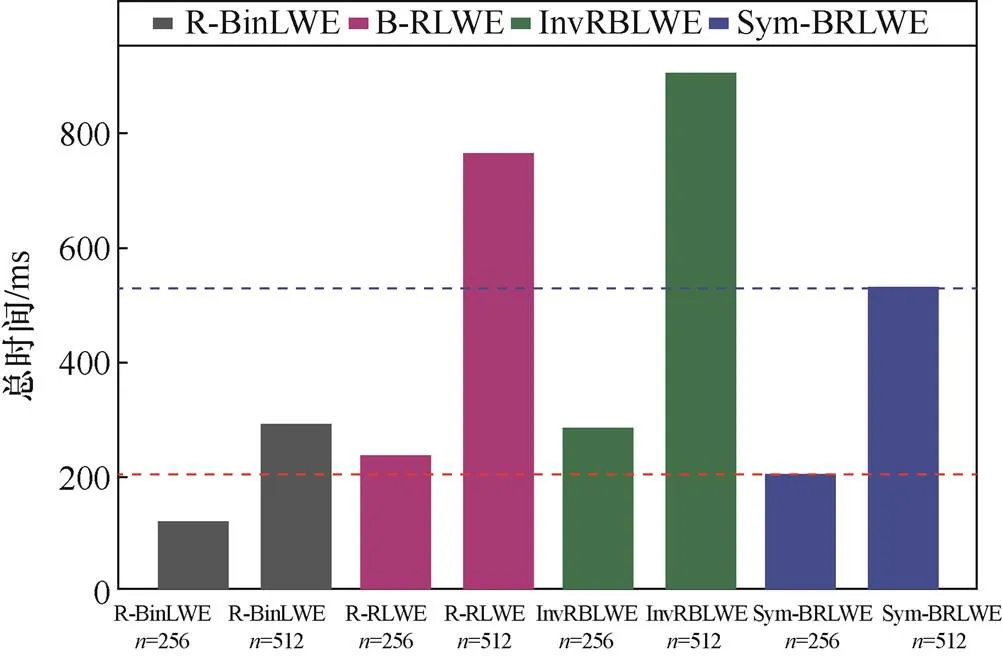
图1 各算法加解密总时间比较

Figure 1 Comparison of the total encryption time of each algorithm

Sym-BRLWE的效率优势在根本上主要体现在：多项式乘法上减去了一个判断分支；解密时不需要额外的解码运算；省去了一些耗时的安全性措施。因此Sym-BRLWE在安全性不弱于其他上述算法的情况下，效率上具有明显的优势。

从表5给出的加密算法数据大小统计中可以看到，Sym-BRLWE保证了与B-RLWE和InvRBLWE的一致，即私钥大小比原始R-BinLWE方案要小75%，而公钥大小、密文大小与原始方案不变。由于R-BinLWE在生成二进制多项式时，没有使用8 bit二进制随机数生成器生成数字再进行按位截取，因此占用了大量冗余空间。其他3个算法均针对轻量硬件设备考虑到这一点，因此私钥大小得到了大幅缩小。

5 结束语

本文提出了一种后量子加密算法Sym-BRLWE，该算法具有更高的加密效率，更小的密钥尺寸，同时能够抵御时序攻击、SPA、DPA等侧信道攻击，因此更加适用于物联网应用。经过仿真实验验证，在8 bit运算背景选择140 bit的量子安全级别参数时，相较于其他已有BRLWE算法，加密总时间能够减少至少30%，证明了Sym-BRLWE加密算法比其他已提出的BRLWE相关算法加密效率更高。本文的研究存在一些尚未解决的问题有待后续的进一步拓展研究，包括仿真实验可以拓展到更真实的硬件环境中进行，探讨更适宜于新型物联网硬件框架的优化机制与方法等。

[1] SCHNEIER B. IoT cybersecurity: what's plan B[R]. 2017.

[2] 朱小伶. 2020年量子计算技术发展综述[J]. 无人系统技术, 2021, 4(2): 26-32.

ZHU X L. Survey of quantum computing technology in 2020[J]. Unmanned Systems Technology, 2021, 4(2): 26-32.

[3] 张成磊, 付玉龙, 李晖, 等. 6G网络安全场景分析及安全模型研究[J]. 网络与信息安全学报, 2021, 7(1): 28-45.

ZHANG C L, FU Y L, LI H, et al. Research on security scenarios and security models for 6G networking[J]. Chinese Journal of Network and Information Security, 2021, 7(1): 28-45.

[4] 陈璐, 汤红波, 游伟, 等. 移动边缘计算安全防御研究[J]. 网络与信息安全学报, 2021, 7(1): 130-142.

CHEN L, TANG H B, YOU W, et al. Research on security defense of mobile edge computing[J]. Chinese Journal of Network and Information Security, 2021, 7(1): 130-142.

[5] LYUBASHEVSKY V, PEIKERT C, REGEV O. On ideal lattices and learning with errors over rings[M]//Advances in Cryptology – EUROCRYPT 2010. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 1-23.

[6] PÖPPELMANN T, GÜNEYSU T. Towards efficient arithmetic for lattice-based cryptography on reconfigurable hardware[M]//Progress in Cryptology-LATINCRYPT 2012. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 139-158.

[7] ROY S S, VERCAUTEREN F, MENTENS N, et al. Compact ring-LWE cryptoprocessor[C]//Cryptographic Hardware and Embedded Systems – CHES 2014. 2014: 371-391.

[8] FRITZMANN T, SEPÚLVEDA J. Efficient and flexible low-power NTT for lattice-based cryptography[C]//Proceedings of 2019 IEEE International Symposium on Hardware Oriented Security and Trust. 2019: 141-150.

[9] DE CLERCQ R, ROY S S, VERCAUTEREN F, et al. Efficient software implementation of ring-LWE encryption[C]//Proceedings of Design, Automation & Test in Europe Conference & Exhibition (DATE). 2015: 339-344.

[10] BOORGHANY A, SARMADI S B, JALILI R. On constrained implementation of lattice-based cryptographic primitives and schemes on smart cards[J]. ACM Transactions on Embedded Computing Systems, 2015, 14(3): 1-25.

[11] LIU Z, AZARDERAKHSH R, KIM H, et al. Efficient software implementation of ring-LWE encryption on IoT processors[J]. IEEE Transactions on Computers, 2020, 69(10): 1424-1433.

[12] SEO H, KWON H, KWON Y, et al. Fast number theoretic transform for ring-LWE on 8-bit AVR embedded processor[J]. Sensors, 2020, 20(7): 2039.

[13] BUCHMANN J, GÖPFERT F, GÜNEYSU T, et al. High- performance and lightweight lattice-based public-key encryption[C]//Pro- ceedings of the 2nd ACM International Workshop on IoT Privacy, Trust, and Security. 2016: 2-9.

[14] AYSU A, ORSHANSKY M, TIWARI M. Binary Ring-LWE hardware with power side-channel countermeasures[C]//Proceedings of 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE). 2018: 1253-1258.

[15] EBRAHIMI S, BAYAT-SARMADI S, MOSANAEI-BOORANI H. Post-quantum cryptoprocessors optimized for edge and resource-constrained devices in IoT[J]. IEEE Internet of Things Journal, 2019, 6(3): 5500-5507.

[16] EBRAHIMI S, BAYAT-SARMADI S. Lightweight and DPA-resistant post-quantum cryptoprocessor based on binary ring-LWE[C]//Proceedings of 2020 20th International Symposium on Computer Architecture and Digital Systems (CADS). 2020: 1-6.

[17] EBRAHIMI S, BAYAT-SARMADI S. Lightweight and fault-resilient implementations of binary ring-LWE for IoT devices[J]. IEEE Internet of Things Journal, 2020, 7(8): 6970-6978.

[18] XIE J F, HE P Z, WEN W J. Efficient implementation of finite field arithmetic for binary ring-LWE post-quantum cryptography through a novel lookup-table-like method[C]//Proceedings of 2021 58th ACM/IEEE Design Automation Conference. 2021: 1279-1284.

[19] HE P Z, GUIN U, XIE J F. Novel low-complexity polynomial multiplication over hybrid fields for efficient implementation of binary ring-LWE post-quantum cryptography[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2021, 11(2): 383-394.

[20] FERNÁNDEZ-CARAMÉS T M. From pre-quantum to post-quantum IoT security: a survey on quantum-resistant cryptosystems for the Internet of Things[J]. IEEE Internet of Things Journal, 2020, 7(7): 6457-6480.

[21] BUCHMANN J, GÖPFERT F, PLAYER R, et al. On the hardness of LWE with binary error: Revisiting the hybrid lattice-reduction and meet-in-the-middle attack[C]//International Conference on Cryptology in Africa. 2016: 24-43.

[22] PARK A, HAN D G. Chosen ciphertext simple power analysis on software 8-bit implementation of ring-LWE encryption[C]//Pro- ceedings of 2016 IEEE Asian Hardware-Oriented Security and Trust (AsianHOST). 2016: 1-6.

[23] KOCHER P, JAFFE J, JUN B, et al. Introduction to differential power analysis[J]. Journal of Cryptographic Engineering, 2011, 1(1): 5-27.

Post-quantum encryption technology based on BRLWE for internet of things

GAO Yitian, CHEN Liquan, TU Tianyang,GAO Yuan, CHEN Qianye

School of Cyber Science and Engineering, Southeast University, Nanjing 210096, China

With the development of quantum computers, the classical public key encryption system is not capable enough to guarantee the communication security of internet of things (IoT). Because the mathematical puzzles which post-quantum encryption algorithms are based on cannot yet be broken by quantum computers, these new algorithms have good anti-quantum computing security. In particular, the lattice-based cryptography is expected to become the main technology of the next generation public key cryptosystem. However, post-quantum encryption algorithms have the disadvantages of large amount of computation and high storage space. The communication efficiency of IoT will be affected if post-quantum encryption algorithms are directly applied to the lightweight device under IoT environment. In order to better guaranteethe communication security and improve the commutation efficiency of IoT, Sym-BRLWE (symmetrical binary RLWE) encryption scheme was proposed. Sym-BRLWE was improved from the existing post-quantum encryption scheme based on BRLWE (binary ring- learning with errors) problem. Specifically, Sym-BRLWE encryption algorithm met the efficiency requirements of IoT via improving the random number selection on the discrete uniform distribution and the calculation of the polynomial multiplication. Sym-BRLWE encryption algorithm achieved high efficiency and high security via adding encryption security precautions, thenit ismore suitable for IoT lightweight devices. From the security analysis, the proposed Sym-BRLWE encryption scheme had high security. It could theoretically resist lattice attacks, timing attacks, simple power analysis (SPA) and differential power analysis (DPA). From simulation experiments, which were carried out in a binary computing environment simulating an 8-bit micro-device, the proposed Sym-BRLWE encryption scheme has high efficiency and small key size in encryption and decryption. It could reduce the total encryption time by 30% to 40% when compared with other BRLWE-based encryption schemes with the parameter selection of the 140bit quantum security level.

post-quantum cryptography, internet of things, public key encryption, lattice-based encryption system, ring-learning with errors

TP393

A

10.11959/j.issn.2096−109x.2022024

2021−08−31；

2021−10−15

陈立全，Lqchen@seu.edu.cn

国家重点研发计划（2020YFE0200600）

TheNational Key R&D Program of China（2020YFE0200600）

高艺恬, 陈立全, 屠天扬, 等. 基于BRLWE的物联网后量子加密技术研究[J]. 网络与信息安全学报, 2022, 8(5): 140-149.

Format: GAO Y T, CHEN L Q, TU T Y, et al. Post-quantum encryption technology based on BRLWE for internet of things[J]. Chinese Journal of Network and Information Security, 2022, 8(5): 140-149.

高艺恬（1998−），女，江苏南京人，东南大学硕士生，主要研究方向为后量子密码、物联网安全。

陈立全（1976−），男，广西玉林人，东南大学教授、博士生导师，主要研究方向为物联网安全、密码协议等。

屠天扬（1997−），女，浙江嘉兴人，东南大学硕士生，主要研究方向为后量子密码、物联网安全。

高原（1994−），女，山东烟台人，东南大学博士生，主要研究方向为云数据去重、物联网数据安全。

陈芊叶（1997−），女，江苏扬州人，东南大学硕士生，主要研究方向为物联网安全、量子密钥分发。