基于SAT方法进一步加速差分特征的搜索

许峥

基于SAT方法进一步加速差分特征的搜索

许峥1,2

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2. 中国科学院大学网络空间安全学院，北京 100049）

差分分析；差分特征；自动化搜索；SAT求解器

0 引言

20世纪90年代初，Biham和Shamir提出了差分分析[1]。差分分析最初是一种用于评估DES分组密码安全性的密码分析方法，后来被用于评估各种分组密码的安全性。对于对称密码原语的密码分析，差分分析是评估对称密码原语安全性的最强技术之一。此外，抗差分分析是现代分组密码算法的主要设计标准。

对于差分分析，一个关键的步骤是找到高概率的差分特征。目前，使用自动化方法搜索差分特征已成为一种新趋势。在1994年欧密会议上[2]，Matsui提出了一种分支定界算法来自动化搜索基于S盒的分组密码的最优差分特征。后来，Matsui的算法被用于自动化搜索ARX密码的差分特征[3-6]。

21世纪初期，自动化工具由于在搜索分组密码的差分特征方面表现出优越的性能而备受关注。最重要的自动化工具之一是基于混合整数线性规划（MILP）的方法。Mouha等[7]首次引入了该方法，并用其评估了差分、线性活跃S盒数量的下界。后来，上述方法被改进并应用于搜索面向比特的分组密码的（相关密钥）差分特征。此外，MILP方法被进一步应用于搜索各种类型的区分器[8-11]。

另一种备受关注的自动化工具是基于布尔可满足性问题（SAT）的方法。2013年，Mouha等[12]首次引入了该方法，并将其用于搜索Salsa20的3轮最优差分特征。后来，在2015年美密会议上，Kölbl等[13]使用上述方法搜索SIMON的最优差分和线性特征。此外，SAT方法被进一步应用于搜索各种类型的区分器[14-18]。

为了使用上述自动化工具搜索差分特征，密码分析者只需要将差分传播转化为相应的不等式或约束条件，这极大地简化了密码分析者的工作，并最大限度地减少了人为错误的可能性。然而，上述两种自动化工具在搜索阶段的执行效率取决于第三方求解器的性能、差分性质的等式/不等式的表示方式以及一些优化策略。

为了提高MILP方法的效率，密码分析者提出了多种优化策略。2017年，Sasaki和Todo[19]对于描述S盒的差分传播提出了一种确保不等式数量最少的方法。在2018年ISC会议上，Zhang等[20]通过将Matsui边界条件加入MILP模型中来加速差分特征的搜索。2019年，Zhou等[21]利用差分特征概率与活跃S盒数量之间的关系优化差分特征的搜索。2020年，Boura和Coggia[22]对于SPN结构的S盒以及线性层提出了高效的MILP模型，以提高搜索效率。

然而，与MILP方法效率的提高相比，使用SAT方法对自动化搜索加速的研究相对滞后。2016 年，Song等[23]提出了一种启发式的方法搜索ARX密码更好的差分特征。2021年，Sun等[24]通过将Matsui边界条件加入SAT方法中来加速差分特征的搜索。

当密码分析者利用SAT方法搜索分组密码的最优差分特征时，他们经常使用STP[25]以及CryptoMiniSat[26]。由于CryptoMiniSat支持多线程且STP支持多种询问条件，本文提出以下两个问题。①使用多线程是否可以加速搜索？②使用不同的询问条件是否会影响搜索的耗时？因此，研究线程数和询问条件的加速效果是十分重要的。

本文改进了文献[24]中的方法，并且研究了线程数和询问条件的加速效果，主要贡献有以下3方面。

（1）改进的边界条件

在文献[24]中，Sun等将Matsui边界条件转化为合取范式（CNF）的形式并将其加入SAT方法中来加速差分特征的搜索。由于搜索空间可以被进一步减小，他们的方法可以被优化。为了进一步提高搜索效率，本文改进了Matsui边界条件并提出了一种改进的方法搜索分组密码的最优差分特征。

（2）选择线程数以及询问条件的策略

为了研究线程数和询问条件的加速效果，本文使用STP和CryptoMiniSat分别搜索SPECK96和HIGHT的差分特征，并比较了在不同线程数和询问条件下求解SAT/SMT问题的耗时。本文的实验结果表明，线程数对搜索差分特征的耗时影响较大，而询问条件对搜索差分特征的耗时影响较小。从而，本文提出了一种如何选择线程数和询问条件的策略，并发现STP会影响搜索的整体效率。

（3）自动化搜索HIGHT的11轮最优差分特征

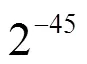
1 符号、预备知识及算法简介

1.1 符号

本文使用的符号及含义如表1所示。

表1 符号及含义

1.2 预备知识

定义2 模加的异或差分概率[27]

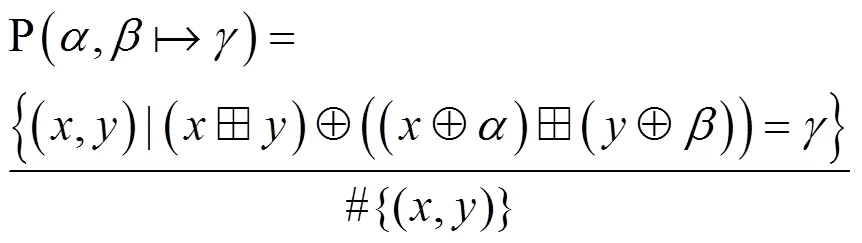
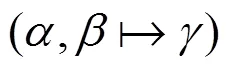
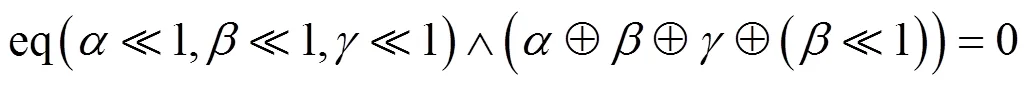
其中

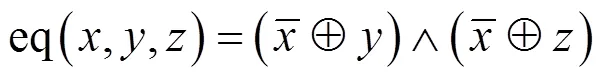
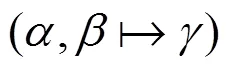
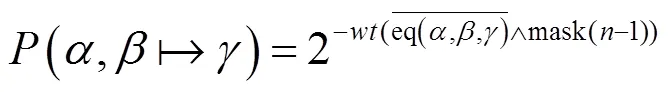
1.3 SPECK简介

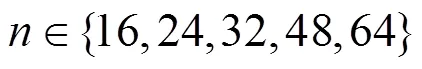
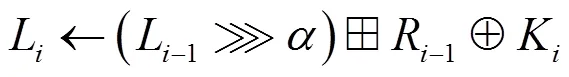
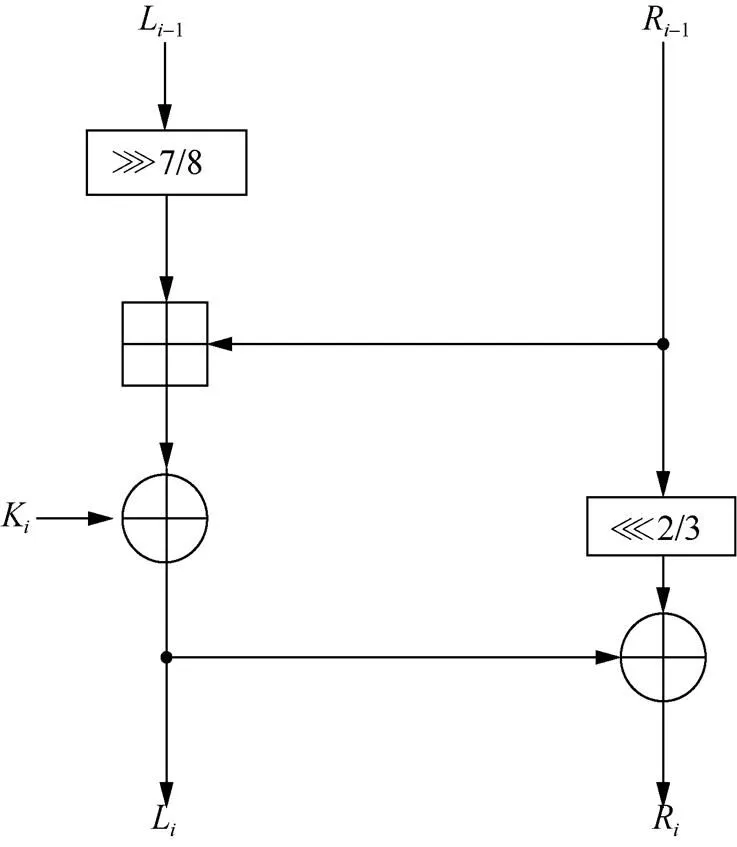
图1 SPECK轮函数

Figure 1 The round function of SPECK

1.4 HIGHT简介

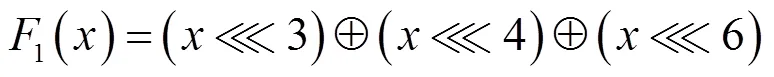
2 改进Matsui边界条件

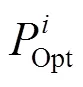
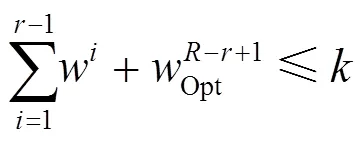
其中，表示（即轮最优差分特征中第i轮差分特征的概率）的以2为底数的对数的绝对值。下文将式(7)称为边界条件。

Figure 2 The round function of HIGHT

2.1 改进边界条件

算法1 Sun等方法的搜索过程

4) end for

8) end for

9) 将边界条件以及L-M条件转化为CNF形式;

11) 调用SAT求解器CaDiCaL来确定是否存在轮最优差分特征;

12) if存在轮最优差分特征then

14) end if

15) if不存在轮最优差分特征then

17) end if

18) end while

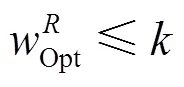
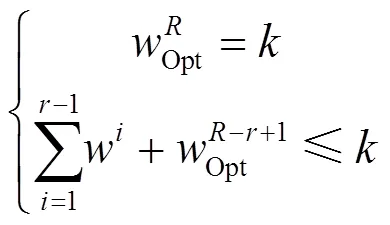
算法2 改进后的带改进的边界条件的搜索过程

4) end for

9) end for

10) 将改进的边界条件以及L-M条件转化为CNF形式;

12) 调用SAT求解器来确定是否存在轮最优差分特征;

13) if存在轮最优差分特征then

15) end if

16) if不存在轮最优差分特征then

18) end if

19) end while

3 线程数和询问条件的加速效果

当密码分析者利用SAT方法搜索分组密码的最优差分特征时，密码分析者需要将搜索差分特征的问题转化为布尔可满足性问题（即SAT问题）。然而，SAT问题仅包含布尔变量以及布尔操作（AND、NOT以及OR），因此上述转化过程十分复杂。相比之下，可满足性模理论（即SMT）问题支持比特向量变量以及常用的比特向量操作。此外，SMT问题是SAT问题的推广且SMT公式可以用更丰富的逻辑表达。因此，密码分析者通常将搜索差分特征的问题转化为SMT问题，并使用SMT求解器进行求解，过程如下。

1) 将搜索差分特征的问题转化为SMT问题。

2) 利用SMT求解器将SMT问题转化为SAT问题。

3) 利用SMT求解器调用SAT求解器求解SAT问题。

STP[25]是一种典型的SMT求解器，本文利用STP求解所有的SMT问题。

3.1 线程数的加速效果

STP的默认SAT求解器是MiniSAT[30]。然而，STP同样支持其他的SAT求解器，如CryptoMiniSat[26]。由于CryptoMiniSat支持多线程且支持异或操作以及高斯消元，密码学者经常利用CryptoMiniSat作为后端SAT求解器来求解SAT问题。因此，使用多线程是否可以加速搜索成为一个很自然的问题。

为了研究线程数的加速效果，本文使用STP和CryptoMiniSat分别搜索SPECK96和HIGHT的差分特征。

3.2 询问条件的加速效果

为了将搜索差分特征的问题转化为SMT问题，密码分析者经常使用CVC语言描述异或差分传播。当搜索差分特征时，一个常用的搜索策略是询问在当前概率约束下是否存在有效的差分特征。上述策略所对应的询问条件为QUERY (FALSE)，COUNTEREXAMPLE。

上述询问条件被称为错误询问。当STP返回Invalid以及一条差分特征时，代表在当前概率约束下至少有一条有效差分特征。

直观上看，使用上述搜索策略是很耗时的，尤其是在当前概率约束下没有有效差分特征时。因此，替换询问条件是否可以加速搜索成为一个很自然的问题。

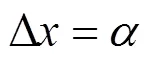
3.3 线程数和询问条件加速效果的实验测试

3.3.1 追踪差分传播

（1）追踪SPECK96中的差分传播

利用如下约束条件追踪SPECK96中的差分转播。

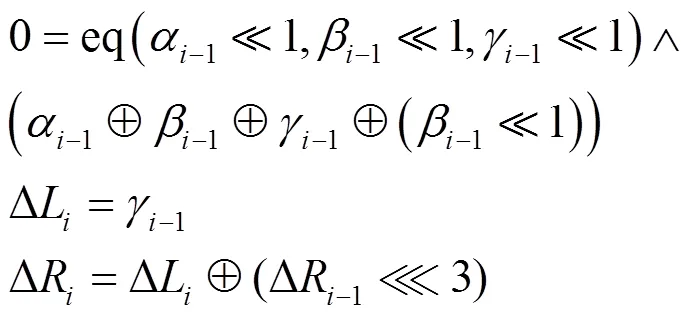
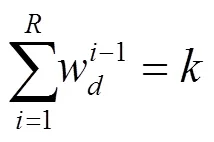
（2）追踪HIGHT中的差分传播

利用如下约束条件追踪HIGHT中的差分转播。

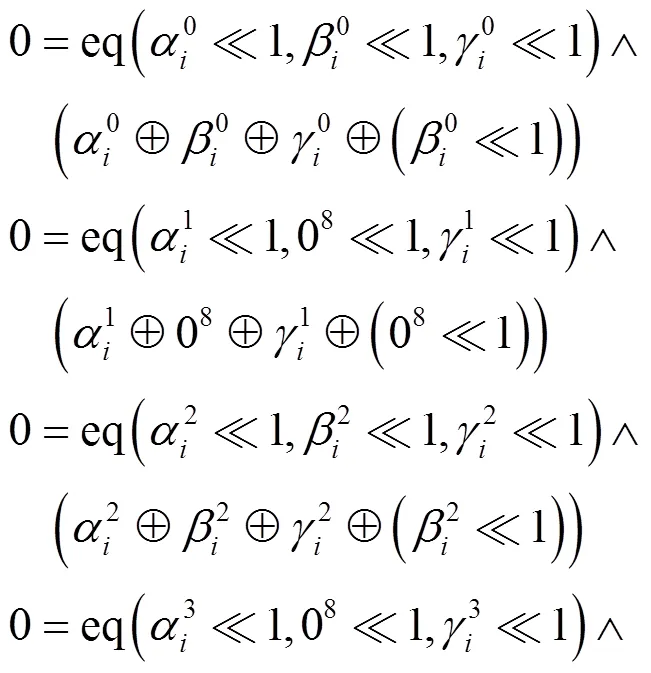
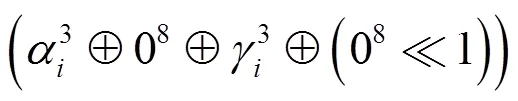
其中，

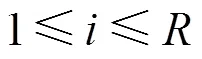
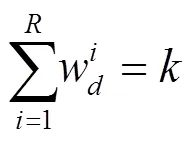
3.3.2 线程数和询问条件加速效果的实验测试

本节分别利用1～30个线程搜索SPECK96以及HIGHT的差分特征并记录耗时，从而实验测试线程数的加速效果。此外，分别利用错误询问以及输入询问搜索SPECK96以及HIGHT的差分特征并记录耗时，从而实验测试询问条件的加速效果。

3.3.2.1 搜索SPECK96的差分特征

令=8且=24，测试线程数以及询问条件的加速效果（以单线程+错误询问为基准）。

（1）线程数的加速效果

①当询问条件是错误询问时

时间消耗随着线程数增加的变化趋势是：先减少，再增多，最后减少并趋于平稳。两个转折点分别是4线程以及11线程。

②当询问条件是输入询问时

时间消耗随着线程数增加的变化趋势是：先减少，再增多并趋于平稳，最后减少并趋于平稳。两个转折点分别是5线程以及13线程。

（2）询问条件的加速效果

当线程数不为5或者8时，利用错误询问搜索差分特征的耗时与利用输入询问搜索差分特征的耗时之间没有明显的差距。实验结果如图3所示。

令=8且=25，测试线程数以及询问条件的加速效果（以单线程+错误询问为基准）。

（1）线程数的加速效果

①当询问条件是错误询问时

当线程数不超过11时，时间消耗随线程数增加没有明显变化的规律：时间消耗从减少到增多的转折点分别为2、4、6和10线程；时间消耗从增多到减少的转折点分别为3、5和8线程。当线程数超过11且不超过20时，时间消耗随着线程数的增加而减少。当线程数超过20且不超过30时（除了26），时间消耗随着线程数的增加几乎不变。当线程数为26时，时间消耗最少。

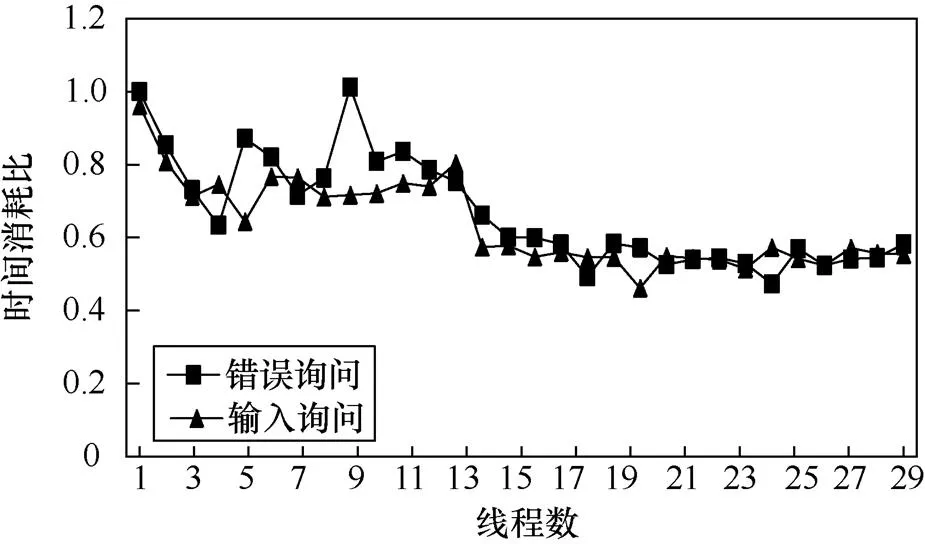
图3 搜索SPECK96的概率为2−24的8轮差分特征的时间消耗比

Figure 3 The time consumption ratio of searching for 8-round differential characteristics with a probability of 2−24of SPECK96

②当询问条件是输入询问时

当线程数不超过13时，时间消耗随线程数增加没有明显变化的规律：时间消耗从减少到增多的转折点分别为2、6、9和12线程；时间消耗从增多到减少的转折点分别为4、7和11线程。当线程数超过13且不超过19时，时间消耗随着线程数的增加先减少后增多，且转折点为18线程。当线程数超过19且不超过30时，时间消耗随着线程数的增加几乎不变。

（2）询问条件的加速效果

尽管在大多数情况下，利用错误询问搜索差分特征的耗时少于利用输入询问搜索差分特征的耗时，然而，耗时之间的差距并不十分明显。实验结果如图4所示。

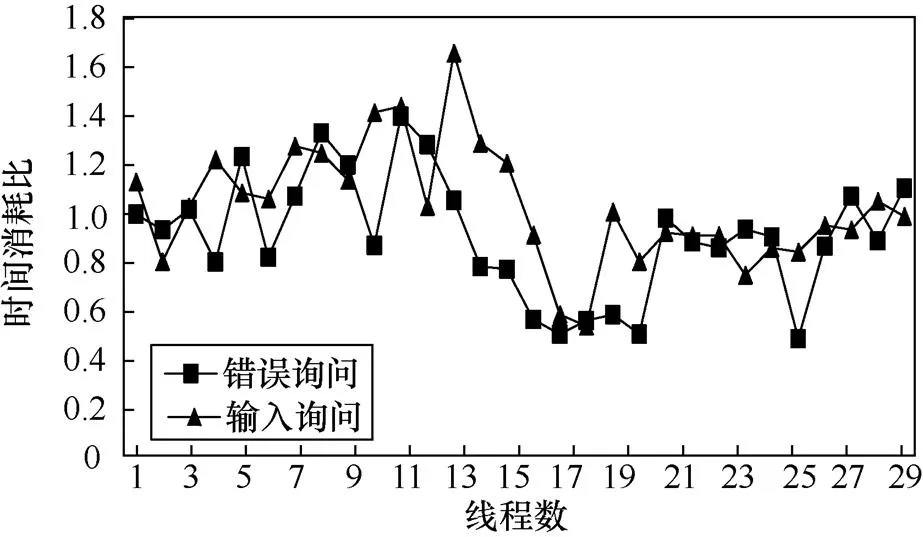
图4 搜索SPECK96的概率为2−25的8轮差分特征的时间消耗比

Figure 4 The time consumption ratio of searching for 8-round differential characteristics with a probability of 2−25of SPECK96

令=8且=26，测试线程数以及询问条件的加速效果（以单线程+错误询问为基准）。

（1）线程数的加速效果

①当询问条件是错误询问时

时间消耗随着线程数增加的变化趋势分为5个阶段（减少→增多→减少→增多→减少并趋于平稳）。4个转折点分别是2、7、10以及13线程。

②当询问条件是输入询问时

当线程数不超过6时，时间消耗随线程数增加没有明显变化的规律：时间消耗从减少到增多的转折点分别为3线程和5线程；时间消耗从增多到减少的转折点为4线程。当线程数超过6时，时间消耗随着线程数增加的变化趋势是：先减少并趋于平稳，后增多。转折点为25线程。

（2）询问条件的加速效果

尽管在大多数情况下，利用错误询问搜索差分特征的耗时少于利用输入询问搜索差分特征的耗时，然而，耗时之间的差距并不十分明显。实验结果如图5所示。

图5 搜索SPECK96的概率为2−26的8轮差分特征的时间消耗比

Figure 5 The time consumption ratio of searching for 8-round differential characteristics with a probability of 2−26of SPECK96

3.3.2.2 搜索HIGHT的差分特征

令=11且=39，测试线程数以及询问条件的加速效果（以单线程+错误询问为基准）。

（1）线程数的加速效果

①当询问条件是错误询问时

时间消耗随着线程数增加的变化趋势是：先减少并趋于平稳，再增多，最后减少并趋于平稳。两个转折点分别是11线程以及12线程。

②当询问条件是输入询问时

时间消耗随着线程数增加的变化趋势分为5个阶段（减少→增多→减少并趋于平稳→增多→减少并趋于平稳）。4个转折点分别是2、3、9以及11线程。

（2）询问条件的加速效果

图6 搜索HIGHT的概率为2−39的11轮差分特征的时间消耗比

Figure 6 The time consumption ratio of searching for 11-round differential characteristics with a probability of 2−39of HIGHT

根据实验结果发现，线程数对搜索差分特征的耗时影响较大，而询问条件对搜索差分特征的耗时影响较小。对于相同的分组密码，尽管时间消耗随着线程数增加变化的总体趋势是减少的，但“使用较多线程数导致较高耗时”的情况并不罕见，因此，盲目地选择较多的线程数可能会导致更低的搜索效率。并且，对于不同的分组密码，线程数的加速效果是不同的。此外，利用两个线程搜索差分特征的耗时基本低于利用单线程搜索差分特征的耗时。因此，对于某个特定的分组密码，如果密码分析者在搜索差分特征之前没有实验测试线程数的加速效果（如同本文所做的实验），利用两个线程搜索差分特征将是一个较好的选择。

对于上述4组实验，有对应的4组SMT问题。需要注意的是，每组SMT问题中的两个SMT问题仅询问条件不同。利用STP将这8个SMT问题转化为对应的8个SAT问题。然而，每组SAT问题中的两个SAT问题是完全相同的。这就意味着，仅改变询问条件将不会影响CryptoMiniSat的求解效率。因此，利用错误询问搜索差分特征的耗时与利用输入询问搜索差分特征的耗时之间的差距是STP引起的。这意味着STP会影响搜索的整体效率。

在上述实验中，时间消耗随着线程数的增加先减少后增加的情况多次出现。然而，上述现象出现的线程数位置以及范围均无明显规律，可能与以下两个原因有关：线程增加导致线程调度时间开销增加；第三方求解器的内部优化逻辑不够完善。此外，线程数增加到一定数量时，时间消耗趋于平缓而无法进一步降低，可能与以下原因有关：采用多线程进行搜索时，多个线程要操作同一个数据集合，线程状态将频繁改变，导致在线程数达到某个阈值时，线程数的增加无法进一步提高程序的性能。

4 自动化搜索HIGHT的11轮最优差分特征

表2 HIGHT的11轮最优差分特征

5 结束语

本文尝试利用SAT方法进一步加速差分特征的搜索，通过改进边界条件从而降低搜索空间。密码分析者经常使用STP以及CryptoMiniSat搜索差分特征，因此本文研究了线程数以及询问条件的加速效果，并实验测试了线程数以及询问条件的加速效果。根据实验结果发现，线程数对搜索差分特征的耗时影响较大，而询问条件对搜索差分特征的耗时影响较小。此外，本文提出了一种选择线程数的策略，利用该搜索策略，首次获得了HIGHT的11轮最优差分特征的紧致概率，且结果是已有最优的结果。希望本文提出的搜索策略不仅有助于评估分组密码抗差分分析的安全性，而且有助于分组密码的设计。

[1] BIHAM E, SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[J]. Journal of Cryptology, 1991, 4(1): 3-72.

[2] MATSUI M. On correlation between the order of S-boxes and the strength of DES[C]//Workshop on the Theory and Application of Cryptographic Techniques. 1994: 366-375.

[3] BIRYUKOV A, ROY A, VELICHKOV V. Differential analysis of block ciphers SIMON and SPECK[C]//International Workshop on Fast Software Encryption. 2014: 546-570.

[4] BIRYUKOV A, VELICHKOV V, LE C Y. Automatic search for the best trails in ARX: application to block cipher speck[C]//Inte- rnational Conference on Fast Software Encryption. 2016: 289-310.

[5] LIU Z B, LI Y Q, WANG M S. Optimal differential trails in SIMON-like ciphers[J]. IACR Transactions on Symmetric Cryptology, 2017: 358-379.

[6] LIU Z B, LI Y Q, JIAO L, et al. A new method for searching optimal differential and linear trails in ARX ciphers[J]. IEEE Transactions on Information Theory, 2020, 67(2): 1054-1068.

[7] MOUHA N, WANG Q J, GU D W, et al. Differential and linear cryptanalysis using mixed-integer linear programming[C]//Int- ernational Conference on Information Security and Cryptology. 2011: 57-76.

[8] FU K, WANG M Q, GUO Y H, et al. MILP-based automatic search algorithms for differential and linear trails for speck[C]//International Conference on Fast Software Encryption. 2016: 268-288.

[9] XIANG Z J, ZHANG W T, BAO Z Z, et al. Applying MILP method to searching integral distinguishers based on division property for 6 lightweight block ciphers[C]//International Conference on the Theory and Application of Cryptology and Information Security. 2016: 648-678.

[10] CUI T T, JIA K T, FU K, et al. New automatic search tool for impossible differentials and zero-correlation linear approximations[J]. Cryptology ePrint Archive, 2016.

[11] SASAKI Y, TODO Y. New impossible differential search tool from design and cryptanalysis aspects[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. 2017: 185-215.

[12] MOUHA N, PRENEEL B. Towards finding optimal differential characteristics for ARX: application to Salsa20[J]. IACR Cryptology ePrint Archive, 2013, (2013): 328.

[13] KÖLBL S, LEANDER G, TIESSEN T. Observations on the SIMON block cipher family[C]//Annual Cryptology Conference. 2015: 161-185.

[14] ANKELE R, KÖLBL S. Mind the gap-a closer look at the security of block ciphers against differential cryptanalysis[C]//International Conference on Selected Areas in Cryptography. 2018: 163-190.

[15] ROH D Y, KOO B W, JUNG Y H, et al. Revised version of block cipher CHAM[C]//International Conference on Information Security and Cryptology. 2019: 1-19.

[16] 韩亚. 基于SAT/SMT自动搜索三类分组密码区分器研究[D]. 北京: 中国科学院大学, 2018.

HAN Y. Automatically search for three types of block cipher distinguishers based on SAT/SMT solver[D]. Beijing: University of Chinese Academy of Sciences, 2018.

[17] LIU Y W, WAND Q J, RIJMEN V. Automatic search of linear trails in ARX with applications to SPECK and Chaskey[C]//International Conference on Applied Cryptography and Network Security. 2016: 485-499.

[18] SUN L, WANG W, WANF M Q. Automatic search of bit-based division property for ARX ciphers and word-based division property[C]//International Conference on the Theory and Application of Cryptology and Information Security. 2017: 128-157.

[19] SASAKI Y, TODO Y. New algorithm for modeling S-box in MILP based differential and division trail search[C]//International Conference for Information Technology and Communications. 2017: 150-165.

[20] ZHANG Y J, SUN S W, CAI J H, et al. Speeding up MILP aided differential characteristic search with Matsui’s strategy[C]//Inter- national Conference on Information Security. 2018: 101-115.

[21] ZHOU C N, ZHANG W T, DING T Y, et al. Improving the MILP-based security evaluation algorithm against differential/linear cryptanalysis using a divide-and-conquer approach[J]. IACR Transactions on Symmetric Cryptology, 2019: 438-469.

[22] BOURA C, COGGIA D. Efficient MILP modelings for Sboxes and linear layers of SPN ciphers[C]//IACR Transactions on Symmetric Cryptology. 2020: 327-361.

[23] SONG L, HUANG Z J, YANG Q Q. Automatic differential analysis of ARX block ciphers with application to SPECK and LEA[C]//Australasian Conference on Information Security and Privacy. 2016: 379-394.

[24] SUN L, WANG W, WANG M Q. Accelerating the search of differential and linear characteristics with the SAT method[C]//IACR Transactions on Symmetric Cryptology. 2021: 269-315.

[25] GANESH V, DILL D L. A decision procedure for bit-vectors and arrays[C]//International Conference on Computer Aided Verification. 2007: 519-531.

[26] SOOS M, NOHL K, CASTELLUCCIA C. Extending SAT solvers to cryptographic problems[C]//International Conference on Theory and Applications of Satisfiability Testing. 2009: 244-257.

[27] LIPMAA H, MORIAI S. Efficient algorithms for computing differential properties of addition[C]//International Workshop on Fast Software Encryption. 2001: 336-350.

[28] BEAULIEU R, SHORS D, SMITH J, et al. The SIMON and SPECK lightweight block ciphers[C]//Proceedings of the 52nd Annual Design Automation Conference. 2015: 1-6.

[29] HONG D J, SUNG J C, HONG S H, et al. HIGHT: a new block cipher suitable for low-resource device[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2006: 46-59.

[30] EÉN N, SÖRENSSON N. An extensible SAT-solver[C]//Inte- rnational Conference on Theory and Applications of Satisfiability Testing. 2003: 502-518.

Further accelerating the search of differential characteristics based on the SAT method

XU Zheng1,2

1. State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China 2. School of Cyber Security, University of Chinese Academy of Sciences, Beijing 100049, China

differential cryptanalysis, differential characteristics, automatic search, SAT solver

TP309.7

A

10.11959/j.issn.2096−109x.2022066

2021−11−15；

2022−03−30

许峥，xuzheng@iie.ac.cn

国家自然科学基金（61772516，61772517）

The National Natural Science Foundation of China (61772516, 61772517)

许峥.基于SAT方法进一步加速差分特征的搜索[J]. 网络与信息安全学报, 2022, 8(5): 129-139.

Format: XU Z. Further accelerating the search of differential characteristics based on the SAT method[J]. Chinese Journal of Network and Information Security, 2022, 8(5): 129-139.

许峥（1992− ），男，河南郑州人，中国科学院信息工程研究所博士生，主要研究方向为分组密码的分析与设计。