基于鸽群的鲁棒强化学习算法
张明英,华冰,张宇光,李海东,郑墨泓
基于鸽群的鲁棒强化学习算法
张明英1,华冰2,张宇光1,李海东1,郑墨泓3
(1. 中国电子技术标准化研究院,北京 100007;2. 南京航空航天大学航天学院,江苏 南京 211106;3. 中国电子科技集团公司第七研究所,广东 广州 510000)
强化学习是一种人工智能算法,具有计算逻辑清晰、模型易扩展的优点,可以在较少甚至没有先验信息的前提下,通过和环境交互并最大化值函数,调优策略性能,有效地降低物理模型引起的复杂性。基于策略梯度的强化学习算法目前已成功应用于图像智能识别、机器人控制、自动驾驶路径规划等领域。然而强化学习高度依赖采样的特性决定了其训练过程需要大量样本来收敛,且决策的准确性易受到与仿真环境中不匹配的轻微干扰造成严重影响。特别是当强化学习应用于控制领域时,由于无法保证算法的收敛性,难以对其稳定性进行证明,为此,需要对强化学习进行改进。考虑到群体智能算法可通过群体协作解决复杂问题,具有自组织性及稳定性强的特征,利用其对强化学习进行优化求解是一个提高强化学习模型稳定性的有效途径。结合群体智能中的鸽群算法,对基于策略梯度的强化学习进行改进:针对求解策略梯度时存在迭代求解可能无法收敛的问题,提出了基于鸽群的强化学习算法,以最大化未来奖励为目的求解策略梯度,将鸽群算法中的适应性函数和强化学习结合估计策略的优劣,避免求解陷入死循环,提高了强化学习算法的稳定性。在具有非线性关系的两轮倒立摆机器人控制系统上进行仿真验证,实验结果表明,基于鸽群的强化学习算法能够提高系统的鲁棒性,降低计算量,减少算法对样本数据库的依赖。
鸽群算法;强化学习;策略梯度;鲁棒性
0 引言
强化学习是一种典型的人工智能算法,具有需要先验信息少、计算逻辑清晰等优点,适用于机器人控制、路径规划、游戏策略等问题求解,近年来在多个领域获得了广泛应用[1-7]。当强化学习应用于控制领域时,具有仅需要少量先验信息、甚至无须对物理系统建模的优点,能够有效地降低物理模型引起的复杂性,且可以灵活地处理不确定性问题。然而,强化学习应用于控制领域存在计算量较大和鲁棒性较差的问题,且由于无法保证算法的收敛性,难以对其进行稳定性证明。
强化学习主要包括3类[8-15]:策略梯度(policy gradient)、值函数学习、结合两者的演员−评论家(actor-critic)模型。基于策略梯度方法因直接优化策略,可实现随机策略(stochastic policy)的求解,且具有较好的收敛性。因此,基于策略梯度的强化学习算法得到了广泛的应用,其主要计算复杂度体现在策略梯度的求解。群体智能算法启发于具有社会行为的昆虫群体,对其行为进行模拟,包括狼群算法、粒子群算法、蚁群算法、遗传算法、鸽群算法等。鸽群算法是一种新型优化计算方法,具有执行效率高的优点。本文采用鸽群算法对基于确定性策略梯度的强化学习算法进行改进,一方面基于鸽群算法的演化规律减少迭代过程,从而优化求解其策略梯度,减小计算量以及对样本数据库的依赖;另一方面,通过及时纠正迭代的方向,增强系统鲁棒性。
1 智能算法模型
1.1 强化学习模型
基于策略梯度的强化学习根据式(1)更新策略。
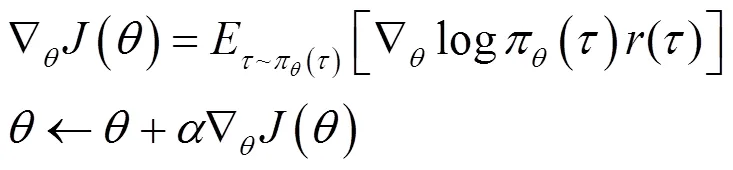
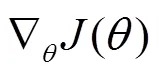
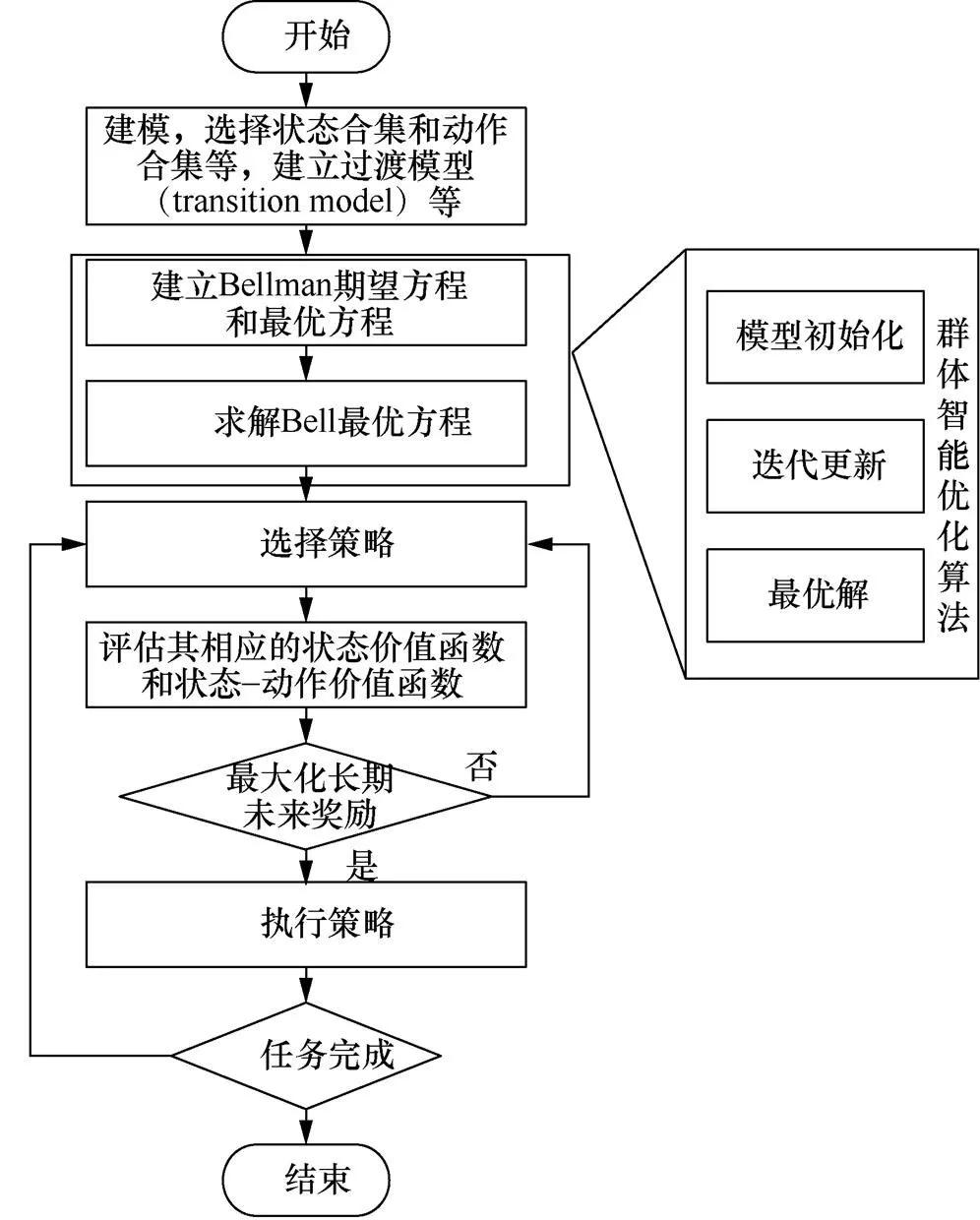
图1 基于群体智能优化算法改进强化学习算法的流程
Figure 1 Process of improving reinforcement learning algorithm based on swarm intelligence optimization algorithm
1.2 经典鸽群算法模型
经典鸽群算法[16-20]是基于鸽子在归巢过程中的动态导航过程发展而成的,鸽子依靠地球磁场以及太阳的位置进行导航,在到达目的地附近时依靠地标进行导航。鸽群算法存在两个算子:地图指南针算子和地标算子。
1.2.1 地图指南针算子
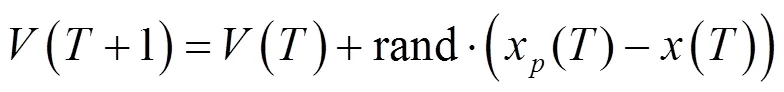
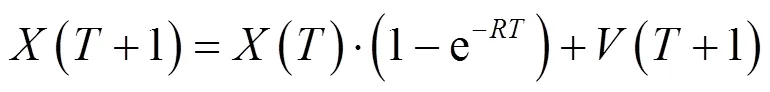
1.2.2 地标算子
经典鸽群算法在经过一定次数的地图指南针算子的迭代之后,将切换至地标算子进行运算以达到快速收敛以及对之前迭代中产生的精英个体筛选保留的目的。其演化规律可表达如下:
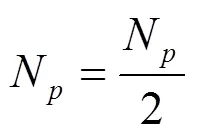
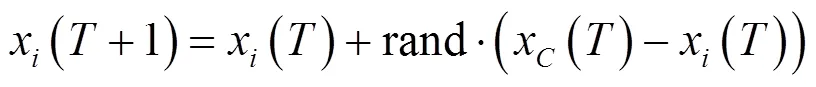
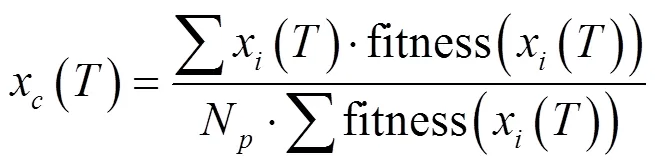
2 基于鸽群改进的强化学习方法
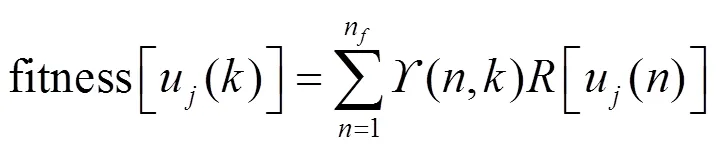
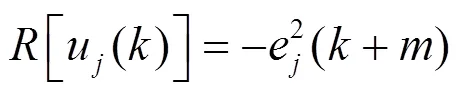
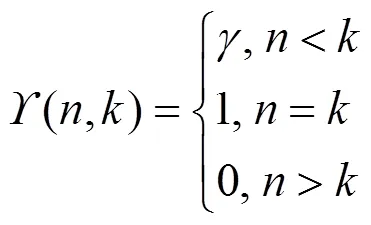
基于鸽群改进的强化学习算法流程如图2所示。
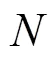
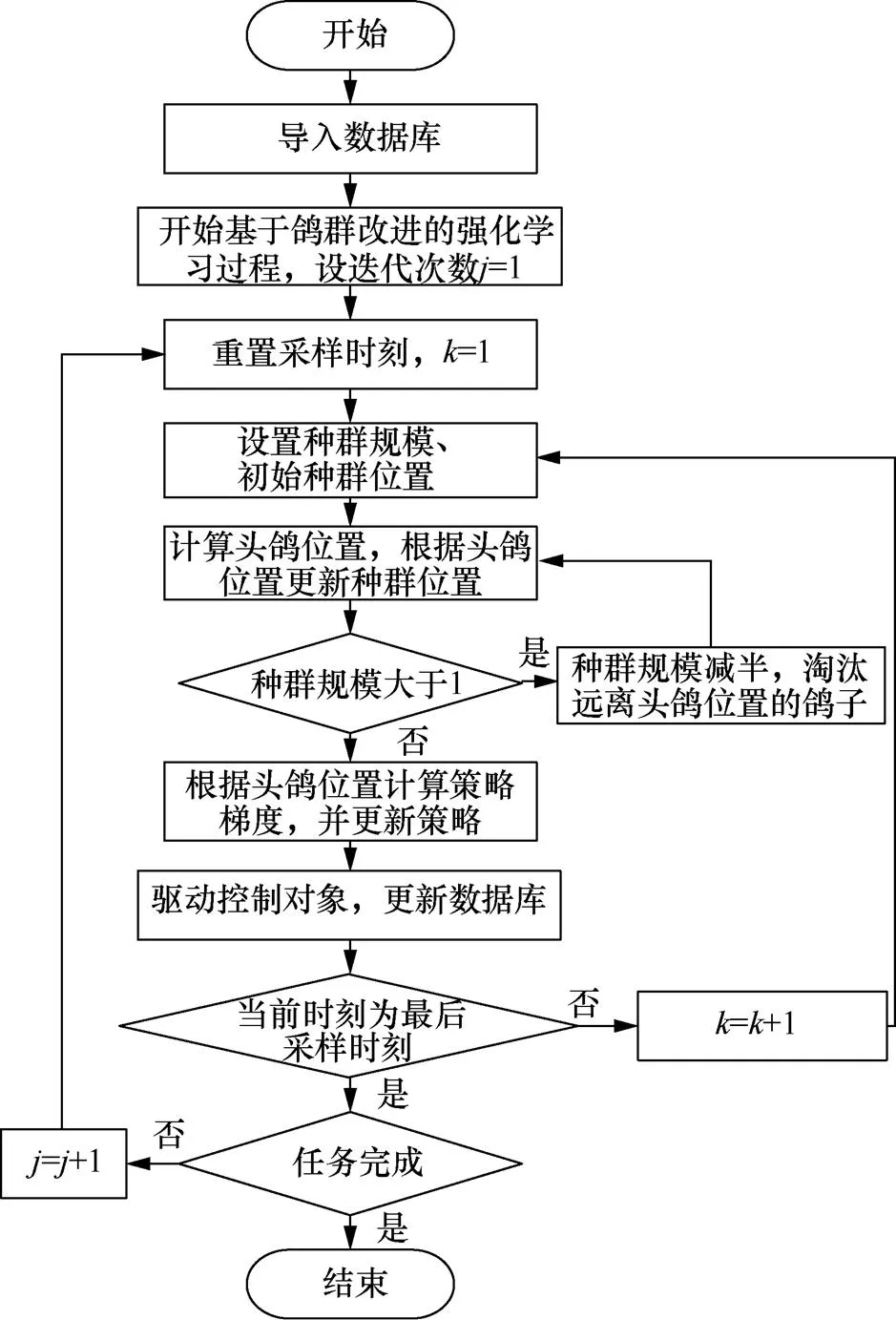
图2 基于鸽群改进的强化学习方法流程
Figure 2 Process of improved reinforcement learning method based on pigeon-inspired optimization
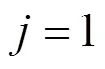
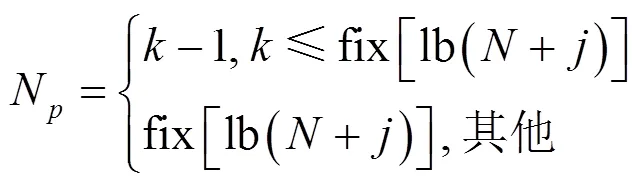
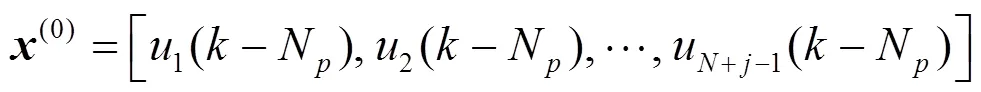
步骤6 计算头鸽位置。
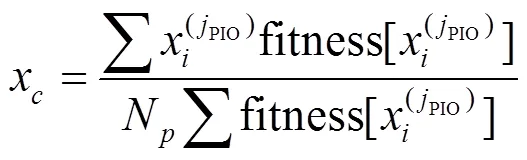
步骤7 更新种群位置和鸽群迭代次数。
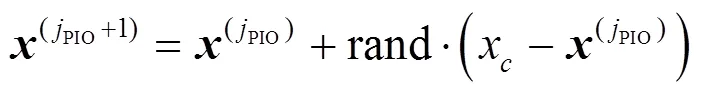
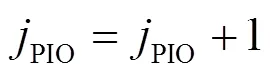
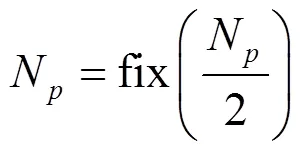
步骤9 计算策略梯度。
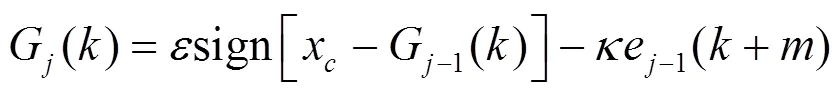
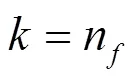
3 仿真建模
3.1 仿真模型
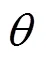
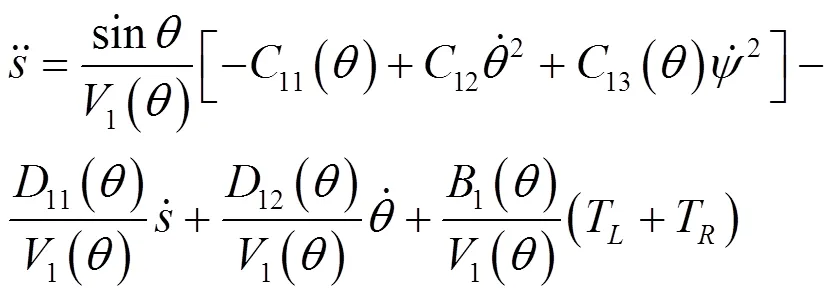
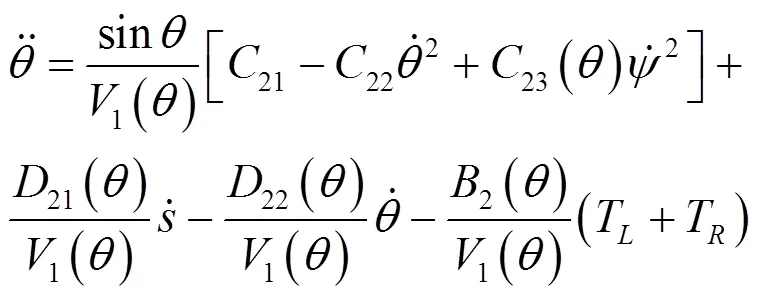
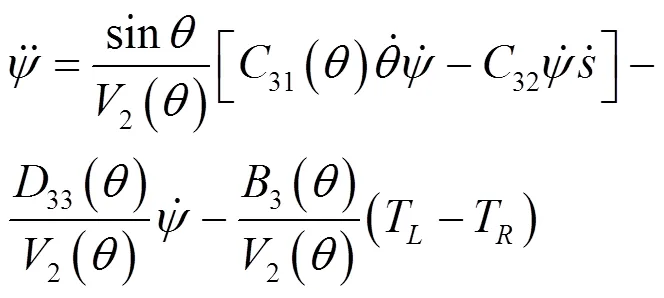
其中,
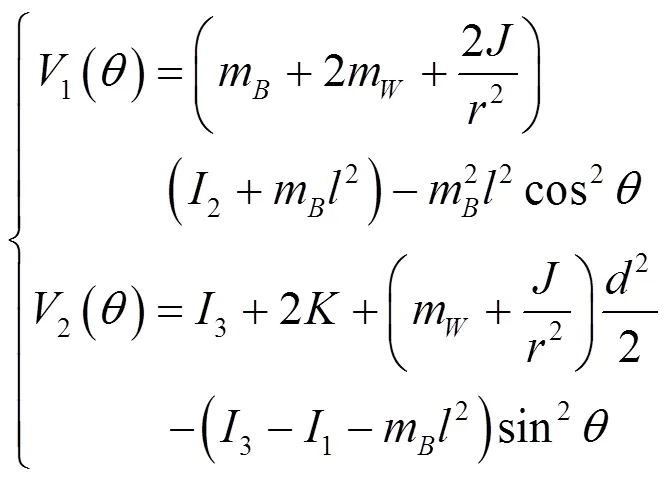
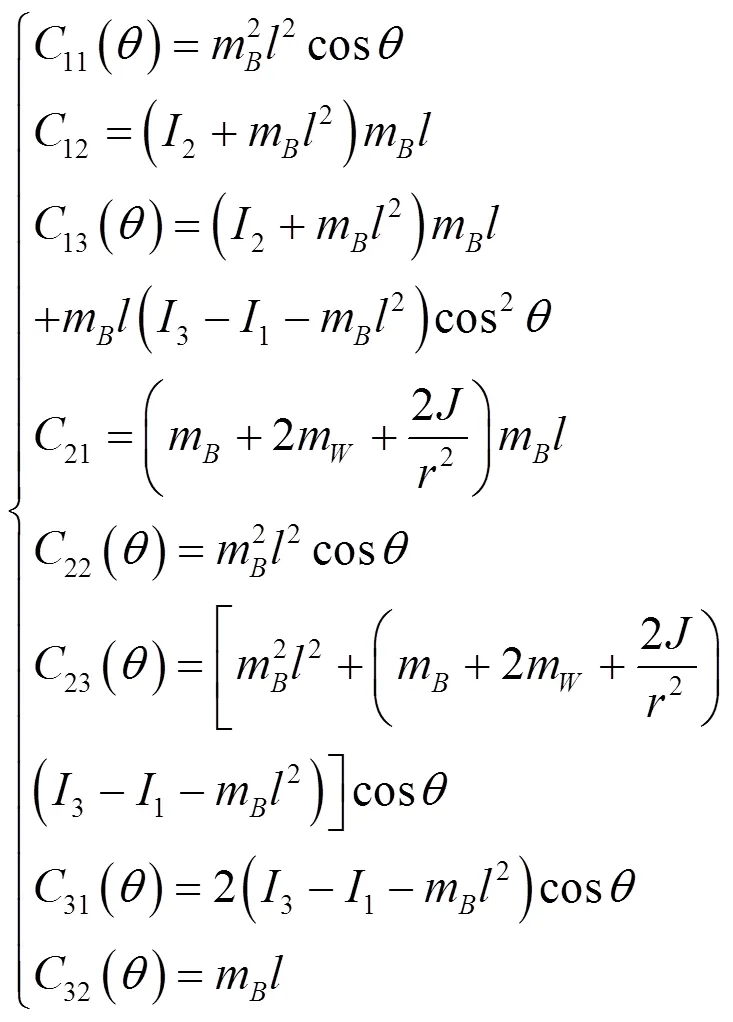
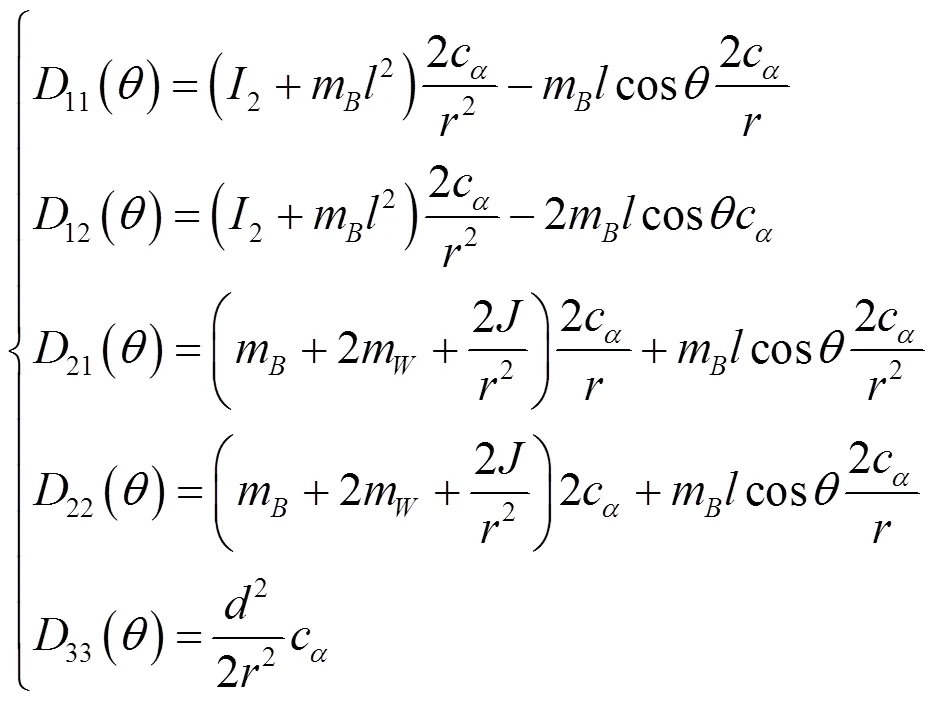
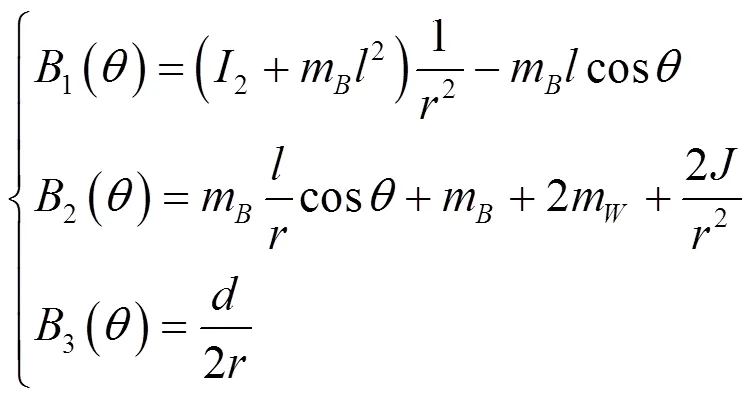
考虑沿直线运动的情况,即
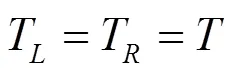
需要注意的是,基于鸽群的强化学习算法无须对物理系统进行建模,式(17)~式(24)的两轮倒立摆机器人模型仅用于搭建数值仿真中的动力学与运动学模块。
(1)数据库与任务匹配
(2)数据库与任务不匹配
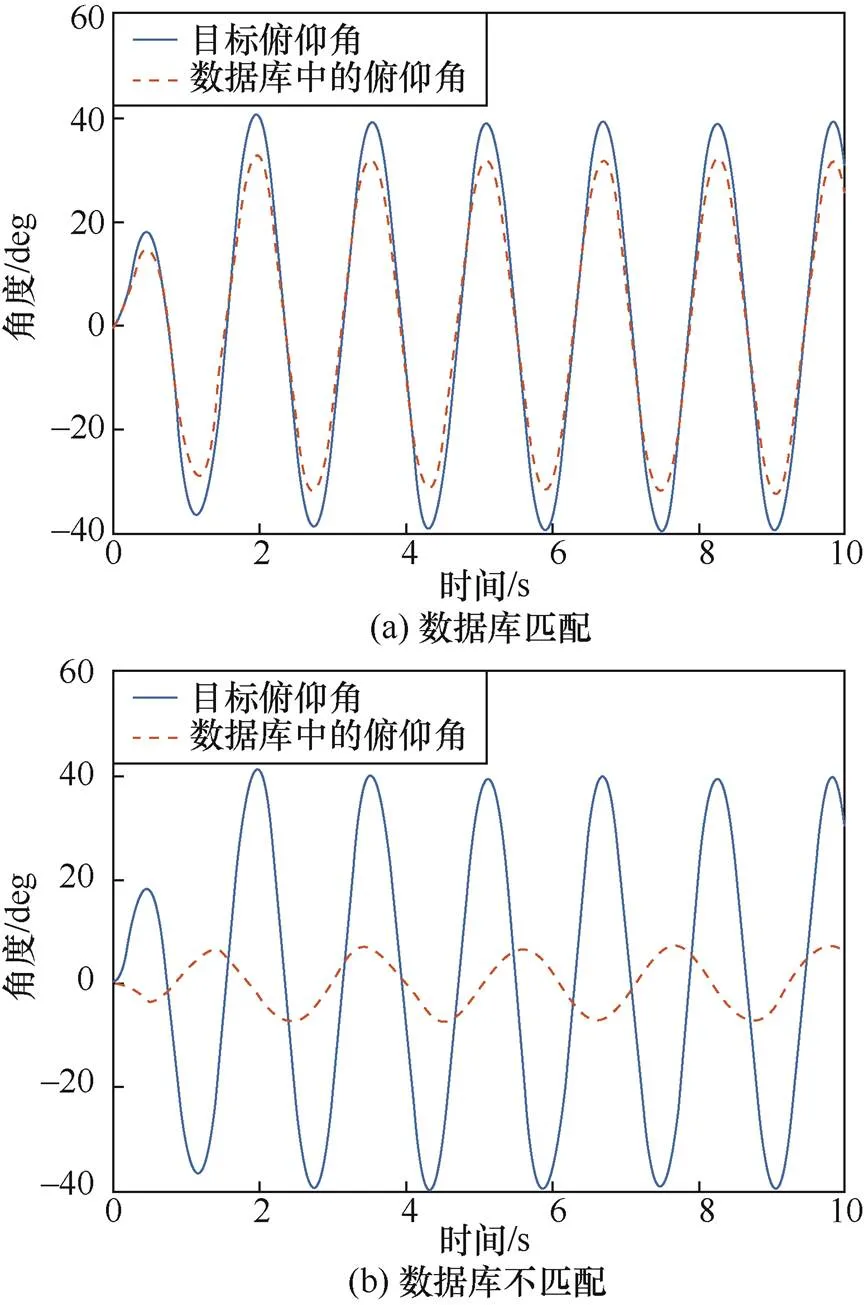
图3 数据库样例
Figure 3 Sample database
3.2 仿真分析
本节验证上述基于鸽群改进的强化学习算法应用于控制任务时的性能,并与无改进基于策略梯度的强化学习算法进行对比,仿真参数如表1所示。其中,数据库采用式(17)~式(24)构建的物理系统输入指定的控制力矩后产生的数据进行构建。

表1 仿真参数
两轮倒立摆机器人系统参数如表2所示。
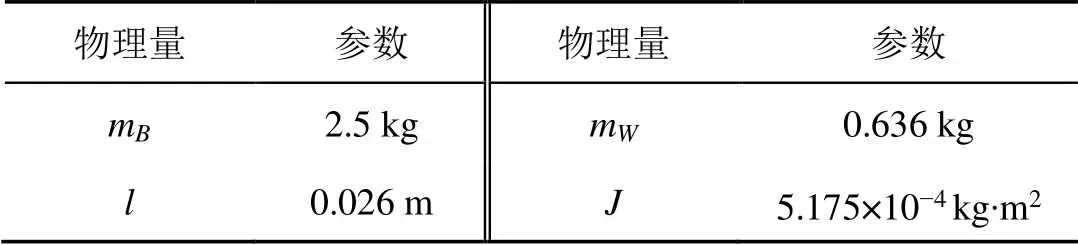
表2 两轮倒立摆机器人系统参数
仿真要求两轮倒立摆机器人跟踪随时间变化的目标姿态。
算例1的仿真结果如图4所示,在数据库与任务匹配的前提下,基于鸽群的鲁棒强化学习算法能够完成控制任务。
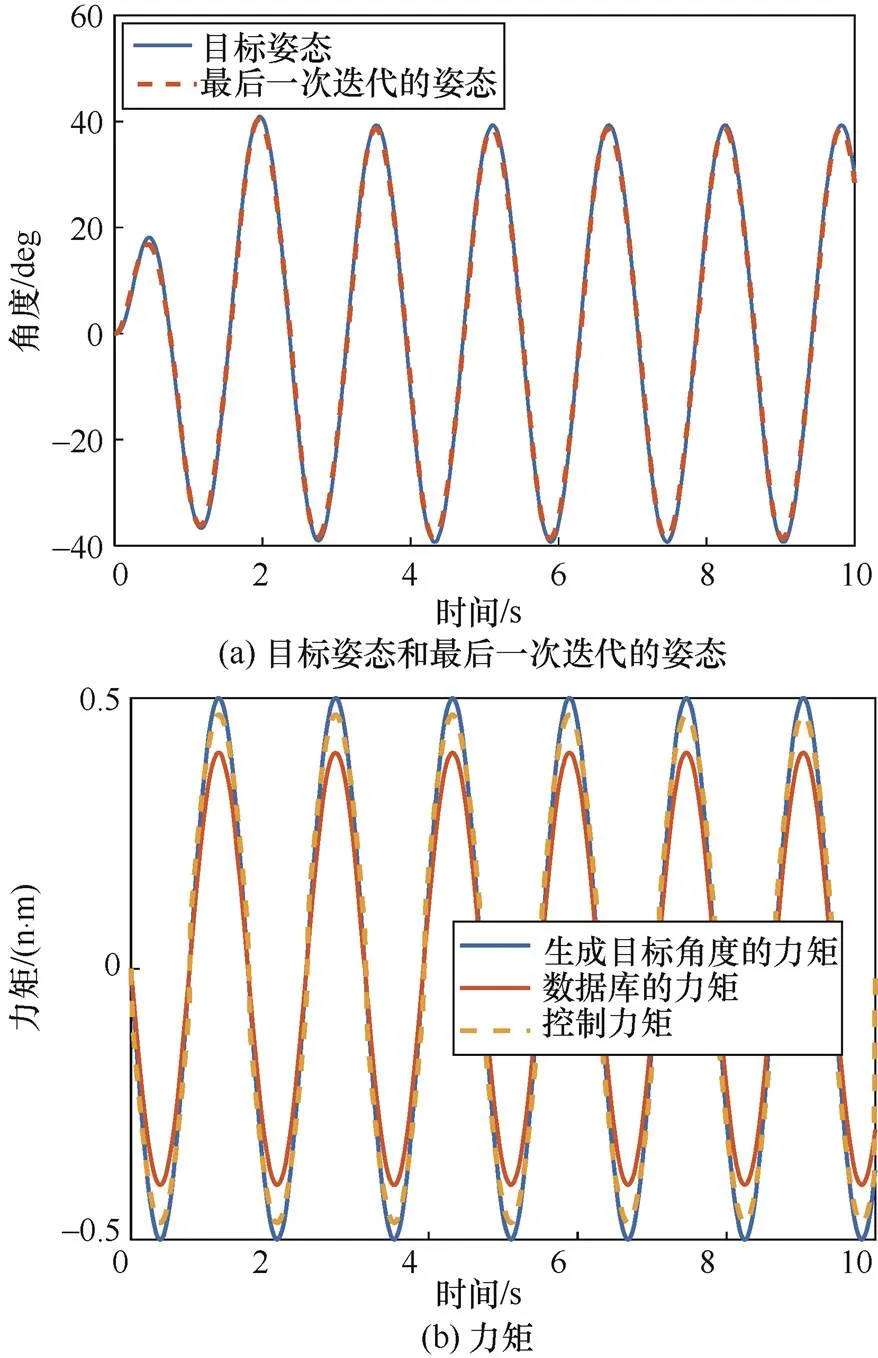
图4 算例1的仿真结果
Figure 4 Simulation results of example 1
算例2的仿真结果如图5所示,由图5(b)可知,数据库与任务不匹配,但采用基于鸽群改进的强化学习算法控制后,机器人仍能完成控制任务。
算例3的仿真结果如图6所示,在数据库与任务匹配时,基于策略梯度的强化学习算法可以完成控制任务。
算例4的仿真结果如图7所示,在数据库与任务不匹配时,基于策略梯度的强化学习算法难以判断控制力矩更新的方向,无法完成控制任务。
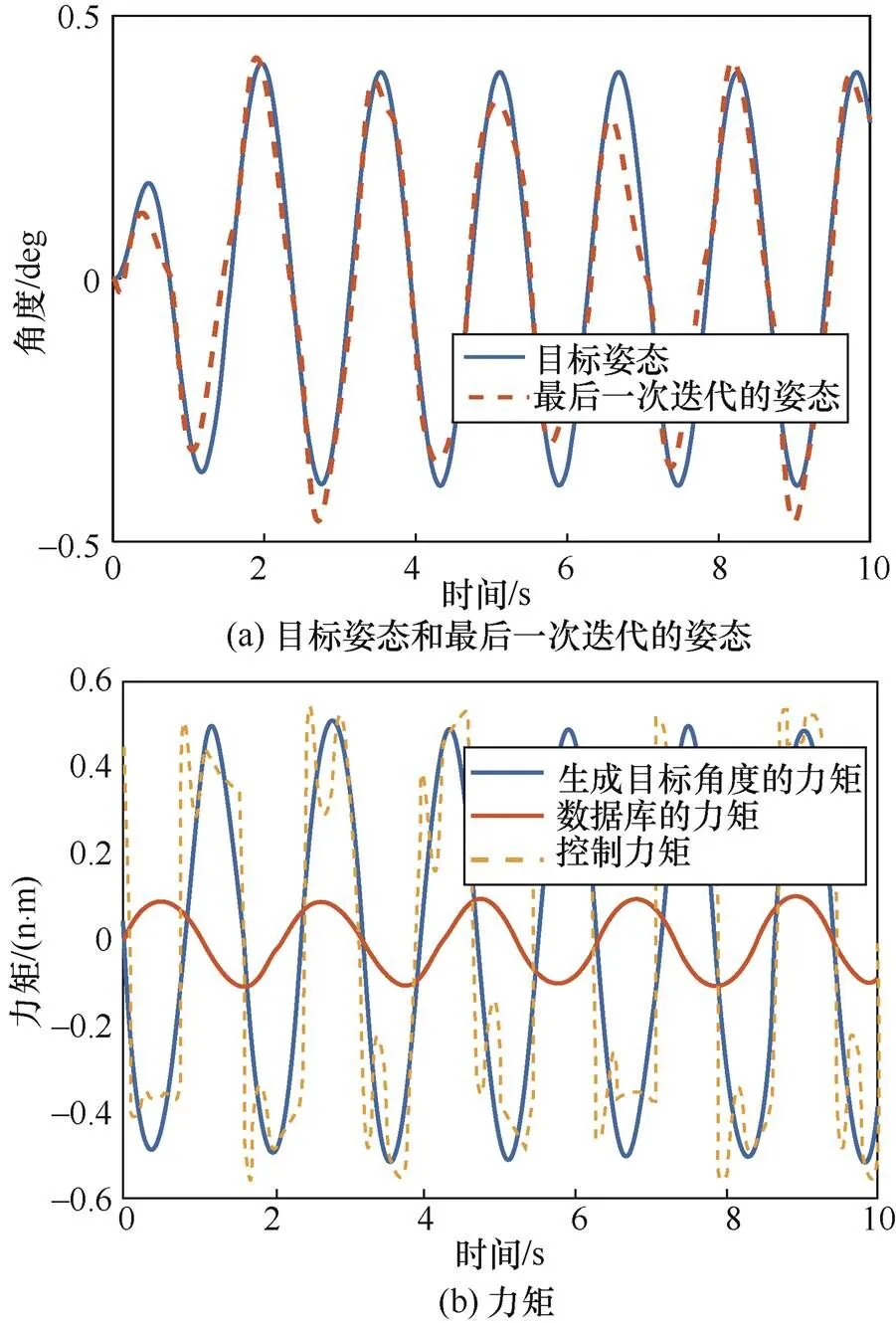
图5 算例2的仿真结果
Figure 5 Simulation results of example 2
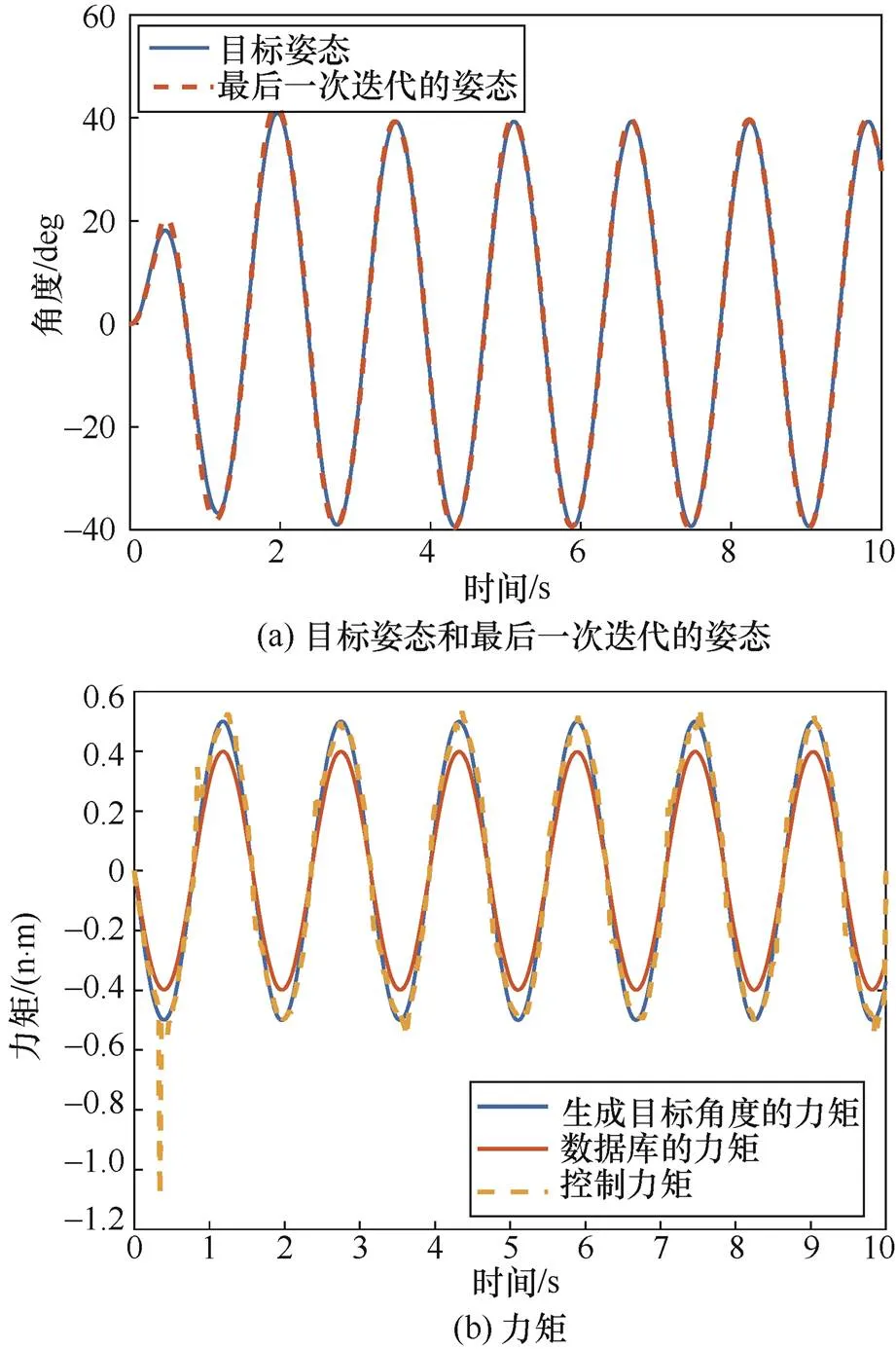
图6 算例3的仿真结果
Figure 6 Simulation results of example 3
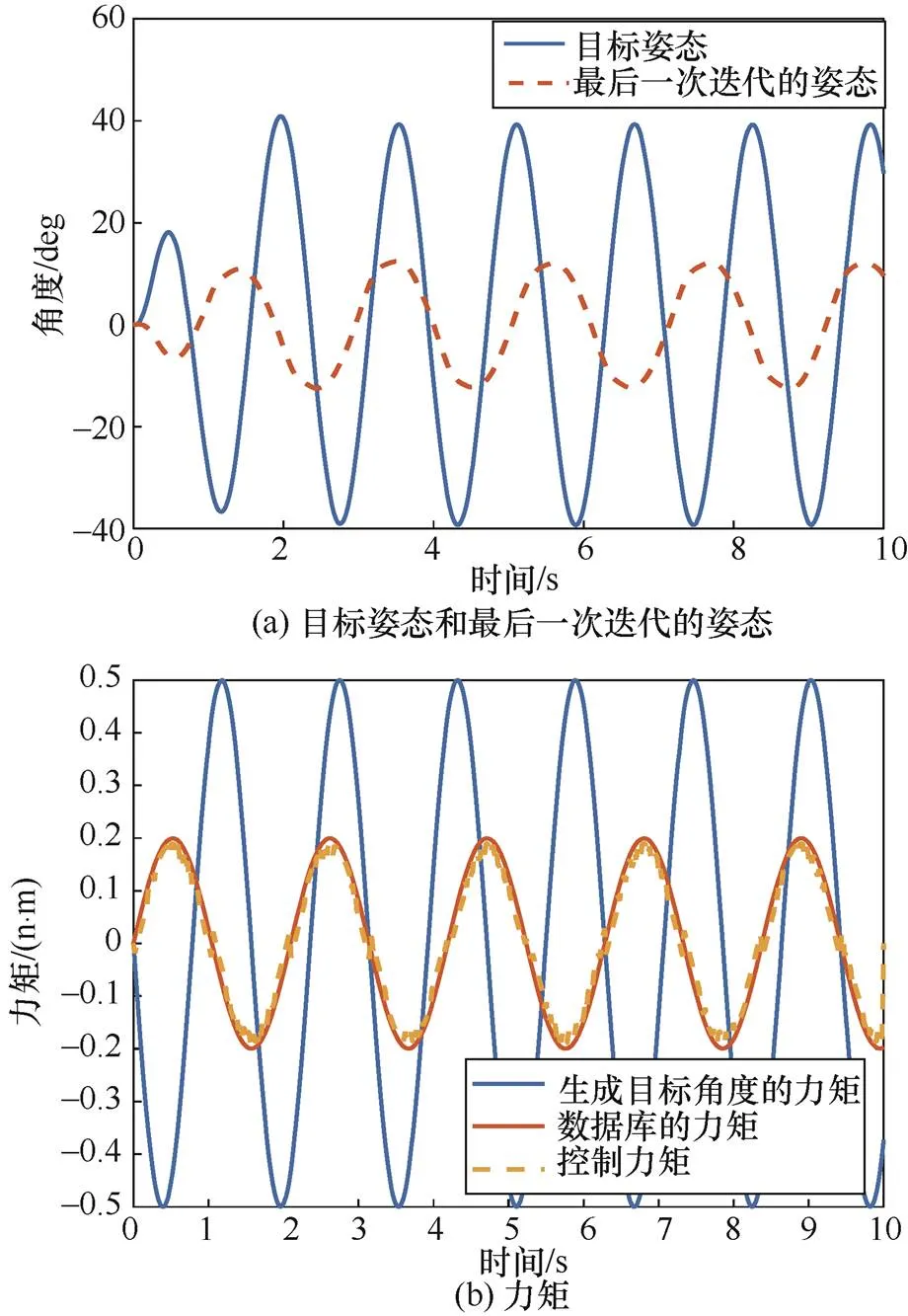
图7 算例4的仿真结果
Figure 7 Simulation results of example 4
算例1~算例4的控制力矩误差随时间变化如图8所示,无论数据库与任务匹配与否,基于鸽群的鲁棒强化学习算法都能得到较小的误差;基于策略梯度的强化学习算法在数据库与任务匹配时存在误差状况不稳定的情况,在数据库与任务不匹配时误差明显,不能完成控制任务。
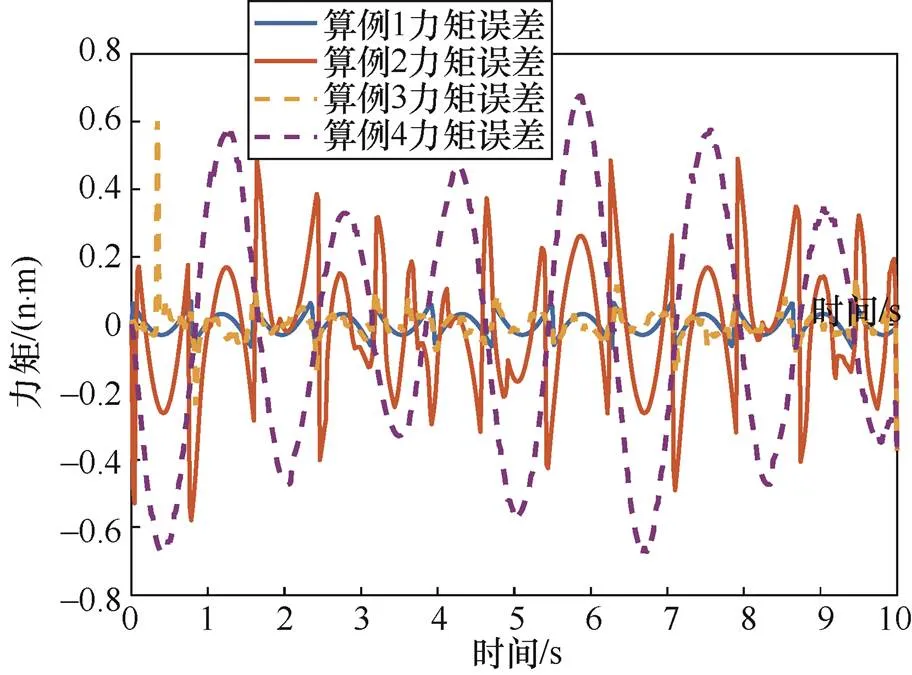
图8 算例1~算例4的控制力矩误差
Figure 8 Control torque errors from example 1 to example 4
算例1~算例4的对比如表3所示,得到以下结论。
1) 当数据库与任务匹配时,基于鸽群的鲁棒强化学习算法和基于策略梯度的强化学习算法均能完成控制任务。

表3 算例对比
2) 当数据库与任务不匹配时,基于鸽群的鲁棒强化学习算法仍能较好地完成控制任务,而基于策略梯度的强化学习算法无法完成控制任务。
3) 针对同一个控制任务,基于鸽群的鲁棒强化学习算法完成1次训练的时间小于基于策略梯度的强化学习算法。
综上所述,相比基于策略梯度的强化学习算法,基于鸽群改进的强化学习算法具有以下优点。
1) 计算量小,并且不存在无法判断策略梯度的情况,无须强制跳出循环。
2) 基于鸽群的鲁棒强化学习算法的收敛速度更快,控制精度更高,因此,基于鸽群的鲁棒强化学习算法的鲁棒性优于基于策略梯度的强化学习算法。
3) 当任务时间较长时,由于迭代过程更复杂,基于鸽群的鲁棒强化学习算法的计算量稍大,但可以通过修改种群规模减小计算量。
4 结束语
强化学习是一种基于机器学习的算法,具有需要先验信息少等优点,适用于图像识别、控制、路径规划等领域。当强化学习应用于控制领域时,能够有效地降低物理模型引起的复杂性,且灵活地处理不确定性问题。然而,强化学习应用于控制领域存在计算量较大和鲁棒性较差的问题,且由于无法保证算法的收敛性,难以对其进行稳定性证明。本文采用鸽群算法对强化学习进行改进,优化算法性能,采用鸽群改进强化学习算法能够大幅度增加鲁棒性,降低了计算量,同时减少了算法对样本数据库的依赖。
[1] PETERS J, SCHAAL S. Policy gradient methods for robotics[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2006: 2219-2225.
[2] BAUM Y, AMICO M, HOWELL S, et al. Experimental deep reinforcement learning for error-robust gate-set design on a superconducting quantum computer[J]. PRX Quantum, 2021, 2(4): 040324.
[3] HUA J, ZENG L, LI G, et al. Learning for a robot: deep reinforcement learning, imitation learning, transfer learning[J]. Sensors, 2021, 21(4): 1278.
[4] SIVAK V V, EICKBUSCH A, LIU H, et al. Model-free quantum control with reinforcement learning[J]. Physical Review X, 2022, 12(1): 011059.
[5] AGARWAL N, HAZAN E, MAJUMDAR A, et al. A regret minimization approach to iterative learning control[C]//International Conference on Machine Learning (PMLR). 2021: 100-109.
[6] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Advances in Neural Information Processing Systems. 2012: 1097-1105.
[7] YARATS D, FERGUS R, LAZARIC A, et al. Reinforcement learning with prototypical representations[C] //International Conference on Machine Learning (PMLR). 2021: 11920-11931.
[8] DAHL G E, YU D, DENG L, et al. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011: 30-42.
[9] HAOXIANG W, SMYS S. Overview of configuring adaptive activation functions for deep neural networks—a comparative study[J]. Journal of Ubiquitous Computing and Communication Technologies (UCCT), 2021, 3(1): 10-22.
[10] MISHRA A, LATORRE J A, Pool J, et al. Accelerating sparse deep neural networks[J]. arXiv preprint arXiv:2104.08378, 2021.
[11] SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of go with deep neural networks and tree search[J]. Nature, 2016, 529: 484.
[12] VINYALS O, BABUSCHKIN I, CZARNECKI W M, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning[J]. Nature, 2019, 575: 350-354.
[13] HEESS N, WAYNE G, SILVER D, et al. Learning continuous control policies by stochastic value gradients[C]//Advances in Neural Information Processing Systems. 2015: 28
[14] CHEN Z, CHEN B, XIE S, et al. Efficiently training on-policy actor-critic networks in robotic deep reinforcement learning with demonstration-like sampled exploration[C]//2021 3rd International Symposium on Robotics & Intelligent Manufacturing Technology (ISRIMT). 2021: 292-298.
[15] WANG C, LING Y. Actor-critic tracking with precise scale estimation and advantage function[J]. Journal of Physics Conference Series, 2021, 1827(1): 012064.
[16] ZHANG S, DUAN H. Gaussian pigeon-inspired optimization approach to orbital spacecraft formation reconfiguration [J]. Chinese Journal of Aeronautics, 2015, 28 (1): 200-205.
[17] ZHANG B, DUAN H. Three-dimensional path planning for uninhabited combat aerial vehicle based on predator-prey pigeon-inspired optimization in dynamic environment[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2017, 14 (1): 97-107.
[18] 周雨鹏. 基于鸽群算法的函数优化问题求解[D]. 长春: 东北师范大学, 2016.
ZHOU Y P. Function optimization problem solving based on pigeon swarm algorithm[D]. Changchun: Northeast Normal University, 2016.
[19] 顾清华, 孟倩倩. 优化复杂函数的粒子群−鸽群混合优化算法[J].计算机工程与应用, 2019, 55(22): 46-52.
GU Q H, MENG Q Q. Hybrid particle swarm optimization and pigeon—inspired optimization algorithm for solving complex functions[J]. Computer Engineering and Applications, 2019, 55(22): 46-52.
[20] 胡耀龙, 冯强, 海星朔, 等. 基于自适应学习策略的改进鸽群优化算法[J]. 北京航空航天大学学报, 2020, 46(12): 2348-2356.
HU Y L, FENG Q, HAI X S, et al. Improved pigeon-inspired optimization algorithm based on adaptive learning strategy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(12) : 2348-2356.
Robust reinforcement learning algorithm based on pigeon-inspired optimization
ZHANG Mingying1, HUA Bing2, ZHANG Yuguang1, LI Haidong1, ZHENG Mohong3
1. China Electronics Standardization Institute, Beijing 100007, China 2. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China 3. The 7th Research Institute of China Electronics Technology Group Corporation, Guangzhou 510000, China
Reinforcement learning(RL) is an artificial intelligence algorithm with the advantages of clear calculation logic and easy expansion of the model. Through interacting with the environment and maximizing value functions on the premise of obtaining little or no prior information, RL can optimize the performance of strategies and effectively reduce the complexity caused by physical models . The RL algorithm based on strategy gradient has been successfully applied in many fields such as intelligent image recognition, robot control and path planning for automatic driving. However, the highly sampling-dependent characteristics of RL determine that the training process needs a large number of samples to converge, and the accuracy of decision making is easily affected by slight interference that does not match with the simulation environment. Especially when RL is applied to the control field, it is difficult to prove the stability of the algorithm because the convergence of the algorithm cannot be guaranteed. Considering that swarm intelligence algorithm can solve complex problems through group cooperation and has the characteristics of self-organization and strong stability, it is an effective way to be used for improving the stability of RL model. The pigeon-inspired optimization algorithm in swarm intelligence was combined to improve RL based on strategy gradient. A RL algorithm based on pigeon-inspired optimization was proposed to solve the strategy gradient in order to maximize long-term future rewards. Adaptive function of pigeon-inspired optimization algorithm and RL were combined to estimate the advantages and disadvantages of strategies, avoid solving into an infinite loop, and improve the stability of the algorithm. A nonlinear two-wheel inverted pendulum robot control system was selected for simulation verification. The simulation results show that the RL algorithm based on pigeon-inspired optimization can improve the robustness of the system, reduce the computational cost, and reduce the algorithm’s dependence on the sample database.
pigeon-inspired optimization algorithm, strengthen learning, policy gradient, robustness
TP393
A
10.11959/j.issn.2096−109x.2022064
2022−05−22;
2022−07−15
张明英,zhangmy@cesi.cn
科技创新2030重大项目(2020AAA0107804)
Science and Technology Innovation 2030 Major Project (2020AAA0107804)
张明英, 华冰, 张宇光, 等. 基于鸽群的鲁棒强化学习算法[J]. 网络与信息安全学报, 2022, 8(5): 66-74.
Format: ZHANG M Y, HUA B, ZHANG Y G, et al. Robust reinforcement learning algorithm based on pigeon-inspired optimization[J]. Chinese Journal of Network and Information Security, 2022, 8(5): 66-74.
张明英(1985−),男,广西北海人,中国电子技术标准化研究院高级工程师,主要研究方向为人工智能、知识图谱、大数据。

华冰(1978−),女,江苏南京人,南京航空航天大学副研究员,主要研究方向为飞行器导航、智能数据处理。
张宇光(1991−),男,内蒙古包头人,中国电子技术标准化研究院工程师,主要研究方向为数据安全、人工智能安全、个人信息保护、计算机视觉、视觉生成。

李海东(1992−),男,湖北孝感人,中国电子技术标准化研究院工程师,主要研究方向为人工智能安全、大数据安全、个人信息保护。
郑墨泓(1995−),女,广东潮阳人,中国电子科技集团公司第七研究所助理工程师,主要研究方向为航天器姿态控制、无人机组网。


