新的基于双混沌系统和压缩感知的图像加密算法

杨宇光，曹国栋

新的基于双混沌系统和压缩感知的图像加密算法

杨宇光，曹国栋

（北京工业大学信息学部，北京 100124）

图像加密技术在当今多媒体应用和互联网信息安全传输中发挥着重要作用，但存在一些问题。多数图像加密算法存在密文图像在传输过程中占用带宽较高、图像加密速度慢、图像加密算法没有与明文关联、没有完备密文反馈机制等问题，这些问题影响着图像加密算法的安全性和易用性。为了解决上述问题，对压缩感知技术和混沌系统进行了研究，提出了一种新的基于双混沌系统和压缩感知的明文关联的图像加密算法。采用明文图像关联密钥，将明文图像哈希值与Logistic混沌系统参数进行关联；采用离散小波变换对明文图像进行稀疏处理；通过Logistic混沌系统生成随机测量矩阵，结合压缩感知技术和随机测量矩阵对图像进行一次加密，得到中间图像；对中间图像再次进行哈希，与明文图像哈希值共同关联Rucklidge混沌系统初值；使用Rucklidge混沌系统和加密算法控制中间图像进行二次加密，得到密文图像。加密算法是一种新的明文关联加密算法，该算法使用图像自身像素值控制中间图像置乱，可以增强明文关联，建立密文反馈机制。仿真结果和性能分析表明，所提算法加密性能良好，加密后图像可按照压缩比例进行压缩，有效减小密文图像尺寸，且可以很好地抵抗已知明文攻击、选择明文攻击、差分攻击等常见攻击，优于其他常见图像加密算法。

图像加密；压缩感知；双混沌系统；明文关联；离散小波变换

0 引言

图像是互联网时代众多信息传输载体中的多媒体形式之一。然而，由于互联网的开放性和带宽资源的稀缺性，图像的安全性和传输效率问题备受关注。因此，在传输过程中对图像进行加密和压缩就显得尤为重要。图像加密技术保护图像信息不被泄露和篡改[1]，而图像压缩技术有效减少图像的冗余信息，从而减小图像的存储空间，提高其在网络中的传输效率。

压缩感知（CS，compressive sensing）是一种将高维稀疏信号通过随机采样生成低维信号的算法，其采样频率远低于奈奎斯特频率[2]，因此常被用来压缩信号。许多基于CS的加密算法被提出，且安全性和鲁棒性都被验证良好[3]。例如，文献[4]将改进的混沌映射和CS结合提出了一种快速加密算法。文献[5]结合CS和奇异值分解（SVD，singular value decomposition），提出了一种视觉有意义的图像加密算法。文献[6]结合超混沌系统提出一种有效的图像加密算法。文献[7]提出一种基于CS和三维离散余弦变换（3D-DCT，three dimensional discrete cosine transform）的三图像加密算法，算法使用2D混沌系统生成测量矩阵，分别对3幅图像进行CS，得到3幅密文图像，最终使用3D-DCT将密文图像嵌入单张彩色载体图像中。

然而，CS处理图像时，本质上是一种线性测量和压缩[8]，易遭受已知明文攻击[9]和选择明文攻击[10]。为了更好地抵抗各种攻击，本文提出了一种新的明文关联初值生成算法，进而提出了一种新的基于双混沌系统和CS的图像加密算法。仿真结果和性能分析表明所提算法可更好地抵抗已知明文攻击、选择明文攻击、差分攻击[11]等常见攻击，图像重构质量较好。

1 相关理论

（1）Logistic 混沌系统

Logistic混沌系统是一维混沌系统[12]，有着良好的混沌特性，具有对初值敏感和计算速度快等优点，定义如下：

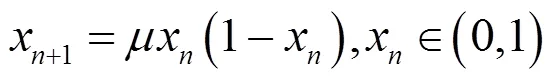
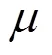
（2）Rucklidge混沌系统

Rucklidge混沌系统是一种非线性动力系统[13]，该系统对初值敏感，有着优秀的混沌特性，其表达式如下：

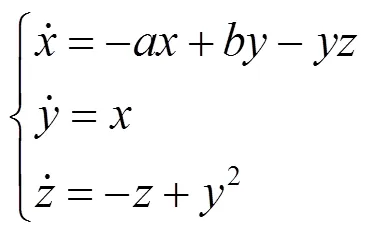
其中，、、是状态变量，、是系统参数。当系统参数=2，=6.7时，该混沌系统的最大李雅普诺夫指数为0.064 3，系统处于混沌状态。本文使用Rucklidge混沌系统控制中间图像二次加密。

2 新的图像加密算法

2.1 明文关联分块置乱算法

为了更好地抵抗选择明文攻击和差分攻击，本文提出一种新的明文关联分块置乱算法，步骤如下。

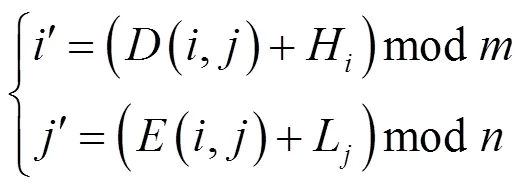
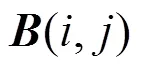
步骤3 按从左至右、从上至下的扫描方式遍历矩阵，依次循环执行步骤2，实现由矩阵向矩阵置乱。

步骤4 将矩阵和矩阵位置对调，由矩阵向矩阵进行置乱，并给定两个新的随机矩阵、替换和，重复步骤2和步骤3。

使用明文关联分块置乱算法是为了对中间图像进行置乱操作，加强置乱环节的明文关联，更好地抵抗选择明文攻击和已知明文攻击。

2.2 图像加密算法描述

2.2.1 参数生成

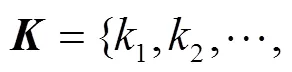
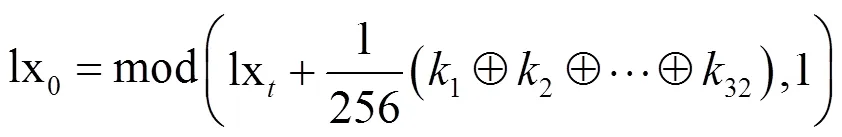
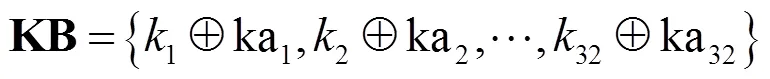
使用KB计算以下初值：

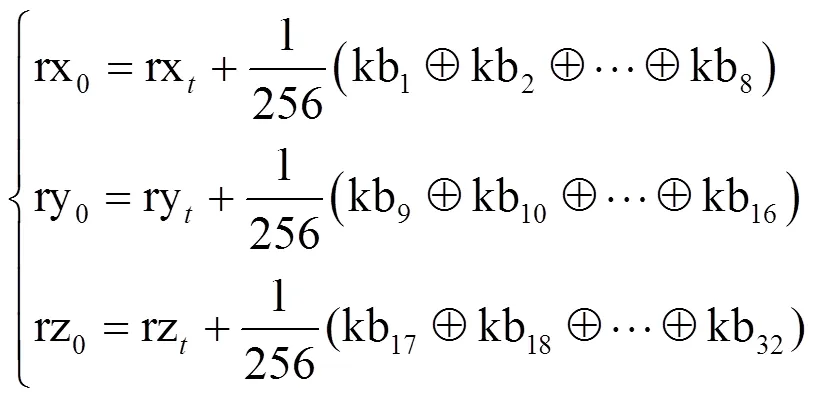
其中，rx、ry、rz是指定值。通过密文反馈机制加强明文、密文与密钥流之间的联系。

2.2.2 加密过程

图像加密流程如图1所示，具体流程如下。

2) 计算图像的SHA-256哈希值得到序列，并使用式(4)得到Logistic混沌系统初始值lx0。

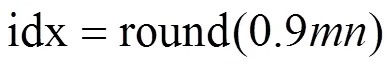
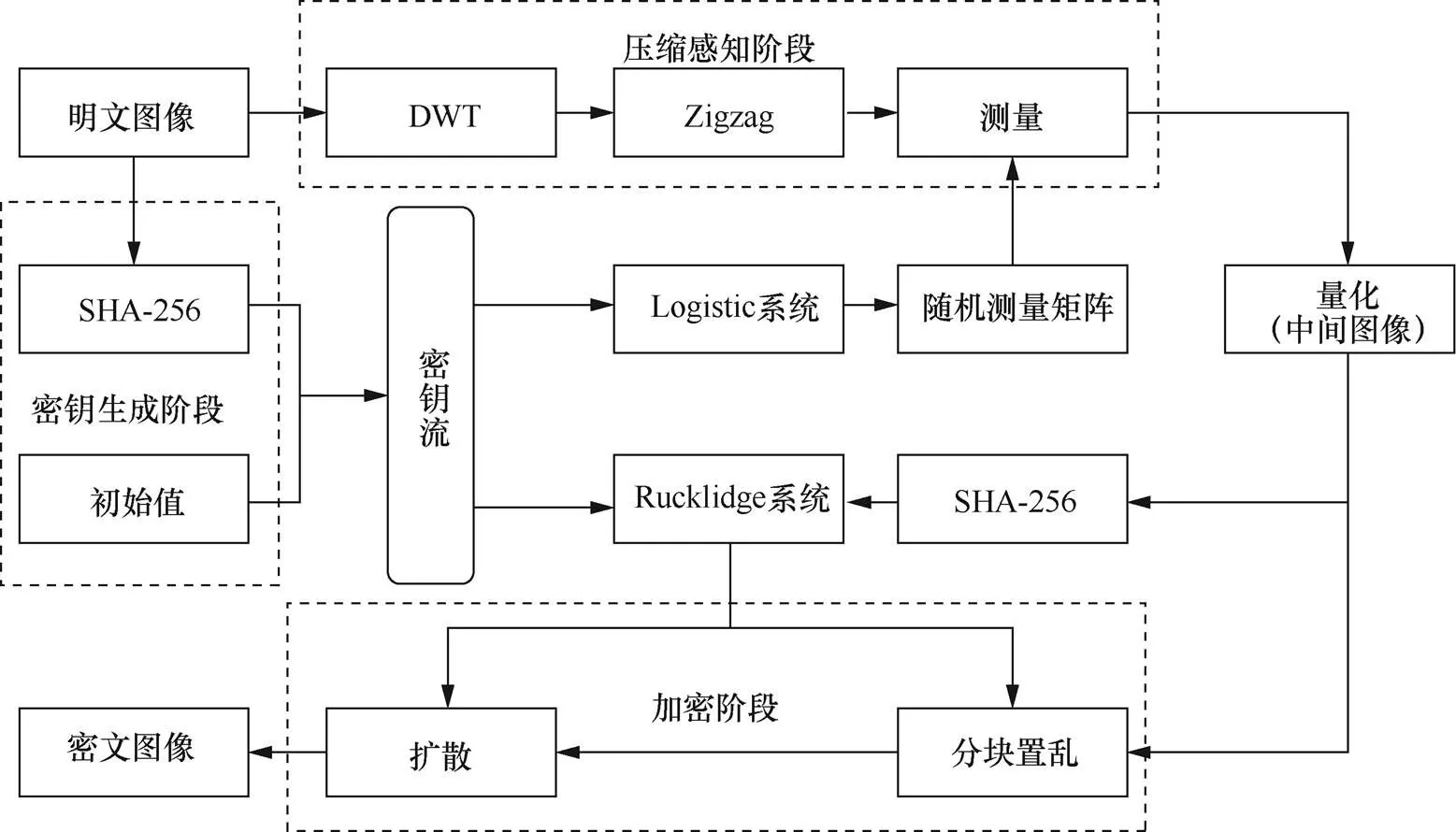
图1 图像加密流程

Figure 1 Flow chart of image encryption

4) 对稀疏系数矩阵1使用Zigzag置乱，得到2。

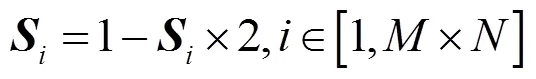
7) 使用式(8)将3量化到[0～255]范围，得到中间图像4，式中max和min分别为3的最大值和最小值。

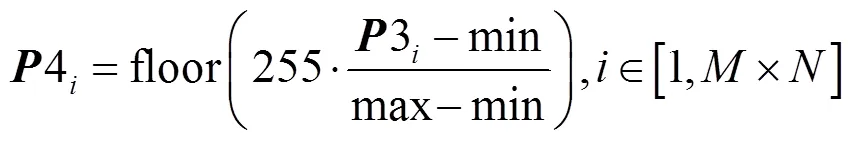
8) 计算中间图像4的SHA-256哈希值得到序列KA、和KA使用式(5)得到KB，使用KB和式(6)得到Rucklidge混沌系统初始值rx0、ry0、rz0，并生成长度为1 000+的4条混沌序列1234，为避免瞬态效应，均舍弃前1 000项值。

9) 将长度为的随机序列1拆分为两个长度为2的随机序列，并将其按列优先方式重塑为两个行2列的随机矩阵、，同理，拆分2为两个行2列的随机矩阵、，使用4个随机矩阵和2.1节描述的置乱算法，对4进行置乱操作，得到5。

10) 分别使用3、4作为扩散算法的正向扩散和逆向扩散混沌序列，对5使用式(9)、式(11)的扩散算法对图像进一步置乱得到6，即最终的秘密图像。

本文采用的扩散算法是与明文相关联的双向加取模运算，该算法简单且可以很好地将像素值扩散到尽可能多的像素点。公式描述如下。

正向扩散如下：

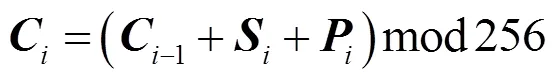
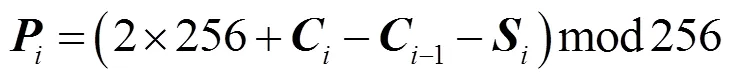
逆向扩散如下：

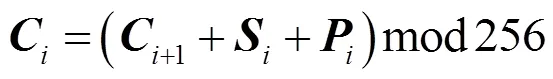
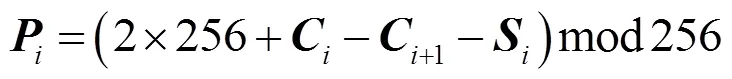
其中，为给定的待扩散明文图像，为给定的控制扩散的混沌序列，为扩散后的密文图像。式(9)、式(10)分别是正向扩散算法和与之对应的还原算法。式(11)、式(12)分别是逆向扩散算法和相应的还原算法。

2.2.3 解密过程

解密过程是加密过程的逆过程，其流程如图2所示，其过程简述如下。

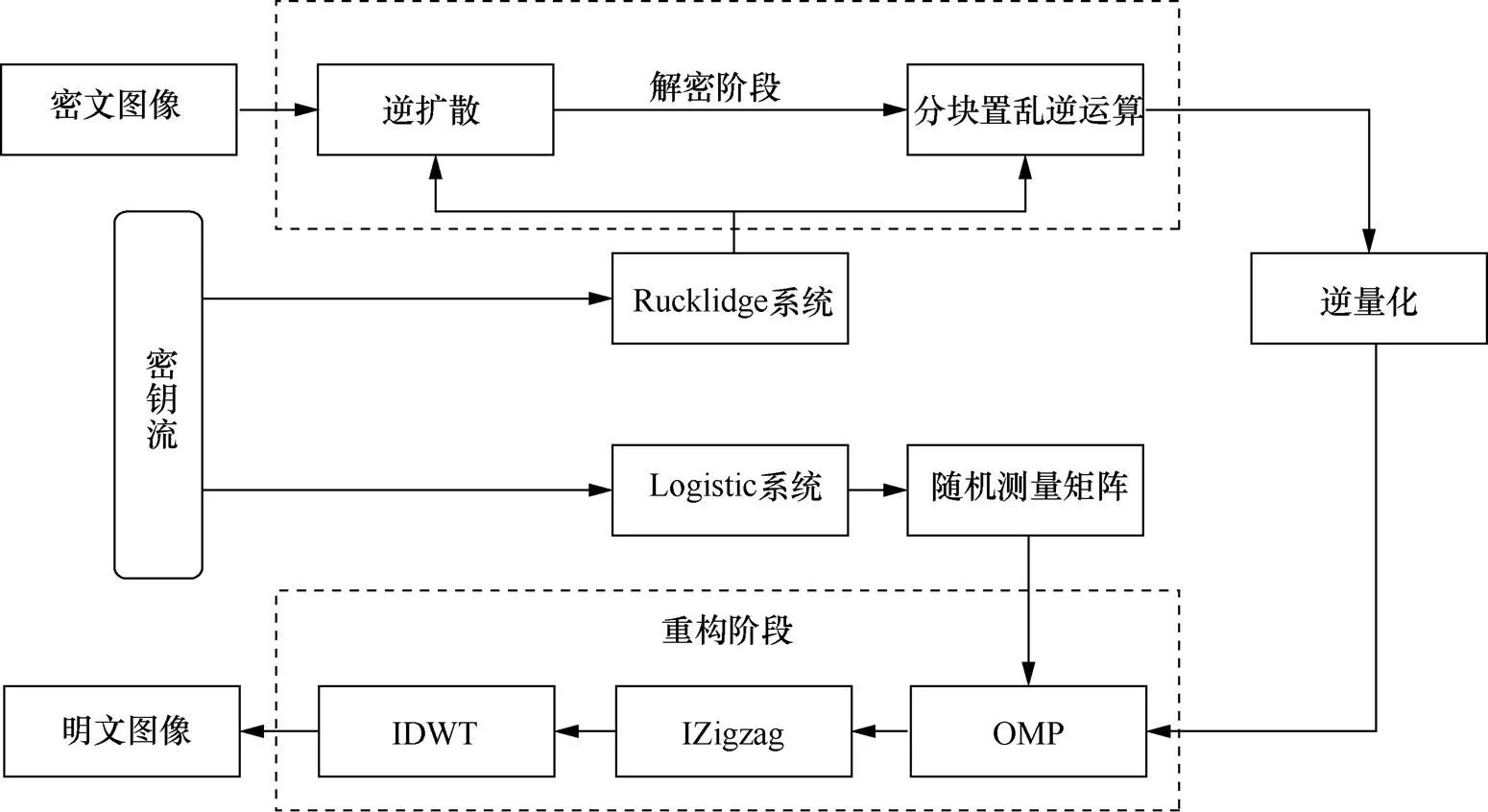
图2 图像解密算法流程

Figure 2 Flow chart of image decryption algorithm

3) 结合3和4对6使用式(10)、式(12)进行扩散的还原操作，得到5。

4) 使用1和2生成4个随机矩阵、、、，并使用置乱算法逆运算将5还原为4。

5) 使用式(13)将图像4进行逆量化，得到3。

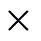
7) 对2进行Zigzag逆变换得到1。

8) 对1使用离散小波逆变换，得到明文图像。

3 实验仿真及其安全性能分析

3.1 仿真实验

图3 明文测试图像

Figure 3 Plain test image

图4 Lena加解密结果

Figure 4 Lena encryption and decryption results

仿真结果显示，经过加密后的密文图像杂乱无章，并且按照压缩比缩放，所重构的图像与原图像基本一致，表明本文算法能同时完成图像的压缩和加密，图像的重构质量良好。

3.2 直方图分析

直方图表示的是图像中每个灰度值出现的频率，是像素值分布的规律。一个良好的密文图像，其频率直方图应是水平的。图像及其直方图如图7所示。

图5 Cameraman加解密结果

Figure 5 Cameraman encryption and decryption results

图6 House加解密结果

Figure 6 House encryption and decryption results

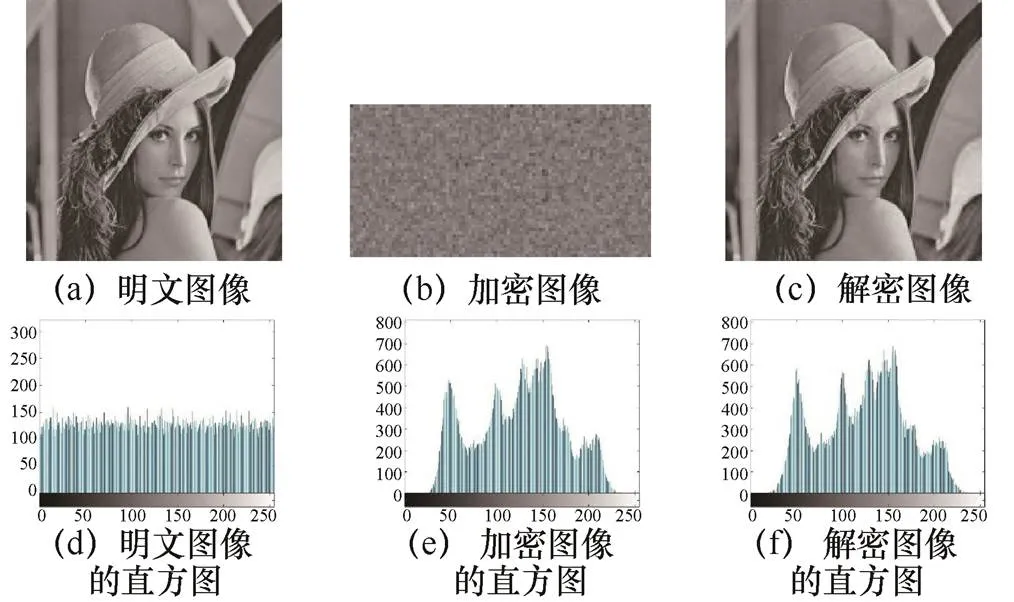
图7 图像及其直方图

Figure 7 Image and its histogram

图7表明密文图像的直方图是水平的，说明本文算法能很好地抵抗灰度统计攻击，且明文图像和重构图像的直方图分布基本一致，说明本算法很好地还原了明文图像。

3.3 相关性分析

一般明文图像在水平方向、垂直方向和对角线方向相邻像素点之间具有高度的相关性。因此图像加密算法应该能够完全打破各个方向的相邻像素间的相关性。计算相关性的公式如下：

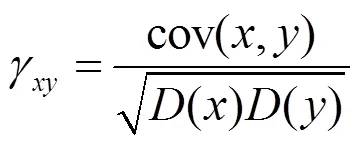
对Lena图像的相关性分析如图8所示。明文图像的像素点集中地分布在一起，而密文图像无论是从水平方向、竖直方向和对角线方向上看，像素点都均匀地分布在图像的各个区域。表1分别给出了10幅图像的明文图像和密文图像的相关系数，表2给出了表1数据的均值与其他文献的对比结果。

分析表1可得，密文图像在3个方向上相关性都接近于0，且通过表2与其他方案的对比，可看出本文算法略优于其他文献提出的算法。

3.4 密钥敏感性分析

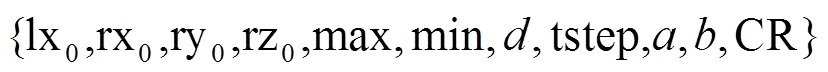
图9给出了密钥敏感性测试结果，分别分析了lx0、rx0、ry0、rz0共4个混沌系统初始值密钥敏感性和Rucklidge混沌系统步长tstep的密钥敏感性。这里令每个密钥值增加10−15，然后解密密文图像。分析仿真测试，本算法具有较好的密钥敏感性，且密钥空间理论上达到2349>>2100。

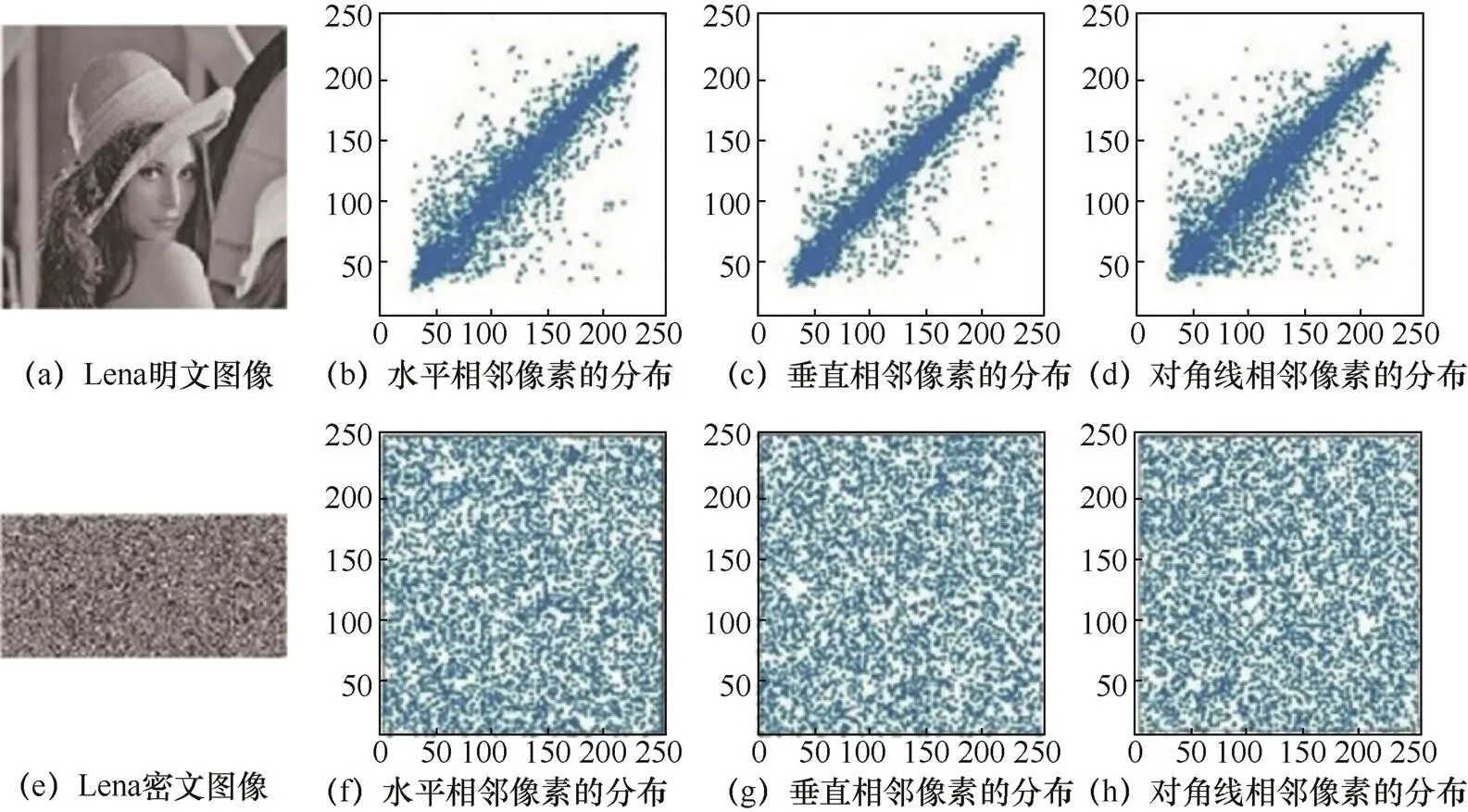
图8 对Lena图像的相关分析

Figure 8 Correlation analysis of Lena images

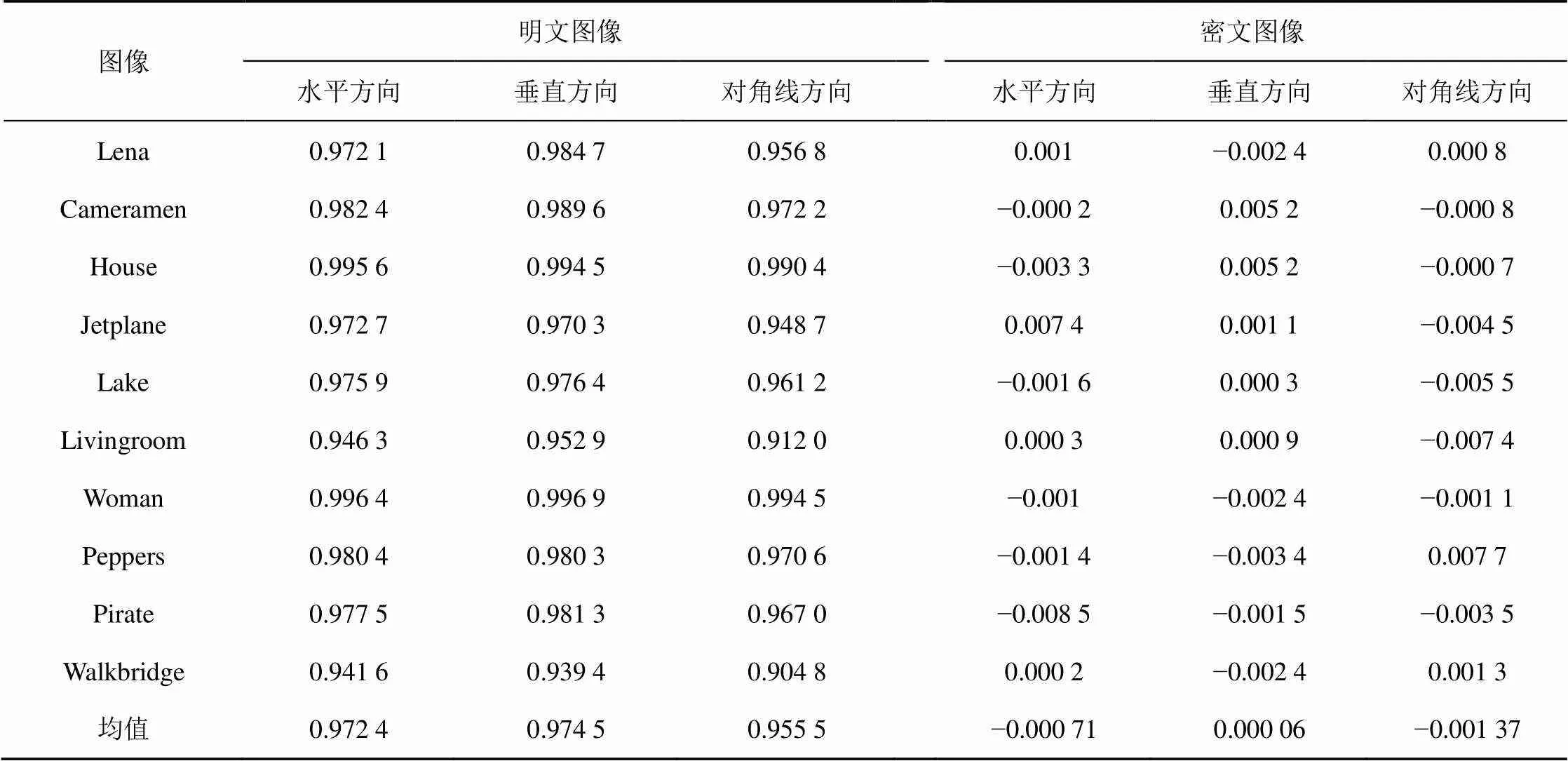
表1 明文图像和密文图像不同方向上相邻像素的相关系数

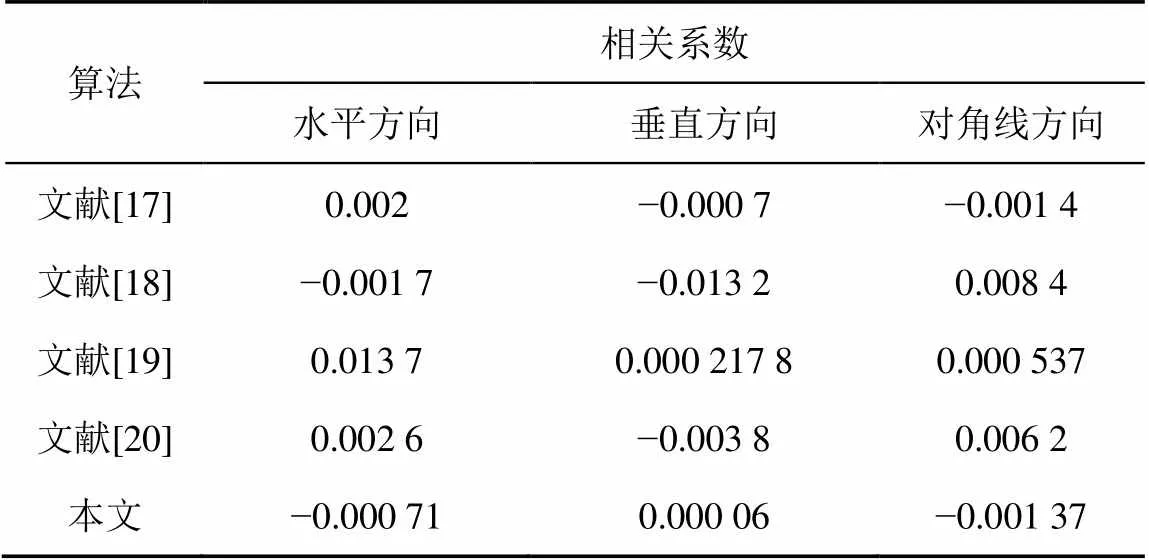
表2 不同算法相关系数均值比较

图9 密钥敏感性测试

Figure 9 Key sensitivity test

3.5 信息熵分析

信息熵用来评估图像的随机性。图像的信息越随机，信息熵越大。信息熵的计算公式如下：

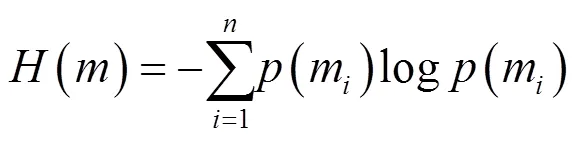
其中，是像素值集合，(m)为像素值出现的概率，为集合的大小。对于一个256×256灰度图像而言，信息熵的理想值是8。表3分别给出了5幅明文图像和密文图像的信息熵值，表4给出了5幅密文图像信息熵均值和其他文献对比结果。

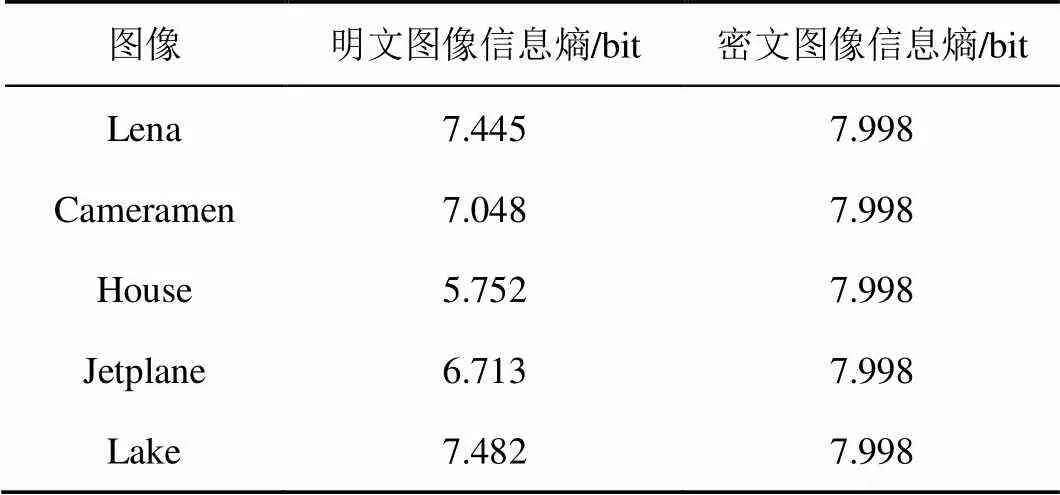
表3 明文图像与密文图像的信息熵

表4 不同算法信息熵均值比较

从表3和表4可看出，每幅密文图像的信息熵值都接近于理想值8，且本文的信息熵略微优于表4给出的对比文献，表明本文算法生成的密文图像有着良好的随机性。

3.6 峰值信噪比分析

峰值信噪比（PSNR，peak signal to noise ratio）是描述图像失真或噪声水平的指标，通常用来评估信号重构效果，其定义如下：

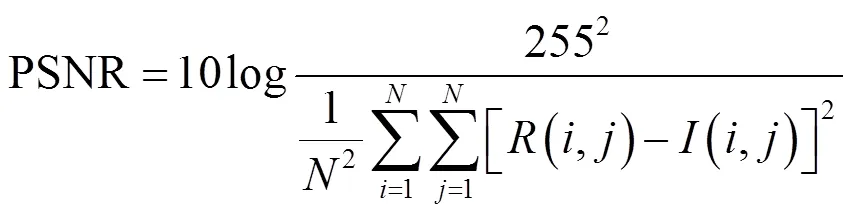
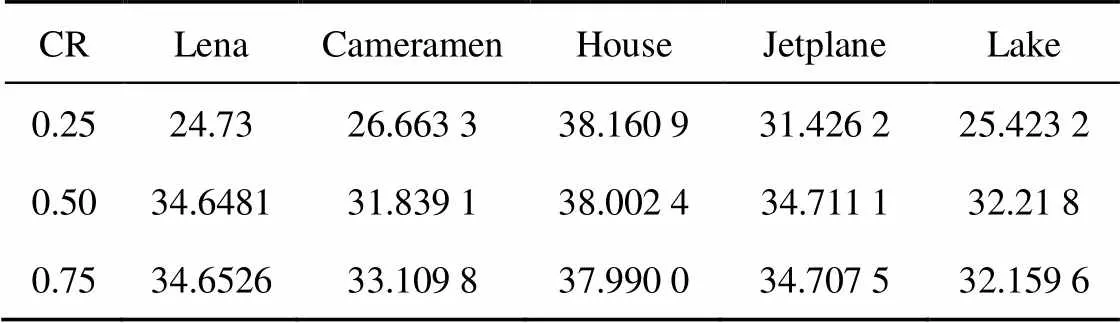
表5 不同图像的PSNR

分析表5和上文仿真结果图像可知，解密后的图像质量良好，最高PSNR值为38.160 9 dB，即使压缩比为CR=0.25，重构图像的质量也可以接受。实验表明本文算法的重构效果良好。

3.7 抗差分攻击分析

攻击者常常会对明文图像轻微更改像素值，然后分析密文图像变化情况。因此，一个良好的图像加密算法在明文发生微小的变化后，密文应该有很大变化。像素变化率（NPCR，the number of pixels change rate）和统一平均变化强度（UACI，the unified average changing intensity）经常被用来评估像素是否能够抵抗差分攻击。NPCR和UACI的计算公式分别如下：

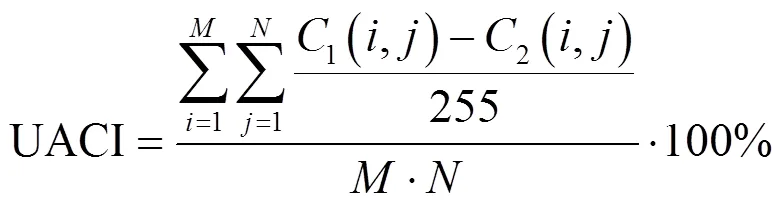
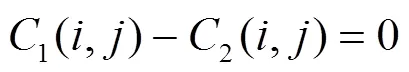
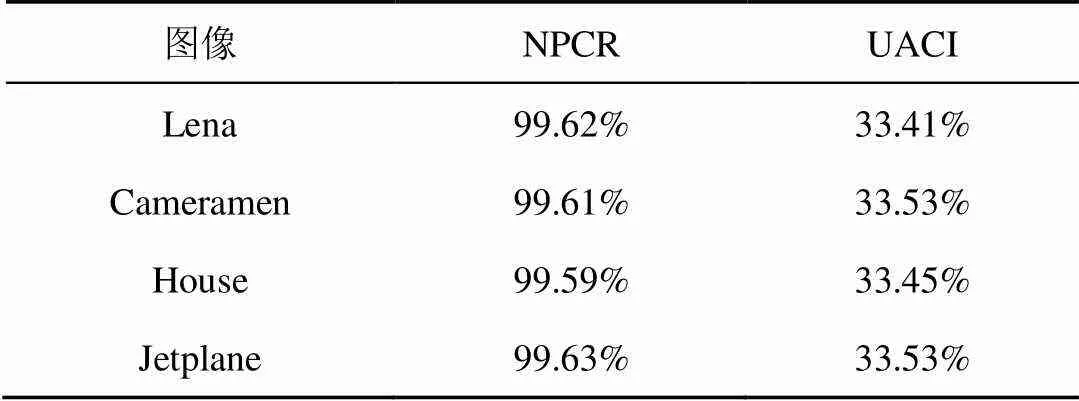
表6 NPCR与UACI值

表7 不同算法 NPCR 和 UACI均值比较

在理想状态下，NPCR和UACI的理想值为99.609 4%和33.463 5%。从表6和表7中可看出所例算法的仿真结果都能够满足要求，表明本文算法对明文图像变化高度敏感，有着良好的抗差分攻击特性。

3.8 时间复杂性分析

图像的加解密时间是衡量一个算法性能的重要指标。表8是本文算法在CR0.5时使用不同明文图像计算的加解密时间。表9给出了本算法使用Lena图像的加解密时间和其他文献的对比结果。

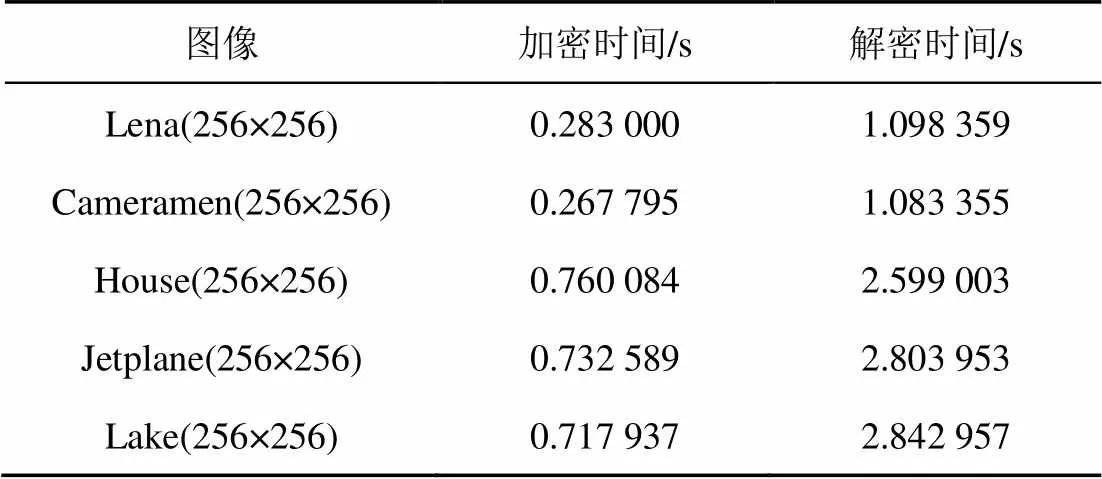
表8 不同图像的加解密时间，CR=0.5

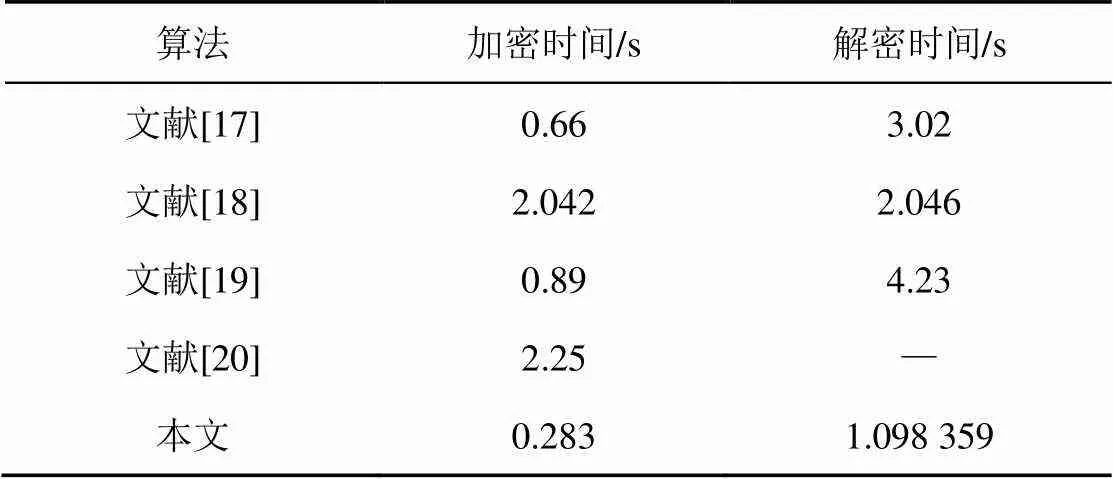
表9 本文算法与其他算法加密和解密时间的比较结果，CR=0.5

从表8和表9可看出，本文算法分别在图像大小为256×256和512×512时都有着良好的加解密速度，且本文算法的加解密时间均优于表中的对比文献，具有较好的加解密性能。

4 结束语

本文提出了一种新的基于双混沌系统和CS的图像加密算法，该算法使用明文图像和中间图像的哈希值构造密钥流，提出一种新的与明文关联的分块置乱算法，可更好地抵抗选择明文攻击和差分攻击。在对图像CS后，又进行了二次加密，弥补了CS线性测量的缺陷。仿真实验和性能分析表明本文算法有着较好的重构质量，能够有效抵抗各种攻击，并且具有良好的加密性能。与其他算法对比，本文算法在加密性能和重构质量上有着更好的实用性和可靠性。

[1] KAUR M, SINGH S, KAUR M, et al. A systematic review of metaheuristic-based image encryption techniques[J]. Archives of Computational Methods in Engineering, 2022, 29(5): 2563-257.

[2] CANDES E J, TAO T. Near-optimal signal recovery from random projections: Universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.

[3] ORSDEMIR A, ALTUN H O, SHARMA G, et al. On the security and robustness of encryption via compressed sensing[C]//MILCOM 2008 IEEE Military Communications Conference. 2008: 1-7.

[4] XU Q, SUN K, CAO C, et al. A fast image encryption algorithm based on compressive sensing and hyperchaotic map[J]. Optics and Lasers in Engineering, 2019, 12(10): 203-214.

[5] YE G, PAN C, DONG Y, et al. Image encryption and hiding algorithm based on compressive sensing and random numbers insertion[J]. Signal Processing, 2020, 172: 107563.

[6] XU Q, SUN K, HE S, et al. An effective image encryption algorithm based on compressive sensing and 2D-SLIM[J]. Optics and Lasers in Engineering, 2020, 134: 106178.

[7] WANG X, LIU C, JIANG D. A novel triple-image encryption and hiding algorithm based on chaos, compressive sensing and 3D DCT[J]. Information Sciences, 2021, 574: 505-527.

[8] LI L, FANG Y, LIU L, et al. Overview of compressed sensing: sensing model, reconstruction algorithm, and its applications[J]. Applied Sciences, 2020, 10(17): 5909.

[9] AHMID M, KAZAR O. A comprehensive review of the internet of things security[J]. Journal of Applied Security Research, 2021, 5(4): 1-17.

[10] LIU Y, ZHANG L Y, WANG J, et al. Chosen-plaintext attack of an image encryption scheme based on modified permutation–diffusion structure[J]. Nonlinear Dynamics, 2016, 84(4): 2241-2250.

[11] CIVINO R, BLONDEAU C, SALA M. Differential attacks: using alternative operations[J]. Designs, Codes and Cryptography, 2019, 87(2): 225-247.

[12] KSHEERASAGAR T K, ANURADHA S, AVADHOOTHA G, et al. Performance analysis of DS-CDMA using different chaotic sequences[C]//2016 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET). 2016: 2421-2425.

[13] GONG L H, LUO H X, WU R Q, et al. New 4D chaotic system with hidden attractors and self-excited attractors and its application in image encryption based on RNG[J]. Physica A: Statistical Mechanics and its Applications, 2022, 591: 126793.

[14] LIU E, TEMLYAKOV V N. The orthogonal super greedy algorithm and applications in compressed sensing[J]. IEEE Transactions on Information Theory, 2011, 58(4): 2040-2047.

[15] MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.

[16] MOHIMANI H, BABAIE-ZADEH M, JUTTEN C. A fast approach for overcomplete sparse decomposition based on smoothed0norm[J]. IEEE Transactions on Signal Processing, 2008, 57(1): 289-301.

[17] WANG X Y, ZHANG Y Q, BAO X M. A novel chaotic image encryption scheme using DNA sequence operations[J]. Optics and Lasers in Engineering, 2015, 73: 53-61.

[18] WANG X, CHEN S, ZHANG Y. A chaotic image encryption algorithm based on random dynamic mixing[J]. Optics & Laser Technology, 2021, 138: 106837.

[19] CHAI X L, GAN Z H, YUAN K, et al. An image encryption scheme based on three-dimensional Brownian motion and chaotic system[J]. Chinese Physics B, 2017, 26(2): 020504.

[20] AHMAD J, HWANG S O. A secure image encryption scheme based on chaotic maps and affine transformation[J]. Multimedia Tools and Applications, 2016, 75(21): 13951-13976.

New image encryption algorithm based on double chaotic system and compressive sensing

YANG Yuguang, CAO Guodong

Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China

Image encryption technology plays an important role in today’s multimedia applications and Internet information security transmission. However, most image encryption algorithms still have problems, for example, cipher images occupied high bandwidth during transmission, image encryption speed is slow, image encryption algorithms are not associated with plain image, and there is no complete ciphertext feedback mechanism. These problems all affect the security and easy use of image encryption algorithms. In order to solve the above problems, the compressive sensing technology and chaotic system were studied, and a new image encryption algorithm based on double chaotic system and compressive sensing with plaintext association was proposed. The plaintext image association key was used to associate the plain image hash value with the Logistic chaotic system parameters. Discrete wavelet transform, was used to sparse the plain image. Then the random measurement matrix was generated by the Logistic chaos system, and the image was encrypted once by combining the compressive sensing technique and the random measurement matrix to obtain the intermediate image. The intermediate image was hashed again, and the Rucklidge chaos system initial value was associated with the plain image hash value together. The Rucklidge chaotic system and encryption algorithm were used to control the intermediate image for secondary encryption and accordingly obtain the cipher image. The encryption algorithm was a new plaintext correlation encryption algorithm, which used the image’s own pixel value to control the scrambling of the intermediate image. It also enhanced the plaintext association and established a ciphertext feedback mechanism. Simulation results and performance analysis show that the algorithm has good encryption performance. The encrypted image can be compressed according to the compression ratio, effectively reducing the size of the cipher image. Moreover, it is resistant to common attacks such as known plaintext attack, selective plaintext attack and differential attack, which is better than other common image encryption algorithms.

image encryption, compressive sensing, double chaotic system, plaintext association, discrete wavelet transform

TP309

A

10.11959/j.issn.2096−109x.2022058

2022−01−20；

2022−05−12

杨宇光，yangyang7357@bjut.edu.cn

国家自然科学基金（62071015）

The National Natural Science Foundation of China (62071015)

杨宇光, 曹国栋. 新的基于双混沌系统和压缩感知的图像加密算法[J]. 网络与信息安全学报, 2022, 8(5): 88-97.

Format: YANG Y G, CAO G D. New image encryption algorithm based on double chaotic system and compressive sensing[J]. Chinese Journal of Network and Information Security, 2022, 8(5): 88-97.

杨宇光（1976−），女，河北衡水人，北京工业大学教授、博士生导师，主要研究方向为信息安全。

曹国栋（1997−），男，山东菏泽人，北京工业大学硕士生，主要研究方向为信息安全。