基于Sage-Husa EKF算法的锂离子电池能量状态估计

李晓涵，孙 磊，马 勇，郭东亮，肖 鹏，刘建军，吴 鹏，张志行，韩雪冰

（1国网江苏省电力有限公司电力科学研究院，江苏 南京 211103；2清华大学车辆与运载学院，北京 100084）

锂离子电池工作时内部发生复杂的物理化学反应，其可用能量状态同时受到充放电电压、电流、环境及工作温度等因素的影响，因此建立能够准确预测电池端电压变化的模型，应用合适的能量状态(state of energy，SOE)估计算法预测电池的能量状态，能够有效提升电池系统的工作性能[1-5]。

针对锂离子电池的SOE 估计，很多研究者提出了不同的估计算法和策略。文献[6]使用改进的功率积分法对电池的SOE 定义并进行估计，该方法测量中引入的噪声和计算迭代估计误差会持续累积，导致SOE的估计结果呈现发散趋势。文献[7]建立了单一温度下的锂离子电池模型，并结合滤波算法对电池的SOE 进行估计，算法具有较好的鲁棒性，但是其并没有考虑不同温度下电池模型参数的变化，导致模型的适用度降低。文献[8]使用改进的戴维南模型，利用扩展卡尔曼滤波(extended Kalman filter，EKF)算法估计电池在动态工况下的SOE 值，但是其没有考虑非高斯分布下的过程噪声和量测噪声对EKF算法的影响，导致算法精度较低。文献[9]将神经网络法应用于SOE 的估计，具有较好的预测精度，但是其预测精度的进一步提高受到输入的实验数据质量和数量制约。文献[10]在电池当前状态估计基础之上，对电池未来充放电过程中的关键参变量进行耦合预测，提出了一种基于预测-自适应的电池能量状态估计方法，但是该方法的计算过程较为繁杂。因此，精确的SOE 估计需要结合有限的电流和电压数据，考虑计算的复杂度，建立合适的等效电路模型，辨识得到不同温度下的模型参数，提高模型的适用性，并进一步考虑过程噪声对算法的影响，提高算法的精度[11-13]。

本工作使用Sage-Husa 自适应扩展卡尔曼滤波(Sage-Husa extended Kalman filter，S-H EKF)算法对锂离子电池能量状态进行估计。S-H EKF算法对过程协方差矩阵进行迭代更新，在非高斯分布的随机噪声下，能够提高SOE 估计的精度和鲁棒性。首先，本工作针对磷酸铁锂电池展开研究，分析其工作特性，得到电池能量与温度的函数关系。之后，考虑参数值随温度和SOE 值变化，建立二阶RC 等效电路模型，利用该模型对电池的端电压进行预测。最后，结合动态工况和间歇大倍率充电工况实验结果，选取适用于非线性系统的SOE 估计算法预测电池的能量状态。通过对比分析，S-H EKF 算法比EKF 的SOE 估计精度更高，更加适用于锂离子电池的SOE估计。

1 电池性能实验

深入了解电池的工作特性，有助于建立准确的电池模型，模拟电池充放电路径，增强SOE 估计的准确性。电池在不同的环境温度下所能放出的能量是不同的，因此需要对电池的能量特性进行分析[14-15]。电池的实验平台如图1 所示，充放电测试仪最大测试电压为5 V，最大测试电流为200 A，充放电测试仪通过CAN通讯线与数据采集仪连接，传输电池的实验电压和电流数据，电池置于温箱中，温箱提供恒定的温度环境，其可调温度范围为-40～150 ℃。

图1 电池实验平台Fig.1 Battery test platform

本工作研究的对象为ΙFP1865140 动力型方壳磷酸铁锂电池，其基本参数如表1所示。

表1 LiFePO4电池基本参数Table 1 LiFePO4 cell basic parameters

对上述电池在45 ℃、25 ℃、10 ℃、0 ℃、-10 ℃、-20 ℃这6个温度点下进行标准容量/能量实验。标准容量/能量实验的目的是获取特定温度节点下电池容量和能量的基准参照值。

标准容量/能量实验的方法为：

（1）在特定温度节点下静置，让电池适应环境温度。

（2）以12.5 A的电流恒流恒压充电，截止电流为0.25 A。

（3）静置。

（4）以12.5 A的电流放电到下截止电压2 V。

（5）重复步骤(2)～(4)三次。

标准容量/能量实验中的3次放电平均容量记为C0，放电平均能量记为W0，以C0和W0作为该温度节点下的标准容量和能量。45 ℃下的实验结果如图2所示，不同温度下所能放出的标准容量C0和标准能量W0如表2所示。

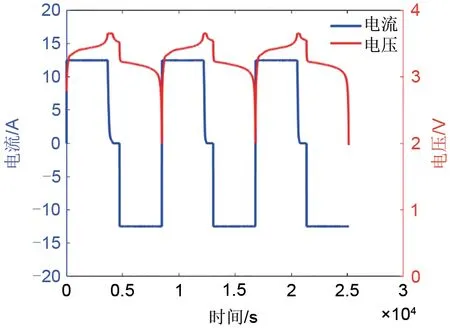
图2 45 ℃标准容量/能量实验Fig.2 45 ℃standard capacity/energy test

由表2可以分析出，电池放出的能量和容量随着温度的降低而降低，温度对电池的可放能量影响较大。主要原因为：温度越低，电池内部化学材料的活性就越低，表现为电池的内阻增大，放电开始和结束电压降幅增大，且放电平台电压降低，稳定的放电持续时间变短，导致电池的可用能量降低。具体来说，电池在放电的过程中，锂离子在正负极固相颗粒中扩散，并在电解液中迁移，其运动规律分别满足Fick 第一定律和Nernst-Planck 方程，如公式(1)和公式(2)所示。

表2 不同温度下电池的标准容量/能量Table 2 Standard capacity/energy of batteries at different temperatures

式中，J为扩散通量；D为扩散系数；c为锂离子的体积浓度；F为法拉第常数；R为气体常数；T为温度；φ为电极的电势；x为锂离子的位置坐标。

由上述公式可知，当温度T降低时，扩散系数D减小，电极的反应电流密度下降，整体反映为电池放出标准能量的降低，本工作将标准能量与温度用4次多项式进行拟合，拟合结果如公式(3)和图3所示。

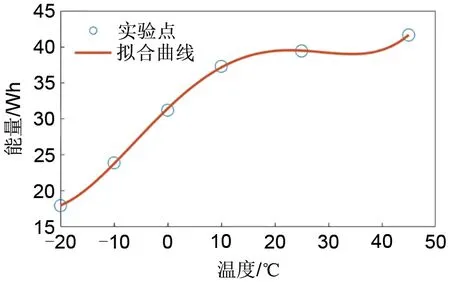
图3 电池在不同温度下的标准能量拟合Fig.3 Standard energy fitting of batteries at different temperatures

式中，W(T)为不同温度下电池的标准能量；T为温度。

2 电池模型建立及验证

2.1 二阶RC等效电路模型建立

磷酸铁锂电池的端电压U是最为重要的外特性参数。如图2所示，在电池充放电的过程中，端电压不是一个常数值，在放电初期和放电末期电压快速下降，与电池的能量状态有着密切的非线性关系。因此，需要建立电池的端电压模型进行端电压的实时预测，为后续SOE 的估计提供准确的输入参数。

如图4 所示，考虑参数值随温度和SOE 的变化，建立二阶RC 等效电路模型，来模拟锂离子电池在电流激励下的端电压响应特性。该模型包含两个RC 环节，流经电阻的电流为法拉第电流，流经电容的电流为非法拉第电流，两个RC 环节分别模拟电池充放电过程中的浓差极化和电化学极化，两种极化会导致电压弛豫现象，用电阻来近似电池的欧姆极化导致的瞬时压降。

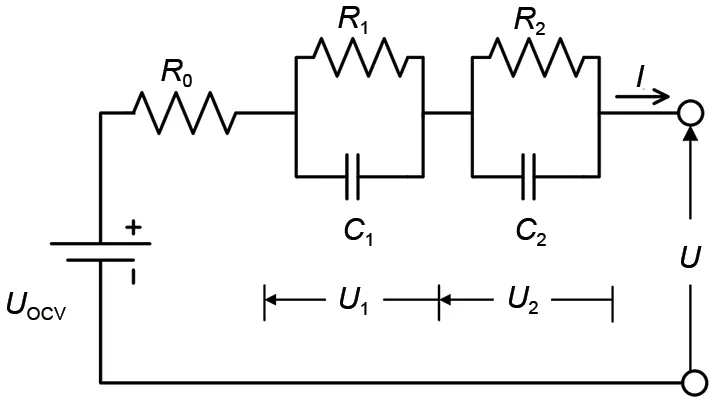
图4 二阶RC等效电路模型Fig.4 Second-order RC equivalent circuit model

根据基尔霍夫定律，列出二阶RC等效电路模型的状态方程和输出方程，如公式(4)、(5)和(6)所示。

状态方程：

式中，UOCV为电池在没有电流流过时充分静置下的开路电压值；R0、R1和R2分别为欧姆内阻、电化学极化和浓差极化内阻；C1和C2分别为电化学和浓差极化电容；U1为第一个RC回路两端的电压值；U2为第二个RC 回路两端的电压值；U为电池的端电压。

2.2 模型参数辨识

二阶RC 模型中需要辨识的参数包括欧姆内阻R0，极化内阻R1和R2，极化电容C1和C2和两个RC 回路的时间常数τ1和τ2。模型参数辨识采用HPPC(hybrid pulse power characteristic)实验。HPPC是美国电动汽车动力电池检测手册中推荐的复合脉冲功率特性工况实验，可以根据电池的电压响应曲线确定电池内阻。HPPC 实验的步骤如下：

（1）在特定温度节点下静置，让电池适应环境温度。（2）以1C0大小的电流恒流恒压将电池充满。（3）用1C0电流放电，放出标准容量10%的电量。

（4）静置1 h。

（5）进行脉冲实验，先以恒定的5C0脉冲电流进行放电10 s，静置40 s，再以恒定的5C0脉冲电流充电10 s。

（6）重复步骤(3)～(5)，直到90%放电深度(depth of discharge，DOD)处进行最后的脉冲实验。

（7）将电池放电至100%DOD。

（8）静置1 h。

45 ℃的HPPC实验结果如图5所示。

图5 45 ℃HPPC实验结果Fig.5 Results of HPPC experiment at 45 ℃

如图6 所示，图中的电流电压曲线为电池HPPC实验过程中脉冲电压响应局部放大图，以该图为例说明模型参数的辨识方法。

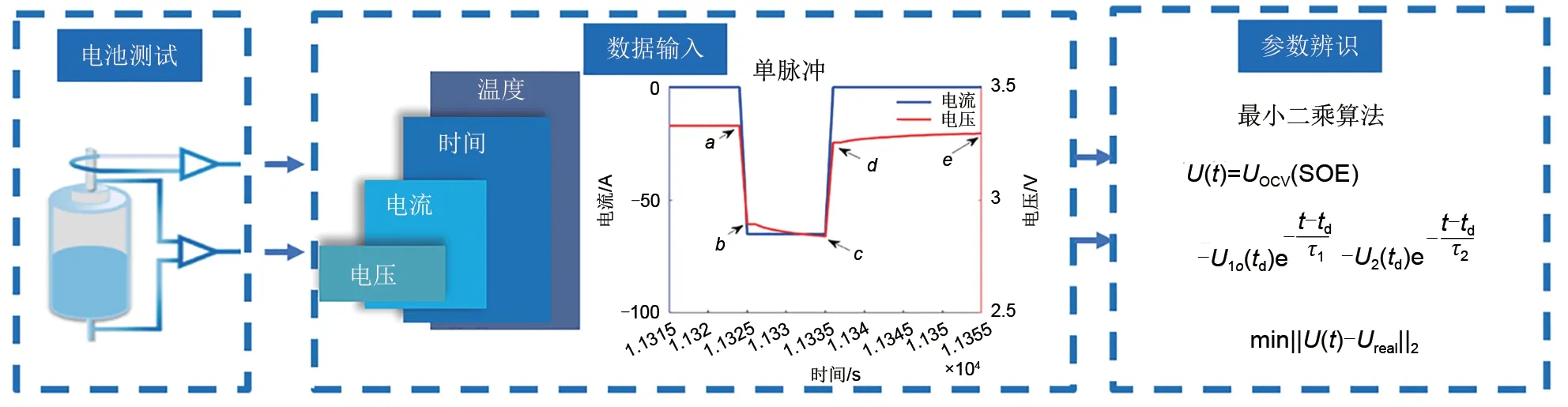
图6 参数辨识示意图Fig.6 Schematic diagram of parameter identification

首先，a～b的瞬时电压下降和c～d的瞬时电压上升是由欧姆内阻R0造成，因此

在d～e阶段，电流激励I=0，RC 回路为零输入状态。

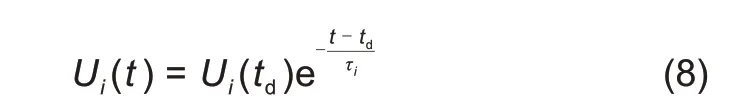
其中，Ui(td)为td时刻第i个RC 回路端电压；τi为第i个RC回路的时间常数，i=1,2。

此时电路的端电压响应为：

UOCV为静置末端e处的电压，通过最小二乘法拟合，可以得到参数Ui(td)、τ1和τ2的值。

图6 中a为电池脉冲后长时间静置的末端，可以假定此时内部的极化作用完全消失。Ub至Uc阶段为RC电路的零状态响应。

其中，Ri表示第i个RC回路的极化内阻，i=1,2。

RC回路的时间常数由以下公式计算得到。

对上文给定的锂离子电池在45 ℃、25 ℃、10 ℃、0 ℃、-10 ℃和-20 ℃6个温度节点下进行HPPC实验，欧姆内阻R0、极化内阻R1、R2、极化电容C1、C2参数辨识结果如图7(a)～(e)所示。

图7 参数辨识结果Fig.7 Parameter identification results

2.3 模型验证

模型建立完成后，对模型的端电压仿真精度还需进一步验证，将上述辨识得到的参数代入到二阶RC 等效电路模型中，得到端电压仿真值。45 ℃、25 ℃、-20 ℃HPPC实验的端电压仿真值和真实值的对比和误差分析如图8和表3所示。

表3 端电压电压误差结果分析Table 3 Terminal voltage error analysis

从图8可以分析出，所建立的模型能够较好地仿真电池充放电过程中的端电压变化。端电压仿真误差主要来源于脉冲充放电阶段，此时电池内部的反应情况更为复杂，放电末端电池内部极化作用明显，材料的活性降低，电池特性发生明显变化。通过误差分析，可以得到常温和高温下电压仿真的均方根误差均小于18 mV，低温下电池的包括欧姆极化、浓差极化和电化学极化在内的极化特征更为明显，导致低温下的模型误差均值有所增加，但仍小于27 mV，能够满足SOE估计的精度要求。

图8 45 ℃、25 ℃、-20 ℃HPPC实验模型端电压验证Fig.8 Terminal voltage validation of HPPC experimental models at 45 ℃,25 ℃and-20 ℃

3 基于Sage-Husa EKF 算法的SOE估计

SOE 表示电池某时刻下的能量状态，定义为电池的剩余能量与标准能量的比值，其取值范围为0～1。放出的能量为电压与电流的乘积积分，根据上述分析，标准能量与温度有关，确定SOE 的表达式如式(12)所示。

式中：zK为电池k时间步SOE 状态值；z0为SOE 状态初始值；U为电池的端电压值；W(T)为电池在不同温度下的标准能量；η为库仑效率，一般取为1。

公式(12)的关键在于端电压与电流的乘积与电池能量比值的计算，而电池能量与温度和电池端电压与SOE之间均是非线性关系。考虑前述第一部分建立了电池能量与温度之间的关系，第二部分建立了不同温度下的电池端电压模型，进一步考虑公式(4)、(5)、(6)和(12)，将二阶RC 等效电路模型和SOE估计公式建立状态方程，并离散化，可以表示为：

其中Uk和Uk+1表示k时间步和k+1 时间步电池的端电压值；U1，k+1和U2，k+1表示两个RC 回路两端k+1 时间步的电压；U1，k和U2，k表示两个RC 回路两端k时间步的电压；zk+1和zk分别为电池k+1时间步和k时间步的SOE 值；∆t为系统的采样时间间隔；R0为欧姆内阻；R1和R2为电化学极化和浓差极化内阻；C1和C2为电化学极化电容和浓差极化电容；W(T)为电池在一定温度下的标准能量；Ik和Ik+1为k时间步和k+1 时间步的电流值；UOCV为开路电压值。

进一步地，电池的非线性系统的状态方程可以表示为

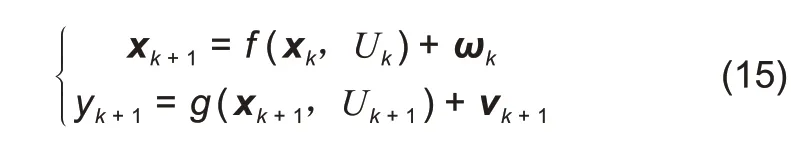
其中xk+1=[U1,k+1U2,k+1zk+1]T为系统的状态变量；Uk=Ik，yk+1为观测值，是电池的端电压；ωk为系统的过程噪声；vk+1为系统的观测噪声，假定过程噪声和观测噪声为相互独立且满足正态分布的高斯白噪声。

对式(15)进行泰勒级数一阶截断展开：

Hk为电池观测空间方程对状态向量求偏导的雅可比矩阵。

EKF算法规定，过程噪声和测量噪声的统计特性为相互独立的高斯分布[16-19]，而电池的真实工作状态并非如此，电流电压传感器的噪声通常是未知的和随机的，这可能会导致EKF算法的估计误差增大，甚至造成算法的发散。

本工作利用S-H EKF算法迭代更新过程噪声协方差进行SOE 的估计，以提高SOE 估计的准确性。S-H EKF 算法是在EKF 算法的基础上，引入遗忘迭代因子实时更新噪声的变化，通过极大后验估计实现滤波。在S-H EKF算法中使用协方差矩阵的自适应修正项，能够对系统噪声和观测噪声进行实时迭代优化，保证算法滤波的鲁棒性与稳定性，更加适用于离散时变系统的应用[20]。考虑到目前电压传感器精度较高，抗干扰能力较强，在S-H EKF算法中仅对过程噪声协方差矩阵进行迭代更新，以降低算法的复杂度，进一步提高其实车应用的可能性。其自适应迭代修正公式如式(19)～(22)所示。

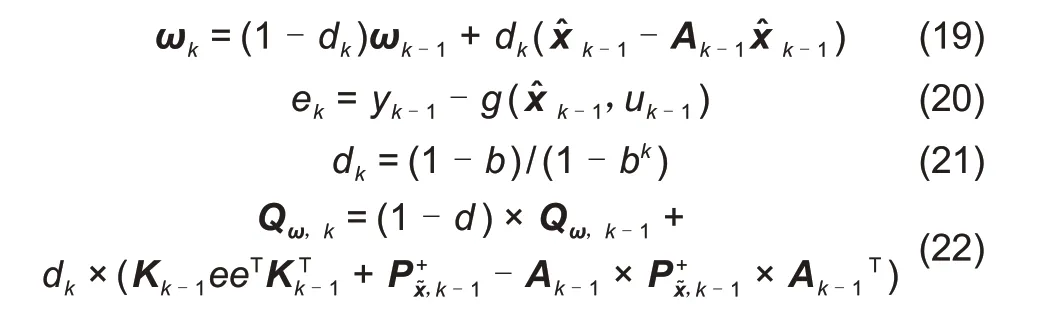
式中，b为Sage-Husa系数，取值范围一般为0.9～1，本工作取0.99；dk为修正因子；ek为第k步的新息误差；Qω,k为第k步的过程噪声协方差矩阵。

Sage-Husa EKF算法流程为：

（1）根据系统k-1 时间步的状态估算系统k时间步的状态，得到状态向量的先验值：

式中，^代表估计值；-代表先验值。

（2）更新协方差矩阵，根据k-1时间步的协方差矩阵得到k时间步误差协方差矩阵的先验值：

（6）误差协方差矩阵测量更新：

式中，I为三维的单位矩阵。

（7）按照公式(19)～(22)对过程噪声协方差矩阵更新。

S-H EKF 估计锂离子电池SOE 的算法步骤如图9所示。

图9 Sage-Husa扩展卡尔曼滤波算法流程Fig.9 Sage-Husa extended Kalman filtering algorithm flow

算法初值设定为：

SOE 估计采用45 ℃、25 ℃、-20 ℃的动态HPPC 测试工况和45 ℃的间歇大倍率充电工况，其中45 ℃的间歇大倍率充电工况电流示意图如图10 所示，以1C0的电流进行充电，每隔10%SOC，进行充电5C0的10 s脉冲，然后以1C0的电流恒流恒压充电至电流小于0.25 A。在该工况下电池的充放电倍率可达到5 C，且充放电时间短，电流方向变化快，脉冲段可以模拟出电池较为恶劣的工作环境。45 ℃、25 ℃、-20 ℃的HPPC工况的SOE 估计结果如图11、图12 和图13 所示，对45 ℃间歇大倍率充电的SOE 估计结果如图14所示，其误差统计分析结果如表4所示。相较于电池的实际应用场景，在实验室环境下，充放电机的电流和电压采集精度较高，且SOE 初值是精确已知的。本工作使用的充放电机电压采集精度为0.005 V，电流采集精度为0.2 A，因此SOE 参考值根据公式(12)计算获得。

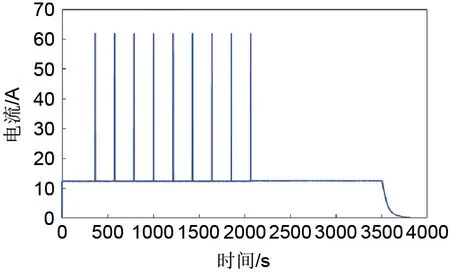
图10 45 ℃间歇大倍率充电电流Fig.10 45 ℃intermittent large multiplier charging current

图11 45 ℃HPPC SOE估计结果Fig.11 45 ℃HPPC SOE estimation results

图12 25 ℃HPPC SOE估计结果Fig.12 25 ℃HPPC SOE estimation results

图13 -20 ℃HPPC SOE估计结果Fig.13 -20 ℃HPPC SOE estimation results

图14 45 ℃间歇大倍率充电充电SOE估计结果Fig.14 Estimated results of intermittent large multiplier charging SOE at 45 ℃

表4 SOE估计误差分析Table 4 SOE estimation error analysis

通过SOE 估计误差分析，在不同的充放电工况下，S-H EKF 相较于EKF 在绝对误差均值、误差最大绝对值和误差均方根三个方面，均表现出更好的精度，且具有更好的误差收敛性，这得益于过程协方差矩阵对非高斯分布的随机噪声自适应迭代修正的效果。在45 ℃、25 ℃、-20 ℃的HPPC工况下和45 ℃间歇大倍率充电工况下，S-H EKF 算法相较于EKF 算法的SOE 估计结果的绝对误差均值的平均值降低20.72%，误差均方根值的平均值相较于EKF算法降低26.93%，因此S-H EKF算法更适合于SOE的估计。

4 结 论

本工作对磷酸铁锂电池的工作特性进行了分析，并基于HPPC实验，使用最小二乘法辨识模型参数，考虑参数值随温度和SOE 的变化，建立了二阶RC 等效电路模型。实验结果表明，模型能够较好地模拟不同温度下电池充放电过程中端电压的变化，且精度较高，能够满足SOE 估计的要求。根据搭建的模型，利用S-H EKF 算法对HPPC 动态工况和45 ℃间歇大倍率充电工况进行电池能量状态估计，并对比两种方法的估计精度。SOE 估计结果显示，以绝对误差均值为对比标准，S-H EKF 的绝对误差均值相较于EKF 算法平均降低20.72%，SOE的估计最大绝对误差小于3%，更加适用于锂离子电池的能量状态估计。