锂离子电池电极微结构的分形建模及热-化耦合

汪振毅，张 赛，胡世旺

（昆明理工大学机电工程学院，云南 昆明 650500）

近年来，由于新能源汽车、电子通信设备等的快速发展，消费者对具有大容量、长寿命、高稳定性和高能量密度的动力锂电池的要求也日渐提高，而电极就是决定上述性能优劣的关键因素，因此科研人员对高能量密度的电极材料做了许多研究[1-3]。在常见车用锂离子电池的组装工艺中，由活性物质粒子与导电剂粒子形成多孔固体骨架，而电解液则填满了里面的孔隙空间，这些多孔电极对锂离子电池的性能具有重要作用[4-5]。在同等情况下，通过测量单颗粒电极所获得的单活性粒子的倍率性能可达几百至一千，而由多个粒子组成电极后其倍率性能降为1～10，由于锂离子电池电极的多孔结构使锂离子在溶液传输中的阻力明显大于在连续液相介质中的传质阻力，因此导致了可达到两个数量级的倍率性能下降[6-9]。

电子传导网络与离子传递网络都深受多孔电极结构参数的影响，因此优化电极的内部结构将成为改善锂离子电池整体综合性能的主要途径[10]。在优化电极结构时，粒径大小及分布、孔隙率和迂曲度是主要的优化参数，而大量试验研究结果也证实了以上微观结构参数对锂离子电池的电化学特性有着不可忽视的影响[11-13]。因此科研人员对电极内部结构做了研究，例如许于等[14]将电极中的活性颗粒视为是均匀的，并且是由球形颗粒组成，基于Newman准二维模型[15]，研究了单一活性颗粒粒径均匀分布对电池性能的影响，结果显示由于颗粒粒径的纳米化，锂离子动力电池的倍率性能将大幅提高，只是还未能阐明活性物质颗粒分布不均匀对锂动力电池性能的具体影响；Röder 等[16]把粒径尺寸作为一种分布参数引用到了多孔电极理论中，研究了电极的粒径尺度分布对锂离子电池放电性能的影响，虽然研究了粒径分布对电池性能的影响，但并没有说明不同粒径颗粒对其放电性能的影响。Antartis 等[17]研究了孔隙率对锂离子电池电化学性能和力学性能的影响，结果表明将孔隙率提高到45%并未提高电化学性能，反而降低了力学性能，虽然研究了孔隙率对电化学性能的影响，但未能同时描述迂曲度及粒度分布等结构参数对电化学性能的影响。王慧艳等[18]研究了具有孔隙梯度的电极结构对电池性能的影响，结果表明，孔隙率的梯度分布提高了电解质通量，改善了液相扩散阻力，但是微孔形态以及孔径分布并不是统一的。陈怡沁等[19]基于多孔电极理论，研究了双颗粒粒径均匀分布的电极结构对电池性能的影响，结果表明活性物质颗粒粒径分布均匀可以提高电解质溶液中锂离子的扩散速度，但忽略了电极内部真实的结构，活性颗粒是随机堆叠的，并且孔道是比较迂曲的。Patel等[20]计算了相应的布鲁格曼系数，对不同形态的多孔网络进行了数值模拟，但液相输运阻力对电池的性能有较大影响，通常布鲁格曼关系[21-23]显著低估了液相中锂离子扩散阻力。以上学者对如何提高电池的电化学性能做了一系列的研究，但未能同时考虑真实多孔电极的微观结构参数对电化学性能的影响。杨鹏[24]用电子显微镜研究了多孔电极的微观结构，仅结合实验与计算证明了多孔电极具有分形特性，未能描述结构参数对电池性能的影响。吴伟等[25]结合实验和数值模拟方法对电池正极的有效扩散系数进行了预测，结果表明有效扩散系数受电极微观结构参数的影响，但未能用分形去描述电极结构。将分形理论引入到多孔电极中，分析微观结构参数以及温度对电化学性能的影响，该方面的研究还未见报道。

本工作建立了电极微结构的热-化耦合分形模型，研究了微观结构参数和温度对电解液、固相中锂离子有效扩散系数的影响，并结合数值模拟方法分析了本工作的有效扩散系数模型对放电曲线的影响；运用Comsol 5.6 模拟了锂离子电池的恒流放电过程，并探究了在不同放电倍率情况下负极材料内部不同粒径大小及分布对锂离子电池输出电压与最大容量的影响，为提高锂离子电池的电化学性能提供基础理论参考。

1 多孔电极的分形特征

1.1 孔隙数目与横截面积描述

多孔电极是一种多孔介质，具有分形特性，因此将分形理论引入到多孔电极中，如图1所示。

图1 多孔电极的扫描电子显微镜图[26]Fig.1 SEM photographs of porous electrode[26]

在具有分形特征的多孔电极中，孔径等于或大于λ的孔隙数量总和与孔径大小符合分形标度关系，如式(1)所示[27]：

式(1)中，λ是孔道的平均直径，m；λmax是孔道的最大直径，m；Df是多孔电极的固相分形维数；N是多孔电极中孔径大于或等于λ的累计孔隙数目。

在多孔电极中，由于孔隙数量很大，所以通过计算理论和方法，可把式(1)看成是连续和可微的函数，对式(1)进行微分即可得出：

电极活性物质颗粒分布满足分形特性，则颗粒的总表面积可以表示为：

式(3)中，rs为颗粒的半径，m；rmax,s为颗粒的最大半径，m；rmin,s为颗粒的最小半径，m。

1.2 孔道迂曲特征描述

在多孔电极中，单根管道的长度L(λ)与管道孔径λ的关系符合分形标度关系，可表示为：

式(4)中，L0为孔道流动方向的特征长度，m；Lt是锂离子流动路径的实际长度，m；Dt为迂曲分形维数，该值越大说明孔道就越迂曲。

锂离子在多孔电极中流动时，孔道是迂曲的：0

式(5)中，τ为孔道的迂曲度大于1。

根据式(5)，弯曲管道的迂曲度可以表示为:

孔隙率与颗粒粒径之间的关系为：

式(7)中，ε为孔隙率。

式(8)中，Sv为比表面积，m2；V为立方体体积，m3；As是电极活性颗粒的总表面积，m2。

式(1)～(8)描述了多孔电极结构与孔隙分布情况，是阐述多孔电极内部输运物理现象的主要公式。

2 锂离子电池热模型的建立

锂离子电池在充放电工作过程中，锂电池内部会产生热量，主要由四部分组成，其中副反应热可以忽略。

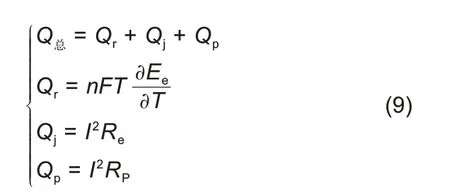
Qr代表电化学反应生成的热量(锂离子在正负极材料上进行嵌入和脱出化学反应的过程中，克服阻力而生成热量)，J；Qj代表欧姆热(锂离子在游离时所受外力影响而形成的热量，其包含电解液和正负极固、液接触面的阻力、电解质溶液的阻力、正负极和集流体边界面的阻力等)，J；QP代表极化热(当电池有电流通过，使电位偏离了平衡电位，该现象被称为极化，极化消耗部分能量并以热的形式释放)，J。

由于副反应生成的热量较低可以省略，因此电池内部总的产热量可表示为：

式(10)中，n是通过隔膜的电荷数；T为热力学温度，K；Ee为电动势，V；I为充放电电流，A；Re为焦耳内阻，Ω；Rp为极化内阻，Ω。由傅里叶定律可知，当电池内部热量升高时，温度随之升高。

3 锂离子电池电化学模型的建立

图2为活性颗粒堆叠电极结构示意图。锂离子电池充放电的整个流程是由锂离子嵌入与脱出的循环往复来完成的，主要有电解液、固相颗粒中锂离子的扩散、Bulter-Volmer电化学动力学方程和电极中电流的传导等过程。充放电过程中，多孔电极固相颗粒与电解液交界处进行电化学反应，锂离子从颗粒内脱出，进入到电解质溶液，再传输到另一个电极颗粒附近，然后电极颗粒与电解质溶液交界处又进行电化学反应，锂离子嵌入到活性颗粒内，进而完成锂离子的脱嵌，同时电子经由外电路实现传递。

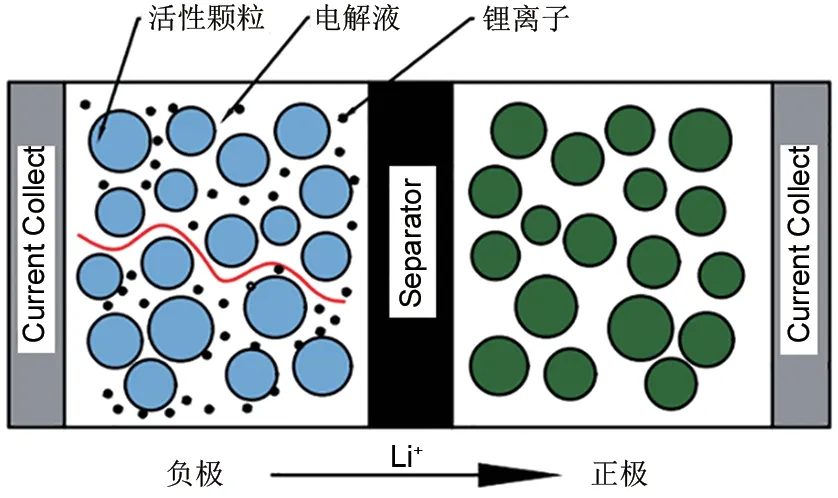
图2 活性颗粒堆叠电极结构示意图Fig.2 Structure diagram of active particle stacking electrode

在对锂离子电池的二维模拟中，可以忽略平行于集流体走向的锂离子扩散情况，仅考虑垂直方向。为更精确地说明数学模型中锂离子扩散过程的控制方程，本工作作以下假设：

①忽略锂离子电池在电化学反应中气体的生成，只考虑液相与固相的作用；

②忽略锂离子电池在运行中的副反应；

③假设电极中的活性物质由球形颗粒构成。

3.1 固相材料中锂离子的扩散

在固相电极中，把活性物质假设为球形，锂离子在活性颗粒内部的扩散可以用菲克定律来描述：

式(12)中，c1是锂离子电池电极中固相颗粒中的锂离子浓度，mol/m3；D1是锂离子在活性物质颗粒中的扩散系数，m2/s；t为时间，s。

在充放电过程中，固相颗粒与电解质溶液交界处进行电化学反应，锂离子由颗粒表面脱离进入电解质溶液中，则从电极颗粒中脱出锂离子的量可表示为：

式(13)中，j是单位面积锂离子脱出电极活性颗粒的通量，mol/(m2/s)。

电极过电位表示实际电势与平衡电势的差值，可由下式表示：

式(14)中，φs、φe分别是固相与液相的电位，V；U是平衡电势，V。在活性物质颗粒与电解质溶液交界处进行的电化学反应可用单位面积脱出锂离子的通量来表示，其动力学过程可用Bulter-Volmer方程式说明，如下式所示：

式(15)中，c1,max是电极材料中锂离子的最大浓度，mol/m3；c1,surf是活性电极材料表面锂离子的浓度，mol/m3；i0是交换电流密度，A/m2；c2是电解质溶液中锂离子的浓度，mol/m3；αc、αa分别是正负极的传递系数；k0是反应速率常数，m/s；R是通用气体常数；F是法拉第常数。

结合式(8)、(13)和(16)，可以得出活性电极颗粒脱出锂离子的通量为：

结合式(8)和(16)得出固相颗粒的锂离子有效扩散系数：

式(17)中，σ是Warburg阻抗因子。锂离子在电极颗粒的脱出与嵌入反应中，固相扩散过程是相当缓慢的，其扩散速率直接决定着电化学反应的快慢。活性物质颗粒的扩散系数越大，则电极的电流放电性能越好，而材料的功率密度越高，高倍率性能也越好，所以固相扩散系数是电极的关键参数之一。

3.2 液相中锂离子的扩散

锂离子在电解液中的扩散控制方程为

式(19)中，Nt是锂离子通过多孔电极的表观通量，mol/(m2/s)；ε是电解液所占的体积即电极的孔隙率；Deff是液相中锂离子的有效扩散系数，m2/s；i是电解质溶液中的电流，A；t+0是锂离子的转移数；x是垂直于电极表面方向的位置。

电解液中锂离子的扩散系数为：

由于电解液中锂离子的传输受多孔电极的结构参数(孔隙率和迂曲度)所影响，因此结合式(6)、(7)和(20)，得到液相中锂离子的有效扩散系数为：

放电过程中，在固、液相交界处进行电化学反应，从活性物质颗粒中脱出的锂离子进入到电解质溶液中，经过扩散到达另外一个电极的颗粒附近。电极内部是由大小不同的颗粒组成，迂曲的孔道以及孔隙分布等限制了锂离子的扩散，使得传输到另外一个电极的总量减少，因此液相中锂离子的有效扩散系数是重要的参数之一。

3.3 建立热-化耦合模型

在充放电过程中，在多孔电极材料与电解质溶液交界处发生电化学反应，锂离子在固相颗粒与电解液交界处进行了嵌入与脱出。由于电化学模型中的浓度和电势的变化导致了产热速率不同，产热量的变化致使电池内部温度发生改变，温度的变化又反过来影响电化学模型中容易受温度影响的物理化学参数(如固、液相中锂离子的有效扩散系数及电导率等)。在一定的范围内，温度升高使得固、液相中锂离子的有效扩散系数增大，促进锂离子的迁移，同时电导率也随之增大，温度降低则反之；当温度发生变化时，电极的反应速率随之改变，若电池电压保持恒定，影响电池的功率输出，同时温度影响电解液的传送速度，电池充放电性能也会受到影响。

图3 是锂离子电池的热-电化学耦合模型。根据生热传热机理，结合锂离子电池热模型中温度的变化和电化学过程，将计算得到的锂离子电池温度应用到电化学模型中，作为电化学反应的初始温度；并且将电化学反应过程中产生的热传入到热模型里，作为此时电池的产热，经过参数的传递，实现锂离子电池热-化模型的耦合。

图3 热-电化学耦合模型原理示意图Fig.3 Schematic diagram of thermal electrochemical coupling model

4 结果与讨论

4.1 数值分析

对建立的有效扩散系数分形模型进行数值模拟，分析电极微观结构参数以及温度对固、液相有效扩散系数的影响，结果如下。

图4为在不同的迂曲分形维数Dt下，电解液中锂离子有效扩散系数Deff随孔隙率的变化关系。模拟表明，锂离子的有效扩散系数随孔隙率的增大而增大；当多孔电极的孔隙率相同时，迂曲分形维数越小，锂离子的有效扩散系数越大。由于迂曲分形维数越小，孔隙通道的迂曲程度越小，锂离子在扩散过程中受到的阻力越小，从而有利于锂离子的传输。

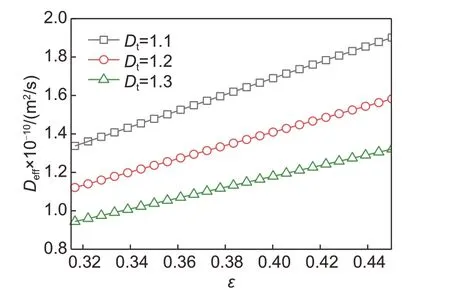
图4 迂曲分形维数Dt对有效扩散系数Deff的影响Fig.4 Effect of tortuous fractal dimension Dt on effective diffusion coefficient Deff

图5为在不同的面积分形维数Df下，电解液中锂离子的有效扩散系数与迂曲度的关系。结果表明，锂离子的有效扩散系数随迂曲度增大而减小；当多孔电极迂曲度相同时，面积分形维数增大，有效扩散系数随之增大。由于面积分形维数越大，多孔电极中大粒径颗粒分布较多，从而孔隙率增大，流动性提高，有利于锂离子的传输，因此锂离子的有效扩散系数增大。

图5 面积分形维数Df对有效扩散系数Deff的影响Fig.5 Effect of area fractal dimension Df on effective diffusion coefficient Deff

图6为固相有效扩散系数随面积分形维数的变化趋势。模拟表明，当面积分形维数增大时，固相有效扩散系数随之减小。由于面积分形维数增大，负极区域内大粒径颗粒分布较多，颗粒内部的锂离子扩散路径增大，导致锂离子的脱出量减少，因此固相有效扩散系数减小。

图6 面积分形维数Df对固相有效扩散系数Ds的影响Fig.6 Effect of area fractal dimension Df on effective diffusion coefficient Ds of solid phase

图7(a)、7(b)分别为锂离子在固、液相中的有效扩散系数随温度的变化关系。由数值分析可知，在一定的温度范围内，固、液相中锂离子的扩散系数随温度升高而增大。因为温度升高会促进锂离子的传递，使其在局部区域内形成浓度差，从而使锂离子在单位面积上的扩散量增加，因此有效扩散系数增大。

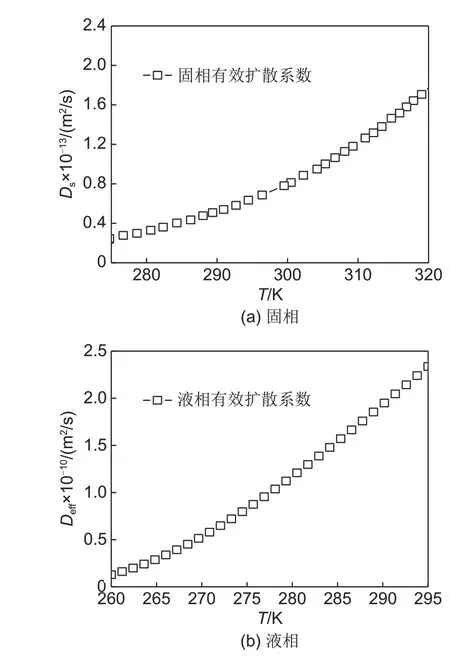
图7 温度T对固、液相有效扩散系数的影响Fig.7 Effect of temperature on effective diffusion coefficients of solid and liquid phases(a)solid phase;(b)liquid phase

4.2 分析锂电池性能的影响因素

将本工作的分形模型与实验数据、无分形模型做对比，实验数据来源于商用LiMn2O4电池[28]。由图8可知，模拟分形模型得到的放电曲线与实验数值的电压趋势和容量大小更相近，因此本工作的分形模型是更准确的。

图8 0.5 C下得到的放电曲线与实验测定的数值对比图Fig.8 Comparison between the discharge curves obtained under 0.5 C and the values measured by experiment

图9为液相中不同锂离子的有效扩散系数对放电曲线的影响。图9(a)是以简单的bruggman 因子作为参数计算得到的有效扩散系数，将其代入仿真模型中得到的放电曲线；图9(b)是考虑了电极微观结构参数(迂曲分形维数、面积分形维数、孔隙率和迂曲度等)对电池性能的影响，推导出了有效扩散系数的分形模型，并进行仿真计算得到的放电曲线。由图中数据可知，放电趋势大致相同，但电池最大放电量不同，因此考虑电极微观结构参数推出的分形模型，更符合实际的电极结构。

图9 不同的液相有效扩散系数对放电曲线的影响Fig.9 Effect of different liquid phase diffusion coefficients on discharge curves(a)with bruggman factor as parameter(b)considering the actual microstructure parameters of the electrode

图10 为不同的固相有效扩散系数对放电曲线的影响。由图可知，在0.5 C 倍率下放电时，随着固相有效扩散系数减小，放电的最大容量基本保持不变；在2.0 C 倍率下，固相有效扩散系数减小，放电的最大容量减小。表明在相对高倍率的放电过程中，固相有效扩散系数对放电的最大容量有较显著的影响。由于锂离子的固相有效扩散系数增大，从活性物质颗粒中脱出的锂离子的量增大，使得扩散到另一电极的锂离子通量增加，因此放电的最大容量增加。

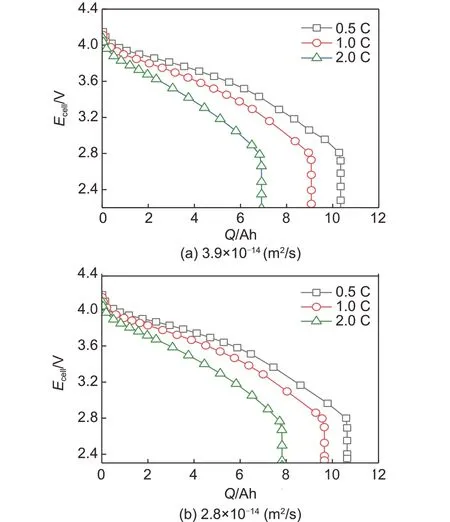
图10 不同的固相有效扩散系数对放电曲线的影响Fig.10 Effect of different solid effective diffusion coefficients on discharge curves

图11 为正极不同面积分形维数的锂离子电池在不同倍率下的放电曲线。由图可知，在0.5 C 倍率下放电，随着面积分形维数的减小，放电的最大容量基本保持不变；在2.0 C 倍率下放电，随着面积分形维数的减小，放电的最大容量逐渐增大。表明在相对高的放电倍率下，多孔电极区域内部面积分形维数对于锂离子电池的电化学性能有显著的影响。由于面积分形维数越小，正极内部小粒径颗粒分布越多，从而活性颗粒中锂离子的扩散路径变短，使得锂离子更易脱出，因此放电的最大容量增加。

图11 正极不同面积分形维数的锂离子电池在不同倍率下的放电曲线Fig.11 Discharge curves of lithium-ion batteries with different area fractal dimensions of the positive electrode at different magnifications

5 结 论

（1）本工作建立了电极微结构有效扩散系数的分形模型，此模型受面积分形维数、迂曲分形维数、孔隙率、迂曲度及颗粒粒径等参数的影响。在迂曲分形维数和面积分形维数相同情况下，液相中锂离子的有效扩散系数随颗粒粒径比值增大而增大；与通过Bruggman因子计算得到的有效扩散系数相比，考虑电极微观结构参数的有效扩散系数分形模型更符合实际。

（2）在相对高倍率的放电过程中，正极内部结构面积分形维数越小，放电容量越大。由于面积分形维数减小，正极内部小颗粒分布较多，使得锂离子在活性颗粒中扩散的路径越短，活性颗粒中的锂离子更易脱出，因此锂离子的脱出量越多，放电的最大容量越大。

（3）建立了热-电化学耦合模型；锂离子电池在充放电过程中，电极活性物质颗粒与电解质溶液交界处发生电化学反应，锂离子在脱嵌过程中受到阻力的作用而产生热量，随着热量的增加，电池内部的温度升高，温度又进一步加快了固、液相中锂离子的扩散，促进了电化学反应的进行，从而温度与固、液相扩散系数耦合影响锂离子电池放电过程。