肋片增强式梯级相变储热系统放热特性的三维数值

沈永亮，张朋威，刘淑丽

（北京理工大学机械与车辆学院，北京 100081）

梯级相变传热技术按照“温度对口，梯级利用”的原则，将相变温度不同的相变材料在吸/放热过程中按相变温度降/升序的方式进行排布。在相变蓄热过程中，放热流体的温度沿流动方向减少，而相变蓄热材料的熔点温度也在阶梯降低，保证相对恒定的温度差，以提高整体的储/放热效率[1]。

科技工作者对梯级相变储热系统进行了大量的数值研究，目的主要是证实具有多个PCM 的梯级相变储热系统比具有单个PCM 的相变储热系统具有更好的热性能。传统的物理模型包括板式换热器[2-4]、管式换热器[5-6]、圆柱形同心换热器[7]。为了进一步体现梯级相变储热技术在蓄热方面的优势，学者们开发了创新的物理模型。Yang等[8]、Wu等[9]和Alptekin等[10]在低温和高温领域提出了PCM胶囊填充床系统。Hu等[11]和Rudra等[12]开发了低温范围内的截锥形和锥形换热器。事实证明，与传统的圆柱形梯级相变储热单元相比，锥形模型在传热效率和储能方面具有优势[13]。在最新的研究中，Wang等[14]提出了一种带有梯级PCM胶囊的新型旋转再生热交换器。该模型旨在解决燃煤电厂的泄漏、热变形和堵塞问题。已经开发和验证了不同物理模型的数学模型。该系统通常被简化为一维或二维模型。1996年，Gong等[15-16]提出了复合PCM板的有限元相变热传导模型。数值结果表明，与单一PCM 相比，使用不同熔点的复合PCM 可以大大提高充电和放电倍率。对于使用多个PCM 的管壳式潜热蓄热单元，Fang等[17]开发了基于焓的数学模型。

已有的关于梯级相变储热系统的数值研究通常是通过建立一维或二维数学模型完成的，很难真实反映储热器结构对系统性能的强化作用。此外，大部分的学者注重对PCM 储热过程的热性能进行研究，而实际上由于PCM 在放热过程中热传导占主导作用，相比于储热过程具有更低的传热速率，应当对梯级相变储热系统的放热过程开展研究。本工作创新性地设计了一种肋片增强型三管式梯级相变储能系统，并建立了三维数值模型，研究系统放热过程中各级PCM 的性能变化规律，探究传热流体进口温度和PCM 初始温度对系统放热速率的影响规律，为强化梯级相变储热系统传热的设计优化提供指导。

1 数值模型建立与实验验证

1.1 物理模型

选取月桂酸、石蜡和硬脂酸作为梯级相变储能系统的PCM，具体的物性参数在前期已发表的文献[18]中。设计一种梯级相变储能系统，由三级串联的肋片增强型三管式储热器构成。储热器的结构如图1 所示，内管和外管为传热流体(HTF)，中管为封装PCM 的腔体，矩形肋片与内外管道均匀连接。为了使得传热流体与PCM 换热时达到稳定流动状态，在储热器的两端设置了密封盖，几何参数如表1所示。

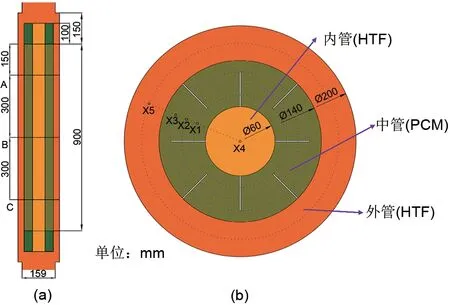
图1 相变储热器结构示意图Fig.1 Schematic diagram of the latent heat storage unit

表1 相变储热器物理模型的具体几何尺寸参数Table 1 The specific geometric parameters of the physical model of the latent heat storage unit

建立了三维仿真物理模型，考虑到物理模型结构较为复杂且存在多域计算，采用非结构化混合型网格，内外直肋片和相变区域做加密处理保证计算结果更加准确，对各类边界和几何体进行命名，边界层设置为5层平滑过渡，网格增长率为1.2，过渡比为0.2。此外，相同区域的接触面进行组合处理，便于后期FLUENT 求解器中边界条件的耦合设置。梯级相变储热系统物理模型和网格结构如图2所示。

1.2 数学模型

对三维传热模型做出了下列假设[19]：

①相变材料热物性参数始终保持不变；

②相变材料密度采用Boussinesq假设，考虑浮升力作用；

③忽略系统的黏性耗散；

④储热器外壁面被认为绝热，忽略系统的热损失。

求解区域可以分为传热流体区域和相变材料区域，两个控制区域内的流动传热受质量守恒、动量守恒以及能量守恒三大定律共同作用。方程的具体形式如下所示。

（1）传热流体区域

连续性方程

式中：v分别为在x，y，z方向上的速度分量，m/s；μf为热流体运动黏度，Pa·s；λf为传热流体导热系数，W/(m·K)；Cpf为热流体定压比热容，J/(kg·K)；ρf为热流体密度，kg/m3；T为储热器内热流体温度，K。

（2）相变材料区域

式中，ε为随机小数(小于0.0001，防止出现分母为0的情况)；C为糊状区常数(理想值介于10-5和10-6，此处取10-5)；v为流动速度矢量，m/s；vp为牵引速度矢量，m/s；β为PCM的液相率。

式中，λs为金属肋片的导热系数W/(m·K)；ρfin为金属肋片的密度，kg/m3；Cp，fin为金属肋片的比热容，J/(kg·K)；TPCM为相变材料的温度，K；Tfin为金属肋片的温度，K。

1.3 边界条件设置

根据梯级相变实验系统的运行情况，三维数值模型的进口边界条件为恒定进口温度和流速，即为：

储热器外管壁面为绝热壁面，对应外壁面边界条件为：

计算域初始化温度：

2 数值计算方法和模型验证

2.1 数值计算方法

计算模型中使用k-epsilon湍流模型并激活浮力作用项，PCM的相变过程是基于Solidification/Melting模型处理的。采用压力和速度耦合方式的Coupled求解方法[21]，压力修正方程为采用PRESTO 方案，其他各项方程离散方式均使用二阶迎风格式。压力、密度、速度、液相分数、能量亚松弛因子分别设为0.3 MPa、0.5 kg/m3、0.7 m/s、0.8和0.9。

2.2 模型验证

在本次模拟中，划分了4组网格，网格数分别为428198、922625、2143483、3149660。在相同的求解器参数设置前提下，分别对以上4种网格数的数值模型进行计算，采用相变区域体积加权平均方法来表示相变区域的相变情况，得到了不同网格数下PCM 的液相率随温度的变化情况。为了确定数值模拟的时间步长，选择了3种时间步长进行验证，分别为0.1 s、0.5 s 和1.0 s，比较了3 种时间步长PCM 的液相率变化情况。为了验证数值模型的准确性，搭建了与物理模型完全一致的实验系统，如图3所示。在进口温度为373.15 K，进口流速为4.8 m/s 的条件下对数值模型的加热和放热过程进行了验证。

图3 梯级相变储热实验系统的示意图和实物图Fig.3 Schematic diagram and physical map of the experimental cascaded latent heat storage system

如图4(a)所示，由网格数922625 向网格数2143483 过渡时，液相率达到1 时的时间变化明显，而网格数继续增长到3149660后时间则几乎没有变化，认为此时已经达到了网格无关要求，最终确定最优网格数为2143483。时间步长无关性验证如图4(b)所示，时间步长分别为0.1 s、0.5 s 和1.0 s 时，PCM 的液相率变化几乎相同，为了节约计算时间成本，选择1.0 s 作为数值模拟的时间步长。实验数据与模拟数据的温度变化趋势如图4(c)所示。可以看出，两组数据能够较好地吻合，证明数值模型以及求解方法的正确性与可靠性。

图4 网格无关性验证和数值模型验证Fig.4 Verification of mesh independence and numerical model

3 结果与讨论

3.1 各级PCM的温度和液相率变化特性

换热流体为水，进口温度为300 K，流速为0.4 m/s，保证在换热器内为湍流状态，设置各级PCMs 初始化温度为373 K。图5 为放热过程PCM温度和液相率随时间的变化情况。从图5中可以看出整个放热过程分为3个阶段，分别为液态显热放热阶段、潜热放热阶段和固态显热放热阶段，显热放热阶段相变材料温度变化明显，潜热放热阶段相变材料温度则相对恒定。放热初期3种PCMs具有相同的降温速率，PCM1、PCM2 和PCM3 依次达到凝固区间。PCM3与传热流体的温差最小，导热系数也偏低，整体换热速率较慢，故呈现出较长的潜热放热阶段。PCM2 具有较高的导热系数，PCM1则与热流体温差较大，所以PCM1和PCM2的整体换热速率几乎相同。与PCM1相比，PCM2较快结束潜热放热进入固态放热阶段，PCM3则耗时较长，这是由于PCM2 的相变焓值略低于PCM1，而PCM3 的整体换热速率最低，PCM3 达到热平衡状态时认为系统放热过程完成。从图5(b)中可以看出在PCM1和PCM2液相率表现出了一致性，几乎同时开始凝固并在60 min 时完全凝固，而PCM3潜热放热阶段用时较长，凝固时间明显晚于PCM1和PCM2，在120 min左右完全凝固。

图5 梯级相变系统放热过程温度和液相率演变规律Fig.5 Evolutions of PCM temperature and liquid fraction during discharging process

在整个放热过程选取5个典型时间点(第20 min、40 min、60 min、80 min和100 min)进行分析，选取截面为3个相变换热器的中层传感器对应截面(Z=0.75 m)，梯级相变放热过程中的温度分布与液相率分布见图6。从图6 中可以看到各个截面内相变材料温度最高点都出现相变材料的中心区域，温度最低点则在换热壁面和肋片周围。各个换热器的横向温度进行对比，发现放热初期PCM1到PCM3的温度呈现递减趋势，这是由于PCMs都处于恒温潜热放热阶段，相变熔化温度呈现梯级递减趋势，而在放热后期时PCM1 和PCM2 已经完全凝固为固态，显热放热温度下降较快，所以又呈现PCM3温度高于PCM1和PCM2的情况。通过纵向对比可以观察到放热过程中PCMs 温度随时间的变化规律，放热初期每个换热器内相变材料的温度都趋向于均匀分布，此时PCMs都处于潜热放热阶段，随着放热时间的增加，换热壁面和肋片周围温度较低，贴壁处相变材料逐渐凝固，PCMs温度分布不再均匀存在明显的温度梯度，表现为周围环状低温区域，此时固体PCM 附着在换热壁面上形成热阻，减缓换热速率。随着放热过程的进行，PCM2率先完全凝固，其次是PCM1，最后是PCM3，而后固态PCMs 温度会持续下降至热平衡状态。图6 中可以观察到放热过程PCMs液相率的变化规律，在放热过程初期贴近换热壁面和肋片处PCM1和PCM2先凝固，出现部分液相率为0 的蓝色区域，此时PCM3 刚开始进入潜热放热阶段，液相率开始变化，随着放热的进行PCM1和PCM2凝固区域逐渐扩大，表现出一致的液相率变化规律，而PCM3液相率变化则较为缓慢，在PCM1和PCM2完全凝固50 min后PCM3完全凝固，PCM3的放热滞后性与温度分布规律一致。

图6 放热过程温度分布图(上侧)与液相率分布图(下侧)Fig.6 Contours of PCM temperature(Upper side)and liquid fraction(Under side)

3.2 传热流体进口流速对系统放热过程的影响

分别选取4种不同的传热流体进口流速(0.1 m/s、0.4 m/s、0.7 m/s 和1.0 m/s)进行放热过程的模拟研究，各级相变材料的初始化温度均为373 K，传热流体进口温度为300 K，放热过程模拟只改变热流体的进口流速，其余边界条件设置参数保持一致。传热流体进口流速对3 种PCM 的影响规律类似，以PCM2为例进行分析。PCM2温度和液相率随进口流速的变化规律见图7。从图7(a)中可以看出进口流速并不会改变相变放热过程的温度总体演变规律，尤其是在放热初期的液态显热放热阶段，几组PCM2的降温速率几乎相同，而潜热放热时间则会因进口流速的增大有所减短，相应地达到最终热平衡状态时间也会缩短，这是由于流速增加后热流体湍流更加剧烈，与PCMs进行强制自然对流换热，换热速率上升导致相变时间缩短。但随着进口流速的进一步增加，换热速率的增强作用开始明显减弱，原因是大进口流速也会导致更大程度的动能损失，强制对流作用受此影响存在上限。从图7(b)的液相率变化规律可以看到PCM2的液相率总体变化趋势相同，进口流速增大，液相率先下降至稳定值意味着PCM 率先完全凝固，但随着进口流速的增加，液相率之间的差异明显缩小，这点与温度分布规律表现相似，说明流速对传热增强作用会随着进口流速的增大而减弱，建议在实际梯级相变放热过程中考虑增速经济成本，选择适当的换热流体进口流速以保证系统更好的热性能。

图7 PCM2温度和液相率随进口流速的变化Fig.7 Evolutions of PCM2 temperature and liquid fraction with changiny inlet flow rate

3.3 PCMs初始温度对系统放热过程的影响

采用3 组PCMs 初始温度进行数值模拟研究，分别为353 K、363 K 和373 K，热流体为水，进口温度为300 K，流速为0.4 m/s。同样，PCM 初始温度对3 种PCM 的影响规律类似，以PCM2 为例进行分析。放热过程中PCM2 温度和液相率随PCM初始温度的变化规律见图8，从图8(a)中可以看出PCMs初始温度对PCM2温度变化趋势影响很小。由于PCM2初始化温度为373 K时，与热流体的温差较大，具有较高的换热速率，但同样因为温差大的原因温度下降至凝固温度所需时间也会延长，所以总体上与初始温度为353 K 和363 K 的放热时间差异较小。此外，可以看到初始化温度的升高对整个潜热放热阶段的作用在慢慢减弱，同时还会加大热量损失，因此实际放热过程中应该选择适当的PCMs初始温度。PCM2的液相率变化规律见图8(b)，可以看出液相率先行下降的也率先稳定，总体凝固时间差别不大，PCMs 初始温度变化对PCM2的潜热放热阶段影响较小。

图8 PCM2温度和液相率随初始温度的变化规律Fig.8 Evolutions of PCM2 temperature and liquid fraction with initial temperature

4 结 论

设计了一种肋片增强型三管式梯级相变储能系统以提高相变材料的传热速率，建立了三维数值仿真模型，针对系统放热过程中各级相变材料的性能展开研究，并探究了传热流体进口流速和相变材料的初始温度对系统性能的影响规律，并得出以下结论。

（1）在放热过程中，各级PCM 相变不会同时发生，受到储热材料的相变温度和潜热的影响最大。在本研究中，PCM1和PCM2首先开始和结束相变放热过程，PCM3由于相变温度最低，最后开始和结束相变放热过程。

（2）传热流体进口流速的增大会提高相变材料的放热速率，但随着流速的进一步增加，放热速率的提高程度明显减弱。在实际梯级相变储热系统的放热过程中应当考虑经济性，选择适当的传热流体进口流速以保证系统更好的热性能。

（3）较大的相变材料初始温度会带来较大的传热温差，具有较高的换热速率，但同样因为温差大的原因温度下降至凝固温度所需时间也会延长。因此，相变材料的初始温度对显热放热过程具有一定的影响，但对于潜热放热阶段影响较小。

符号说明

C—— 比热容，J/(kg·K)

H—— 焓值，J

L—— 相变材料的潜热，J/kg

m—— 质量，kg

Q—— 热量，J

T—— 温度，K

V—— 速度，m/s

ϕ—— 复合多孔相变材料孔隙率

ρ—— 密度，kg/m3

μ—— 动力黏度，Pa·s

λ—— 导热率，W/(m·K)

β—— 相变材料的液相率

下角标

f—— 传热流体

liquid—— 液态相变材料

i—— 第i级相变储热器

in—— 入口边界

out—— 出口边界

PCM—— 相变材料

solid—— 固态相变材料

0—— 初始状态