关注图形结构 衍生通性通法
——对一道“倍半角”问题的再思考
段广猛
(江苏省苏州工业园区星湾学校)
图形结构是几何学的灵魂,也是解几何题的关键.在几何解题教学中,教师要善于从问题的已知条件、图形的结构特征以及结论的合理导向入手,触发广泛联想,衍生出相关的解题策略,从而灵活地构造一些常见的基本图形,使分散的条件集中化、隐含的条件显性化、复杂的条件简单化.这样的解题教学才可以活化学生思维,积累解题经验,实现创新思维能力的提升,达到举一反三、触类旁通的解题效果.
下面以一道“倍半角”问题为例,从图形的核心结构入手,联想一些常见的解题策略,进行一次再思考,以深入挖掘该题对提升学生解题思维能力的价值.
一、原题呈现
题目如图1,在△ABC中,∠A=40°,AB=AC,P为边AB上的一点,且∠ACP=20°,求的值.
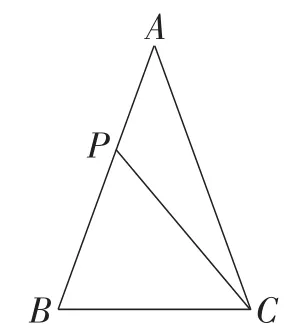
图1
二、结构分析
此题图形结构简洁,各元素之间的关系都是确定的.从角度的视角进行分析:∠A=40°,∠ACP=20°,∠ABC= ∠ACB=70°,∠BCP=50°,∠BPC=60°,∠APC=120°;从线段的视角进行分析:AB=AC,AP+BP=AB.这些比较显性的条件中,大多都是非特殊角,尽管图形确定,但从初中范畴来看,还是很难操作的.由此,还要挖掘一些隐性条件.
例如,∠A=2∠ACP,可以说,这是此题的核心结构,由此可联想系列常见的“倍半角”构造方式,衍生出一类“倍半角”解题策略.
再如,∠BPC=60°(或∠APC=120°),这是图中独有的特殊角,由此可联想“边对角”结构,即“边BC对∠BPC”(或“边AC对∠APC”)结构,衍生出构造辅助圆的解题策略.
当然,由于此题结构明确,图形确定,从高中范畴来看,还可以衍生出解三角形等解题策略,以算代证.
下面逐一分析相关的解题策略.
三、解题策略
策略1:由“倍角造半角”
“倍半角”结构,即∠A=2∠ACP,是此题的核心结构.初中阶段“倍半角”结构的常见处理策略无非两条路径:一是由“倍角”造“半角”,即将“倍角”半分;二是由“半角”造“倍角”,即将“半角”加倍.这两条路径往往与等腰三角形的外角模型或角平分线相结合.
图2或图3是两种常见的由“倍角”造“半角”的方式,由此可衍生出以下9种解题方法.
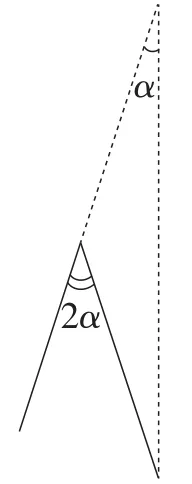
图2

图3
方法1:见角平分线,作双垂线.
如图4,延长BA至点D,使AD=AC,连接CD,
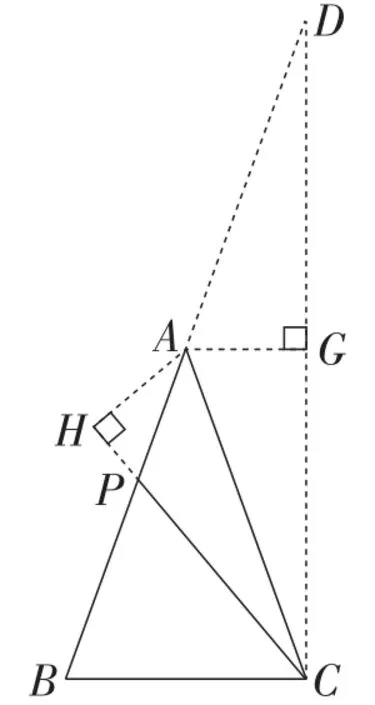
图4
则∠D=∠ACD=20°,且AD=AB.
易证CA平分∠PCD.
过点A分别作CD,CP的垂线,垂足分别为点G,H,
则AG=AH.
又易证BC=2AG,则BC=2AH.
方法2:角平分线的对称性.
如图5,同方法1作相关辅助线,可得CA平分∠PCD.
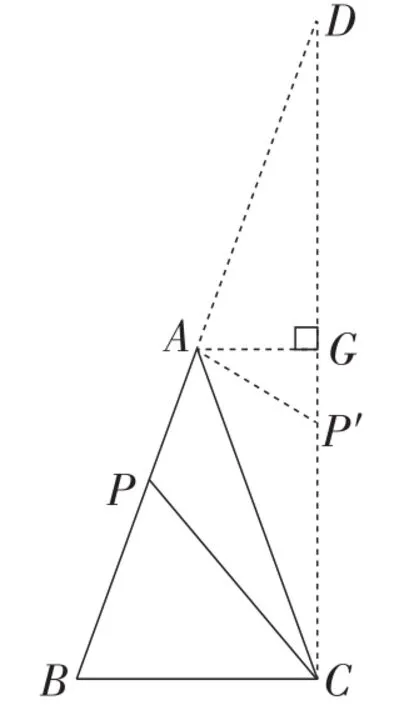
图5
作点P关于AC的对称点P′,则点P′落在CD上,且AP=AP′,∠AP′C= ∠APC=120°.
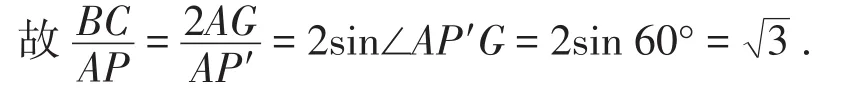
【反思】以上两种解法都是基于如图2所示的“由倍角造半角”的策略,结合角平分线的对称性而得到的.前者“见角平分线,作双垂线,得相等”,后者“见角平分线,作对称,得相等”,这都是角平分线常见的处理策略,集中体现了其对称性这一本质属性.“由倍角造半角”,从而“得等角”,还体现了转化思想.另外,这两种解法都涉及等腰三角形之“三线合一”的性质.
方法3:相似法.
如图6,延长CA至点Q,使AQ=AP,连接PQ,

图6
则∠Q=∠APQ=20°.
故∠Q=∠PCQ.
从而PQ=PC.
注意到∠APQ+∠B=90°,作CG⊥AB于点G,AH⊥PQ于点H,
则△BCG∽△APH.

方法4:全等法1.
如图7,作等腰三角形ABC的顶角平分线AM,交CP于点O,

图7
易得∠OAP=∠OAC=∠OCA=20°.
则OA=OC.
在OM上取点Q,使OQ=OP,易证得△OAP≌△OCQ.
则AP=CQ,∠OPA=∠OQC=120°.

方法5:全等法2.
如图8,同方法4作相关辅助线,可得OA=OC.
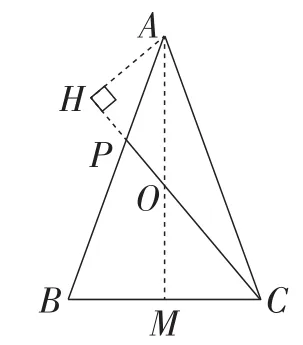
图8
再过点A作OP的垂线,垂足为点H,
易证△OAH≌△OCM.
则CM=AH.

【反思】全等与相似是特殊与一般的从属关系,它们是计算线段长度或比例的常见方法.方法3是基于如图2所示的“由倍角造半角”的策略,结合等腰三角形“三线合一”性质,从而构造三角形相似求得线段之间的比例.值得一提的是,这种构造方式恰好将两个目标线段(BC,AP)置于两个相似三角形中,即这两条线段之比恰为相似比.方法4、方法5都是基于如图3所示的“由倍角造半角”的策略,即“作角平分线,得等角,现等腰”,然后构造全等转移线段,从而将两条目标线段转移到同一个三角形中,顺利获解.
方法6:图形变换法1.
如图9,作等腰三角形ABC的顶角平分线AM,则BC=2CM.

图9
将△ACM沿着AC翻折至△ACM′,则CM=CM′,且∠CAM=∠CAM′=∠ACP=20°.
从而∠PAM′=60°,且CP∥AM′.
再作PH⊥AM′于点H,易得CM′=PH(相当于将CM′平移至PH).

方法7:图形变换法2.
如图10,同方法6作相关辅助线,将AP平移至QC处,易证∠CQM′=∠PAM′=60°.
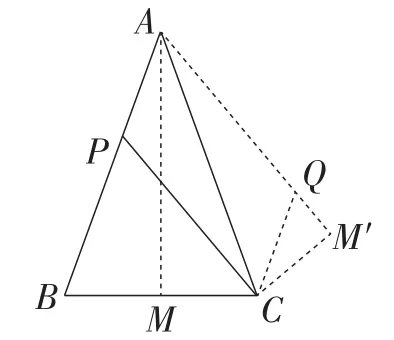
图10

方法8:“由倍造半”+图形变换法3.
如图11,作等腰三角形ABC的顶角平分线AM,将△ACP沿着AC翻折至△ACP′,再作P′N⊥AM于点N,

图11
易证BC=2CM=2P′N,∠P′AN=60°.
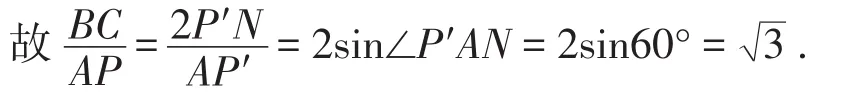
【反思】翻折、平移都是常见的图形全等变换,也是转移线段的重要方式.方法6~8都是基于如图3所示的“由倍角造半角”的策略,结合翻折变换及平移变换,从而将两条目标线段转移到同一个三角形中,顺利获解.如果构造全等或相似是一种静态的思考方式,那么图形变换就是一种动态的思考方式,也是一类问题解决的重要途径.
方法9:面积处理法.
如图12,作等腰三角形ABC的顶角平分线AM,交CP于点O,易证∠OAC=∠OCA=20°.

图12
则OA=OC.
将等腰三角形ACO沿着AC翻折至△ACO′,
易证四边形AOCO′为菱形,且∠PAO′=60°.
过点P作PG⊥AO′于点G,
易得S菱形AOCO′=AO·CM=AO′·PG.
又因为AO=AO′,
故CM=PG.

【反思】面积法是计算线段长度或比例的又一重要策略.方法9仍先利用如图3所示的方式“由倍角造半角”,结合翻折变换构造菱形AOCO′,再借助面积处理,得到菱形每条边上的高相等,实现线段的转移,从而将两条目标线段转移到同一个三角形中,顺利获解.
以上9种解题方法都是基于“倍半角”结构而采取的“由倍角造半角”的常见构造方式,然后结合角平分线、全等、相似、图形变换,以及面积等常见的处理策略而获解的.下面再看几种“由半角造倍角”的常见思路.
策略2:由“半角造倍角”
图13或图14是两种常见的由“半角”造“倍角”的方式,由此可衍生出以下4种解题方法.
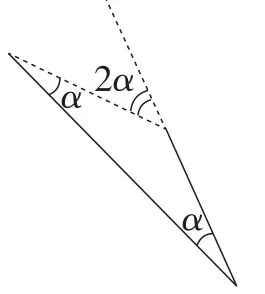
图13

图14
方法10:相似法1.
如图15,在AC上取点D,使PD=CD.

图15
则∠ADP=2∠ACP=∠A=40°.
故AP=PD=CD.
从而BP=AD.
注意到∠A+∠BCP=90°,作PG⊥AD于点G,BH⊥PC于点H,
易证△BCH∽△APG.

方法11:相似法2.
如图16,在AC上取点D,使PD=CD.
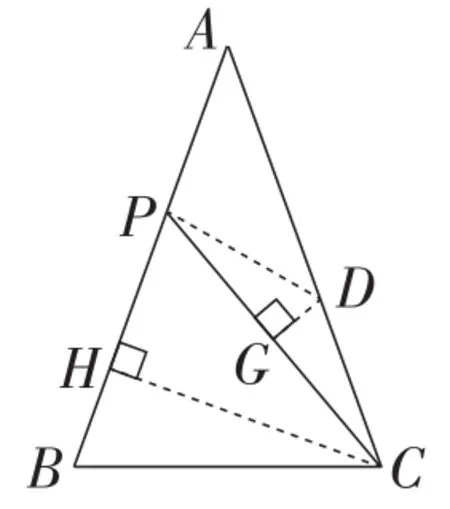
图16
同方法10,可得AP=PD=DC.
注意到∠PCD+∠B=90°,作DG⊥PC于点G,CH⊥AB于点H,
易证△BCH∽△DCG.

方法12:相似法3.
如图17,在AC上取点D,使PD=CD.

图17
同方法10,可得AP=PD=DC.
作点C关于AB的对称点C′,连接CC′交AB于点H,再连接BC′,
易证△BCC′∽△DCP.

【反思】方法10~12都是基于如图13所示的“由半角造倍角”的策略,构造出等腰三角形,再利用相似解决问题.“倍半角”问题的构造模式常与等腰三角形相结合,无论是“由倍造半”还是“由半造倍”,往往会出现等腰三角形,从而实现等角转化.
方法13:翻折变换.
如图18,将△ACP沿CP翻折至△A′CP,连接AA′,延长CP交AA′于点G,

图18
则∠ACA′=2∠ACP= ∠BAC=40°.
易证△ABC≌△CAA′.
故BC=AA′.
又由CP平分∠ACA′,可得CG⊥AA′,且AA′=2AG.

【反思】翻折变换也是一种常见的“由半角造倍角”的构造方式,然后巧识全等实现线段的转化,从而将两条目标线段转移到同一个三角形中,顺利获解.
以上4种解题方法都是基于“倍半角”结构而采取的“由半角造倍角”的常见构造方式,然后结合全等或相似等常见的处理策略而获解的.
策略3:边对角→辅助圆
图19是“边对角”的核心结构,可联想构造辅助圆,由此衍生出以下2种解题方法.

图19
方法14:导边导角.
如图20,作△BCP的外接圆⊙O,连接OB,OC,OP,再连接AO并延长交BC于点M,
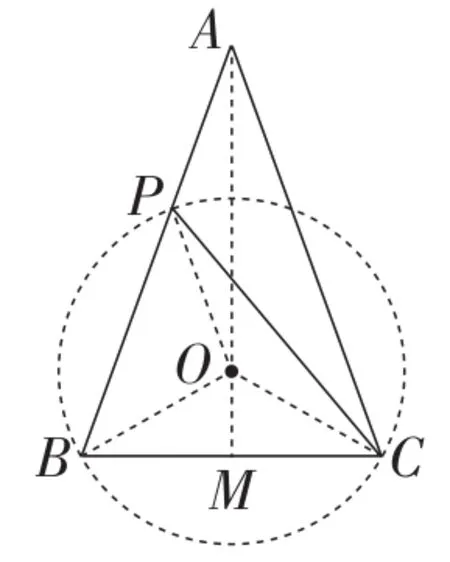
图20
由AB=AC,且OB=OC,易证AO垂直平分BC.
又由∠BOP=2∠BCP=100°,则∠OPB=40°.
易知∠OAP=20°.
故∠AOP=20°.
从而AP=OP=OB.
方法15:全等法.
如图21,作△ACP的外接圆⊙O,在优弧⌒AC上取点D,使DA=DC,连接DP,

图21
易证△ACD为等边三角形,且∠ADP=∠ACP=20°,∠APD= ∠ACD=60°.
再过点A分别作BC,DP的垂线,垂足依次为点M,N,
易证△ACM≌△DAN.
故CM=AN.

【反思】以上2种解题方法都是基于“边对角”结构的识别(即“边BC对∠BPC”或“边AC对∠APC”),而采取的构造辅助圆策略,然后利用全等导边、导角,顺利获解.“边对角→辅助圆”是一种常见的处理策略,往往能起到意想不到的解题效果.
图形结构决定图形性质,很多问题解决的密钥自然也蕴含于图形结构中,识别并完善图形结构中的一些关键部位,便可获取系列常见的解题思路.
四、特殊化与一般化
数学家梅森认为,特殊化与一般化贯穿于整个解题过程中,或者说,特殊化与一般化构成了整个解题过程的基础.他还指出特殊化在解题中的作用:第一,只有通过特殊化才能很好地了解所面临的问题;第二,只有通过特殊化才能认识导致一般化的模式;第三,对于所得出的结论又必须借助进一步的特殊化去检验.
一般化是问题解决的另一条重要途径,它是数学创造的基本形式.数学认识的根本目的是揭示更为普遍、更为深刻的事实或规律,只有将问题推广到更一般的情形,才能获得更加本真的认知,才能得到更多的收获.
对于此题,若做特殊化处理,可得到如下简单的结论:如图22,在等边三角形ABC中,P为边AB上一点,且∠A=2∠ACP,显然.

图22
若做一般化处理,可得到如下结论:如图23,在△ABC中,AB=AC,P为边AB上的一点,且∠A=2∠ACP,试说明:
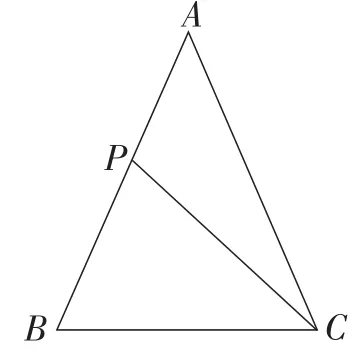
图23
经尝试,以上15种解题方法对于此类一般化问题均适用.由此看来,它们都是处理此类问题的通性、通法.
五、几点思考
1.关注图形结构,联想通性通法
几何解题教学中,教师应善于从图形的结构入手,引导学生洞察图形的结构特征,构造相关的基本图形,从而引发学生广泛联想,衍生出一些常见的解题策略.本文前13种解题方法都是基于图形的核心结构(即“倍半角”结构)而触发联想的“倍半角”构造法;方法14与方法15是基于“边对角”结构而触发联想的辅助圆构造法.总之,图形结构是几何问题的“魂”.教学中,教师理应引导学生从识图入手,整体把握图形结构,合理地对图形结构进行拆解、提炼,发挥基本图形的导航作用,实现边或角之间的相互转化.
通性通法是解决一类问题的基本方法,往往具备很强的通用性与普适性.《义务教育数学课程标准(2022年版)》指出,在实际情境中,能够把握研究对象的数学特征,感悟通性通法的数学原理和其中蕴含的数学思想,能够在解决相似的问题中感悟数学的通性、通法.教学中,要尽量挖掘问题解决的最本质、最基本的方法与策略.从本文中的一般化处理结果来看,上述基于图形结构分析而衍生出的15种解题方法都是此类问题的通性通法.
2.注重数学本质,锤炼思维品质
波利亚指出,“掌握数学意味着什么呢?就是要善于解题”.几何图形结构的分析与探究是一个有目标的、复杂的、高级的心智活动,既可以训练学生的数学思维方法,又可以培养学生创造性的思维能力.数学思维是以数学物象为思维对象,以数学语言及符号为思维载体,并以认识和揭示数学规律为目的的一种思维.教学中,应从题目的目标、内容、结构、特征等方面一题多思、一题多解、一题多变,从不同视角、不同层次加以分析、探索,深入挖掘问题本质,从而培养学生的思维品质.
本文中提供的多种解题方法就是从不同的图形结构特征入手,充分联想、构造而产生的不同解题策略.另外,这些解题方法分块呈现.例如,前9种解题方法都属于由“倍角造半角”的基本策略,这又体现了多解归一的功效.“一题多解,多解归一”是培养学生思维灵活性的好方法,前者从不同角度、用多种方法思考问题,思维呈发散性;后者是发现不同方法中相通的本质,思维呈聚合性.两者结合,方能深入挖掘问题本质,彰显解题教学的魅力,使学生能在不同角度、不同层次、不同情境下重新认识所学的知识,达到举一反三、触类旁通的效果,这样才能充分培养学生的思维能力和创造能力,形成良好的思维习惯,全面提高学生的思维品质.
3.发挥教学机智,放眼长线发展
解题是一门技术活,教学是一门艺术活,解题教学需要借助艺术化的手法将基本的解题技能逐渐渗透给学生.罗增儒教授认为,数学学习中真正发生数学的地方都无一例外地充满着数学解题活动.解题教学中要充分发挥教学机智,努力营造一个勤学、善思的教学环境,增强学生对于数学学习的信心与期待.拿本文举例,对于上述15种解题方法,如何循循善诱?如何引导学生果敢、积极地去思索?这离不开一份好的教学设计,离不开一些好的问题.教师若能设计好教学环节,或许会是一节精彩的课堂.
俗话说得好,放长线,钓大鱼.解题教学中,教师若能放眼学生的长远发展,在平时的常态教学中,适时渗透一些初、高中衔接知识或方法,对于学生尤其是优等生的培养势必起到一定的积极作用,使他们对于以后的学习之路充满无限的期待.前文说到,特殊化与一般化是研究问题的一般路径,若学生能提出或教师能引出:上述特殊化与一般化的结论之间是否具备一致性?换言之,一般化的结论对于特殊化的条件是否仍然适用?这时,教师可以断言:“它们是一致的!等到高中,大家就会学习sin 90°=1,到时就能彻底理解了!”这无一不体现了教师的教学机智.这样的课堂必定是极为出彩的,这样的解题教学对于学生的思维冲击必定是震撼的,这也必定能更加坚定学生学习数学的信念以及对未来无限的向往.

