剖析认知图式·关注建构过程·发展推理能力

李 馨，蒋 翀

（浙江省杭州市拱墅区教育研究院；浙江省杭州市萧山区新桐初级中学）

在区域调研中，笔者发现教师常常采用一题多解的方式进行几何解题教学.在其中一节课上，学生展示了多种解法，教师最后还补充了新的解法，整节课下来，热热闹闹，精彩纷呈，授课教师和听课教师都很满意.然而，课后跟踪测试学生解决同样的问题，结果不尽如人意，无外乎三类：①学生依旧只会自己原本使用的解法；②学生只记住自己认为最简单的解法；③相当比例的学生依旧没能完成解答.于是，课堂变成了教师一个人的精彩.

为了研究火热的课堂和冰冷的结果之间产生强烈反差的原因，笔者继续对学生进行访谈.第①类学生认为：“听懂了部分解法，但是解题时还是用自己的解法最顺手.”第②类学生认为：“我觉得这种解法最简单，其他烦琐的解法听听就可以了.”第③类学生则认为：“那些神一样的构造，我听的时候虽懂，过后实在想不起来了.”

皮亚杰认为，获得知识的唯一途径是连续不断地建构.如果教师在课堂上只是进行浅层次的解法呈现，学生就无法认识这些具体解法之间的联系，从而无法提升数学理解能力.教师需要加强基于学生认知图式的指导.这里所指的图式，是指形成各知识点的稳定的关系模式.

杭州市初中数学核心组的教师曾热火朝天地讨论了一道几何题，按不同的解题思路，共整理出18种解法.笔者以此题为例，剖析各种解法背后的认知图式，谈谈解题教学可以通过怎样的方式，帮助学生发挥学习的主动性，动态地建构知识体系，发展学生的推理能力.

一、原题呈现与分析

题目如图1，在矩形ABCD中，AB＞AD，点E在边AB上，且BE=BC，连接CE，CE=CD，作CF平分∠ECD，与边AD交于点F，直线PQ垂直平分CF，分别与AB，CF，CD交于点P，G，Q.若AD=1，求PD的长.

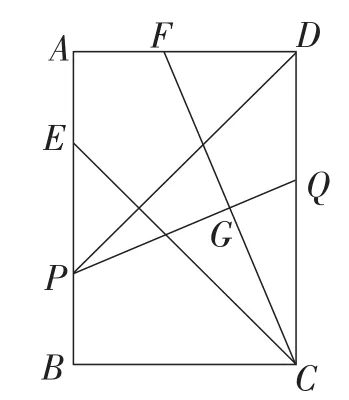
图1

此题拥有丰富的内涵，以矩形为背景，图形中包含了直角三角形、角平分线、线段的垂直平分线等元素.图形略显复杂，但解题难度并不大.学生能够根据问题中的条件获得很多结论，但不易厘清这些结论在实现目标中所起的作用.基于这样的特点，此题是构造、改进、更新学生认知图式的一个很好的素材.

二、通过分类，呈现思维

视角1：借助等腰三角形、角平分线、线段的垂直平分线等结构，根据轴对称图形的性质，利用勾股定理求解.

解法1：如图2，连接EF，PF，PC.

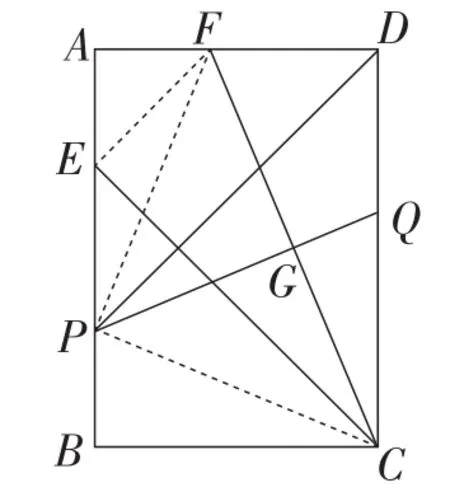
图2

因为CF平分∠ECD，

所以∠ECF=∠DCF.

因为CE=CD，FC=FC，

所以△ECF≌△DCF.

所以∠FEC=∠FDC=90°.

因为BC=BE，∠B=90°，且AD=BC=1，

所以∠AEF=45°，

即△AEF为等腰直角三角形.

因为PQ垂直平分CF，

所以PC=PF.

所以AF2+AP2=PB2+BC2，

所以AP=1.

在此视角下，还可以利用三角形角平分线的性质、相似三角形的性质等求解，部分思路如图3～图6所示，此处不一一赘述.

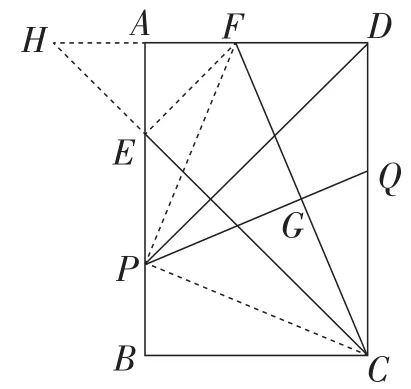
图3

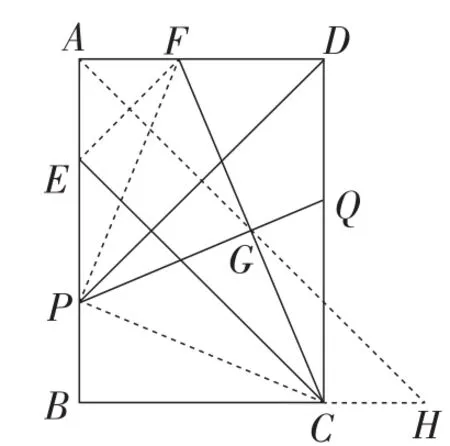
图4

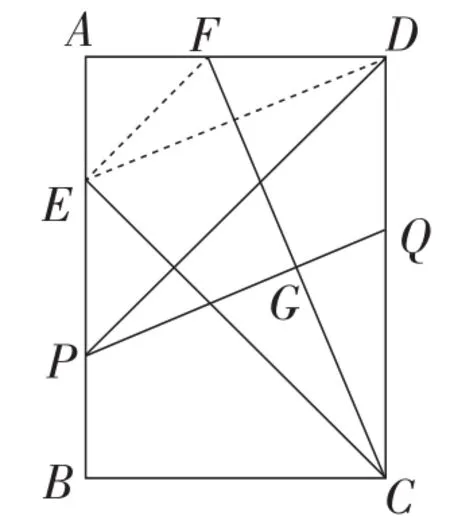
图5

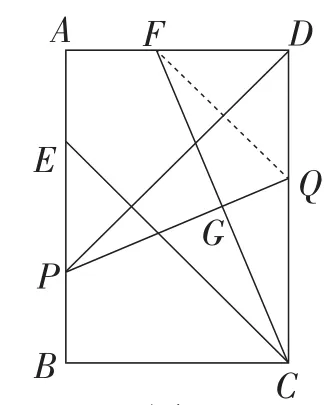
图6

以上均为现阶段学生的各种主流思路和代表解法，一些学有余力的学生可能会从另外角度寻找解决方案.

视角2：巧借辅助圆，利用圆内接四边形的性质求解.

解法2：连接EF.

因为CF平分∠ECD，

所以∠ECF=∠DCF.

因为CE=CD，FC=FC，

所以△ECF≌△DCF.

所以∠FEC=∠FDC=90°.

所以C，D，F，E四点共圆，CF为直径，点G为圆心.

设⊙G与边AB的另一个交点为H，连接HC，HD，HF，如图7所示，则∠FHC=90°.

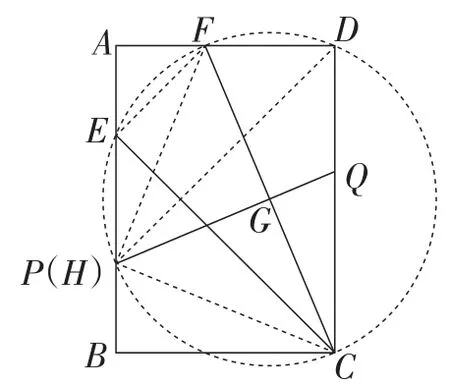
图7

因为BC=BE，∠ABC=90°，

所以∠HFC=∠HEC=45°.

所以HG垂直平分FC.

因为PG垂直平分FC，

所以点H与点P重合.

所以∠DPE=∠DCE=45°.

所以△ADP为等腰直角三角形.

因为AP=1，

辅助圆联系了图形中复杂的对称结构的各要素，从而获得△FPC的特殊性（等腰直角三角形），并进一步借助圆内接四边形的性质实现角的转化，发现△APD是等腰直角三角形，从而解决问题.

视角3：利用锐角三角函数求解.

解法3：如图8，过点P作PH⊥DC于点H，连接FQ.

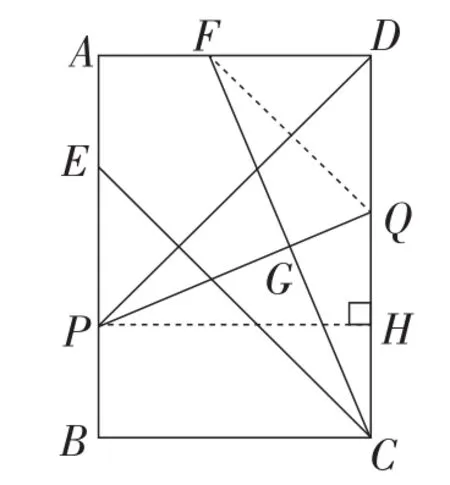
图8

因为BE=BC=1，

所以EC=2，∠ECB=45°.

因为CF平分∠ECD，

所以∠ECF=∠DCF=22.5°.

因为CD=CE=，

所以FD=CD·tan 22.5°=2-.

因为PQ垂直平分CF，

所以FQ=QC.

所以∠FQD=2∠FCQ=45°.

所以DQ=FD=2-.

因为∠PHQ=∠QGC=90°，

所以∠QPH=∠GCQ=22.5°.

所以QH=PH·tan 22.5°=-1.

所以AP=DH=DQ+QH=1.

所以PD=2.

视角4：建立平面直角坐标系，利用代数法求解.

解法4：如图9，以点B为原点建立平面直角坐标系，连接EF.

图9

由题意，得点C的坐标为C（1，0），点F的坐标为

因为直线PQ垂直平分CF，

所以AP=AD=1.

三、剖析图式，重组思维

几何问题的示意图是静态的，但问题的提出是动态的；某种具体的解法是静态的，但解法形成的思路是动态的；多种解法的呈现是静态的，但解法之间的联系是动态的.以动态的视角看条件的推进，每次推进对应了具体解法的思路，由此关注认知图式，并进行深入剖析，有利于学生厘清解法之间的关系，建构知识体系.

1.思路在条件的推进中产生

此题的条件在矩形ABCD的背景下动态有序加强：①CE的长确定了矩形的形状；②角平分线CF确定了点F的位置；③线段FC的垂直平分线PQ确定了点G与点P的位置；④矩形的边AD的长量化了问题，最终确定PD的长度.

学生的不同认知对应了不同的解题思路.由①得，矩形的两条邻边，两条直线CF和PQ的方向决定了可借助22.5°角的三角函数值解决问题.继续由②得，，于是建立平面直角坐标系是一个可行的方案.进一步由③确定了点P的位置，其他通过构造图形解决问题的各种方案均基于此.

2.图式在解法的生成中明晰

我们尝试用图10来展示随着问题条件的推进而产生的解题视角与思路，剖析学生的认知图式并使之可视化.

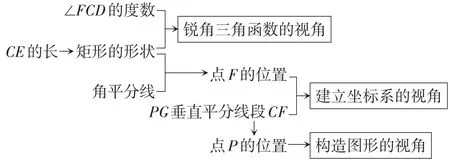
图10

图10表明，各种解决问题的视角在审题过程的不同阶段生成，生成是有顺序的.学习不是简单地感知，被动地接受，而是需要学生自己积极、主动地在行为和心理上构造，通过连续不断的建构得以发展.明晰这个过程后，看一道几何题，有利于串连各种图形结构，在各种视角、思路及解法中找到联系的纽带；看一类具体问题，则提供了如何进行有序思考的方向，可以对解题的认识更深刻，改变思维方式，重构认知图式.

四、精简结构，发展思维

从图10可以清晰地看到，在此题的解法中，除了建立平面直角坐标系、特殊角的锐角三角函数值等代数法，其他所有通过构造图形并利用图形性质求解的方法，最终都聚焦于点P的位置.因此，更新认知图式的关键在于对点P位置特殊性的重新认识.

我们可以通过下面两种方法进行思考，刻画点P在整个图形中的相对位置.

方法1：如图11，连接EF，GE，过点G作GH⊥AB，垂足为点H.

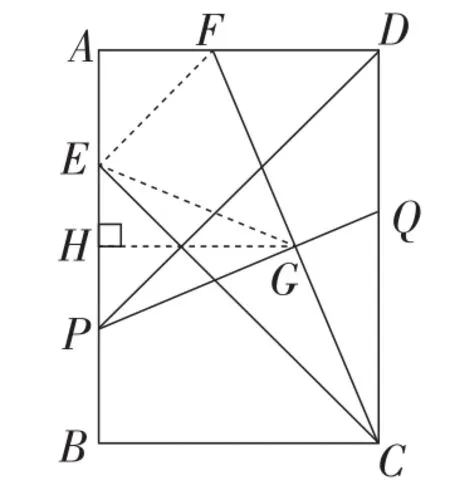
图11

若PD，EC关于GH成轴对称，则

由题意可知，点H是AB的中点，

只需证明HE=HP，即证明GE=GP.

另一方面，∠GEP=∠GEC+∠CEB=67.5°，

又因为∠GPE=∠GQC=90°-∠DCF=67.5°，

所以∠GEP=∠GPE.

所以GE=GP.

方法2：如图12，过点G分别作GH⊥AB，GI⊥AD，垂足分别为点H、点I.

图12

又因为∠GHP=∠GIF=90°，∠HGP=∠FGI，

所以△GHP≌△GIF.

所以AP=HP+AH=1.

在Rt△APD中，AD=AP=1，∠A=90°，

把方法1中的图11简化为图13，方法2中的图12简化为图14，图形的对称性一目了然.图13充分体现了轴对称性，进一步借对称轴GH刻画点P与点E的相对位置；图14则体现了旋转对称性，以点G为旋转中心，进一步刻画点P的位置.

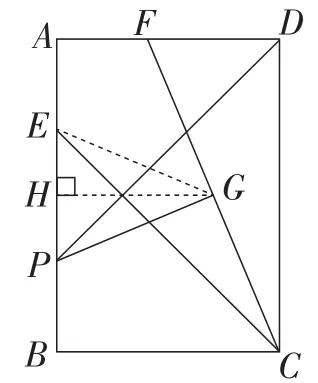
图13

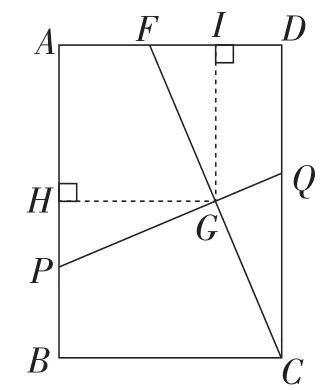
图14

由此，我们看到，这类几何问题的本质是对图形中的点按一定的顺序逐一定位，并定量描述图形中的角度、线段长等，实现对图形中的点的定位.不同的定位顺序呈现出不同的解法，这些显性的解法背后隐藏的是解决问题的不同方法与路径.该题实现解答的最短路径即描述点的位置的顺序是：形→F→G→P.而其他各种图形的构造，无非就是：形→F→G→E→P，形→F→G→Q→P，形→F→G→H→P，都包含了这个最短路径.通过精简图形结构，厘清各种解法之间的关系，并指出寻求最优解的基本方法.

五、反思

最后，谈几点关于几何解题教学的思考.

1.坚持目标导向，抓住解题关键

综观上述解答路径，刻画“点P的位置”是问题解答的关键.在该题的解题教学中，如何帮助学生在复杂的图形中抓住“关键”，并以此为中心，启发学生在认知图式上构建解题路径，成为教师首先要思考和解决的问题.

勾股定理是度量线段长度的工具.图15可以作为启发学生“抓住关键”的过程.由于点P在AB上，其“位置”可由“AP的长”来刻画，由此实现从“数”到“形”的关联与转化.

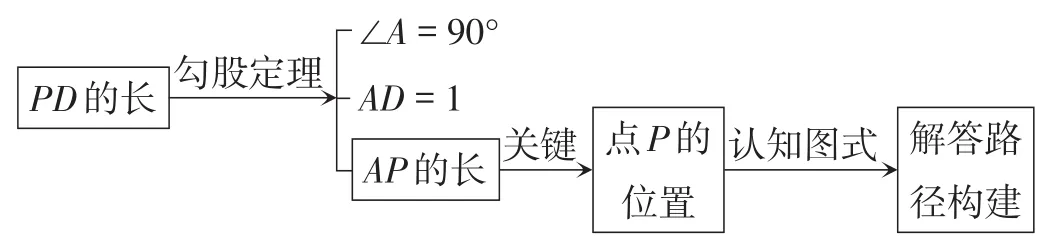
图15

几何解题教学要抓住这样的关键点，使之成为学生从其认知图式出发构建不同解答路径的出发点和归宿，并在目标引领下发现不同路径之间的关联，找到问题的本质.

2.分析确定要素，精简图形结构

根据前面的分析，我们看到“形→F→G→P”是实现解答的最短路径.图16是从确定“点P的位置”的要素进行分析，并将各“要素”位置确定的依赖关系的路径可视化，即点P的位置是由点G的位置所确定的，点G的位置依赖于点F的位置，点F的位置的确定又依赖于矩形的形状（矩形的形状由CE的长，即点E的位置所确定）.由此我们发现，实现解答的最短路径与确定“点P的位置”的各要素之间的依赖关系的路径是一致的.

图16

因此，在教学中引导学生从确定“关键”要素出发探索解题路径，是精简图形结构、实现解答路径最优化的有力工具.从一个“要素”到下一个“要素”的过程，则是教师引导学生基于认知图式构建多视角解答路径的抓手和着力点.

3.借助典例剖析，实现方法迁移

通过前面的分析，我们可以提炼出几何解题教学的一条基本路径，包含两个过程：（1）让学生经历“分析确定要素→提炼关键结构→构建解答路径”的过程，以提升学生分析问题、解决问题的能力；（2）经历“多视角分析比较→发现联系→回归本质”的过程，帮助学生优化认知图式，发展推理能力.

下面以一道中考试题为例，看上述路径是否适用于一般的几何解题教学.

（2020年浙江·杭州卷）如图17，已知AC，BD为⊙O的两条直径，连接AB，BC，OE⊥AB于点E，点F是半径OC的中点，连接EF.

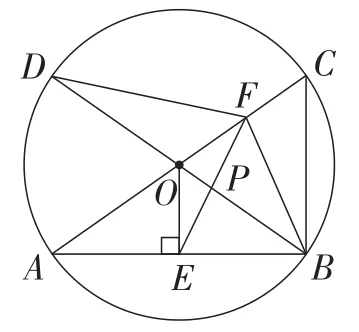
图17

（1）略.

（2）连接BF，DF，设OB与EF交于点P.

①求证：PE=PF.

②略.

解题教学中，教师可以先让学生观察点P的位置、分析确定其位置的要素.由于点P为BO和EF的交点，其位置的决定要素是点E和点F的位置.进一步指导学生根据确定要素，精简结构，提炼出关键图形结构，并将问题简述：如图18，已知，求证：.以此为出发点，引导学生根据自身的认知图式，构建解答问题的不同路径；在不同视角（如图19）的解答路径的比较中发现关联，回归问题的本质：已知，求证.

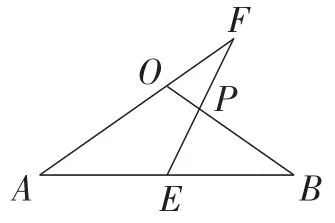
图18

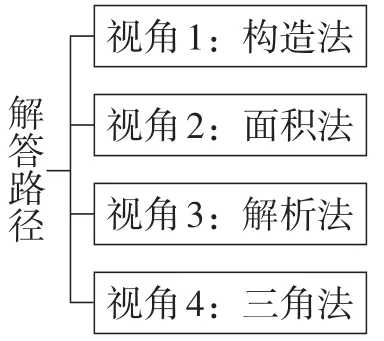
图19

由此可见，上述路径在解决其他几何问题时同样适用，具有一般的指导意义和推广的价值.

不同的认知图式，对应不同的解题方法.几何解题教学的目标就是要在剖析学生原有认知图式的基础上，通过指导学生分析、精简、提炼关键结构，构建、分类、比较解答路径，使学生经历呈现、重组和发展思维的过程，并在这个过程中帮助学生优化认知图式、建构认知体系、发展推理能力，将“冰冷”的解答转化为“火热”的创造.