考虑单元劈裂的流-固耦合连续-非连续方法及定向水力压裂模拟
白雪元, 王学滨, 刘桐辛
(1.辽宁工程技术大学 力学与工程学院,阜新 123000;2.辽宁工程技术大学 计算力学研究所,阜新 123000)
1 引 言
水力压裂过程中,裂缝的扩展受到岩性、射孔角度和地应力等影响[1]。在试验方面,文献[2,3]采用相似材料模型研究了射孔角度对起裂压力和裂缝扩展路径的影响。
目前,水力压裂过程的数值模拟多是基于连续方法进行的。其中,扩展有限元方法适于模拟裂缝扩展,且裂缝扩展不受网格影响。盛茂等[4]采用扩展有限元方法模拟了恒定水压作用下水力裂缝的扩展。赵金洲等[5]采用扩展有限元方法研究了射孔角度对裂缝扩展路径和裂缝面剪应力、切向位移的影响。连续方法相对成熟,已得到广泛应用,但难以处理多条任意分布的裂缝相互作用和大尺度材料的运动问题[6]。
在非连续方法中,Zhang等[7]采用颗粒离散元方法研究了射孔角度对裂缝扩展的影响。在颗粒离散元方法中,颗粒之间存在一定的孔隙。当裂缝扩展时,裂缝与孔隙混在一起,裂缝扩展和流体流动路径并不直观。Jiao等[8]基于非连续变形分析方法构建了水-力耦合模型,模拟了不同射孔角度时岩样的破裂过程。在非连续方法中,尽管可以通过在单元之间加入黏结单元来模拟破裂[9],但通常需引入法向和切向接触刚度,这将对连续介质的应力和应变计算精度产生影响。
为了弥补连续方法和非连续方法的不足,科技人员已发展了一些连续-非连续方法[10-13]。如有限元/离散元方法(FEM/DEM)、连续-非连续单元方法(CDEM)。这些方法适于模拟岩石变形及裂缝扩展过程。在此基础上,科技人员又发展了一些流-固耦合方法[14-16]。如严成增等[14]在FEM/DEM方法中加入了流-固耦合计算模块,提出了一种FDEM-Flow方法。王理想等[15]提出了一种CDEM和中心型有限体积法相结合的流-固耦合方法。
为了更真实地模拟水力压裂过程中的岩石变形、裂缝扩展及流体流动,首先,以可沿四边形单元对角线开裂的拉格朗日元与离散元耦合的连续-非连续方法[17]为基础,引入流体计算模块,发展了一种流-固耦合方法;然后,通过与单裂缝非稳态渗流模型和KGD模型的理论解进行对比,验证了方法的正确性;最后,研究了射孔角度及水平应力对裂缝扩展的影响。
2 可沿对角线开裂的流-固耦合方法
在可沿四边形单元对角线开裂的拉格朗日元与离散元耦合方法的基础上,考虑了流体的作用,发展了一种流-固耦合方法。在该方法中,裂缝可沿单元边界和四边形单元对角线扩展;假定流体仅能在裂缝中流动,固体是非渗透的;流体的流动满足立方定律。该方法适于模拟流体作用下裂缝的弯曲扩展,不需要进行网格重构,而且,在不降低时间步长的情况下,在一定程度上降低了网格依赖性。
2.1 连通裂缝网络的构建
欲计算流体在裂缝中的流动,需建立连通裂缝网络。具体构建过程[18]如下。
记当前非连通裂缝(包括新生裂缝与原有非连通裂缝)的集合为M,取M中每一个元素J进行判断,若J与连通裂缝相连,则J为连通裂缝,并删除M中的J元素。
如此循环,直到M中不再有连通的裂缝。若M中有剩余裂缝,则为非连通裂缝。
2.2 流体对固体作用力的计算
假设裂缝、端点、单元和节点之间的关系如 图1 所示,裂缝1和裂缝2为沿单元边界开裂的裂缝;裂缝3为沿对角线开裂的裂缝。为了便于表述和理解,称裂缝两端的流体节点为端点,每个端点对应两个固体节点,如裂缝1包含端点1和端点2,端点1对应节点4和节点10,端点2对应节点5和节点11。对于裂缝1,端点2和端点1之间的压力差为
Δp=p2-p1+ρg(z2-z1)
(1)
式中p1和p2分别为端点1和端点2的流体压力;z1和z2分别为端点1和端点2在重力方向的坐标,端点的坐标为该点对应的两个固体节点坐标的平均;ρ为流体的密度;g为重力加速度。

图1 裂缝、端点、单元和节点之间的关系Fig.1 Relationship among cracks,endpoints,elements and nodes
根据立方定律,由端点1流入端点2的流量q为[19]
(2)
fs=s2(3-2s)
(0≤s≤1) (3)
式中s为端点的饱和度,k为裂缝的渗透系数,k=1/(12μ),μ为流体动力黏度;L为端点1和端点2之间的距离,即裂缝长度;a为裂缝张开度,取裂缝两端张开度的平均值;fs为端点处与s有关的系数,fs 1和fs 2用于防止两端点之间无压力差时因重力产生的不合理流量,下标1和下标2分别代表端点1和端点2。在计算渗流时,a需大于0,所以,需设定裂缝最小张开度amin,当a 由于端点2不仅与裂缝1相连,还与裂缝2和裂缝3相连。这样,可求得端点2的总流量Q=q1+q2+q3。当前时步端点2的流体压力p为 (4a) (4b,4c) 式中p0为上一时步的流体压力,K为流体的体积模量,V和V0分别为当前时步和上一时步端点的体积,其为与端点相连裂缝体积之和的一半。 图2 流体对单元作用力的施加Fig.2 Application of the fluid pressure on elements 若式(4a)计算的流体压力为负,则说明端点的流体不足。此时,将流体压力设为0,并更新端点的饱和度为 (5) 式中s0为上一时步端点的饱和度。当s<1时,根据式(5)更新端点的饱和度。当s>1时,s=1。 对于一个裂缝(图2),计算出两端点的流体压力后,可确定作用于单元边界的线性分布力,再将单元边界一半的线性分布力等效到相应单元节点上以获得流体对相应单元节点的作用力。若端点A和端点B的流体压力分别为PA和PB,则与端点A对应的单元节点3和单元节点5受到的流体作用力为 FA=(3PA/4+PB/4)×(L/2) (6a) 与端点B对应的单元节点4和单元节点6受到的流体作用力为 FB=(PA/4+3PB/4)×(L/2) (6b) 若一个端点周围有多个裂缝,则需将各裂缝中流体对固体节点的作用力累加以获得流体对单元节点总的作用力。作用力的方向与裂缝角平分线方向(两端点连线方向)垂直,并指向单元。 模型(图3中插图)长W=1 m,宽H=0.1 m,剖分成100×10个正方形单元。模型中含有宽度为5×10-5m的裂缝。模型的上下两个端面均为法向约束,在裂缝左端施加PL=9.5 MPa的流体压力,裂缝右端为无渗透边界。 参数包括固体参数和流体参数。固体一直处于弹性状态,参数取值如下,面密度取为2400 kg/m2,弹性模量取为50 GPa,泊松比取为0.2,局部自适应阻尼系数取为0.2。流体参数取值如下,μ=1×10-3Pa·s,K=20 MPa。时间步长Δt取为 5×10-7s。计算在平面应变和大变形条件下进行,不计重力。为了与理论解对比,在计算时,裂缝宽度保持不变。这样,流体对固体的作用力将不受固体参数的影响。 图3 不同时刻裂缝中流体压力分布Fig.3 Distribution of the fluid pressure in the fracture at different time 图3给出了不同时间t时裂缝中流体压力的理论解[14]和数值解。可以看出,同一时刻,自左向右流体压力逐渐减小;随着t的增加,同一位置的流体压力增加,最终将达到PL。数值解与理论解吻合较好,这在一定程度上验证了方法的正确性。 KGD模型(图4(a)中插图)包括如下假定,(1) 裂缝高度固定;(2) 平面应变; (3) 裂缝内流体的流动符合光滑平板流。 图4 射孔尖端处裂缝张开度和裂缝半长随时间的变化Fig.4 Variation of the fracture opening displacement at the perforation tip and half fracture length with time 模型尺寸为1 m×1 m,剖分成100×100个正方形单元,四个端面均为法向约束。在模型左侧中间位置预置了射孔,射孔长度为0.05 m,向射孔中注入流体的流量q0取为5×10-6m2/s。Δt取为 1×10-6s,其他计算参数取值列入表1。计算在平面应变和大变形条件下进行,不计重力。 图4给出了射孔尖端处裂缝张开度和裂缝半长随时间变化的数值解和理论解[15](图4(b)中插图为t=0.3 s和0.6 s时的垂直位移分布)。其中,裂缝半长不包含射孔的长度,从射孔尖端位置起裂开始计时。可以看出,随着t的增加,裂缝半长增加;射孔尖端处裂缝张开度呈先快后慢增长。数值解与理论结果吻合较好,这进一步验证了方法的正确性。 表1 KGD模型的部分计算参数Tab.1 Some calculation parameters of the KGD model 定向射孔水力压裂模型如图5所示。模型尺寸为0.3 m×0.3 m,圆孔直径为0.02 m。为了便于对比,模型均剖分为5695个四边形单元。在模型中预置射孔,长度约为0.03 m,射孔角度(射孔与x方向的夹角)为β。 图5 定向射孔水力压裂模型Fig.5 Hydraulic fracturing model containing directional perforations 在模型的左侧面和上端面分别施加x方向水平应力σx和y方向水平应力σy=2 MPa,在模型的右侧面和下端面施加法向约束。Δt取为1×10-7s,amin=2×10-5m,其他计算参数取值列入表2。计算在平面应变和大变形条件下进行,不计重力。 表2 水力压裂模型部分计算参数Tab.2 Some calculation parameters of the hydraulic fracturing model (1) 施加载荷和约束后进行计算,直至静力平衡。此步骤共用4000个时步。 (2) 向射孔中注入流体,q0取为5×10-4m2/s,进行计算。 为了研究β和σx的影响。共设计了7个计算方案。方案1~方案4的β分别为0°,30°,50°和70°,σx=2.5 MPa;方案5~方案7的σx分别为 1.5 MPa,2 MPa和3 MPa,β=50°。为了获得破裂压力,监测了射孔靠近圆孔位置处(图5)的流体压力。 图6给出了方案3的最大主应力及裂缝时空分布,应当指出,本文压裂生成的裂缝均为拉裂缝,简称为裂缝;黑色线段表示裂缝(包括预置的裂缝和压裂后生成的裂缝);圆点表示预置射孔尖端。可以看出,裂缝从预置射孔的尖端起裂,呈弯曲状向模型内部扩展,扩展方向逐渐趋于最小主应力方向。在裂缝扩展过程中,最大主应力始终集中在裂缝尖端,裂缝附近会出现一些次生裂缝,但不影响主裂缝的扩展。 图6 方案3的最大主应力及裂缝时空分布(单位:Pa)Fig.6 Spatiotemporal distribution of the maximum principal stress and fractures in scheme 3 (unit:Pa) 图7给出了不同β时流体压力的时空分布(数字表示方案编号)。可以看出,当β不同时,裂缝均从射孔尖端起裂;β对裂缝初始扩展有明显影响,β越大,裂缝发生转向越明显,转向距离越大;裂缝最终总是偏向最小主应力方向扩展。这与文献[2]通过实验获得的β对裂缝扩展的影响规律一致。在射孔附近,流体压力最大;距离射孔越远,流体压力越小。随着时步数目的增加,裂缝中流体压力降低,这与裂缝宽度增加有关。 图8给出了不同β时监测位置处流体压力及裂缝区段数目随时步数目的变化。应当指出,裂缝区段是指两个单元之间的一段裂缝,多个裂缝区段依次相连形成裂缝。 从图8(a)可以看出,随着β的增加,射孔尖端起裂时,监测位置的压力呈增加趋势;当裂缝扩展时,射孔位置处的压力增加,这意味着压裂难度增加。因此,在压裂时,β与最小主应力方向更接近有利于降低压裂成本,提高压裂效率,这与常识相符。随着时步数目的增加,裂缝中流体压力降低,这与图7的流体压力云图结果一致。 从图8(b)可以看出,随着时步数目的增加,不同β时,裂缝区段数目的增速由快变慢,这说明裂缝扩展的速度逐渐变慢。这是由于随着时间的增加,裂缝的体积增加变快,而流体注入的流量是恒定的,这使得裂缝中流体压力逐渐降低,裂缝扩展变慢。方案1~方案3的裂缝区段数目-时步数目曲线相近,而方案4的裂缝区段-时步数目曲线偏高。 图9给出了不同σx时裂缝的时空分布。可以看出,两个方向的水平应力之差越大,裂缝偏转距离越小。如方案7的两个水平应力之差大于方案3,而方案7的裂缝偏转距离小于方案3。 图10给出了不同σx时流体压力分布(时步数目=100000)。可以看出,随着σx的增加,流体压力的最大值增加。 图7 不同β时裂缝中流体压力时空分布(单位:Pa)Fig.7 Spatiotemporal distribution of the fluid pressure in fractures for different β (unit:Pa) 图8 不同β时监测位置处流体压力及裂缝区段数目随时步数目的变化Fig.8 Variation of the fluid pressure at the monitored position and the number of fracture segments with timesteps for different β 图9 不同σx时裂缝的时空分布Fig.9 Spatiotemporal distribution of fractures under different σx 图10 不同σx时裂缝中流体压力分布(时步数目=100000)Fig.10 Distribution of the fluid pressure in fractures under different σx (timestep=100000) 图11给出了不同σx时监测位置处流体压力及裂缝区段数目随时步数目的变化规律。可以看出,随着σx的增加,起裂压力增加,裂缝扩展过程中监测位置处的流体压力增加(图11(a)),也就是说,裂缝扩展时的压裂难度增加。这与图10的流体压力云图结果一致。随着时步数目的增加,监测位置处的流体压力降低(图11(a))。随着时步数目的增加,裂缝的扩展速度逐渐变慢(图11(b))。σx对于裂缝区段数目演化规律的影响不明显。 实验模型条件[2]为σx=6 MPa,σy=1 MPa,σz=15 MPa,β=60°。应当指出,模型中含有套筒。据此建立二维模型,Δt取为5×10-8s,套筒面密度取为7800 kg/m2,弹性模量取为200 GPa,泊松比取为0.2,法向接触刚度取为2×1013Pa/m,其他参数取值等均与4.1节相同。 图11 不同σx时监测位置处流体压力及裂缝区段数目随时步数目的变化Fig.11 Variation of the fluid pressure at the monitored position and the number of fracture segments with timesteps under different σx 图12给出了裂缝扩展路径的实验[2]和数值结果。可以看出,两种结果在定性上吻合。由于本文的模拟条件为二维,不能考虑σz的影响,所以,裂缝转向的数值结果与实验结果尚存在一些差别。 图12 裂缝扩展路径的实验和数值结果Fig.12 Experimental and numerical results of fracture propagation paths (1) 发展了一种单元劈裂的流-固耦合方法。在该方法中,裂缝可沿四边形单元对角线和单元边界扩展,流体在裂缝中的流动满足立方定律。该方法适于模拟流体驱动下的裂缝扩展。 (2) 对于定向射孔水力压裂模型,距离射孔越远,流体压力越小。随着时间的增加,裂缝中流体压力降低。随着射孔角度和x方向水平应力的增加,裂缝起裂和扩展过程中的流体压力增加。两个方向的水平应力之差越大,裂缝转向距离越小。 (3) 对于定向射孔水力压裂模型,在裂缝扩展过程中,裂缝区段数目的增速变慢,这与裂缝体积增加变快有关。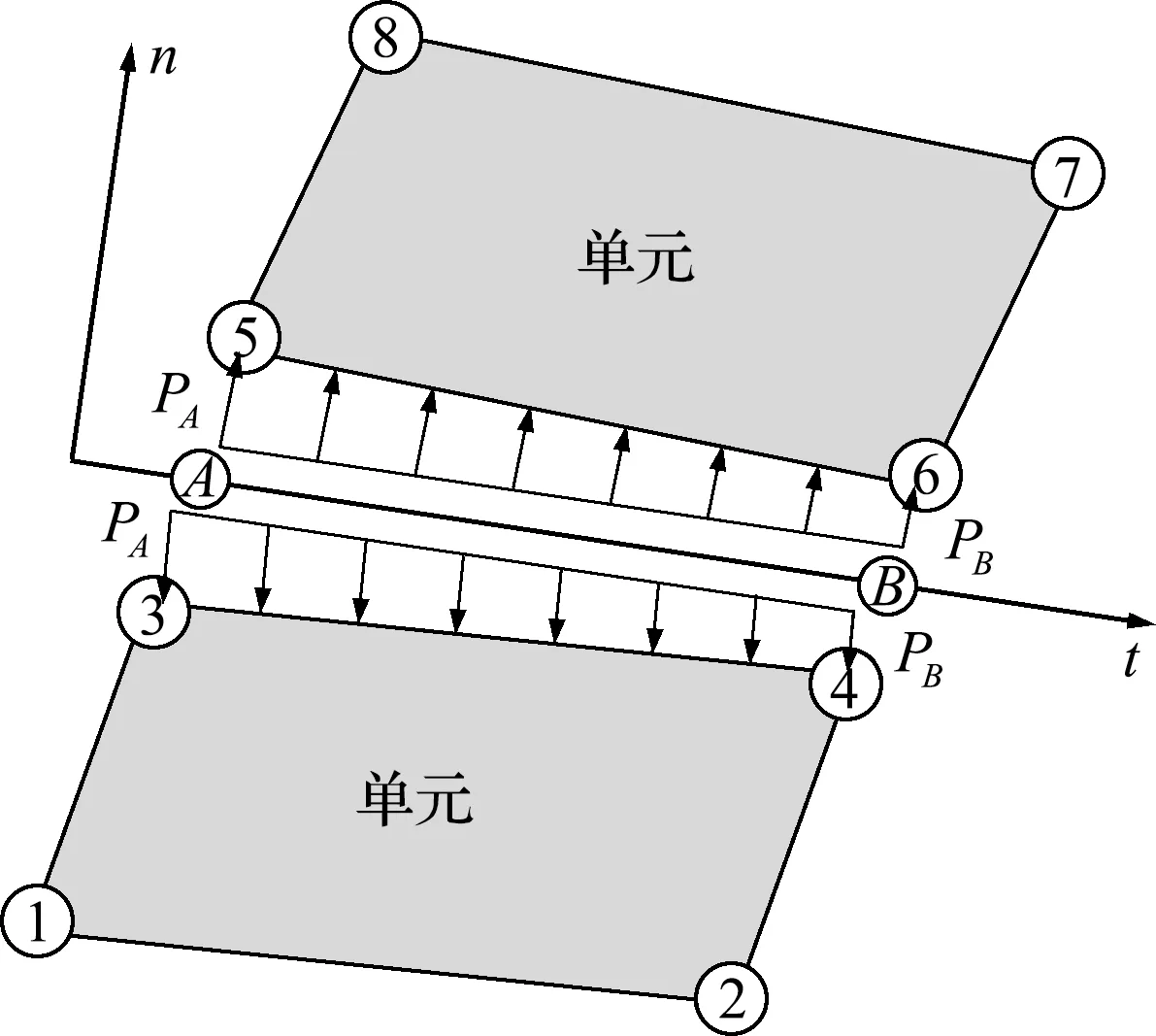
2.3 计算流程
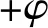
3 方法验证
3.1 单裂缝非稳态渗流模型

3.2 KGD模型
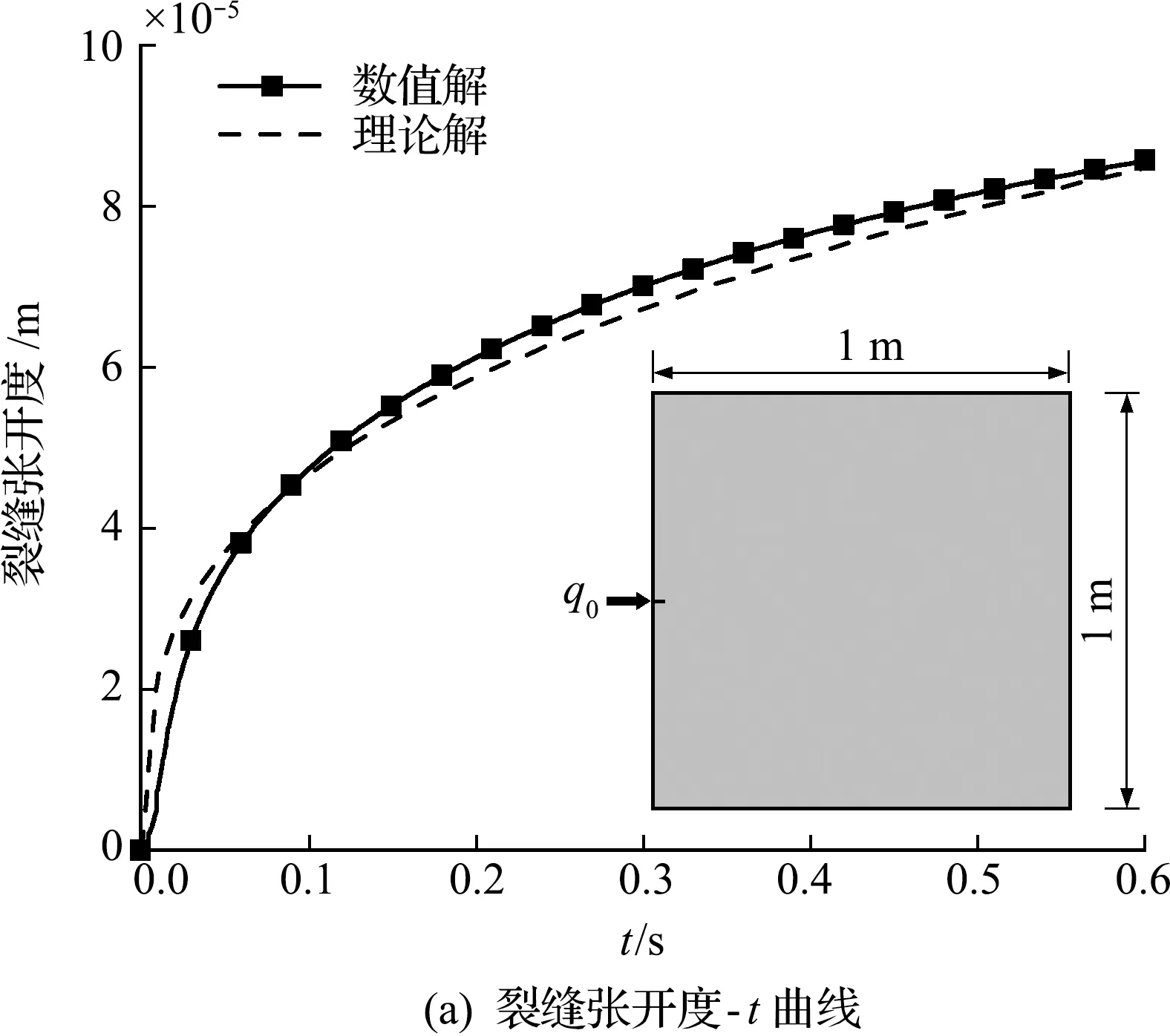
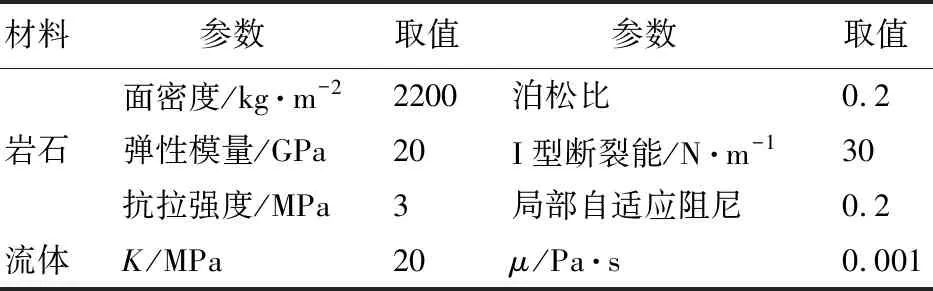
4 射孔角度及水平应力的影响
4.1 模型和参数


4.2 计算步骤和方案
4.3 射孔角度的影响

4.4 σx的影响




4.5 数值与实验结果对比


5 结 论

