基于混合神经网络的汽车运动状态估计*

高振海，温文昊，唐明弘，张 建，陈国迎

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022；2.中国第一汽车集团有限公司智能网联开发院，长春 130000）

前言

汽车主动控制系统与辅助及智能驾驶系统的实现以获取汽车的基本平面运动状态为前提［1-3］，即获取纵向速度、侧向速度与横摆角速度（如图1所示）。一般来说，这些信息可以直接从传感器获取。然而由于传感器精度与成本限制以及量测噪声分布特性难以确定等问题，有些状态信息无法找到有效适用的传感器来直接进行测量或测量精度不高。合理的方法是基于廉价传感器的信息，结合状态估计算法来进行软测量。

传统的运动状态估计算法主要采用基于模型的方法，利用运动学和动力学模型来描述纵侧向速度及横摆角速度与其他车辆参数和状态之间的关系。如卡尔曼滤波（KF）类算法［1］，它将一系列带有噪声的量测结果与基于线性模型的估计结果融合，适用于常规的驾驶条件。扩展卡尔曼滤波（EKF）［4-5］采用非线性车辆模型，估计精度优于KF。无迹卡尔曼滤波（UKF）［6］利用UT变换来避免线性化处理，具有更高的估计精度。

基于模型的估计算法性能取决于车辆建模精度［6］。当车辆运行在大侧偏的工况时，车辆表现出较强的非线性。在这种情况下，线性的车辆模型与实际的车辆系统偏差很大，KF的估计性能显著下降［1，7］。在道路摩擦因数发生改变时，EKF的参数必须进行调整，且EKF只适合于较弱的非线性工况，在较强的非线性工况下其性能会恶化［1，3］。UKF有更高的近似精度但仍受限于模型精度，且成功的UKF估计算法需要精细的参数调整［1，6，8-9］。

机器学习方法尤其是神经网络（NN）近年来有了很大的发展［10］。基于神经网络的方法利用神经网络模型来描述多种廉价传感器信息与估计状态量之间的关系，无需了解车辆的固有参数［11-13］。通过适当的模型结构和丰富多样的训练数据集，这种方法可准确有效地估计车辆运动状态［6-7］。

国内外学者利用深度学习（DL）方法对车辆状态估计进行了大量的研究。Chindamo等［14］使用ANN构建了质心侧偏角的估计算法，并通过CarSim仿真软件来验证估计性能。Ghosh等［15］使用多层长短期记忆网络（LSTM）估计质心侧偏角，其输入包含多个时刻的传感器信号。Spielberg等［16］使用深度神经网络建模高性能车辆的动力学，其输入为前5个时间步长的传感器输入值。结果表明这种建模方法在高附与低附路面下均工作良好。

然而目前大多数的研究直接利用深度学习领域［17］的模型框架，如DNN、LSTM、GRU等［16-19］，未针对车辆运动状态估计问题的特点做出改进。数据集大多来源于同一工况下多次试验采集得到的传感器时序信号，导致在特定数据集下得到的最优网络架构泛化性能较差。在Srinivasan等［18］的研究中，采用的长序列输入GRU网络在未见的工况上性能较差，其原因在于长序列输入的GRU网络很好地记忆了在试验赛道下车辆状态的平均值，而非学习得到车辆的动力学特性。

因此本文提出了一种基于混合神经网络的车辆运动状态估计算法。通过分析车辆本身的动力学基本特性，设计了适合于车辆运动状态估计的HNN混合神经网络架构，实现了车辆运动状态的深度学习估计。在由多工况组成的数据集上对模型进行训练与调优。最后在仿真和实车环境中验证了算法。

1 GRU神经网络工作原理

1.1 GRU神经网络

GRU（gated recurrent unit）神 经 网 络 是RNN（recurrent neural network）网络的一种变体。经典的RNN网络在训练过程中会遇到梯度消失或梯度爆炸的问题。因此新的架构如LSTM（long-short term memory）［20］被发明出来，并被广泛地应用于语言识别、翻译等。

GRU［21］对LSTM进行了简化，通过单个门控单元同时控制遗忘因子和状态更新单元的输出。GRU网络顺序结构如图2所示。图中在时刻t下每一个重复单元的输入量包括样本输入数据x(t)、上一单元的状态h(t-1)，输出量为y(t)。

GRU单元内层级如图3所示，其中，W hr为复位门的状态权重，W xr为复位门的输入权重，b r为复位门的偏置；W hz为更新门的状态权重，W xz为更新门的输入权重，b z为更新门的偏置；W hg为输入门的状态权重，W xg为输入门的输入权重，b g为输入门的偏置；σ(▪)表示sigmoid激活函数，tanh(▪)表示双曲正切激活函数；⊗表示矩阵乘法，⊛表示按元素相乘，⊕表示按元素相加；“1-”表示用1减去所有元素。

在GRU网络中，更新门同时控制遗忘门和输入门。如果更新门的输出是1，则遗忘门打开（=1），输入门关闭（1-1=0）；如果输出0，则相反。下式为更新门计算公式：

复位门控制那些先前状态会被输出给输入门来计算。下式为复位门的计算公式：

输入门的输入量为当前时刻的输入与经过复位门限制之后的前一时刻状态，激活函数为双曲正切函数。下式为输入门的计算公式：

最后的更新公式将前一时刻状态和输入门的输出值用更新门的输出来进行融合。下式为更新公式：

1.2 损失函数与优化方法

由于本文的训练任务为回归任务，损失函数取为均方误差：

式中：h(·)表示混合神经网络正向传播的预测值；表示当前时刻网络的输入；y t表示当前时刻的期望输出值向量；m为样例个数。

采用Adam优化算法来最小化损失函数，它结合了动量优化和RMSProp的思想，跟踪过去梯度的指数衰减平均值与过去平方梯度的指数衰减平均值。算法公式如下：

式中：t代表迭代次数；β1为梯度衰减因子；β2为平方梯度衰减因子；θ为神经网络中的参数；J(▪)代表损失函数。

2 车辆运动状态估计算法设计

运动状态估计网络架构的设计基于对经典车辆动力学模型的分析，以传感器输入信号与估计量之间的主要依赖关系为依据提出了适合于表达这种联系的深度神经网络结构。

2.1 2自由度车辆动力学模型

图4所示为2自由度车辆动力学模型，运动微分方程为

式中：vx为纵向速度；vy为侧向速度；ωr为横摆角速度；δ为前轮转角；k1、k2分别为前后轮侧偏刚度；a、b分别为质心到前后轴距离；m为整车质量；Iz为绕z轴的转动惯量。

该模型可用于描述汽车的基本运动特性。从微分方程组可以看出，当前时刻的侧向速度与横摆角速度值取决于控制输入（前轮转角、纵向速度）和过去时刻两者的状态值，即当前时刻状态值对过去时刻的状态有显式的依赖。

在该模型中纵向速度作为控制输入，而非状态变量。一般来说，当前时刻的纵向速度主要取决于当前时刻的轮速，它们之间为非线性的耦合关系，不具有显式的时序依赖。

2.2 状态估计网络架构设计

基于上述分析可知，纵向速度的估计需要可表达非线性关系的网络结构，而侧向速度与横摆角速度的估计在表达非线性关系的基础上需要显式地表达时序依赖关系。因此本文设计了3层的网络架构来估计车辆的运动状态，分别是传感器输入层，纵向速度估计层，侧向速度与横摆角速度估计层。其连接关系如图5所示。

该算法输入为包括当前时刻在内的前n个时刻的传感器测量值序列。式（13）为t时刻的传感器测量值向量，式中符号定义见表1。输出值为当前时刻t的运动状态向量，包括了纵侧向速度和横摆角速度，如式（14）所示。

2.2.1 传感器输入层

以某国产电动车型CAN总线可获取的传感器测量信号为依据，筛选了与运动状态估计相关的信号作为本算法的传感器输入，总结在表1中。在这些信号中，除传统的基于EKF的估计算法用到的传感器输入外，还包括驱动电机转矩。增加该信号可以使模型得到与纵向相关的特性，提高估计精度。

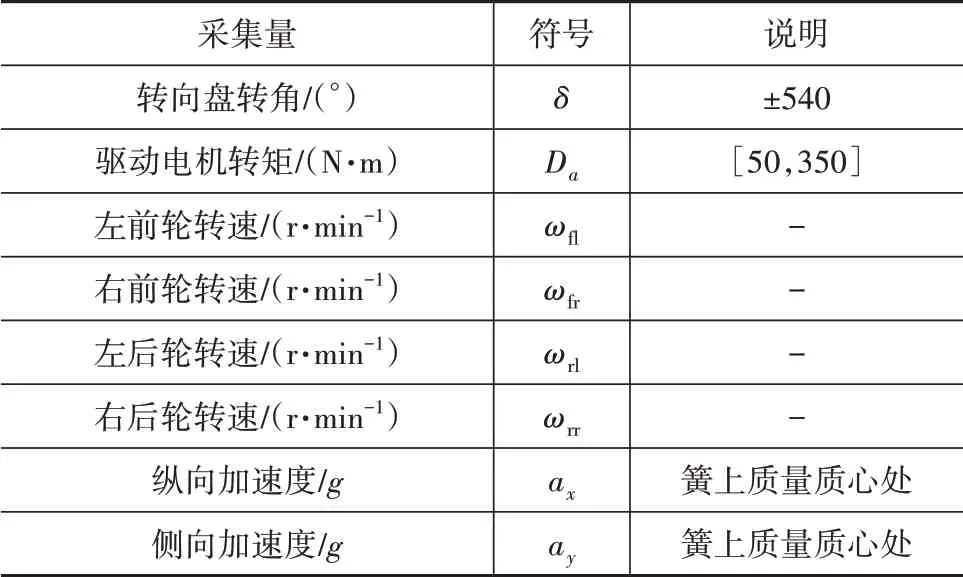
表1 传感器信号输入量

2.2.2 纵向速度估计层

该层基于DNN网络构建，其输入是当前时刻的传感器测量值向量，轮速之外的其他传感器信号可在车辆处于侧滑或纵滑状态下对纵向速度的估计值修正。该网络的隐层数与各隐层的神经元数量作为超参数，在训练过程中确定。

在数据集上训练对比了多种纵向速度估计网络，其结果如表2所示。其中RMSE为均方误差，MAE为平均绝对误差，变化率指相对前者的RMSE与MAE变化幅度，箭头表示相比前者下降。

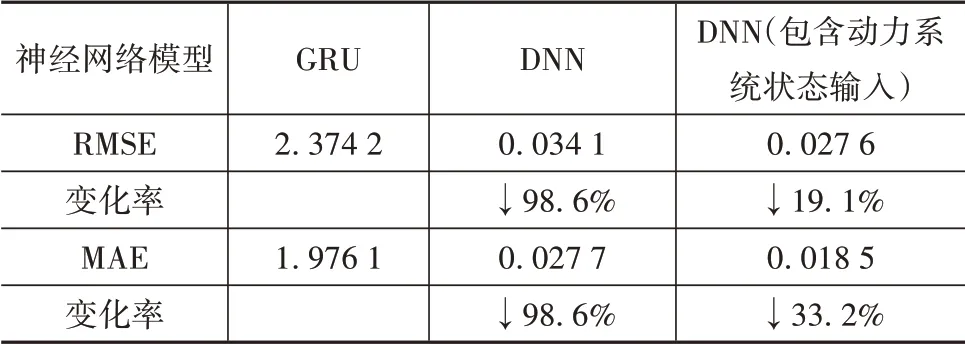
表2 纵向速度估计网络对比

2.2.3 侧向速度与横摆角速度估计层

侧向速度与横摆角速度估计需要的时序依赖关系可以通过RNN类型的网络显式地表达，本方法选用了性能更优的GRU网络。在不同车速条件下，纵向速度的估计值是重要的估计参量，需要将其输入到该层网络中。

该网络单个时刻的输入向量包括传感器测量值向量与纵向速度估计结果vx。前n个时刻的输入组成一个序列作为该网络的输入。GRU网络的单元个数和输入序列的长度n作为超参数在训练时确定，过长的输入序列对于性能的提升不大。在GRU层之后是dropout层，增加该层可以有效地防止GRU网络产生过拟合的现象，同时可提高拟合的精确度。其仅在训练期间使用，在测试与验证过程中将不起作用。最后各GRU单元的输出通过全连接层将维度修正为2。

表3显示了利用不同的网络架构搭建该层时的估计结果。由表3可见，GRU网络的估计精度相比DNN有大幅提升。在输入中包含纵向速度的估计结果后其精度进一步提升。

表3 侧向速度与横摆角速度估计网络对比

3 试验验证与结果分析

为测试验证本文中提出的车辆运动状态估计算法的实际性能，首先在驾驶模拟器中采集了训练数据集，并训练了算法网络模型；然后在仿真环境下的标准工况中对比了本算法与传统算法，并分析讨论了结果；最后在DLC工况下验证算法在实车环境中的性能。

3.1 算法模型训练

3.1.1 数据采集

数据采集应用了驾驶模拟器，其中的车辆模型为前述某国产电动车型，在前期的科研工作中，根据试验数据和模拟数据的差异，通过试错法逐步调整了该模型的参数。选取了5名两年以上驾龄的青年驾驶员，年龄在20-30岁之间。采集过程见图6，每名驾驶员完成一次下述所有工况的数据采集。

数据采集工况包含多种紧急驾驶的典型场景，主要分为纵向和侧向两个部分。侧向工况包括双移线工况、J型转向工况和正弦转向输入工况。每种工况下车速在20-120 km/h范围内变化，间隔为10 km/h。表4为侧向工况的总结。纵向工况包括固定加速踏板开度与加速踏板开度逐渐变化到最大值两种情况，总结在表5中。各工况在不同路面下分别采集。

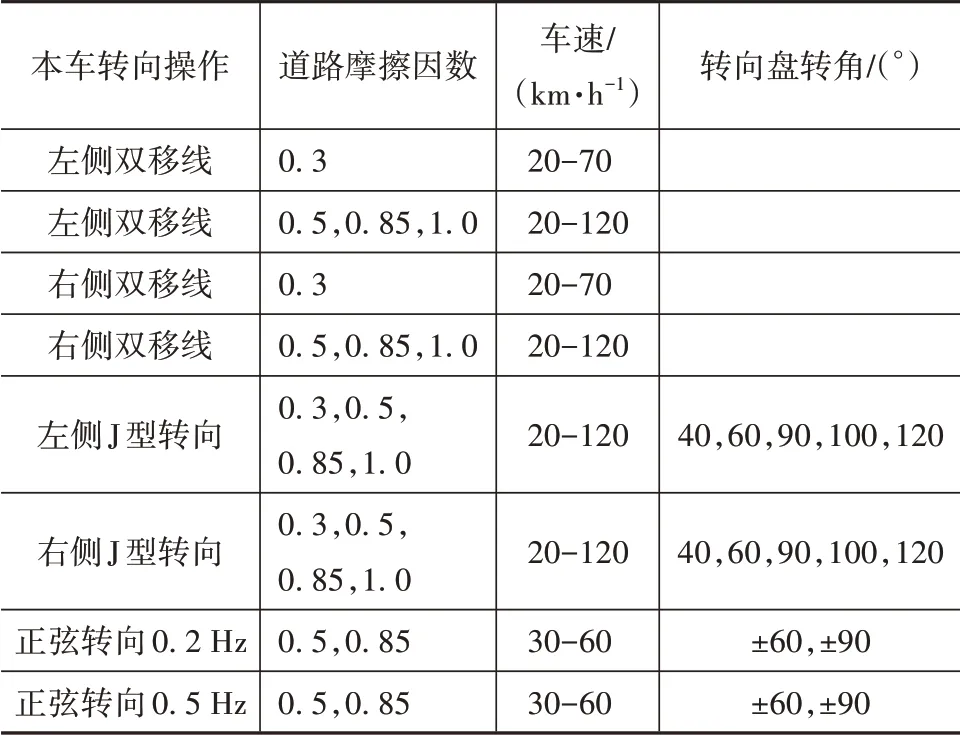
表4 数据集所含侧向工况总结

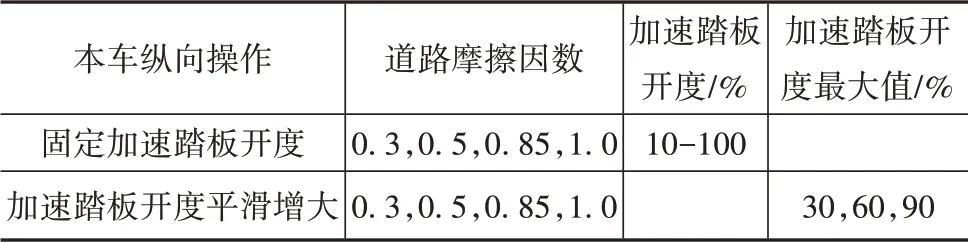
表5 数据集所含纵向工况总结

数据集的有效时长为2 h 1 min 17 s。车辆质心侧偏角真值分布情况如图7所示。由于存在部分纯纵向的工况，因此质心侧偏角在0°附近的数据最多。质心侧偏角在4°以上的数据占整个数据集的31.4%，基本覆盖了常规驾驶工况和大侧偏角工况。此外本数据集在4种路面下的占比分别为17.6%、28.5%、28.5%、25.4%，其分布基本均匀。

3.1.2 混合神经网络训练

训练网络时采用了独立训练的方式，分别训练各子层网络。训练过程为：按照网络的输入输出划分训练样例，得到1 452 673个训练样例；然后划分训练集与验证集；其次搭建网络模型，并在验证集上调优超参数；最后在训练集与验证集上重新训练模型，图8和图9为最后的训练过程。表6和表7展示了经过调优后的超参数设置。

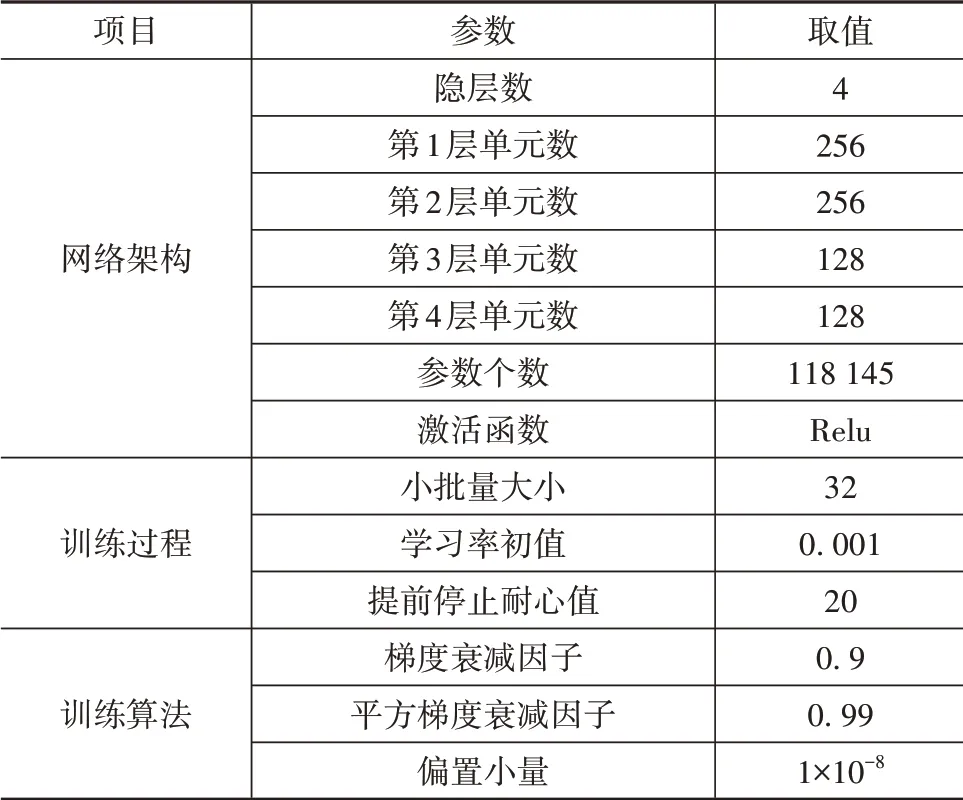
表6 纵向速度估计网络超参数设置

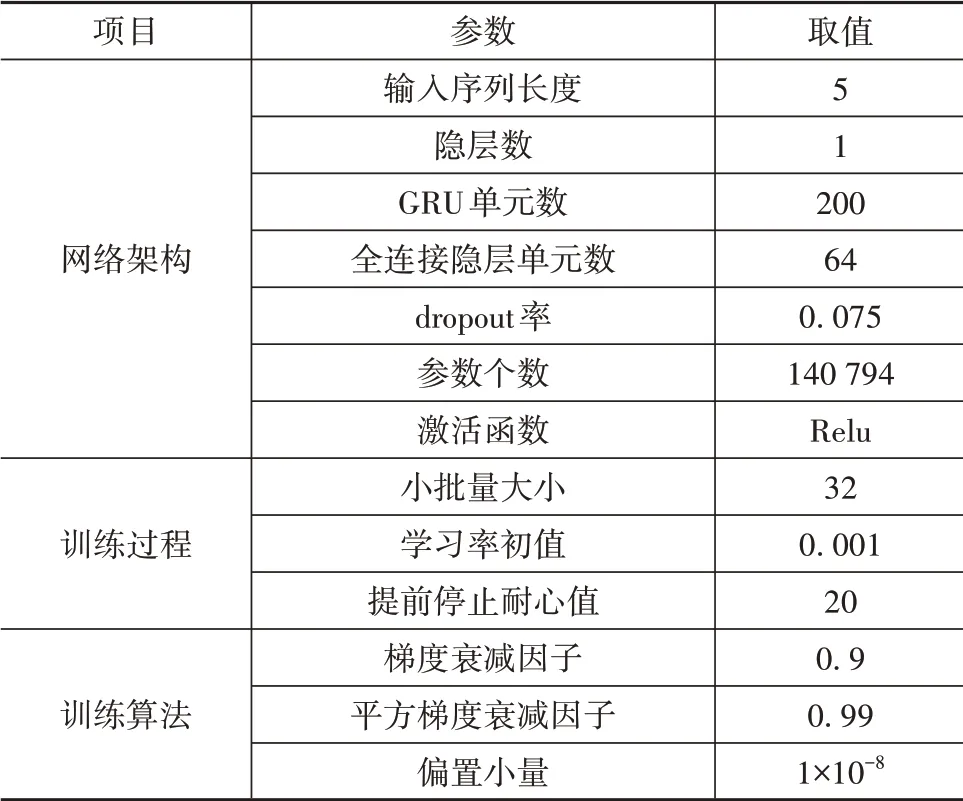
表7 侧向速度与横摆角速度估计网络超参数设置

3.2 仿真测试验证与结果分析

在多种车速与路面条件下测试了本文中提出的运动状态估计算法的性能，与HNN对比的算法总结在表8中。

表8 对比算法

3.2.1 测试工况

测试工况为转向盘转角扫频输入工况。输入频率从0.2增加到0.5 Hz，幅值从±90°降低到±10°，图10为转向盘转角输入曲线。分别在3种路面和4种道路下进行了测试，共计12个测试工况。在高速或低附条件下，该工况某些时刻车辆质心侧偏角可达5°以上，适用于评价大侧偏角情况下的运动状态估计算法性能。

3.2.2 不同车速下的结果分析

在路面摩擦因数为1.0的条件下，对比了不同车速下各模型的估计效果。图11～图13分别为30、70、120 km/h下的估计结果。

当车速为30 km/h时，GRU估计算法在估计纵向速度时其结果的变化趋势与真值显著不同，而侧向速度与横摆角速度估计值的变化趋势与真值一致。EKF算法在估计纵向速度时，出现了较大幅度的波动，另外由于其初值设置问题，导致初始时刻的估计结果存在较大的误差。DNN算法在估计侧向速度时存在明显的负偏置。HNN算法与真值的变化趋势一致。

当车速为70 km/h时，GRU算法、DNN算法与HNN算法的估计结果与30 km/h时一致。EKF算法在估计侧向速度时，出现了相位延后的情况。

当车速为120 km/h时，横摆角速度的真值在波峰与波谷的位置倾向于出现两个极值。这表明随着车速的升高，车辆非线性特性更加明显。EKF算法在估计纵侧向速度时，出现了明显的尖峰，反映出其线性化处理的误差影响变大。GRU网络在估计横摆角速度时其相对误差减少。DNN算法与HNN算法的估计结果与真值的变化趋势一致，HNN算法的误差小于DNN算法。

表9统计了各估计算法在不同车速下对不同状态量预测的均方误差。可以看出HNN的均方误差小于其他算法。

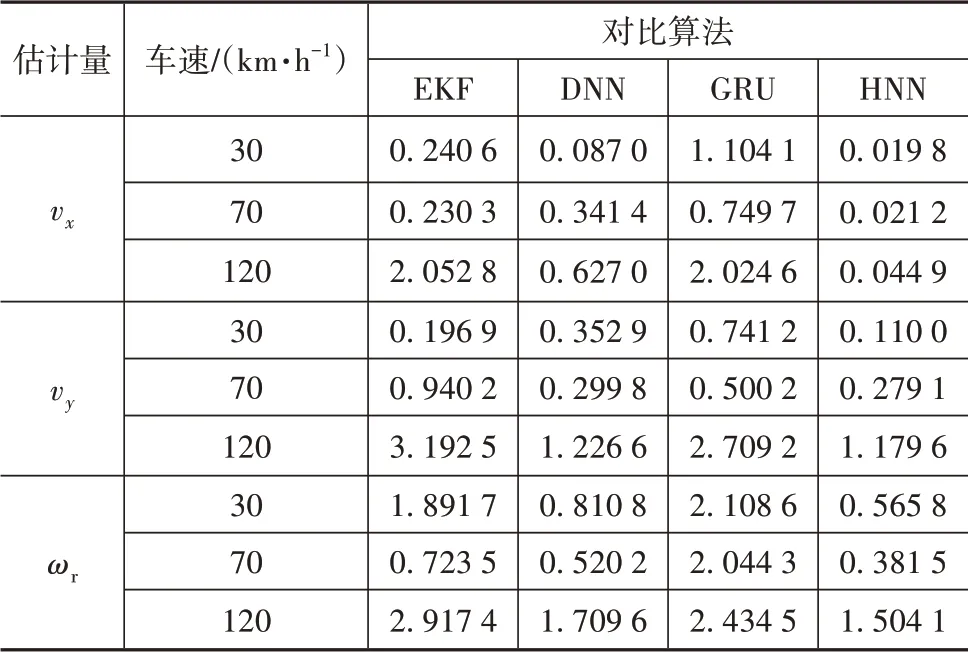
表9 不同车速下各算法估计均方误差RMSE

3.2.3 不同路面下的结果分析

在车速为70 km/h时，对比了不同路面下各个模型的估计效果。图14～图16分别是路面摩擦因数为0.85、0.5、0.3下的估计结果，路面摩擦因数为1.0的估计结果如图12所示。

随着路面摩擦因数的减小，真值的变化趋势明显区别于高附路面。在大转向盘转角输入下，横摆角速度的真值曲线波峰与波谷处倾向于出现两个，而且随着转向盘转角输入幅值的减小，横摆角速度幅值没有明显降低。这表明在低附路面下，车辆出现了滑移。

观察估计结果曲线与表10的均方误差统计结果可以看出，HNN算法在不同路面条件下对不同状态量估计的均方误差最小，且在路面条件变化时，均方误差的变化不明显。在道路摩擦因数降低时，纵向速度估计误差的变化小于0.9%，侧向速度估计误差变化小于17.8%，横摆角速度估计误差变化小于4.9%，远低于EKF算法的估计误差变化。

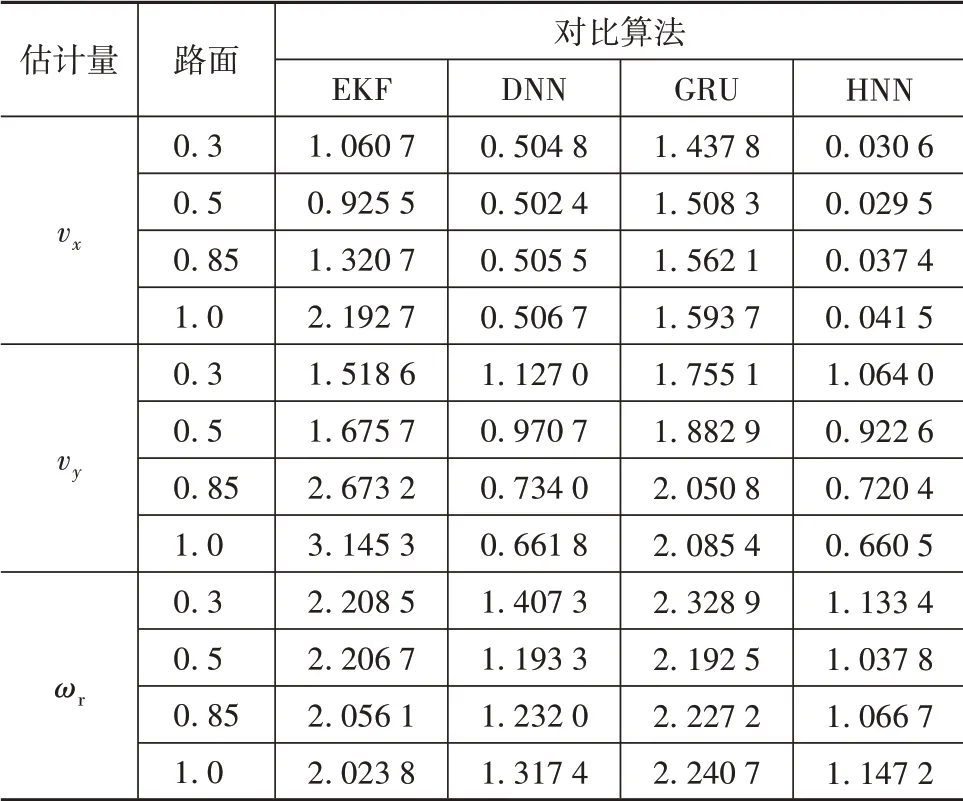
表10 不同路面下各算法估计均方误差RMSE

3.3 实车测试验证与结果分析

3.3.1 实车数据采集

数据采集应用了OxTSRT2500组合导航设备与VECTOR VN1630A CAN采集设备。输入HNN网络的传感器信号来自本车的底盘与动力CAN总线，RT2500获取的本车状态信息作为真值信号。数据采集方案如图17所示。试验在干沥青路面（路面摩擦因数为0.85）下进行。

3.3.2 DLC工况对比

图18为83 km/h车速DLC工况下，EKF算法与HNN算法估计结果的对比。

在纵向速度估计的对比中引入了本车ESP估计的纵向车速。可以看出，在本车横摆角速度出现大幅变化时，实际的纵向车速存在一定的波动。EKF算法估计的结果波动幅度较大，而HNN算法的估计结果很好地贴合了实际车速的变化，而本车ESP的估计结果无法反映出这种波动。

在侧向速度的估计中，EKF算法的估计值偏小，而在横摆角速度的估计中偏大，且存在滞后的现象。HNN算法在侧向速度估计中，精度有所提升，但仍小于真值，而在估计横摆角速度时可以很好地贴合真值的变化。

4 结论

本文中提出了一种基于混合神经网络架构的车辆运动状态估计算法。不同于已有研究直接利用某一神经网络构建算法的方式，本文通过比较不同神经网络的特点，以及车辆本身的动力学特性，设计了适合于车辆运动状态估计任务的HNN神经网络架构。

（1）本算法与基于DNN、GRU的神经网络算法测试对比的结果表明，本方法的特殊设计使得其优于直接利用传统深度学习网络估计的算法。相比于传统的EKF估计方法，HNN估计方法估计精度大幅提高。

（2）HNN估计方法对于道路摩擦因数的变化不敏感，具有一定的鲁棒性。相比基于模型的估计方法可应用于多种路面条件下，扩大了状态估计算法的有效使用范围。

（3）实车测试的结果表明，在驾驶模拟器模拟工况组成的数据集上训练得到的HNN模型通过实车数据的训练可很好地适应实车环境，得到优于EKF算法的估计性能。