基于高效NMPC算法的无人车轨迹跟踪控制研究*

王宏伟，刘晨宇，李 磊，张昊天

（东北大学秦皇岛分校控制工程学院，秦皇岛 066004）

前言

随着无人驾驶技术的快速发展，无人车辆在减少交通事故、提高道路利用率、完成特殊作业、国防军事应用等领域发挥着至关重要的作用［1］。无人车是一个非线性程度高、耦合性强、多输入多输出的系统。其中，无人车轨迹跟踪控制是实现自动驾驶技术的关键，目前已成为国内外学者研究的热点问题，是无人车今后研究的重点方向。

为了克服无人车系统轨迹跟踪控制面临的挑战，提高无人车轨迹跟踪的可靠性、安全性和精确性，国内外学者进行了大量的研究，提出了很多有效的控制方法。主要包括：经典控制［2］、最优化控制［3］、自适应控制［4］、鲁棒控制［5］、滑模控制［6］等。这些控制方法在无人车控制领域取得了明显的效果，但不能解决控制过程中车辆动力学多约束问题。模型预测控制（model predictive control，MPC）可以将无人车系统实际约束条件加入预测运动中，同时根据无人车状态反馈量做出实时调整，达到最优控制。但MPC控制算法在滚动优化时需要对车辆模型线性化，不能准确建立车辆系统精准的非线性模型，容易造成模型失配问题［7］。其次MPC控制算法的约束条件通常被描述为优化过程的硬约束，在极端工况下会增加系统计算负担，导致无法实时求出可行解。

非线性模型预测控制（nonlinear model predictive control，NMPC）对非线性模型具有良好的控制性能，并且可以显式处理系统约束，解决非凸规划问题［8］。在NMPC的设计中，非线性系统会带来繁重的计算负担，高计算负荷和实时求解之间会产生冲突，计算效率是需要考虑的关键因素。文献［9］中对车辆建立轮胎的高度非线性模型，利用序列二次规划（sequential quadratic programming，SQP）算法求解NMPC控制问题，将一部分在线计算负担转移到离线过程。文献［10］中提出了一种FP-SQP改进方法，用以解决非线性问题，但是该算法仅适用于多项式非线性系统，存在一定的局限性。文献［11］中将MPC优化问题分为离线和在线两部分，其中优化仅在在线部分进行，用来减少计算时间。但这种方法的有效性取决于约束问题的可分性，不适合灵活应用于不同场合。文献［12］中提出基于直接多次打靶法的实时迭代算法，将计算时间大幅减少到每次迭代20 ms，但要求代价函数和约束至少两次连续可微。文献［13］中对打靶法的约束条件进行了改进，但只适用于约束都能转换为特定形式，并满足所有最优化条件的场合，这会影响其进一步推广和使用。文献［14］中针对车辆在低速运行工况下，利用遗传算法优化求解过程，实现了NMPC控制器的实时寻优，进一步提升了计算效率。文献［15］中针对车辆轮胎在路径跟踪中存在的高度非线性问题，提出一种线性时变MPC控制器来解决非线性问题的方法。为了减少计算工作量，对非线性模型在初始状态下通过泰勒展开进行线性化，但由于模型近似而导致一定误差。文献［16］中利用粒子群优化算法和现场可编程门阵列芯片的并行计算优势，开发了实时NMPC策略，但芯片成本较高，难以实现大规模应用。文献［17］中提出一种效果与NMPC类似的显式MPC算法，控制问题采用离线优化，并生成在线采用的查找表。这样控制的性能依赖于查找表中定义的大量点，因此导致高内存需求，从而限制了其适用性。与上述求解NMPC的算法相比，连续/广义最小残差算法（continuation/generalized minimal residual，C/GMRES）结合了连续法［18］和Krylov子空间法［19］，在不依赖于求解问题直接优化方法所需的大量迭代的前提下，得到系统最优控制规律，已经发展成为一种普遍求解NMPC的算法［20］。文献［21］在利用NMPC方法研究车辆偏航稳定性时，在C/GMRES算法中引入了死区惩罚函数用于处理不等式约束，实现理想的轨迹跟踪效果。但该算法求解的NMPC设计性能指标中不包括无人车系统终端状态约束，计算出的NMPC控制缺乏稳定性保证。

本文中关注的非线性问题主要为两方面：一是在路面附着系数较低和车速较高情况下，车辆的轮胎模型非线性程度明显增加；二是在求解过程中，因为巨大的计算量出现无可行解或极端解，造成非线性程度增加。针对以上问题提出一种改进的连续/广义最小残差算法（improved continuation/generalized minimal residual，improved-C/GMRES）的NMPC无人车轨迹跟踪控制方法。首先，建立车辆非线性模型并在性能指标中加入多约束条件。然后，为提高求解平滑性，利用障碍罚函数法处理不等式约束，引入连续增加的惩罚因子降低运算负担，提高数值求解的计算效率。最后，通过Simulink和CarSim的联合仿真，验证了无人车在高速和复杂工况条件下所提出算法结果的有效性和准确性，实现精确稳定的轨迹跟踪控制。

1 非线性车辆模型

1.1 动力学模型

为实现轨迹跟踪控制，对车辆横向和纵向建立2自由度车辆模型，定义XOY为大地坐标系，并且设为惯性参考系。定义xoy为车辆坐标系，其中原点o为车辆质心。

建立2自由度动力学模型如图1所示。

图中：X和Y分别为车辆横、纵坐标；vx为纵向速度；vy为横向速度；β为质心侧偏角；γ为横摆角速度；φ为航向角；Lf和Lr分别为质心到前、后轴的距离；Fyf和Fyr分别为前、后轮胎的侧向力；αf和αr分别为前、后轮轮胎侧偏角；δ为车辆前轮转角。

车辆坐标(X，Y)与行驶速度的关系为

根据图1可以得到车辆的动力学方程：

式中Iz为绕z轴的转动惯量。

车辆轮胎在前/后轮受到的侧向力为

式中Fyfl、Fyfr、Fyrl和Fyrr分别为左前轮、右前轮、左后轮和右后轮受到的侧向力。

当质心侧偏角很小的时候，tanβ≈β，由几何关系可得：

建立的轨迹跟踪示意图如图2所示。

图中：φr为期望轨迹的参考航向角；φ为实际轨迹的航向角。

定义ey表示车辆位置和期望路径之间的距离误差，实际意义为从车辆质心o到期望轨迹上正交投影点T的距离。定义eφ为航向角误差，eφ=φ-φr，可以得到公式：

1.2 轮胎模型

轮胎在高速行驶的过程中，非线性特性会尤为明显，直接影响车辆的稳定性和操纵性。

前、后轮轮胎侧偏角计算公式为

魔术轮胎（magic formula，MF）模型对车辆轮胎力非线性特性拟合较好，其表达式为

式中：α为轮胎侧偏角；μ为路面附着系数；FZ为轮胎垂直载荷；B为刚度系数；CFα为转弯刚度；C为轮胎模型形状因子；D为轮胎模型峰值因子；E为轮胎模型曲率因子；k1和k2分别为辨识系数。

将式（2）～式（8）代入式（1），得到车辆的偏航运动方程：

式中Fzf和Fzr分别为前、后轮胎垂直载荷。

2 NMPC控制器设计

NMPC对于求解车辆运动过程的非线性问题有着较好的计算速度和计算精度。本文对设计的性能指标函数添加非线性软约束和硬约束条件，在保证车辆行驶稳定性的前提下，同时提高对目标路径的跟踪性能。

2.1 预测模型

根据式（1）-式（6），得到非线性模型预测的状态空间表达式，即

式中：f为系统的状态方程；x=[β，γ，ey，eφ，X，Y]为系统状态量；u=δ为控制变量；ω=φr为外部干扰；y为系统输出方程；ξ为受控变量。

2.2 问题描述

NMPC控制性能指标函数最小化可表示为

式中：x0为车辆的初始状态；t为初始采样时间；T为系统的预测时域；τ为最小化预测时域。

式（12）第1式等式右侧第1项为系统的终端状态，第2项可以表示为

式中：xτ为τ时刻的实际轨迹；x r为期望参考轨迹；Q=diag{q1，…，q6}和R=diag{r1}为权重系数矩阵，q1～q6和r1为权重系数。

将式（12）简化为如下形式：

式中U为计算得到的不同时刻最优控制序列。

3 求解器设计

利用NMPC求解会使计算量增加，为提高无人车稳定性和求解效率，本文在C/GMRES算法基础上进行改进，得到improved-C/GMRES算法。

3.1 控制规律设计

为了保证NMPC控制器的稳定性，对车辆前轮转角控制设计了辅助控制规律。根据文献［23］采用反步法得到控制规律：

式中：γaux(t)为车辆前轮转角速度控制规律；ka和kb为调整因子。

kb＞vx ka是速度误差和航向角误差收敛为0的必要条件。

构造对应的李雅普诺夫函数：

对于所构造的李雅普诺夫函数，在定义域内是连续可微的，并且是无界的。由李雅普诺夫定理可知，存在一组ϖi(i=1，2，3)满足下列式子：

根据NMPC求解特点，在每个采样时刻输入一个采样周期，只会对非线性模型预测的第一个更新状态具有控制作用，得到以下不等式：

利用李雅普诺夫定理，得到无人车辆系统的终端状态，将终端约束这个附加约束应用到在线优化中，可以证明闭环系统的稳定性。即在优化过程中施加的约束要求系统在预测期结束时的状态相对于预测期开始时的状态在范数上收敛。将设定值选为优化问题中的终端等式约束，既保证渐近收敛到期望轨迹，又保证了NMPC在线求解的优化问题的可行性。

3.2 约束条件

根据车辆实际转向系统，可以得到如式（20）所示的约束条件：

式中：角标max和min分别表示为约束的上、下边界；β和γ的最大值满足式（21）条件。

式中：g为重力加速度；δf∈[-6∘，6∘]。

为提高NMPC控制方法的稳定性，使得到的最优性保证在有限时域下的闭环稳定，对NMPC优化问题增加一个稳定性约束条件：

给定每个时刻的初始状态x(t)，可以根据式（12）求解最优控制序列。由于仅取最优控制序列的第一个元素作为实际控制值，所以仅考虑在预测时间[t，t+τ]中的稳定性约束。

3.3 障碍罚函数

在NMPC求解过程中，求解问题是一个带有不等式约束的非线性规划问题，无法利用常规方法得到解析解。为了解决不等式约束局限，利用障碍罚函数法［23］来计算数值解。

在性能指标函数中引入违反约束惩罚项。定义一个新的理想障碍函数：

由于障碍函数在ζ(c(x(τ)，u(τ)))=0处缺乏连续可微性，导致该函数在实数域上不可微。为解决这个问题，引入近似函数，其表达式为

式中κ为近似系数。当κ→∞时，在c(x(τ)，u(τ))=0处可以用式（24）代替。

在不等式约束中加入障碍函数，既将控制变量限制在合理范围之内，可以遵从约束条件，同时可以兼顾性能指标中最小值条件，保证了性能指标的优越，在多约束条件下新的优化问题可以成功求解，这种方法特别适合于具有多状态约束的无人车系统。此外，这种方法不需要引入额外的优化变量，在保证计算精度的前提下，可以将计算工作量保持在相对较低的水平。

3.4 最优化条件

为了保证NMPC优化问题中车辆的稳定性，加入一个稳定性约束条件，将原来的优化问题改写为

上述轨迹跟踪问题可以等价最优控制必要条件，为解决最优控制问题，本文引入哈密顿函数：

式中λ为共态向量。

基于庞特里亚金最大化原理（Pontryagin’s maximum principle，PMP），无人车轨迹跟踪最优控制问题可以转化为两点边值问题（two-point boundary value problem，TPBVP），将连续的两点边值问题离散化，在预测时域[0，T]内得到离散的两点边值问题为

通过式（27）计算可以得到：

取最优控制的第一个元素(t)作为实际控制输入。为了求解t时刻式（28）矩阵，利用数值延拓法和前向差分广义最小残差（forward-difference generalized minimal residual，FDGMRES）方法。文献［20］和文献［24］中给出了算法的具体描述。该算法避免求解大量的雅可比矩阵、Hessian矩阵和逆矩阵，将这种函数计算方法简写为

式中：ηmax为设置的最大迭代次数；Û为一个特定的初始猜测。

3.5 高效NMPC优化算法

在初始化过程中，首先在传统C/GMRES方法的基础上加入变量参数求解PMP条件，只求解一次得到可行的初始控制输入序列。

基于求解TPBVP的方法，在最优解的邻域中，找到收敛更快且精度更高的解。所以在约束条件下需要找到一组更好的初始控制输入序列U。于是引入连续增加的障碍项权重因子ε求解式（28），并将当前时刻求解的输入序列作为下次迭代的初始值。高效NMPC算法引入连续增加的障碍项权重因子ε，可以通过迭代次数的增加，寻找使代价函数最小的权重因子ε，找到满足条件的最优控制序列，从而减小误差，提高系统的控制精度。

分别利用传统的C/GMRES算法和本文提出improved-C/GMRES算法进行计算求解，通过对比这两种算法的计算结果，验证improved-C/GMRES算法，在保证求解效率的前提下，可以保证无人车轨迹跟踪的稳定性，表1和表2给出这两种算法的具体步骤。

表1 C/GMRES算法

表2 improved-C/GMRES算法

4 仿真与分析

为了验证本文所提出的高效NMPC方法在无人车轨迹跟踪控制的精度和求解速度，基于Simulink和CarSim搭建的联合仿真平台进行仿真分析，在2.3GHz笔记本电脑上的Intel Core i7 8750H CPU下对所提出的策略进行验证，将利用improved-C/GMRES算法求解的高效NMPC与利用C/GMRES求解的NMPC进行对比。

本文选择的复杂路况是在标准的双移线和蛇行工况基础上进行调整，使原有曲线具有更低的路面附着系数和更大的转弯弧度，同时让车辆保持较高的速度通过设计路段，验证算法性能。表3和表4分别表示车辆动力学模型参数和控制器参数。

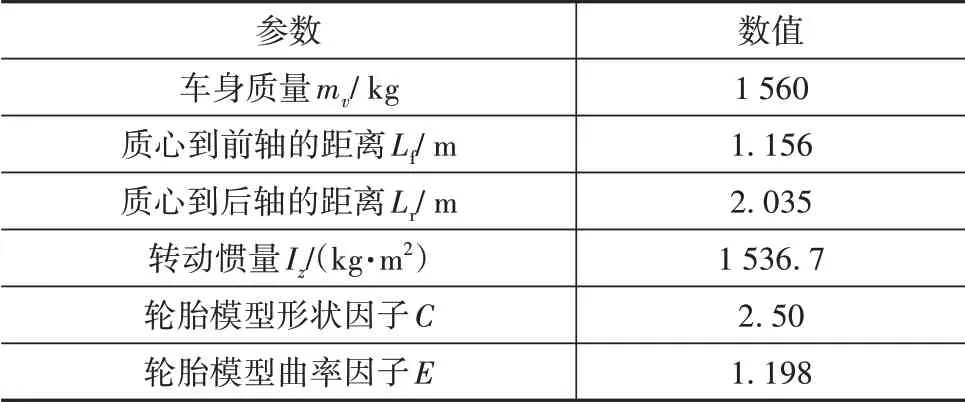
表3 车辆动力学模型参数

表4 控制器参数

4.1 双移线工况仿真

为了验证对比两种算法的控制效果，在双移线工况进行仿真验证。道路附着系数μ为0.6，目标车速为60 km/h，并假设车辆初始状态和偏航角都为零。

图3表示轨迹跟踪曲线图，图4表示轨迹误差曲线图。

由图3和图4可知，标准NMPC控制轨迹误差在±0.15 m之内，在5～6 s之间出现较大的误差波动；而高效NMPC控制轨迹误差在±0.07 m之内，误差更小，在控制过程中未产生剧烈的误差波动。可见高效NMPC控制器在高速条件下跟踪控制效果更好。

图5表示航向角跟随曲线图，图6表示航向角误差曲线图。

由图5和图6可知，标准NMPC控制角度误差较大，在3～4 s和5～6 s之间都出现了明显的角度误差；而高效NMPC控制角度误差更小，且控制过程中角度变化量也更加平缓，没有出现剧烈波动的情况。可见高效NMPC控制器在路面附着系数较低，转弯弧度较大的工况下，可以更精准实现角度跟踪控制，并且可以提高车辆稳定性和安全性。

4.2 蛇行工况仿真

为了进一步验证本文所提方法的精确性和稳定性，在更为复杂的蛇行工况下进行仿真。蛇行工况在短距离内有多个大幅度转弯，道路附着系数μ为0.45，目标车速为60 km/h，并假设车辆初始状态以及偏航角都为零。

图7表示轨迹跟踪曲线图，图8表示轨迹误差曲线图。由图可见，标准NMPC控制轨迹误差在±0.4 m之内，在3～4 s和6～7 s之间出现较大的误差波动；而高效NMPC控制轨迹误差在±0.1 m之内，误差更小且未产生剧烈的误差波动。可见高效NMPC控制器在连续转弯的情况下仍可以保持较好的控制效果。

图9表示航向角跟随曲线图，图10表示航向角误差曲线图。

由图9和图10的对比结果可知，标准NMPC控制角度误差较大，在8～9 s都出现了明显的角度误差，车辆在行驶过程中的稳定性较差；而高效NMPC角度误差较小且较为平缓，在复杂工况下可以保持稳定性。

4.3 计算效率验证

本文在验证两种工况的控制精度时，为了避免实验数据出现偶然性，在路况参数和控制器参数设置相同的条件下分别各进行了50次验证实验，将实验数据的平均误差范围频数次数分别统计到表5和表6中。

由表5和表6的统计数据可知，标准NMPC控制的误差要明显大于高效NMPC控制，高效NMPC控制误差范围更小，控制精度更高。

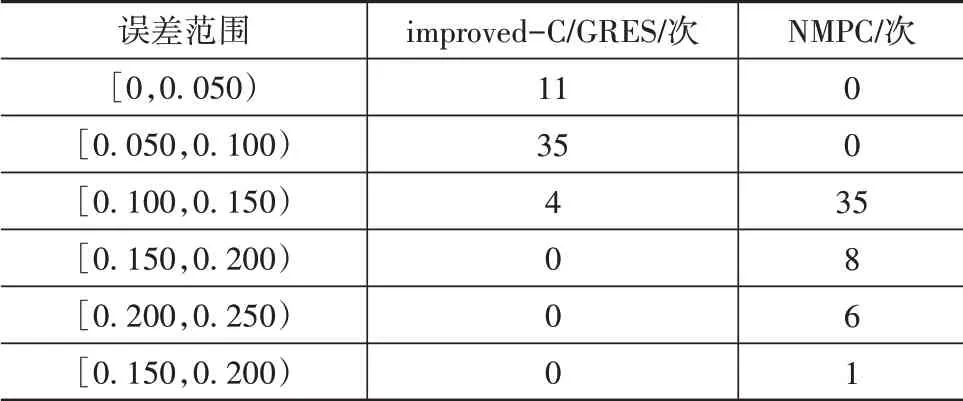
表5 工况1平均跟踪误差频数统计

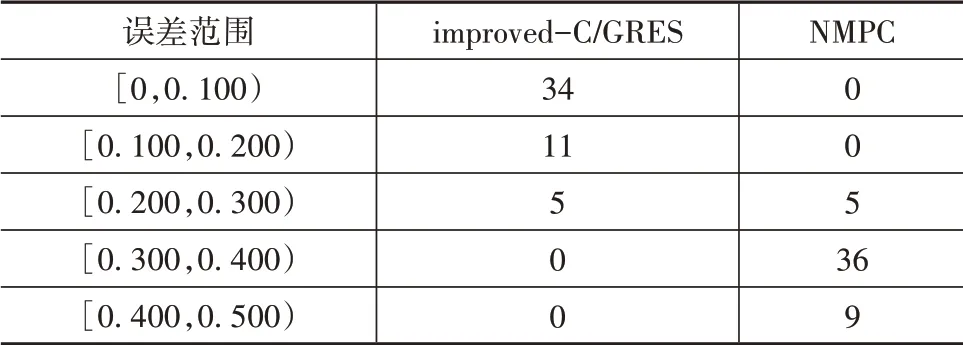
表6 工况2平均跟踪误差频数统计

同时分别统计两种方法的每一步迭代计算所需时间，结果如表7所示。表7中表示在不同工况不同算法的计算耗时情况，表中数据为计算仿真的单次优化平均计算耗时。

由表7的统计数据可知，高效NMPC控制在两种工况下单次优化时间远远低于标准NMPC控制，在工况1和工况2中将计算时间大幅减少到每次迭代18.9和25.6 ms，大大提升了计算效率。

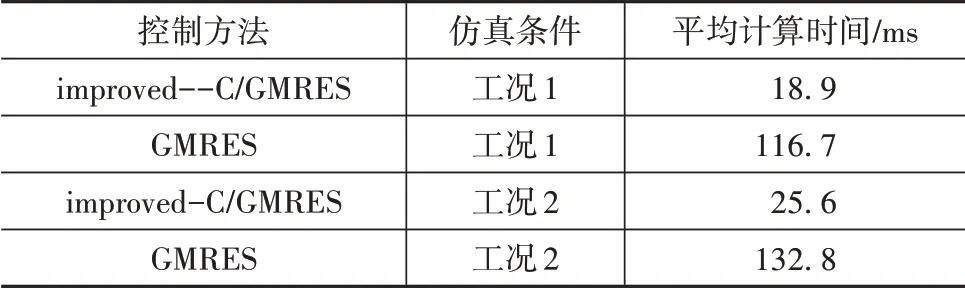
表7 单次优化计算耗时对比表

为了验证本文提出improved-C/GMRES控制算法的高效性，利用两种算法分别完成工况1和工况2的轨迹跟踪，将50次计算模拟时间求取平均值作为最终的仿真时间，两种算法仿真时间如图11所示。从图中可以看出：C/GMRES算法求解上述两种工况所需平均时间分别为1.663和7.921 s；improved-C/GMRES算法所需时间分别为0.353和1.632 s。可见，采用improved-C/GMRES算法求解所需时间远远低于C/GMRES算法的求解时间。表明所提出的NMPC控制器可以实现实时优化，提高计算效率，充分证明improved-C/GMRES算法处理非线性问题的高效性。

5 结论

本文中基于无人车的轨迹跟踪问题设计了一种高效NMPC控制算法。首先建立车辆非线性模型，利用障碍罚函数法处理非线性不等式多约束条件，对原有性能指标进行优化。然后通过引入连续增加的惩罚因子加快数值计算的求解效率。最后通过Simulink和CarSim的联合仿真，在路面附着系数较低，车速较高的两种工况下验证算法的控制效果。结果表明：与C/GMRES算法的NMPC相比，利用improved-C/GMRES算法的高效NMPC在两种工况下轨迹跟踪最大误差大幅度减少，轨迹控制精度得到明显提高；航向角最大误差大幅度减小，稳定性得到明显提高；计算效率提高78.77%和79.40%。improved-C/GMRES控制算法在保证轨迹跟踪精度的同时，使车辆航向角跟踪达到理想的效果，并提高车辆转弯过程的稳定性，可以大幅度提高计算效率，对计算负担大的非线性问题同样可以快速求解，满足无人车实时性要求。