麦克劳林级数展开的教学思考及若干方法

200233 上海市世界外国语中学 朱灵芝

麦克劳林级数是泰勒级数在x=0处的一种特殊形式，它是牛顿的学生麦克劳林在1742年给出的，其用途十分广泛，主要应用于求极限、近似值计算以及证明不等式等方面.多项式函数是学生最熟悉的函数之一，其性质比较简单，因此，对于一些比较复杂的非多项式函数，通常用多项式函数去逼近它，从而研究其性质.鉴于此，DP(Diploma Programme)12年级的数学教学中详细介绍了麦克劳林级数(Maclaurin series).因为麦克劳林级数理论性强又比较抽象,学生学习这部分内容比较困难，很多学生一看到公式就产生畏难情绪，想要放弃，因而在实际教学过程中，学生很难感受到麦克劳林级数化繁为简的重要作用.

一、 麦克劳林级数展开的教学思考

受章建跃博士《如何实现思维的教学》[1]一文的启发，笔者发现从简单到复杂、从直观到抽象是学生学习的基本认知规律.为了让学生对麦克劳林级数的展开有一个直观、清晰、透彻的认识，笔者在麦克劳林级数的课堂教学中发挥了TI-nspire计算器的作用，利用计算器的slider功能，对逼近的过程进行了动画演示.以数形结合的方式让学生亲眼目睹数学知识产生过程，帮助学生理解，力求教学符合学生的认知规律，充分发挥学生的主体意识，加强“数学思维”教学，从课堂实际教学来看,效果不错.

二、 麦克劳林级数展开的若干方法

在课堂实际教学中取得了突破后，笔者分析了学生对麦克劳林级数的畏难情绪，其源头主要是公式太长，学生看到公式后产生畏难情绪，所以如何让麦克劳林级数的求法具有多样性，并能变得“友善”、简单起来，成为下一个突破口.为了使学生不再畏难，使其更好地掌握麦克劳林级数的展开，并能熟练应用，笔者从学生的角度出发，和学生一起通过例题总结麦克劳林级数展开的若干方法.

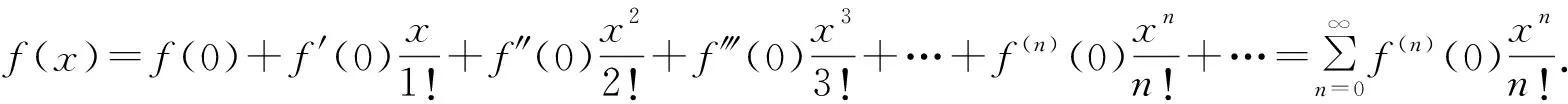
根据比式判别法可以求出其收敛区间为(-1, 1).(过程略)

定义法是揭示麦克劳林级数概念内涵和本质的逻辑方法，是对数学实体的高度抽象.定义法具有普适性，其优越性是所有函数都适用的，但有些函数的求导非常复杂，这也是学生对定义法比较排斥的原因.因此，有必要引导学生思考有没有可代替的方法.在用定义法求出麦克劳林级数后，引导学生逆向思考，定义法求出的麦克劳林级数恰好是学生所熟悉的无穷等比递缩数列，于是产生了方法2.

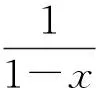
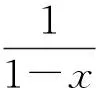
相对于方法2，方法3适用的范围大大拓展，但仍局限于有理函数的范畴，学生对形如 (a+bx)n,n∈Q的形式产生了疑问.学生在DP 10学习了幂为自然数的二项式定理，笔者借此机会与学生探讨了幂为有理数的二项式展开，即牛顿二项式定理.1665年，牛顿将二项式定理推广到有理指数的情形，于是有了方法4.

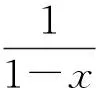
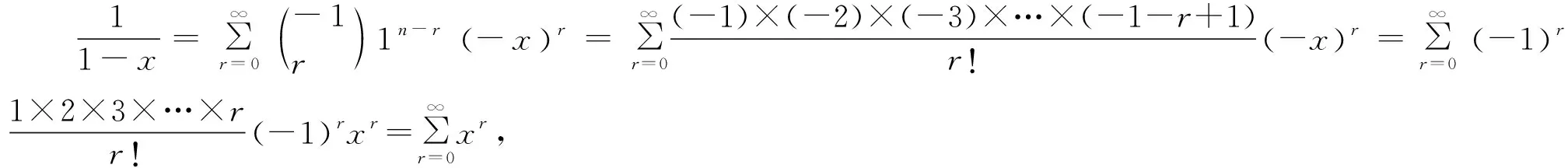
方法4适用于所有幂为有理数的二项式.在和学生共同探讨了四种方法后，学生的积极性大增，想要探索出更多的可能性.笔者引导学生思考麦克劳林级数的实质是用多项式去逼近，因此，目标是找到一个多项式，如果假设这个多项式存在，需要确定的就是多项式的系数，由此想法产生了方法5.

利用等式两侧的同次项系数都要相等，可以得到

a0=1

a1-a0=0

a2-a1=0

⋮

an-an-1=0

⋮

∴a0=a1=a2=…=1，

面对同一道例题的五种不同方法，学生有了更多的选择，逐步消除对麦克劳林级数的畏惧心理.以这五种方法得到的结论为基础，笔者引导学生思考，衍生出更多的麦克劳林级数，于是有了方法6.

方法6(变量代换法):变量代换的思想是一种重要的数学思维方法，可以化繁为简，变未知为已知，大大拓宽了学生的思路，提高了学生学习的积极性.

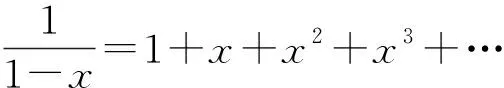
在使用变量代换法的时候，学生容易犯一个错误，下面举例说明.

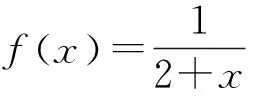
方法6可用于所有已知麦克劳林级数的推广，将已知麦克劳林级数中的变量进行代换，就可以得到新的麦克劳林级数.同时，方法6也适用于复合函数求麦克劳林级数.笔者抓住时机引导学生观察未知与已知之间的区别及联系，通过观察分析得到了方法7和方法8.

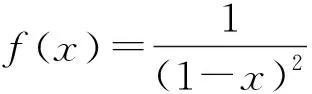
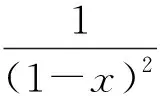
方法7适用于所求函数正好是已知麦克劳林级数的导数.例如，对sinx的麦克劳林级数求导可以得到cosx的麦克劳林级数.

微积分是DP 12数学教学的重点，学生很容易类比逐项求导法联想到是不是也有逐项积分法.

例5求f(x)=ln(1-x)的麦克劳林级数.

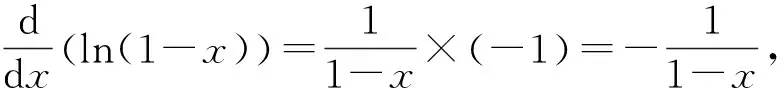
方法8适用于所求函数是已知麦克劳林级数的积分.

在与学生探讨了单个函数的麦克劳林级数后，很自然地过渡到两个及以上函数的加、减、乘、除的麦克劳林级数，从而产生了方法9.

例6求f(x)=exsinx的麦克劳林级数.

方法9(四则运算法)：利用已知级数的加、减、乘、除可以得到新的麦克劳林级数.

方法9适用于已知麦克劳林级数之间的加、减、乘、除.

在DP 11的数学教学中，复数的地位相当重要，复数的概念以及分类等内容能提升学生数学抽象以及逻辑推理的核心素养，利用两个复数相等的条件以及棣莫弗公式可以求某些函数的麦克劳林级数,方法很简捷.笔者引导学生思考如何用复数的方法推导出三角函数的二倍角公式，采用类比的方法迁移到例6中，于是有了方法10.

方法10(复数法)：例6还可以通过复数法解答，利用两个复数相等，实部要和实部相等，虚部要和虚部相等.

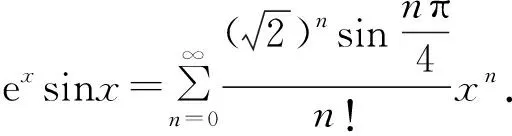
学生常对复数法的绝妙拍案叫绝.DP的复数教学相对于国家课程要求更高，例如对于有限项级数的和acosx+a2cos2x+a3cos3x+…+ancos(nx)，要求学生能构造出acisx+a2cis2x+a3cis3x+…+ancis(nx)，逆向运用棣莫弗公式将其转化为acisx+(acisx)2+(acisx)3+…+(acisx)n,然后利用等比数列的求和公式和复数的共轭将其化简，最后利用实部与实部相等得到有限项级数的和.整个过程需要学生在已有的基础知识上，有意识地建立起新旧知识间的联系，通过演绎推理得到新旧知识间的逻辑关系.

方法10非常巧妙，可以一举两得，让学生体会到数学的和谐简单之美.复数与三角函数以及向量的联系十分紧密，复数法主要适用于求解三角函数的麦克劳林级数，也适用于求解三角函数与指数函数共同构成函数的麦克劳林级数.

积分的章节介绍了对有理函数进行裂项后再积分，笔者引导学生思考有理函数的麦克劳林级数是否也可以采用裂项法，下面介绍方法11.

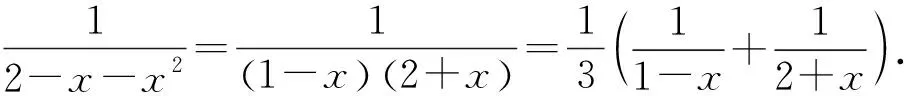
方法11适用于所有可裂项的有理函数.裂项后通常还要用到变量代换法，即方法11通常要和方法6联合起来使用.

在对数函数的求导教学中，总结出的准则是先利用性质化简，然后结合导数的四则运算法则和复合函数求导法则进行求导.笔者引导学生思考对数函数的麦克劳林级数是否也遵循先化简的原则，由此想法引出方法12.

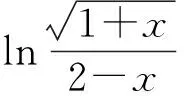
然后利用变量代换法就可以求出麦克劳林级数，这里不再展开.

由此可见，根据函数的特点以及性质进行变形，选择恰当的形式，灵活选取公式可以大大简化计算过程.方法12主要适用于求解对数函数的麦克劳林级数，以及求解三角函数中能利用三角恒等式转化为已知麦克劳林级数的类型.

在介绍分部积分时，有一类函数(例如exsinx)在多次分部积分后具有规律性，积分之后产生的一部分和原式一样，笔者引导学生思考求导之后的函数是否也有循环，于是产生了方法13.

例9求f(x)=esinx的麦克劳林级数.

方法13(链式法则):利用链式法则对f(x)=esinx两边关于x求导可以得到f′(x)=esinx·cosx=f(x)·cosx.对上式两边关于x求导可以得到f″(x)=f′(x)·cosx+f(x)(-sinx)=f′(x)·cosx-f(x)·sinx，对上式两边关于x求导可以得到f‴(x)=f″(x)·cosx-f′(x)·sinx-[f′(x)·sinx+f(x)·cosx]，化简得f‴(x)=f″(x)·cosx-2f′(x)·sinx-f(x)·cosx.对上式两边关于x求导可以得到f(4)(x)=f‴(x)·cosx-f″(x)·sinx-2[f″(x)·sinx+f′(x)·cosx]-[f′(x)·cosx-f(x)·sinx].

化简得f(4)(x)=f‴(x)·cosx-3f″(x)·sinx-3f′(x)·cosx+f(x)·sinx,

…

如此一直下去，可以得到

f(0)=1，f′(0)=1，f″(0)=1，f‴(0)=0，f(4)(0)=-3，…

方法13适用于求导后具有规律性的函数，求导之后产生的一部分和原式一样，这样可以用原式替代这一部分，然后在替代后的微分方程两边求导，如此一直下去，最后结合定义法就能得到麦克劳林级数.

三、 结语

为了让学生能更加深刻地理解麦克劳林级数，消除畏惧心理，切实体会到麦克劳林级数的美，笔者在麦克劳林级数的教学中以数学概念的抽象过程为载体，借助数形结合让学生亲身经历研究一个数学对象的基本过程，使学生在探究问题的过程中从有限中认识无限，从近似中认识精确，从量变中认识质变，亲身体验数学概念形成的过程.同时，总结出的13种方法之间充满关联，前后呼应.整个过程中，学生在教师的指导下积极思维，贯通思路，加强理解，最终达到运用自如的目的.