比对试题悟真知 追寻结构“道”归来
510800 广州市花都区第二中学 杨伟达
511316 广州市增城区荔城中学 林树宏
在解题教学中,如何提高学生的解题效率?相关问题一直困扰着数学教育工作者.笔者举例进行探究.
一、 试题呈现
例1(2019届广州市高三调研测试理-17) 在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2B-cos2C=sin2A+sinAsinB.
(1)求角C的大小.
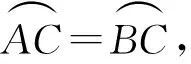
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB.
(2)求证:BC2-CE2=CE·DE.
(3)已知OA=4,E是半径的中点,求线段DE的长.
二、 比对求同,架接联系,构建知识网络
比对上述两道题,例1是一道高中数学试题,主要考查了有关解三角形的综合内容;例2是一道初中数学试题,主要考查了有关圆的综合知识,观察两题,笔者发现了一个关联结构,例1为□2-△2=○2+△○,例2为□2-△2=△○.观察、比对结构式,发现等式左右两边形式相似,分析思路类似,只是选取的角度不同(一道题作为已知条件,以角的形式出现;而另一道题作为证明结论,以线段的形式出现).需要对试题的这种结构进一步逐层分析,直到满足已知条件为止,这样问题即可完美解决.
三、 比对求异,拓宽视野,寻找最优解法
(一)对于例1
对于例1已知部分的□2-△2=○2-△○这一结构,即cos2B-cos2C=sin2A+sinAsinB.
分析1:移项后得□2=△2+○2-△○,比对这一结构,发现与一个公式类似,不妨先将角变为边,再用余弦定理解答即可.这也体现出命题专家考查学生的初衷.
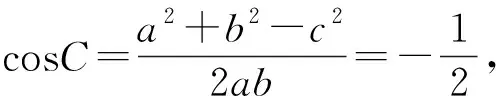
分析2:左边是□2-△2,化简为(□+△)(□-△),观察发现,许多学生将其变成□+△或□-△时不能再继续化简,而个别学生发现消元后化简(消去∠A)即可,但涉及积化和差、和差化积、倍角公式及三角形内角和公式等,化简运算比较繁杂,需要较高的运算技巧.

分析3:先用降幂公式,把2次式降为1次式,即为■1-▲1=●1+▲●,再用和差化积、三角形内角和公式,消元后(消去∠A)化简,对技巧要求较高,不少学生对此感到胆怯,不能再继续化简.

(二)对于例2
对于例2求证部分的□2-△2=△○这一结构,即BC2-CE2=CE·DE.
思考1直接用平方差公式化简为(□+△)·(□-△),观察图1,发现找不到合适的线段替换□+△或□-△,所以这种情况不可能.
思考2将△○换成☆2,变成勾股定理□2-△2=☆2,在三角形中找直角,观察发现,图1中找不到直角,所以这种情况也不可能.
思考3移项后变成□2=△2+△○,最后得□2=△(△+○).观察图1,可以找到一条线段☆替代△+○,即变为□2=△☆,变形后线段成比例,即可转化为由两个三角形相似,问题得到解决.
例2(1)(3)解答略.
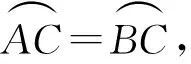
四、 比对释悟,追寻“道”法
比对上述两道试题,笔者得到如下教学感悟.
(一)加强对公式结构的再认识
一直以来,数学问题公式化是数学知识的考查重点,也是命题专家希望看到的初心.它要求学生熟练掌握,灵活应用,强调数学方法和技巧,令不少学生有畏惧心理.尽管当前教学改革的方向已经发生改变,考试命题的专注点也已经改变,但可以肯定的一点是,数学始终离不开公式.因此,加强对公式结构的再认识是学生学好数学的重要法宝.一个数学问题可以从不同的角度审视,往往需要用到不同的数学公式.因此,首先要做好公式的选取;其次审视公式的结构,做好公式的正用、逆用;最后对一些公式进行变形及转化(这里需要学生有更高的解题技巧).例如人教版高中教材必修4的三角公式,必修5的正、余弦定理等公式都是高考的命题热点,公式多而繁杂,学生要记得准、记得快、记得牢,就必须厘清公式的来龙去脉,关注公式结构,多做公式推导.当前,不少高中学生运用公式时丢三落四、虎头蛇尾,要确保原式不变、答案准确,常常需要培养“缺什么补什么”“缺什么找什么”“缺什么改什么”“涂什么改什么”“问什么设什么”“乘什么除什么”“加什么减什么”等常见的思维习惯.
(二)加强对问题审题的训练
审题是解题教学的必备环节,是提升学生数学素养、养成严谨思维的最好载体.选取一道好题,选好一个角度,做好例题的导向功能,能极大提高学生的数学兴趣.对于典型的数学例题,可以从不同的角度思考、分析,逐层推进,层层分解,最终找到解决问题的方法.这些需要教师在平时的教学中重点剖析,这样学生才能养成良好的审题习惯.诚然,不少学生能够熟练记住公式,可一到考试就无从下手,不知道选用哪一个公式,有时公式虽然写了,但常常错误百出,搭不上题,缺少目标和条件,缺少具体联系,缺少审题环节和理解题意.更有甚者,一些学生还没有看清楚已知条件和结论就匆匆下笔做题,缺少分析思路,长此以往会形成一个恶性循环.俗话说“好题读三遍”,教师一定要让学生理解题目的意思后再下笔做题.
五、 比根寻源,链接高考
比对教材,笔者发现人教版普通高中课程标准实验教科书必修5第20页的第14题有相似的关联结构;比对高考,2019年全国Ⅰ卷第17题中也可以找到类似的影子.
教材原题(人教版必修5 P20-14) 在△ABC中,求证:c(acosB-bcosA)=a2-b2.
点评:本题考查了三角形的综合问题,主要涉及正弦、余弦定理等.对于□2-△2结构,有几种思路进行发散.
高考题(2019全国Ⅰ卷理-17) △ABC的内角A,B,C的对边分别为a,b,c.设(sinB-sinC)2=sin2A-sinBsinC.

点评:对于(□-△)2=○2-□△这一结构,先用完全平方公式,化简后变为□2+△2=○2+□△,再用余弦定理解决.
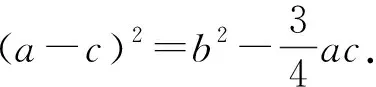
(1)求cosB的值;
点评:对于(□-△)2=○2-□△这种结构,比对2019年全国Ⅰ卷理科数学第17题,发现它们的结构有异曲同工之妙.

