利用“构图法”解决一类含根式的最值问题

225002 扬州大学附属中学 张 顺

面对含根式的最值范围问题，学生经常觉得题目很“美”，但在考场上无从入手，这是学生的薄弱环节.笔者从四种构图方式切入，探究“构图法”的解题应用.

一、 利用两点距离公式构图

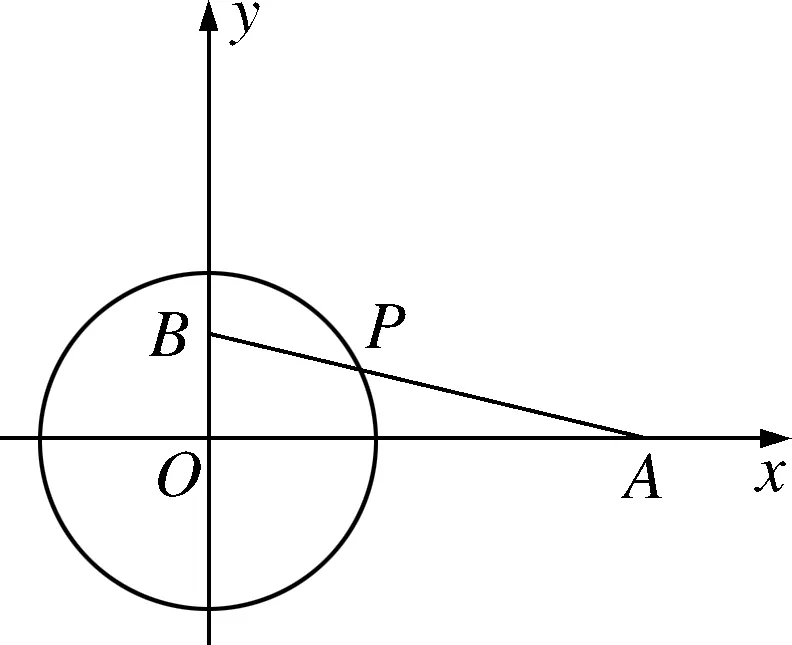
图1

二、 利用面积公式构图

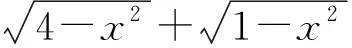
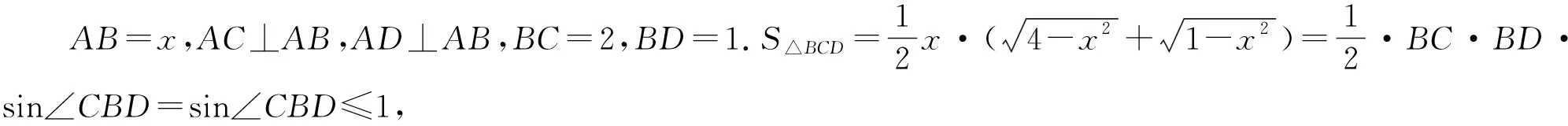
图2

三、利用余弦定理构图

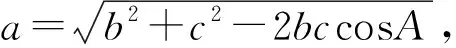
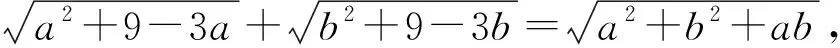
图3

四、 利用勾股定理构图

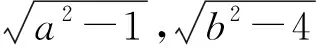
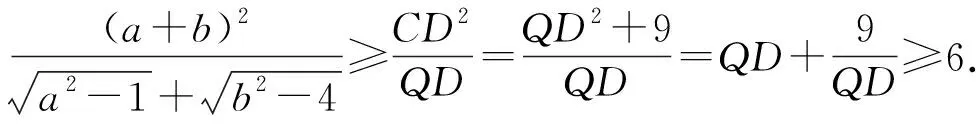
图4

通过观察代数式的结构特征，合理构造图形，从而找到几何意义，将复杂的根式问题化简，进而解决这类问题.解题过程既体现了转化化归的思想，也体现了数形结合的思想，体现出数学之美，这种解题方法具有一定的创造性，需要学生平时多观察，多积累，锤炼“火眼金睛”.