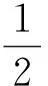线上教学背景下的师生有效互动实践探究
——以“平分三角形面积问题”的专题课为例
200126 上海市民办福山正达外国语学校 支 鑫
教学互动是指学生与教师、学生与学生之间在教学内容、教学情境等方面的互动.有效互动的形式主要包括师生互动、生生互动以及学生与文本互动.线上教学过程中,师生课上交流的距离变远了,但课后交流的距离却变近了.此消彼长,这为数学专题课教学拓展了时间和空间.
良好的互动是围绕教学目标展开,通过问题设计、比较分析、表达与交流等途径,引导学生进行深入思考,产生思维碰撞的火花,从而实现教师与学生的共同发展.专题探究课不仅仅是对教材内容的拓展应用,同时更注重培养学生发现和提出问题的能力,以及进行综合性、探究性学习的能力.因其内容坡度大、思考内容多、思考过程中个体差异大,故传统课堂教学很难让每位学生充分体验到探究的完整过程.为此,笔者充分利用线上教学的优势,采取多种互动方式,充分调动学生自主探究的积极性,同时结合变式教学,对题目的条件进行变式和推广,引导学生由浅入深,步步深化,从而提高教学效率.
一、 研读讲义,独立思考
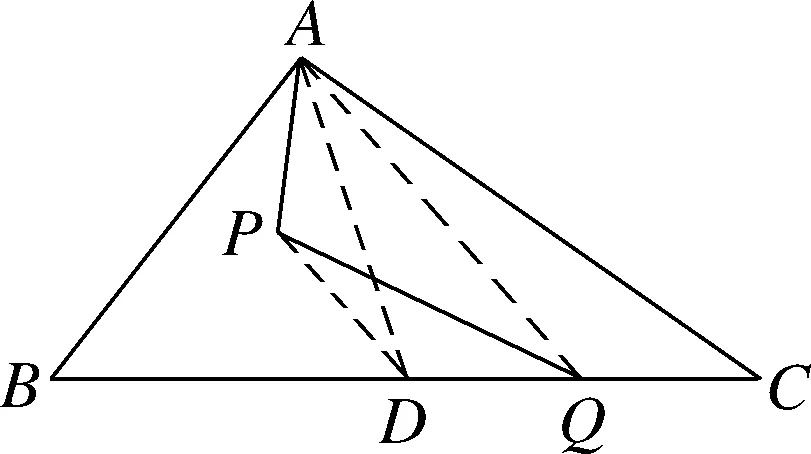
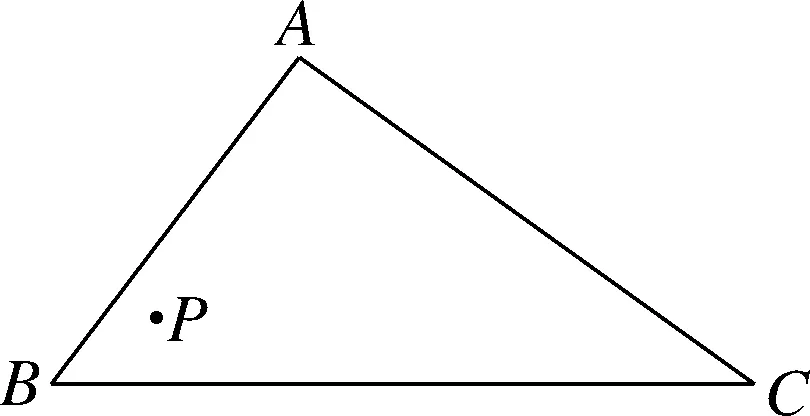
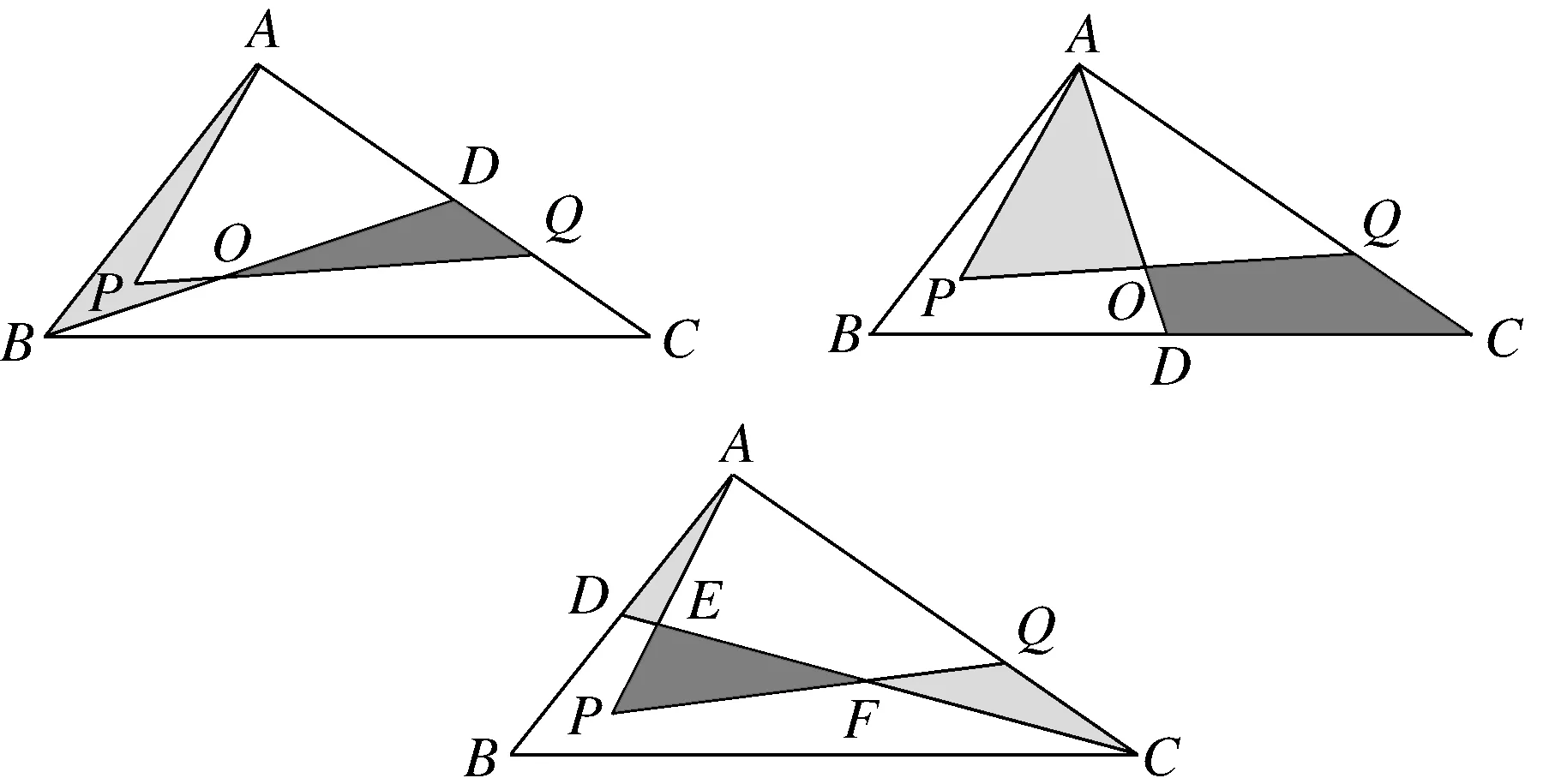
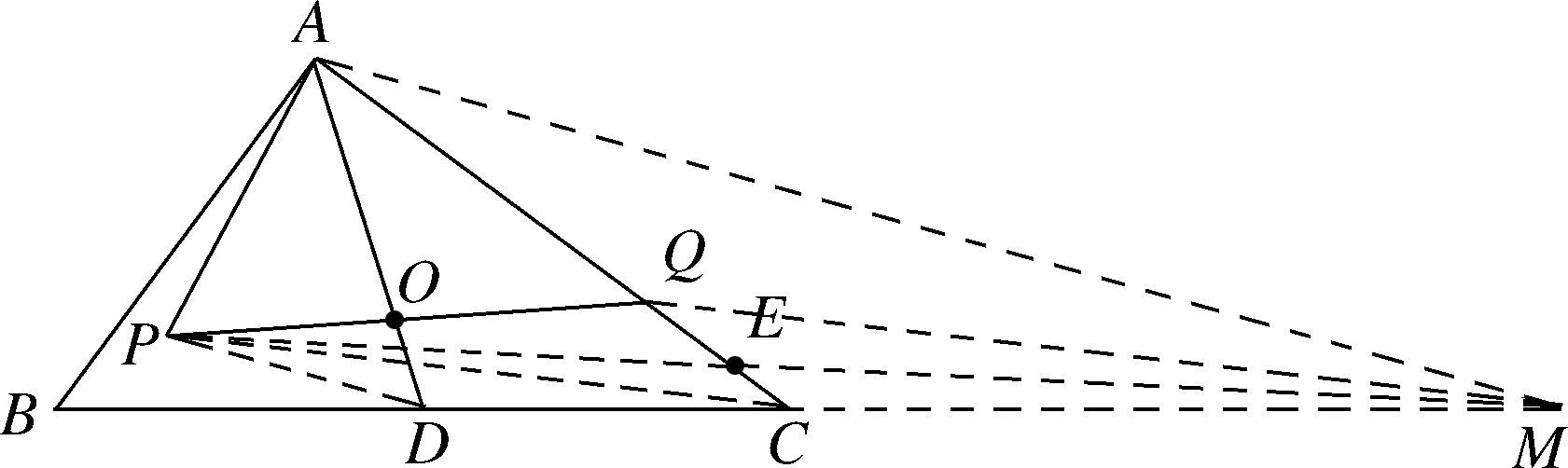
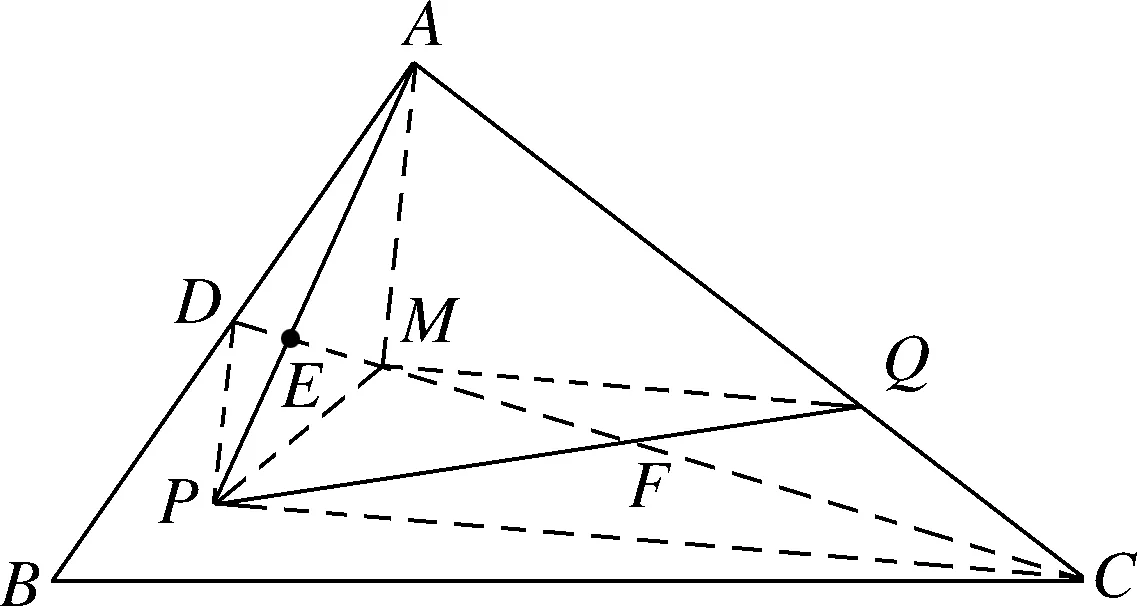
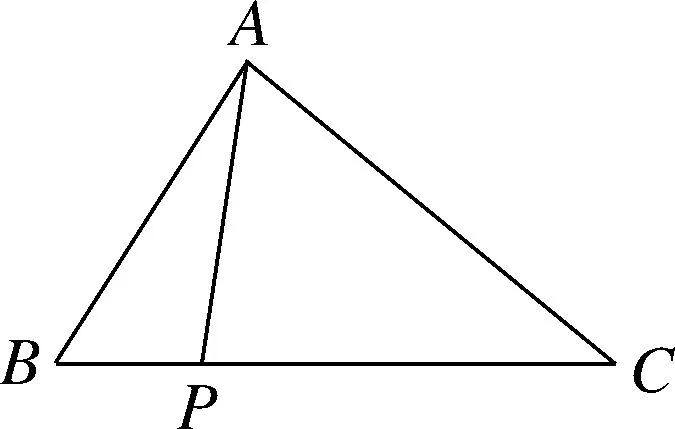
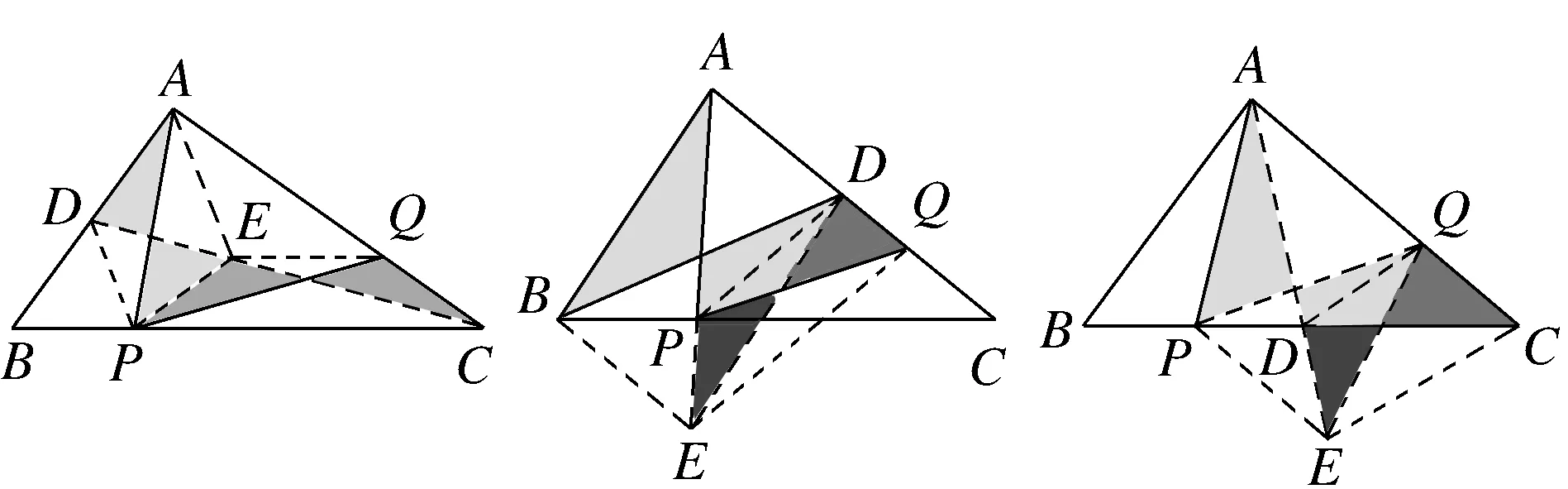
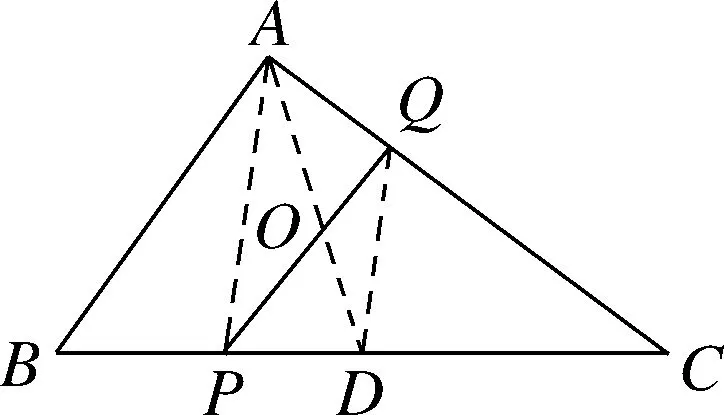
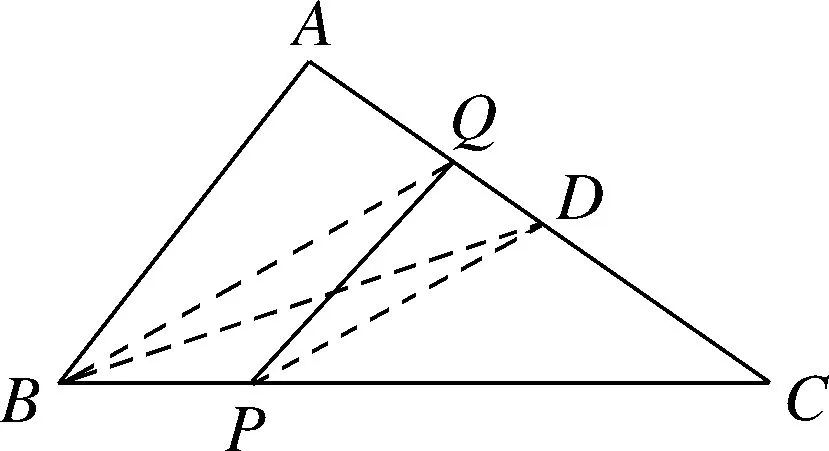
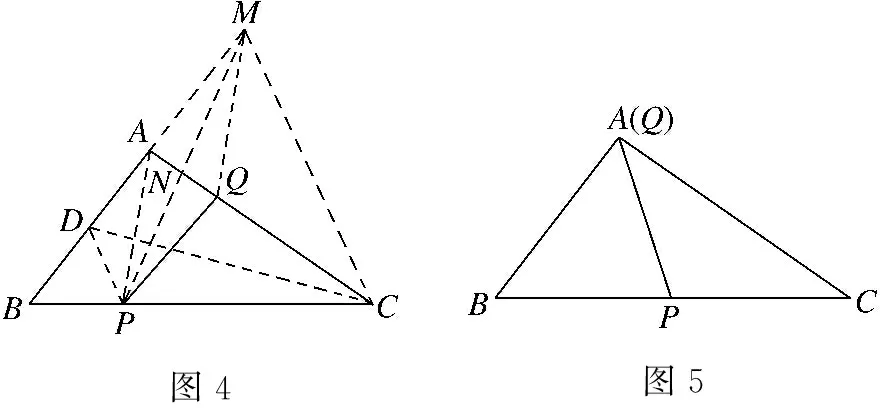
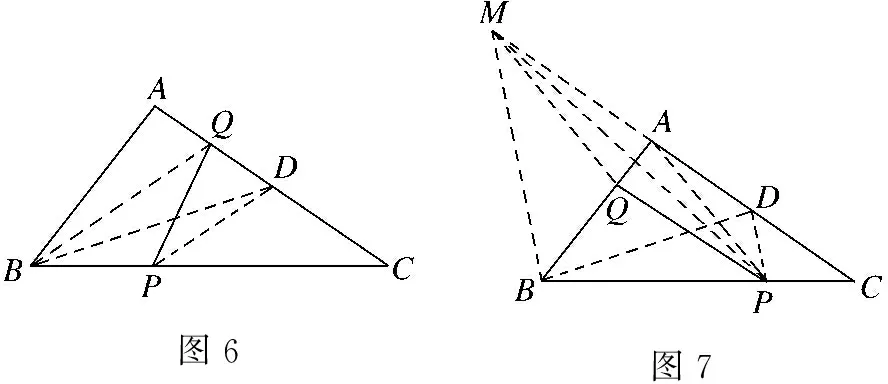
问题1如图1,点P为△ABC边BC上一点,且BP 图1 从学生的作业完成情况来看,大部分学生都能想到作三角形的一条中线,但实际上学生对这条中线所起到的作用并不明确,对于后续如何确定点Q的位置也没有思路.根据学生作业情况的反馈,教师提供了一份阅读讲义(如表1所示),阐述分析思路,引导学生通过研读讲义,自行找出问题中的条件与涉及的知识点之间的内在联系,从而独立解决问题. 表1 “过三角形边上一点作直线平分三角形面积问题”阅读讲义 “书读百遍,其义自见”,反复阅读讲义的过程也是学生进行深入思考的过程.学生受讲义启发,尝试再作三角形中线.不难判断点一定在边上.那么只需利用平行线的性质推论,构造两个面积相等的三角形,进而可以找到点Q的位置. 画法1:取BC边的中点D,联结AP,AD(如图2所示).过点D作AP的平行线,与AC交于点Q,则直线PQ即为所求. 图2 从上述解题过程可以看出,解决此题的关键在于画出中线,找到需要进行面积互换的两个三角形,并由此画出平行线,进而找到平行线与三角形一边的交点,即为点Q.此例的设计充分运用了平行线的性质推论,为后续问题的解决提供了最基本的范例. 与此同时,还有学生提出疑问,既然可以通过作BC边上的中线来解决问题,那么若作另两边的中线,方法是否相同?于是开始尝试第二种方法,作AC边上的中线. 画法2:取AC的中点D,联结PD,BD(如图3所示).过点B作PD的平行线,与AC交于点Q,则直线PQ是△ABC的面积平分线. 图3 总之,高校作为人才培养的重要阵地,必须紧跟时代发展的步伐,迎接大数据时代发展带来的机遇和挑战。加快高校学生管理信息化建设的步伐,才能在充分发挥大数据价值的基础上,促进高校学生管理信息化数据分析能力的不断提升,为培养符合社会发展需求的综合型应用人才奠定坚实的基础。 画法2的产生是由于个别学生提出猜想,主动尝试并成功解决,得出结论,于是教师建议学生自行录制讲解视频,将自己的思考过程和题目的做法完整呈现,与其他学生交流分享.学生在录制讲解视频的过程中反复修改讲解稿,学习数学语言的使用规范,研究作图方法和视频录制方法,锻炼了动手能力以及使用数学语言表述问题的能力.与此同时,其他学生通过观看视频、小组交流也掌握了此题的作图方法.订正作业的完成情况也得到了改善.由文本互动到生生互动,教师对学生提交的线上作业及时给予反馈,不断增强学生的自信和继续探究的兴趣. 完成前两种画法后,师生共同提出第三种画法,作第三条边AB边上的中线,结果又会如何呢?为了更好地处理这个问题,首先需要总结前两种方法中的规律.师生发现本题的解题思路分为两步.第一步,画出三角形的一条中线,构造一个三角形使其面积等于原三角形面积的一半;第二步,利用平行线的性质,构造等积三角形. 本节专题课进行到此,前两种方法的解答皆由学生通过自行阅读讲义或观看讲题小视频来完成.但在画法3的尝试中,学生还是遇到了困难.此时教师登场,对此种方法进行讲解.通过构造同底等积的三角形,将不规则图形的面积巧妙转化为规则图形的面积. 学生在画图的过程中发现了问题,在过点C作PD的平行线时,发现它与△ABC的边的交点并不在三角形内部(如图4所示).即用于交换的面积相等的两个三角形△BMP、△BCD有部分(△AMN)不在△ABC中,需再次利用平行线的性质,在△ABC的内部构造△PNQ,使得S△PNQ=S△AMN. 画法3:如图4,取AB的中点D,联结CD,PD.过△ABC的顶点C作PD的平行线,与边BA的延长线交于点M.联结AP,过点M作AP∥MQ,与AC交于点Q.则直线PQ是△ABC的面积平分线. 从提出质疑到问题解决,学生经历了“研读讲义,独立思考”“生生互动,小组交流”“师生联手,教学相长”三种互动方式.在线上教学背景下,师生形成了一个互相信任的“学习共同体”,加强了学生对数学知识和思想方法的理解和变通,培养了学生自主分析和解决问题的能力.在这一过程中,教师扮演的角色与其说是说教者,不如说是交流互动平台的提供者. 学生通过画图、研究发现画法之所以不同的原因之一是受点P的位置影响,从而教师提出思考.若点P为动点,那么点P的位置与以上三种方法之间是否有关联,有什么关联?教师将问题一般化,但解决问题的方法实质并没有变.师生再接再厉,开始迎接第二个挑战. 问题2点P为△ABC边BC上任意一点,请过点P作直线l,使该直线把△ABC分成面积相等的两个部分(尝试用多种方法画图). 图4图5 图6图7 基于以上思考,教师继续追问:若点P不选在三角形的边上,而是选择在三角形内部,会发现方法失效.对条件进行微调,在变直为曲的情况下,探索画法是否仍然守恒. 问题3△ABC内有一点P,试在BC上确定点Q,使得折线A-P-Q恰好将△ABC的面积平分. 作法:如图8,取BC的中点D,联结PD,过A作PD的平行线交BC于点Q,则折线A-P-Q即为所求. 图8 本题将点P的位置从“三角形上”移动到“三角形内”,题目的条件虽然发生改变,但解决问题的方法依然离不开画中线和平行线再构造等积三角形.这是对上述画法的推广应用,学生可以拾阶而上,类比迁移,逐步感悟数学思想. 学生在经历了问题2的三种方法后,在知识层面上对于平行线性质推论的掌握和应用能力有了较明显的提升.同时在分析问题、解决问题等思维能力方面,学生也会主动将问题与学习过的知识建立联系,大胆尝试,小心求证,寻求解决问题的方法.更令笔者欣喜的是,学生还会不断提出新的问题,自主寻求新方法,为这类问题的解决方案提供了更多的可能性. 问题3的作业完成情况有了很大进步.此时,已有学生提出,似乎当点P位置变化时,方法也会不同.于是教师再次乘胜追击,布置问题4.将原图中点P的位置稍作调整,探寻点P的位置对画法的影响. 问题4如图9,△ABC内有一点P,试在AC上确定点Q,使得折线A-P-Q恰好将△ABC的面积平分. 图9 学生的分析思路非常有意义,最可取之处在于有判断、有构思.(1)判断点Q在边AC上;(2)假设了三种不同中线的画法(如图10所示),明确了要交换部分的面积(浅灰部分与深灰部分互换),为进一步画图提供了直观的思路;(3)选择熟悉的、较规则的图形进行面积互换. 图10 下面展示学生的两种画法. 画法1:如图11,取BC的中点D,联结PD,过A作PD的平行线,与BC的延长线交于点M,PM与AC交于点E,联结PC,过点M,作MQ∥PC,交AC于点Q.AD与PQ交于点O. 图11 画法2:如图12,取AB的中点D,联结CD,过A作PD的平行线交CD于点M;过点M作MQ∥PC,交AC于点Q.通过平行线构造两组面积相等的三角形,实现面积互换. 图12 学生自行提出问题、探究解决方案,研究兴趣高涨.于是笔者顺势再次调整题目的条件,将点P位置重新移回到三角形边上. 问题5如图13,点P在△ABC的边BC上,试在AC上确定点Q,使得折线A-P-Q恰好将△ABC的面积平分. 图13 在解决问题的过程中分别选择了三种中线的情况,但用到的知识和方法大体相同,则画法1共有三种情况(如图14所示). 图14 问题1到问题5的教学共持续一周时间.线上教学实施过程中,学生的课程学习主要依靠空中课堂和线上直播的方式来完成.在居家学习期间,学生每日的学习时间较为自由,可根据需要自行安排.同时,利用钉钉平台的视频会议模式,也可有效开展小组协作、师生互动等活动.在疫情防控、居家隔离的大环境下,学生面临着学习方式的改变,势必存在自主管理靠自己、课堂效果难监测等问题.但与此同时,教师可充分发挥线上教学在时间和空间上的优势,为学生提供各类学习资源,强调以学生为主体的学习模式,从而激发学生学习的积极性和创造性.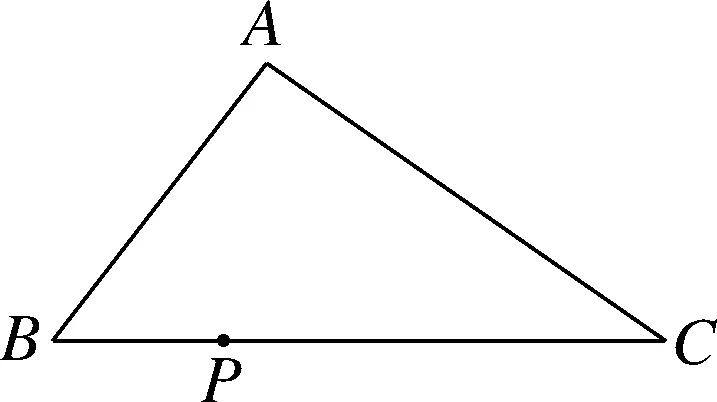

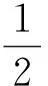
二、 生生互动,小组交流
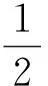
三、 师生联手,教学相长
四、 类比迁移,逐步感悟数学思想