正断层错动圆形隧道结构影响因素及损伤分析研究

陶连金,张乃嘉,安 韶

(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)

引言

我国处于欧亚地震带与环太平洋带之间，纵横交错多条活动断裂带。近年来，随着川藏铁路的修建及城市地铁兴起，长距离交通、输水、城市综合管廊等生命线系统在国内正在进行大规模建设。由于隧道路线往往取决于其功能需求，避让原则常常无法实现。例如，北京地铁12号线穿越南口—孙河断裂、黄庄—高丽营断裂；乌鲁木齐地铁1号线穿越九家湾断层组[1]；香炉山引水隧道穿越龙蟠—乔后、丽江—剑川及鹤庆—洱源等全新世活动断裂[2]。汶川地震震害经验表明：穿越活动断裂带隧道在地震动与断层错动作用下破坏非常严重，且断层错动是引起结构破坏的主要因素[3-4]。因此，研究断层错动作用下隧道结构的影响因素及破坏机理对隧道结构设计具有重要意义。

目前，穿越活动断裂带隧道结构研究方法主要包括模型试验法及数值模拟法。ZHAO等[5]提出采用纤维素性混凝土作为跨断层节段式隧道柔性接头的材料，并通过模型试验和数值模拟验证了纤维素性混凝土的适用性；刘学增等[6]以棋盘山隧道为背景，开展1∶50相似模型试验，并指出逆断层错动在断层迹线附近地层形成剪切带，隧道最终破坏形式主要为剪切破坏；王道远等[7]开展了1∶30抗错断模型试验，对逆断层黏滑错动下隧道衬砌结构应变、受力进行对比分析，结果表明，断层黏滑错动具有显著区域性特征，活动盘侧最大接触压力错动前后变化显著；闫茜等[8]考虑了活断层蠕滑与震动对高铁路基变形的影响，认为逆断层的影响范围显著大于正断层，且已有蠕滑累积量是震动发生后路基变形的重要影响因素。在数值模拟方面，焦鹏飞[9]采用有限差分法分析了逆断层错动对隧道结构的影响，试验结果表明错动对主盘内隧道影响较大；梁建文等[10]对比分析了45°倾角正、逆断层错动作用下盾构隧道的破坏特点，并指出正断层错动下，环间螺栓易发生受拉破坏，逆断层错动下，混凝土管片易发生破坏；ZHONG等[11]通过数值模拟对断层位移、隧道与断层交角、围岩力学性质等进行参数分析，并通过损伤指标评估了隧道在走滑断层作用后的破坏程度。

以上研究成果对于穿越活动断裂带的地下结构工程具有一定指导意义，但存在以下不足。(1)已有研究对断层位移、隧道埋深、破碎带宽度等进行了影响因素分析，讨论了随着影响因素的改变，结构响应或破坏的变化趋势，但却忽略了对结构响应增加模式的分析，即通过结构响应增加率的变化确定结构响应是线性增长(结构响应增长率不变)、指数增长(增加率逐渐增加)或对数增长(增加率逐渐降低)。(2)在断层错动作用分析中，通过物理试验及数值模拟可定性地表达隧道结构变形及拉压剪切破坏，但缺少相关定量指标为工程设计提供参考。

为进一步对断层错动作用下隧道结构响应及破坏特征进行研究，采用有限元方法。首先，对断层位移、土-隧道摩擦系数、隧道埋深进行影响因素分析；其次，采用混凝土损伤模型定量表征隧道的变形和破坏。以上研究期望对相关穿越活动断裂带工程提供依据和参考。

1 正断层错动土-隧道有限元数值模型验证

正断层错动诱发隧道变形破坏的离心机试验装置见图1，断层倾角为70°，试验通过液压加载装置实现断层的错动。基于离心机试验，彭佳明[12]分析了隧道的纵向应变分布规律，对沿纵向土层位移变形模式进行了拟合，之后通过有限差分软件FLAC3D建立三维土-隧道模型，分析不同纵向长度及边界条件下的影响规律。

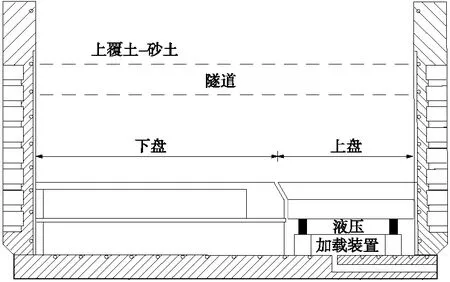
图1 离心机试验装置示意

ANASTASOPOULOS等[13]通过模型试验验证了断层错动分析中采用有限元软件ABAQUS时，数值模拟结果与模型试验结果吻合较好。因此，本文选择该软件进行数值模拟分析。其中，土层及衬砌结构参数均与文献[12]一致，见表1。隧道结构刚度考虑了折减，折减系数取为0.65；衬砌外径为5 m，厚度为0.36 m，隧道埋深为7.5 m；土与隧道之间摩擦角φ为20°，摩擦系数取为0.24tan(2φ/3)[14]。

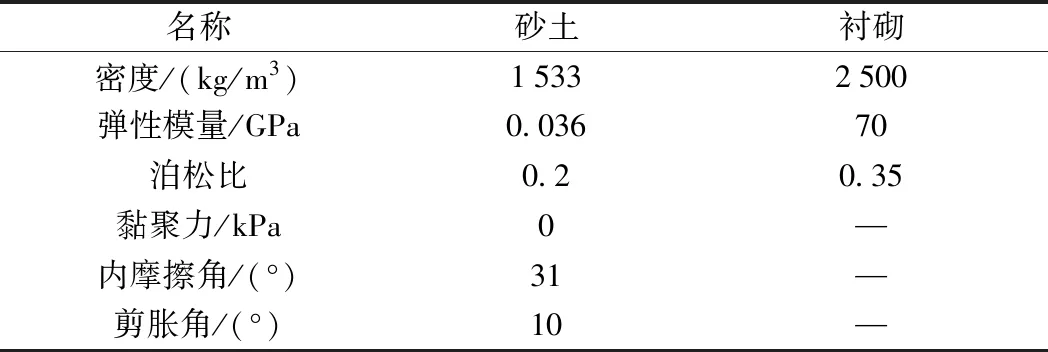
表1 土-隧道模型力学参数

建立三维土-隧道有限元模型，模型尺寸与原型一致，其尺寸为57.5 m(长)×17.5 m(宽)×25 m(高)，上下盘纵向长度为1∶2，纵向共划分60份网格，圆形隧道沿环向共划分72份网格，模型单元总数为118 800。土体介质与隧道结构均采用八节点减缩积分实体单元C3D8R模拟，土体本构模型服从Mohr-Coulomb破坏准则。模拟分析分为两步：①初始地应力平衡；②施加断层位移[15]。网格划分及不同步骤模型边界条件见图2。

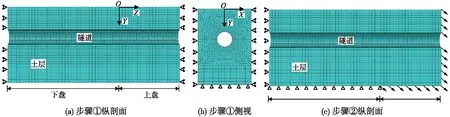
图2 模型网格划分及边界条件

施加正断层竖向位移0.8 m，相应的水平向位移为0.29 m。距隧道轴心8.8 m处土层沿纵向的竖向位移分布见图3，隧道纵向应变云图及拱顶纵向应变与试验数据对比见图4。由图3可知，数据模拟土层竖向位移沿纵向分布曲线与试验结果及拟合公式[16]一致。由图4可知，数值模拟与试验数据的隧道拱顶纵向应变最大值分别为1 508 με，1 697 με；拱顶纵向应变分布趋势与试验结果一致。由以上分析可知，采用的有限元数值模型是合理的。

图3 距隧道轴心8.8 m土层位移曲线

图4 隧道拱顶纵向应变曲线

如图4所示，当隧道纵向长度取57.5 m时，仅能表现出下盘隧道拱顶纵向受拉的影响。刘学增等[17]指出正断层错动作用下，上盘内隧道拱顶纵向受压，下盘内隧道拱顶纵向受拉，因此，有必要确定数值模拟中合理的纵向长度。

MA等[18]指出当侧向边界不小于结构跨度的6～10倍时，边界效应对结构的影响可忽略不计，因此，模型侧向边界距离增加至30 m，即结构跨度的6倍。其次，分别增加数值模拟中纵向长度至90，120 m，上下盘纵向长度均为1∶1，隧道纵向应变云图见图5。由图5可知，随着纵向长度增加，上盘隧道拱顶纵向受压逐渐表现出来。隧道拱顶纵向应变及竖向位移见图6。

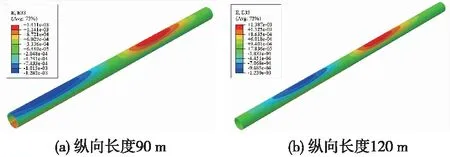
图5 不同工况纵向应变云图(单位：ε)

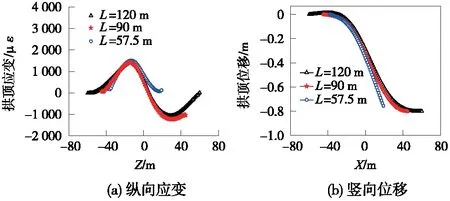
图6 隧道拱顶纵向应变及竖向位移曲线

由图6可知，当隧道纵向长度为90 m时，隧道纵向应变及竖向位移均未达到稳定，当隧道纵向长度取为120 m时，隧道纵向应变两侧边界处接近于0，竖向位移达到平缓阶段，较为全面地反映了结构纵向受力状态。除此以外，随着隧道纵向长度增加，隧道结构拉应变最大值分别为1 508，1 411，1 387 με；隧道结构压应变最大值分别为1 449，1 282，1 230 με。即隧道结构拉压应变最大值随数值模型纵向长度增加逐渐降低，边界条件对隧道结构响应的影响逐渐减小。因此，在后续模拟中数值模拟纵向长度均取120 m，最终采用有限元数值模型尺寸为120 m(长)×30 m(宽)×25 m(高)。

2 结构响应影响因素分析

断层错动作用下，隧道结构受拉压剪弯作用发生破坏。因此，为全面反映隧道响应，选择结构纵向拉压应变、环向剪应变及沿纵向的截面弯矩进行分析。对断层位移、土-隧道摩擦系数及隧道埋深3种影响因素进行参数分析，重点研究结构响应增长率的变化趋势。数值模拟共分为7种工况，见表2。

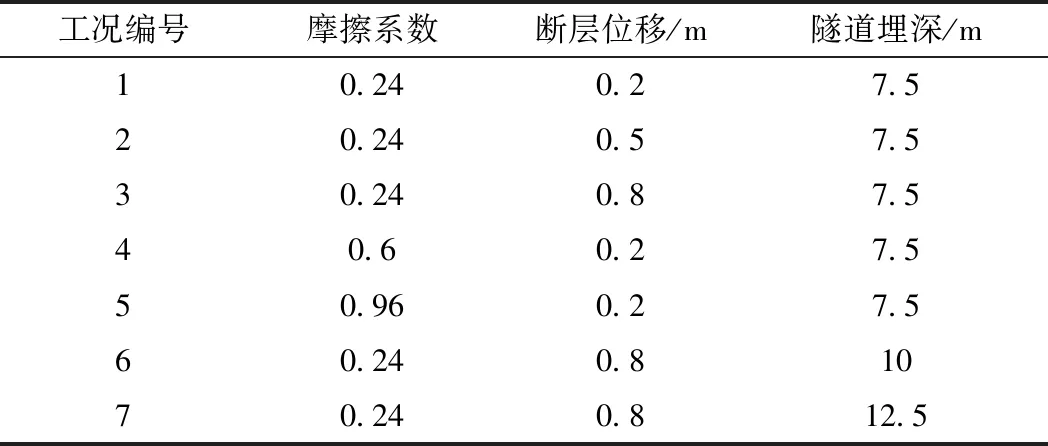
表2 数值模拟工况

2.1 断层位移

其他参数不变时，分别施加正断层竖向位移0.2，0.5，0.8 m，对应的水平向位移为0.073，0.18，0.29 m(工况1、2、3)，隧道纵向拉压应变极值见图7。与工况1对比，工况2、3拉应变最大值分别增加了118.1%、205.5%；工况2、3压应变最大值分别增加136.8%、242.6%。隧道剪应变见图8，由图8可知，隧道剪应变沿隧道轴向对称分布，与工况1对比，工况2、3剪应变最大值分别增加了86.1%、133.1%。以工况1为例，沿隧道轴向截面弯矩分布曲线见图9，弯矩沿错动位置处向两侧延伸呈反对称分布。不同工况弯矩极值对比见图10，其中，正弯矩最大值出现在下盘-17 m处，负弯矩最大值出现在上盘16 m处。与工况1对比，工况2与3正弯矩分别增加了122.2%、220%；负弯矩分别增加了112.7%、187.9%。由以上分析可知，随着断层位移增加，隧道响应逐渐增加。

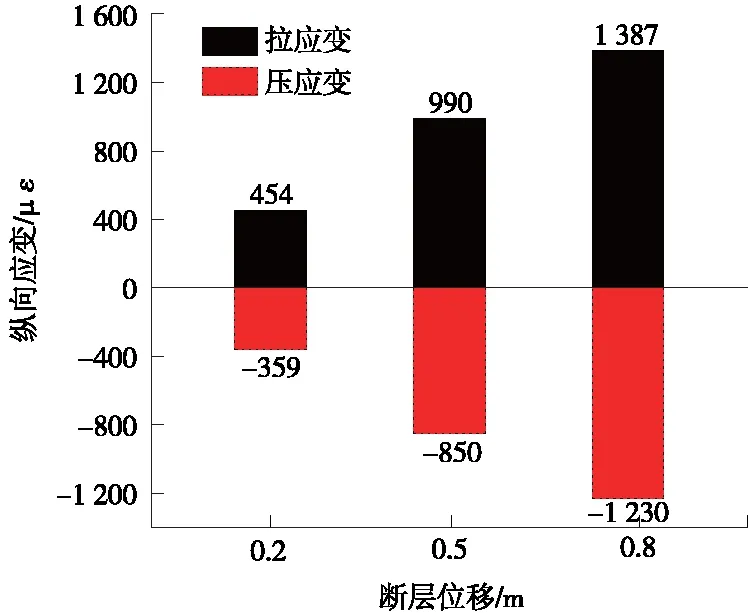
图7 不同断层位移纵向应变极值

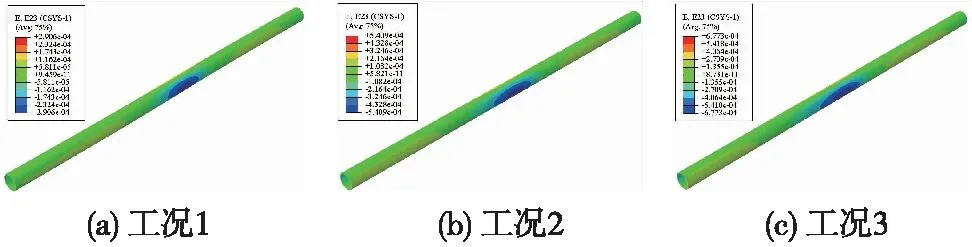
图8 不同断层位移剪应变云图(单位：ε)

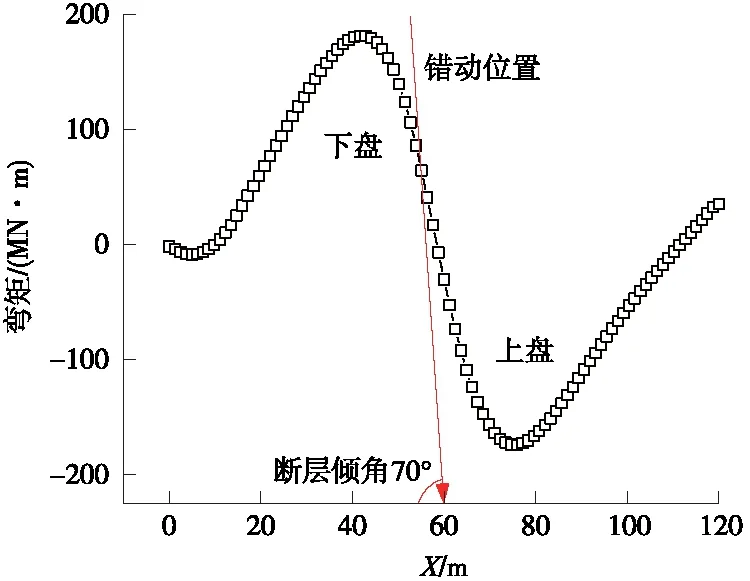
图9 工况1纵向弯矩分布曲线

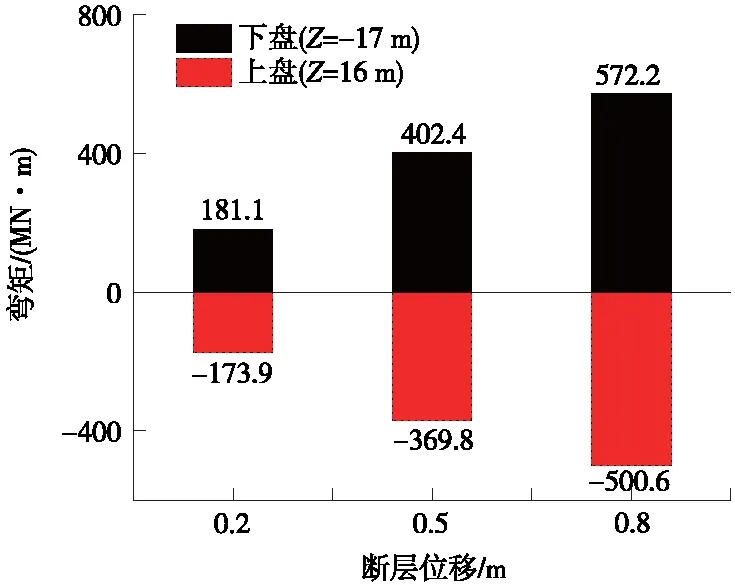
图10 不同断层位移弯矩极值

各指标结构响应增长率变化趋势见图11。由图11可知，结构响应增长基本为线性增长，但增长率变化呈现一定程度降低趋势(BC段斜率略小于AB段斜率)，这是由于随着断层位移增长，土与隧道接触范围土的塑性区逐渐增加，土与隧道之间的相互作用力有所减弱，因此，结构响应增长趋势有所降低。

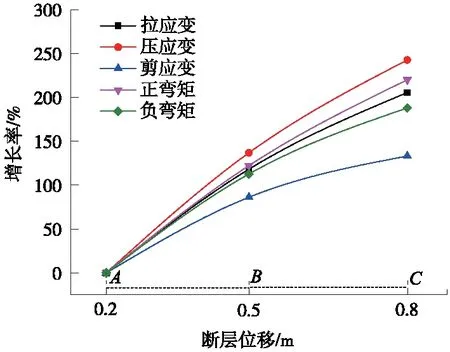
图11 结构响应增长率变化趋势

2.2 土-隧道摩擦系数

其他参数不变，数值模拟中土-隧道之间的法向行为设置为“硬”接触，切向行为为库伦摩擦，摩擦系数分别为0.24、0.6、0.96时(工况1、4、5)，隧道纵向拉压应变极值见图12。与工况1对比，工况4、5拉应变最大值分别增加了6.1%、6.9%；压应变最大值分别增加了4.1%、4.9%。隧道剪应变见图13，与工况1对比，工况4、5最大值剪应变分别增加了7.9%、9.5%。沿隧道轴向截面弯矩极值见图14，与工况1对比，工况4、5正弯矩最大值分别增加了4.6%、5.2%；负弯矩最大值增加了4.4%、5.1%。由以上分析可知，随着土-隧道摩擦系数增大，土-隧道之间越难发生相对滑动，断层位移越大，隧道结构位移越大，相应的结构响应逐渐增大。

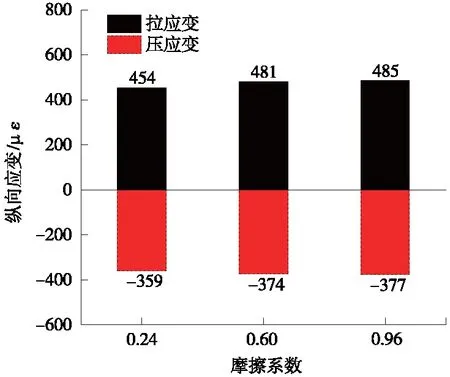
图12 不同土-隧道摩擦系数纵向应变极值

图13 不同摩擦系数剪应变云图(单位：ε)

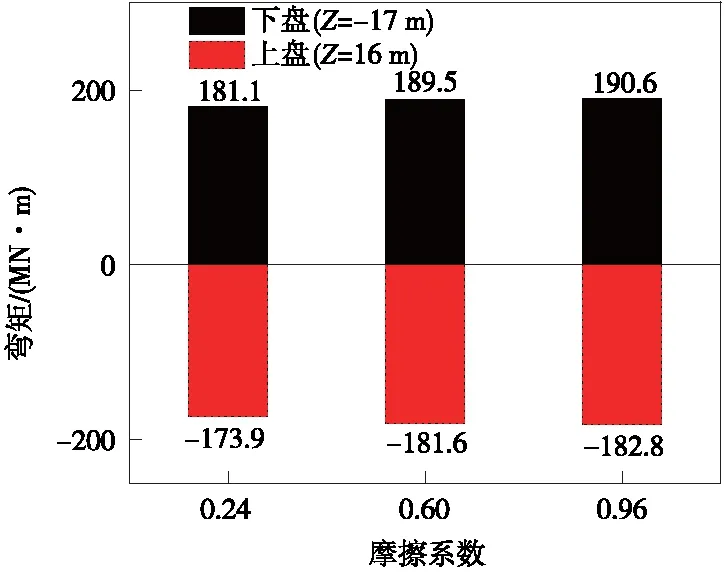
图14 不同摩擦系数弯矩极值

各指标结构响应增长率变化趋势见图15。由图15可知，当摩擦系数由0.24变为0.6时，各指标的增加变化较大(AB段)，当摩擦系数由0.6变化到0.96时，各指标最大值略有增加，但增加幅度趋于稳定(BC段)。这是因为当摩擦系数足够大时，土与隧道之间很难发生相对滑动。因此，当摩擦系数由0.6变化为0.96时，各指标最大值变化并不明显。由以上分析可知，随着土-隧道摩擦系数增加，结构响应呈对数增长。

图15 结构响应增长率变化趋势

2.3 隧道埋深

其他参数不变，土层埋深分别为7.5，10，12.5 m时(工况3、6、7)，隧道纵向拉压应变极值见图16。与工况3对比，工况6、7拉应变最大值分别增加了11.1%、22.2%；压应变最大值分别增加了-0.3%、9.4%。隧道剪应变见图17，与工况3对比，工况6、7剪应变分别增加了2.4%、19.8%。沿隧道轴向截面弯矩极值见图18，与工况3对比，工况6、7正弯矩分别增加了5.6%、16.2%；负弯矩分别增加了1.8%、12.9%。由以上分析可知，随着隧道埋深增加，隧道响应逐渐增加。

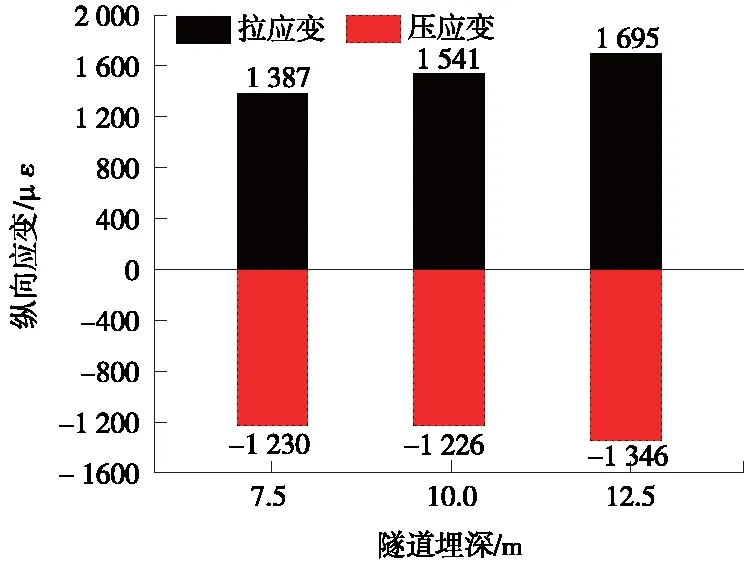
图16 不同隧道埋深纵向应变极值

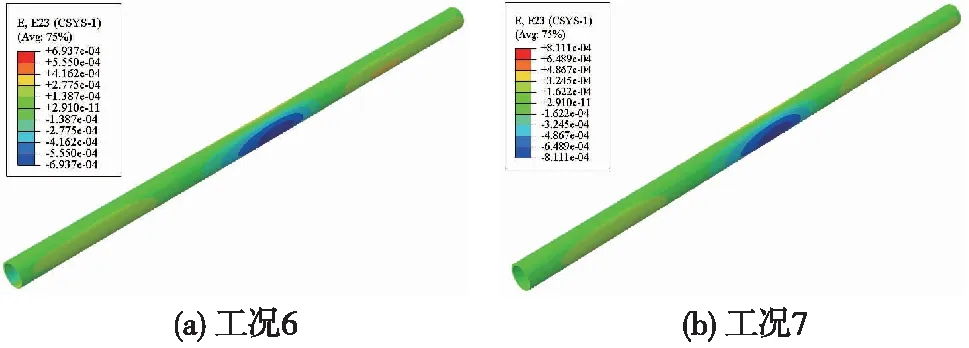
图17 不同隧道埋深剪应变云图(单位：ε)

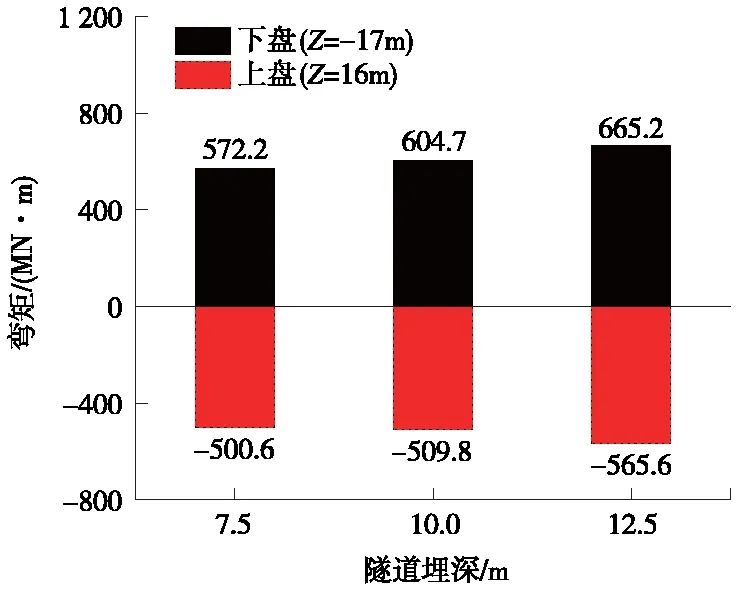
图18 不同隧道埋深弯矩极值

各指标结构响应增长率变化趋势见图19。由图19可知，随着隧道埋深增加，结构响应增长率显著增加(AB段斜率小于BC段斜率)。工况3土层竖向位移云图见图20(位移荷载施加方法见图2)。由图20可知，随着隧道埋深增加，剪切带宽度逐渐变窄，隧道所遭受的强制位移逐渐增大，结构响应逐渐增大。结构埋深越大，越靠近断层错动点，断层错动产生的能量以非线性形式增加，结构响应呈指数增长。

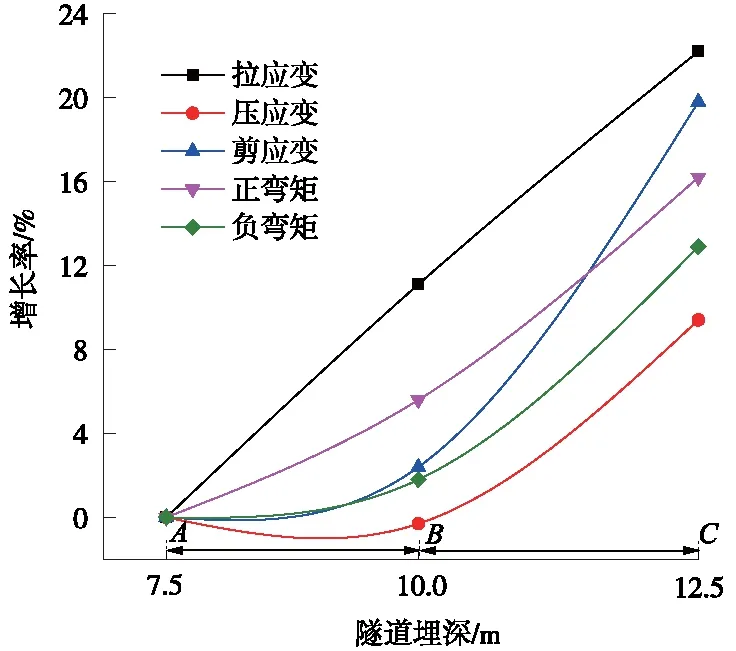
图19 结构响应增长率变化趋势

图20 工况3正断层错动迹线

3 结构变形与损伤分析

由第2节分析可知，当混凝土结构采用弹性模型时，能较好地反映出不同参数的影响规律及增长率变化趋势。但弹性结构模型无法考虑混凝土衬砌在塑性阶段的刚度退化，也无法量化表达出衬砌结构的破坏。ABAQUS中混凝土塑性损伤模型以LUBLINER[20]和LEE and FENVES[21]提出的损伤模型为基础，可模拟混凝土材料的拉裂和压碎等力学现象，且在断层错动分析中有所应用[22]。因此，采用混凝土塑性损伤模型进行正断层错动作用下隧道结构损伤分析，衬砌选用为国内常用的C30等级混凝土，密度为2 500 kg/m3，弹性模量30 GPa，泊松比0.25，塑性损伤参数见表3，数值模型其他参数保持不变。

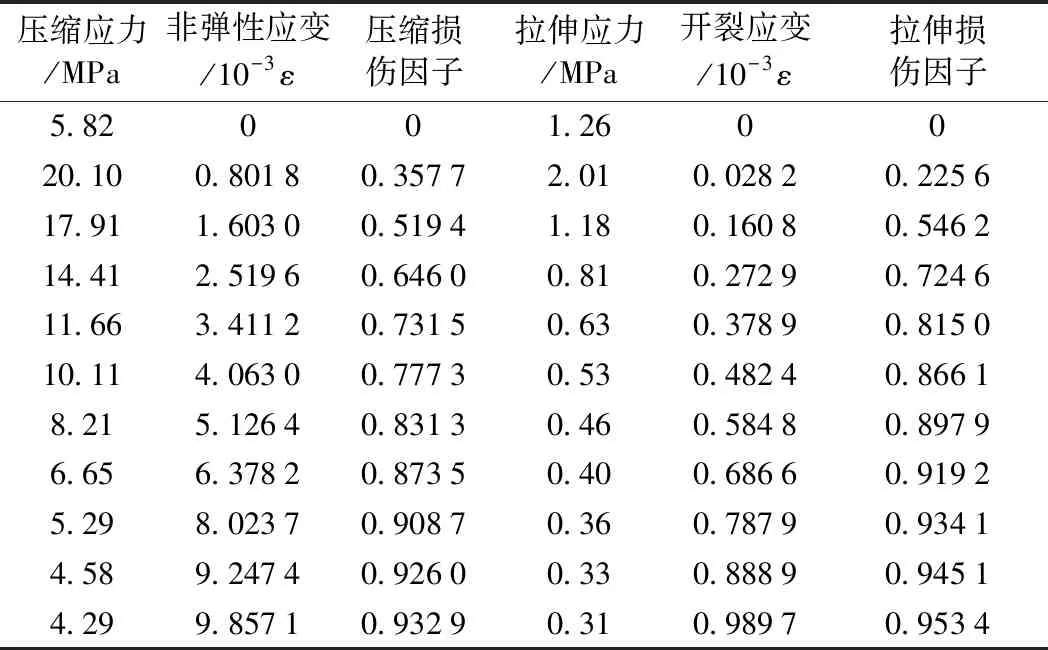
表3 混凝土损伤参数(C30)

3.1 隧道纵向与横向变形

施加正断层竖向位移0.2 m，相应的水平位移为0.073 m。隧道拱顶竖向位移沿隧道轴线分布见图21。断层错动发生后，隧道衬砌沿着纵向发生了“S”状弯曲，上盘内隧道受竖向位移的作用，二次衬砌产生向下位移0.2 m。产生这种现象的原因是，模型断层下盘固定，对整个上盘施加强制位移，因此，造成错动处相对位移最大，沿隧道轴向两侧逐渐减小，隧道在强制位移的作用下变为“S”形。

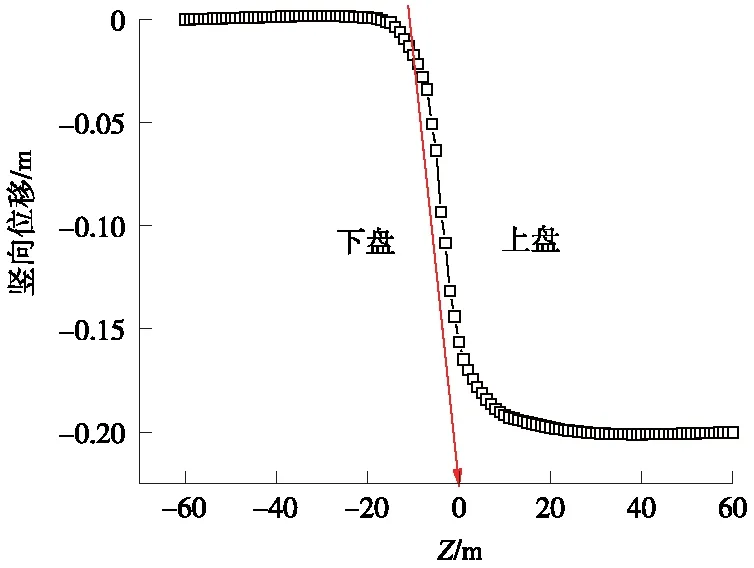
图21 隧道拱顶竖向位移沿纵向分布曲线

隧道横截面变形以隧道椭圆度表示(图22)，椭圆度计算方法为

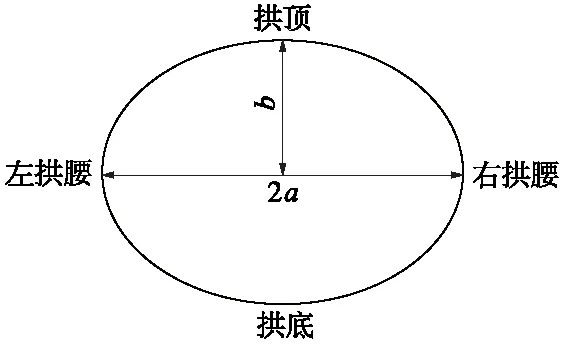
图22 隧道椭圆度计算示意

T=2×(a-b)/D

(1)

式中，T为椭圆度；a为隧道长半轴；b为隧道短半轴；D为隧道外径。

依据式(1)，得到沿轴向隧道椭圆度分布曲线，见图23。最大椭圆度出现在纵向坐标-5 m处，最大值为15.22‰。盾构隧道验收规范要求椭圆度最大限制不得超过5‰[23]，因此，对于现浇式混凝土隧道而言，其限值应不大于5‰。由以上变形分析可知，隧道在断层错动作用下横截面变形已超过容许值，可能发生变形破坏。

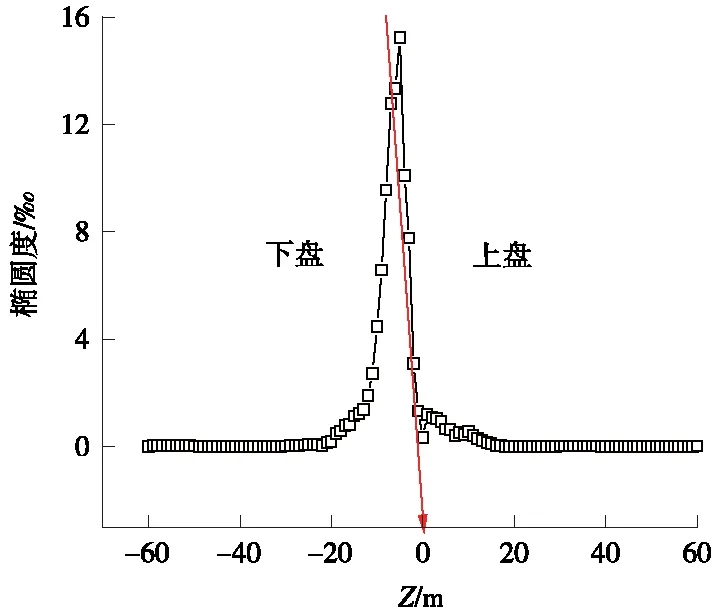
图23 沿纵向隧道椭圆度分布曲线

3.2 损伤分析

3.2.1 等效塑性应变

ABAQUS中的断层错动作用下隧道结构等效塑性应变(PEEQ)分布见图24。隧道等效塑性应变沿上盘拱顶向下盘拱底分布，等效塑性应变最大值出现在纵向坐标-5 m拱腰处。由图23可知，在纵向坐标-5 m处，隧道椭圆度最大，产生应力集中，因此等效塑性应变在此处达到最大。

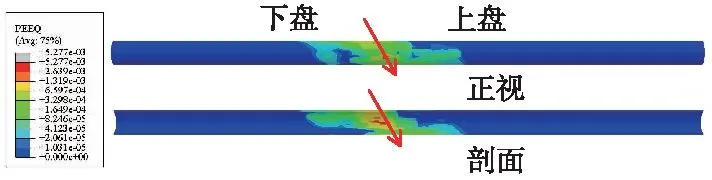
图24 等效塑性应变云图(单位：ε)

3.2.2 拉压损伤分析

断层错动作用下隧道拉压损伤因子分布见图25。表3中C30级混凝土衬砌达到极限抗拉抗压强度分别为2.01，20.1 MPa时，对应的拉压损伤因子分别为0.225 6与0.357 7。在ABAQUS中对所有衬砌“element”建立“display group”，再利用“query”功能可得到网格各单元的受拉损伤因子。定义受拉损伤因子≥0.225 6单元为受拉损伤单元，受压损伤因子≥0.357 7单元为受压损伤单元。则受拉损伤体积为146.47 m3，受压损伤体积为13.5 m3，受拉破坏范围大于受压破坏范围。

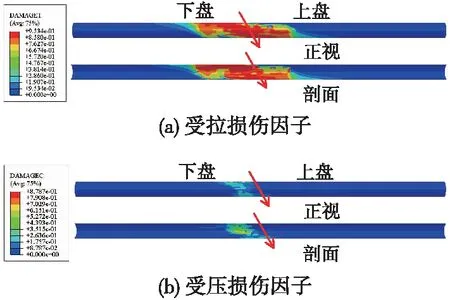
图25 拉压损伤因子分布云图

依据CHEN等研究，混凝土裂缝可通过拉伸损伤因子计算[24]。

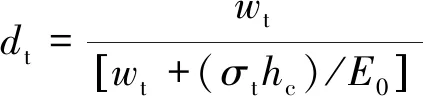
(2)

式中，hc为特征值长度，对于八节点积分单元而言等于单元边长[25]，σt为拉应力，E0为初始弹性模量。

以混凝土裂缝宽度限值0.2 mm为标准[26]，由式(2)计算得到对应的损伤因子为0.949。结合以上分析，依据损伤因子将二次衬砌破坏等级划分见表4。

表4 二次衬砌破坏等级划分

3.2.3 剪切破坏分析

衬砌环内剪应变分布见图26，剪应变沿隧道轴线两侧对称分布，最大剪应变出现在拱腰处，最大剪应变值为12 900 με。

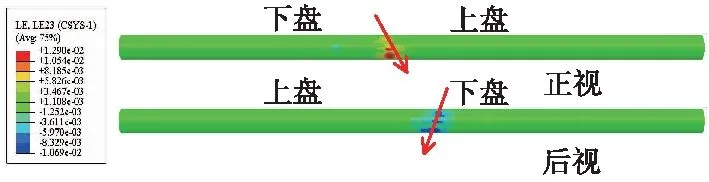
图26 隧道剪应变云图(单位：ε)

混凝土允许的极限剪切应变

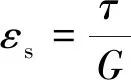
(3)

式中，τ为混凝土抗剪强度，τ=c×σcu，σcu为混凝土抗压强度，c为常数，一般取为0.095～0.121[27]；G为混凝土剪切模量，G=0.4E0，为混凝土弹性模量[28]。

由式(3)计算得到混凝土允许的最大剪切应变为202.7 με，图26拱腰处剪应变最大值为12 900 με，远大于允许的极限剪切应变202.7 με，表示混凝土极可能发生了严重的剪切破坏。

4 结论

建立三维有限元模型并与离心机试验对比，验证了数值模拟的合理性。对正断层浅埋隧道断层位移、土-隧道摩擦系数、隧道埋深进行了参数分析，重点研究了不同参数对结构响应增长率变化的影响。采用混凝土损伤模型从变形和损伤两方面定量表达了隧道结构的破坏，得到以下结论。

(1)随着断层位移增加，结构受到的强制位移增加，结构响应基本呈线性增长；土-隧道摩擦系数越大，隧道结构越难与土层发生相对滑动，结构响应呈对数增长；隧道埋深越深，断层错动产生的能量以非线性形式增加，隧道响应呈指数增长。

(2)从变形角度而言，正断层错动黏滑作用下，断层错动面处土体产生的相对位移最大，隧道结构沿纵向发生“S”形变形。圆形断面隧道受到覆土压力与断层位移的共同作用，逐渐变为椭圆形，拱腰处产生应力集中，塑性损伤最大。当椭圆度超过允许值时，结构可能发生变形破坏。

(3)正断层错动作用下，错动面处结构在土体强制位移的作用下，可能发生拉压剪共同破坏。基于混凝土塑性损伤模型，通过拉伸损伤因子计算混凝土裂缝宽度，可将衬砌结构的开裂程度划分为无破坏、轻微破坏、中等破坏及严重破坏4个等级。隧道结构受拉损伤体积大于受压损伤体积，隧道剪切破坏可通过与环内剪应变极限值对比判断。隧道椭圆度判别、拉裂程度等级划分及剪切破坏判别可为工程设计中定量分析提供参考。