基于矢量阈值分解的新型MCFR-DPD方案

王晶琦,陶 詹,王新浩,吴 文

(南京理工大学 电子工程与光电技术学院,江苏 南京 210094)

对于功率放大器来说,功率效率和线性度是一对极难调和的矛盾。正交频分复用(Orthogonal frequency division multiplexing,OFDM)技术被广泛应用于无线通信系统中,但OFDM信号高峰均比[1]的特性进一步加剧了功率放大器功率效率与线性度之间的矛盾[2]。在当今无线通信系统中,设计高效率和高线性度的射频功率放大器成为了亟待解决的关键技术[3]。

峰值因子降低(Crest factor reduction,CFR)技术的原理在于减小信号峰值从而降低信号的峰均比(Peak to average power ratio,PAPR),信号峰均比降低后功放在平均功率工作点对输出峰值功率进行回退的值就可以降低,从而提高了功放效率。数字预失真[4](Digital predistortion,DPD)技术是一种有效的在高效率区补偿功放的非线性和记忆效应的方法。

不少文献考虑将数字预失真技术与峰值因子降低技术相结合使用,从而实现同时提高功放效率和线性度的目的。文献[5]提出两种降低峰均比的方法来改善高功率放大器的功率效率,虽然两种降低峰均比的方法都能降低峰值功率,但不足以抑制带外辐射,因此考虑引入预失真技术限制频谱再生从而改善系统整体的非线性。文献[6,7]将CFR模块应用于DPD模块之前,提高线性化的有效性,并且减少功率的回退从而增加效率。文献[8]提出了一种结合高速数字时域发射机均衡和高速DPD的线性化技术。为了提高动态非线性模型对宽带系统建模的精度,又提出了一种基于记忆多项式的动态非线性模型。为了避免经DPD之后信号峰均比再次变大从而可能导致功放被过驱动,需要在DPD模块之后加一个包络削波模块[9]。以上基于CFR和DPD相结合的方案都是将CFR模块独立应用于DPD模块之前[10],系统都有较高的运行复杂度,鉴于此,一种模型化峰值因子降低-数字预失真(Modeled crest factor reduction-digital predistortion,MCFR-DPD)联合模块化的技术[11]被提出,MCFR模块应用于DPD模块的输出信号,最终的效果相当于在DPD系数中引入稳态偏移来降低预失真后信号的峰值,此方案有效地将DPD模块、CFR模块和包络削波模块组合成一个模块[9]。在以上工作的基础上,本文分析了CFR和DPD模块各自的特性,对输入信号进行矢量阈值分解,提出了基于矢量阈值分解的新型MCFR-DPD方案,降低了削峰对系统DPD效果的抑制影响,从而提高了系统的线性度。

1 数字预失真与峰均比降低

1.1 数字预失真技术

预失真技术即在功率放大器之前增加与其特性相反的非线性系统[12,13],来补偿功率放大器的非线性特性。预失真技术原理如图1所示。

图1 预失真原理图

数字预失真核心研究内容即如何构建高精度预失真器行为模型,本文对数字预失真器建模选用记忆多项式[14,15](Piecewise memory polynomial,PMP)模型。

间接学习结构不需要对功放行为模型进行建模,并且可采用常见的线性滤波算法[16]进行模型参数的提取,实现思路简单,因此本文基于间接学习结构来提取预失真器系数,数字预失真技术中预失真器参数的提取[2]选择在软件上易于实现的最小二乘(Least square,LS)算法。

1.2 峰均比降低技术

信号的峰均比是指信号的峰值功率与平均功率的比值。信号的PAPR降低技术,主要可分为三大类:预畸变类技术、编码类技术、概率类技术[17,18]。信号预畸变类技术,比如直接限幅、限幅滤波,是最早提出来的一种抑制峰均比的技术,也是最简单直观和有效的峰均比抑制技术[19]。考虑到技术复杂度与实现难度,本文选择最简单的直接限幅。对输入信号x(n)进行直接限幅操作,限幅后的信号表示为

(1)

式中:A=CR·σ是限幅的门限值,也即信号的阈值,B(n)为复信号x(n)的相位,CR为限幅率,σ为信号功率的均方根,高于阈值部分的信号记为Cclip(n)=x(n)-xHC(n)。

1.3 传统的峰均比降低技术与预失真技术结合方案

功率放大器(Power amplifier,PA)的功率效率和线性度取决于其工作点。高效率通常对应于差的线性度。为了优化效率/线性度权衡,CFR技术通常与DPD一起实施,以控制PA工作点[20]。经典的峰均比降低技术与预失真技术相结合的方案是将CFR模块与DPD模块级联起来使用[21,22]。CFR模块的目的是降低输入信号的峰均比。功率放大器作为非线性器件,当其工作在非线性区时会呈现出增益压缩的特性,越接近饱和区,增益压缩得越严重。作为功放逆模型的数字预失真器势必会对输入在非线性区的信号进行增益扩张,以补偿后面级联的功放将引起的压缩增益。经典的CFR与DPD相结合的方案中DPD模块在CFR模块之后应用,这使得削峰后PAPR降低了的信号经过DPD峰均比再次增大。为了防止功率放大器被高PAPR信号过驱动造成损伤,功率放大器设计时应该对高峰值信号承受能力留有一定裕量,设置的最大承受的信号PAPR应该包括这个裕量。通常在DPD模块后加一个包络削波模块,如图2所示,输入功率放大器的信号的PAPR如果超过设定的PAPR的阈值,则会被包络削波模块削掉超出的部分。

图2 加入包络削波模块的CFR与DPD结合方案

以上传统的CFR与DPD结合的方案中,CFR模块往往独立应用于DPD模块之前,系统的运行复杂度较高。文献[9]提出一种CFR-DPD联合模块化的方案,削峰针对预失真后的信号,CFR模块采用非线性系统建模的方式进行,并且对CFR模块建模选用与DPD模块相同的模型基函数,称为MCFR模块。此方案将MCFR模块、DPD模块以及包络削波模块有机地整合为一个模块,大大降低了系统的运行复杂度。但是该方案在应用时忽略了CFR技术的物理意义,使得MCFR模块对预失真后原本不需要进行削峰的部分输入信号也进行了处理,引入了不必要的失真,导致系统线性化效果变差。针对这一问题,本文提出了基于矢量阈值分解的新型MCFR-DPD方案。

2 基于矢量阈值分解的新型MCFR-DPD方案

2.1 传统MCFR-DPD技术联合模块系数提取

传统MCFR-DPD技术联合模块系数的提取方法如图3所示,CFR模块针对预失真后的信号,也即对DPD之后的信号直接进行限幅处理,假定超出设定的阈值的那一部分信号为Cclip,建模时输入信号仍选用系统的输入,对MCFR模块以非线性系统行为建模的方式进行,选用的模型与DPD选用的模型一样,只有这样才是真正意义上的将DPD模块与CFR模块整合为一个模块。

图3 MCFR-DPD技术的联合模块系数提取方法

假设提取的没有经过峰值因子降低的预失真信号对应的DPD系数为A=[a10,…,aK0,…a1Q,…,aKQ]T,经过峰值因子降低后超出设定的阈值A的那一部分信号Cclip对应的MCFR模块的系数为B=[b10,…,bK0,…b1Q,…,bKQ]T,其中K为MP模型非线性阶数,Q为MP模型记忆深度,则MCFR-DPD联合模块的系数θ=A-B。

由上述分析,MCFR-DPD联合模块的系数θ=A-B相当于在提取的DPD系数中引入稳态偏移,最终可以实现降低预失真后信号也即功放输入信号峰均比的目的。方案中模块的系数提取均可以离线进行,因此,联合方案的运行复杂度与只进行DPD的系统复杂度相当,只是多了一些系数的减法运算,与以往经典的CFR模块与DPD模块独立应用的方案相比降低了运行复杂度。

本文进一步对传统MCFR-DPD技术进行分析,发现该技术仅将CFR和DPD简单结合,并未考虑两者间相互影响。在对MCFR进行建模时,输入信号使用的是全部幅度范围的输入信号,但从CFR技术的物理意义考虑,直接限幅方法应只影响大于削峰阈值的相应部分输入信号,传统联合方案中的CFR模块会对小于阈值的输入信号引入不必要的失真,从而降低DPD模块的线性化效果。鉴于此,本文考虑将输入信号进行分段,将DPD模型和CFR模型都分解为分段式模型,将直接限幅引入的带内和带外误差限制在信号幅值较大的分段区间,也即非线性较为严重的区域,不让其对小于阈值的弱非线性区域的信号产生影响,这样做可以将削峰对系统DPD效果的抑制影响尽可能降低,从而提高系统的线性度。

2.2 矢量阈值分解技术

模型构建和使用过程中,经常用到信号分段技术。传统的分段方法,是将输入信号按阈值幅度划分,大于阈值幅度的信号为大信号,小于阈值幅度的信号为小信号,为保证两组信号个数与原信号一致,大信号中原本小于等于阈值的部分和小信号中原本大于阈值的部分都被赋零,如图4所示。这种分段方法直观且简便,但两组信号在阈值分界处都有突变,应用到DPD建模中,常导致输出信号在分界处出现跳变。

图4 传统分段方法

矢量阈值分解技术,其阈值以复信号平面的一个矢量圆的形式出现,分解信号时,将小信号中原本大于阈值部分的幅度赋为阈值幅度,其相位保持原信号相位不变,而大信号部分则直接复制为原信号与阈值的差值,其相位信息依然保持不变,如图5所示。经过矢量阈值分解后的信号,不仅在幅度上避免了大幅突变,更得以保留其相位信息,对其进行分段模型建模,可避免出现输出跳变的情况。

图5 矢量阈值分解方法

在对预失真模块以及削峰模块建模前应当先确定好模块建模所需要的分段阈值。本文主要涉及的阈值有两个,一个是分段DPD的阈值th1,另一个是CFR削峰的阈值th2。其中,分段DPD的阈值主要根据功放AM/AM特性图中线性与非线性的临界点来决定,通常取其切线斜率变化处[23]。而CFR削峰的阈值则需要结合本文方案进行综合考虑。

本文所提方法仅对DPD矢量阈值分解后的大信号部分(即大于th1的信号)进行CFR处理,小信号部分与CFR无关,因此,从原理上应保证th2≥th1。而由于DPD模块本身为非线性模块,经过DPD模块后的信号会有失真,其峰均比与原始输入信号不同,因此,在选择th2时须考虑DPD模块引起的畸变。图6为DPD模块的AM/AM曲线。图中所取点的x坐标即为th1。本文选取输入th1时对应的模块输出幅度为th2,这样可以保证所有的大信号都进行CFR处理,而小信号不会受其影响。

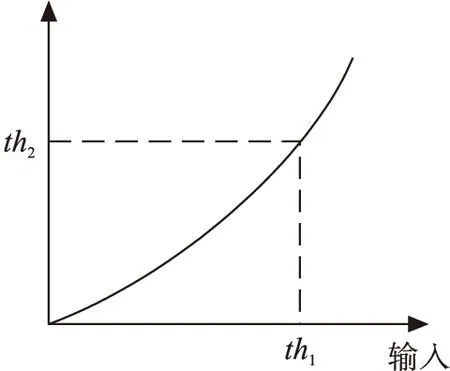
图6 DPD模块的AM/AM曲线

2.3 基于矢量阈值分解的新型MCFR-DPD方案

本文基于矢量阈值分解技术,将输入信号分为两段,分段后的两个子信号分别为大信号x1(n)和小信号x2(n),设分段阈值为实数λ,分解后的子信号如下

(2)

(3)

式中:|x(n)|是x(n)的幅度值,φ为x(n)的相位。

图7 基于矢量阈值分解的新型MCFR-DPD方案应用框图

基于矢量阈值分解的新型MCFR-DPD方案的结构框图如图7所示。

基于矢量阈值分解的新型MCFR-DPD方案的方案流程图如图8所示。

图8 方案流程图

设上述分段后的两个子信号为xs(n),s=1和2,预失真后对应的子信号为

(4)

式中:xs(n)和zs(n)分别表示子信号的输入和输出,将其表示为矩阵形式如下

ZS=XSAS

(5)

最终的输出是

z(n)=z1(n)+z2(n)

(6)

表示为矩阵形式则为

(7)

系数的提取用最小二乘法,最小二乘解为

A=(XHX)-1XHZ

(8)

根据上述LS算法可以求出预失真器系数A=[A1,A2]T,然后可以得到矢量阈值分解后的输入信号经过数字预失真后的输出信号z(n),计算出限幅阈值,对其进行直接限幅。由于限幅阈值th2≥分解阈值th1,超出限幅阈值部分的信号Cclip只会与经过矢量阈值分解后的大信号x2(n)有关,即MCFR模块的系数提取是以矢量阈值分解的第二组信号x2(n)为输入,以经过预失真后信号超出限幅阈值部分的信号Cclip为输出而进行的,假设其提取到的系数矩阵为B,那么最终分段后得到的联合CFR-DPD模块的系数θ=[A1,A2-B]T。

将输入信号分成两段后,基于矢量阈值分解的新型MCFR-DPD方案实现流程如下:

(1)基于原始输入信号,进行矢量阈值分解,得到x1(n),x2(n);

(2)设置合适的非线性阶数K,记忆深度Q,基于式(7)和式(8)得到每一段输入对应的预失真系数A1,A2;

(3)分段后的输入信号经过预失真器,得到其对应的输出z1(n),z2(n),预失真后整体的信号z(n)=z1(n)+z2(n),根据DPD模块特性计算出限幅阈值th2;

(4)对预失真后的整体信号z(n)进行直接限幅;

(5)根据限幅前后的信号计算得到Cclip;

(6)基于分段后的第二段输入信号x2(n)与Cclip提取出MCFR的系数B;

(7)计算出联合CFR-DPD模块的系数θ=[A1,A2-B]T;

3 仿真结果对比分析

3.1 仿真参数设置

为了评估本文所提出的基于矢量阈值分解的新型CFR-DPD方案的性能,在MATLAB中对其进行仿真分析,测试输入信号选择带宽为10 MHz、采样频率为122.88 MHz的LTE信号,信号的峰均比为6.62 dB,用6个抽头的线性滤波器和Saleh模型级联而成的Hammerstein模型模拟待测的功率放大器,选用非线性阶数为5,记忆深度为3的MP模型作为预失真器模型。基于矢量阈值分解技术,将信号分成两段进行处理,取0.8为归一化输入信号幅度的分界点,对预失真器进行建模。

3.2 削峰效果对比

建模后对输入信号进行预失真,预失真后信号的PAPR变大,变为10.07 dB。选取限幅比CR=2.5,对预失真后的信号进行限幅,即目标PAPR=7.96 dB。按照2.3节基于矢量阈值分解的新型MCFR-DPD方案的实现流程,得到联合CFR-DPD模块的输出,也即功放的输入信号的PAPR为8.33 dB,削峰后信号的峰均比降低了1.74 dB。而传统MCFR-DPD方案,未对预失真后的信号进行削峰时PAPR为10.22 dB。同样的,选取限幅比CR=2.5,削峰后的信号,也即功放的输入信号的PAPR为9.06 dB,信号的峰均比降低了1.16 dB。

为了能够清晰直观地看出两种方案下削峰效果的对比,现将两种方案经过联合CFR-DPD模块处理过的时域信号在一张图上表示,如图9所示,为了方便观察,只选取了5 100到5 500时刻的时域信号。

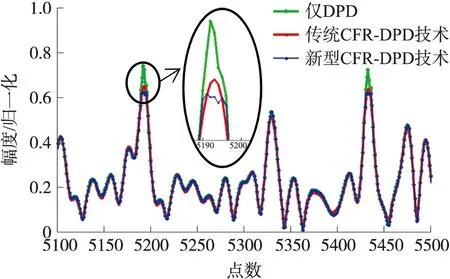
图9 削峰效果时域对比图

图中绿色的曲线表示基于矢量阈值分解技术仅对输入信号进行预失真处理,预失真后的信号在时域上的幅值,蓝色的曲线表示采用基于矢量阈值分解的新型MCFR-DPD方案预失真信号削峰后在时域上的幅值,红色的曲线表示传统MCFR-DPD方案预失真信号削峰后在时域上的幅值。从图中可以看出新方案的削峰性能最好,峰值下降最明显。但由于PMP模型无法完美拟合CFR过程,放大峰值区域可看到削峰后仍剩余小幅波动,从后续DPD效果对比可以看出,这类局部区域的不光滑现象并不影响整体CFR-DPD的效果,可以忽略。

另一方面,采用互补累积分布函数(Complementary cumulative distribution function,CCDF)去衡量峰均比分布情况,如图10所示。

图10中紫色的曲线是输入信号峰均比分布情况,经过DPD之后信号的PAPR会增大,绿色的曲线即表示基于矢量阈值分解技术对输入信号进行DPD处理后的信号峰均比分布情况,预失真后信号的峰均比变为10.07 dB;蓝色的曲线表示采用基于矢量阈值分解的新型MCFR-DPD方案预失真信号削峰后峰均比分布情况,预失真信号削峰后信号峰均比变为8.33 dB;红色的曲线表示传统MCFR-DPD方案预失真信号削峰后峰均比分布情况,预失真信号削峰后信号峰均比变为9.06 dB。从图9、图10中可以清晰地发现基于矢量阈值分解的新型MCFR-DPD方案在削峰有效性方面优于传统MCFR-DPD方案。这是因为CFR-DPD联合模块化技术对MCFR模块进行系数提取时输出信号是预失真后信号的削峰噪声Cclip,当输入信号为全部信号时,PMP模型无法精准拟合CFR模块的特性,而本文所提的分段方案中,模型输入信号经过矢量阈值分解后,大部分为零值,仅小部分为有效信号,这与模块输出的削峰噪声实际情况相吻合,PMP模型的拟合精度得以大幅提高,因此基于矢量阈值分解的新型MCFR-DPD方案与传统的MCFR-DPD方案相比削峰效果有显著提高。

图10 两种方案下削峰性能对比图

3.3 线性化效果对比

以上分析了基于矢量阈值分解的新型MCFR-DPD方案的削峰效果,下面对其线性化效果进行评估。根据2.3节方案实现流程,经过步骤3)得到未经削峰仅经过预失真处理的功放输出信号的ACPR,高频处(Upper)为-42.10 dBc、低频处(Lower)为-41.21 dBc;经过步骤(9)得到基于矢量阈值分解的新型MCFR-DPD方案功放输出信号的ACPR,高频处(Upper)为-39.79 dBc、低频处(Lower)为-40.06 dBc,与传统MCFR-DPD方案相比,系统线性化性能得到大幅改善,功放输出信号的ACPR在高频处(Upper)改善了5.98 dB、低频处(Lower)改善了6.17 dB。即使与不削峰仅做DPD处理的方案相比,新型MCFR-DPD方案的线性化效果依然可观,说明新型MCFR-DPD方案有效降低了削峰对系统DPD效果的抑制影响。预失真过程中功放输出信号的功率谱密度如图11所示。

图11 预失真效果对比图

此处需要说明的是,图11中绿色曲线表示的是基于矢量阈值分解技术仅对输入信号经过预失真处理,功放输出信号功率谱密度,黑色的曲线表示原始输入信号经过功放后输出信号功率谱密度,蓝色的曲线代表采用基于矢量阈值分解的新型MCFR-DPD方案功放输出信号功率谱密度,红色的曲线代表传统MCFR-DPD方案功放输出信号功率谱密度,从图上可看出新型MCFR-DPD方案功放输出信号的线性度比仅DPD的方案略差一些,但与传统MCFR-DPD方案相比,线性化效果有大幅提升。

3.4 不同限幅比对方案的影响

此外,本文考虑了不同限幅比对基于矢量阈值分解的新型MCFR-DPD方案的影响,选择限幅比CR=2,测试基于矢量阈值分解的新型MCFR-DPD方案的削峰效果以及线性化效果,并与前面限幅比CR=2.5时进行对比,具体数值对比如表1、表2所示。

表1 选取不同限幅比CR时,基于矢量阈值分解的新型MCFR-DPD方案削峰效果比较

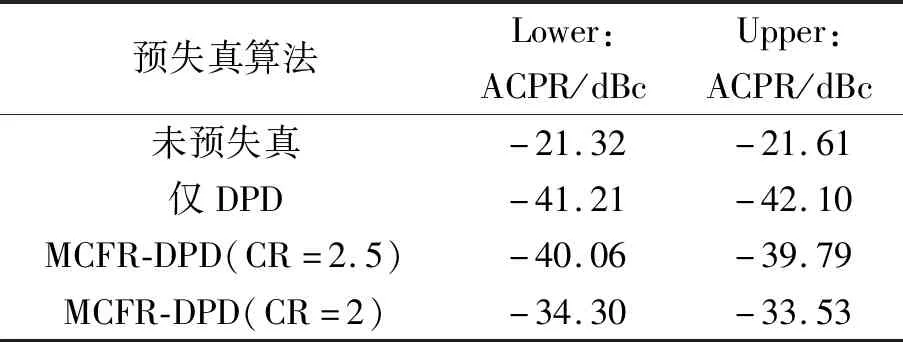
表2 选取不同限幅比CR时,基于矢量阈值分解的新型MCFR-DPD方案线性化效果比较

通过表1、表2中的数值比较不难发现,限幅比不同,那么最终的削峰效果以及线性化效果也就不同,并且限幅比选取越小,也即限幅程度越大,信号的峰均比降得越多,但同时线性化效果变差,实际应用时需要结合具体情况权衡线性化效果与削峰效果选择合适的限幅比CR。

通过对比不同情况下MCFR-DPD联合方案最终的削峰效果与线性化效果,可以发现基于矢量阈值分解的新型MCFR-DPD方案不论是削峰效果还是线性化效果都要优于传统MCFR-DPD方案。实际应用基于矢量阈值分解的新型MCFR-DPD方案可以通过选择不同的限幅比CR来实现削峰效果以及线性化效果的权衡。

4 结论

本文对数字预失真技术与峰均比降低技术的结合进行了研究。传统的数字预失真技术与峰均比降低技术结合方案一般都是在DPD模块之后附加包络削波模块,这样做不仅增加了系统复杂度,而且可能导致使用自适应滤波算法来提取预失真器系数时出现不收敛的情况。针对传统结合方案中存在的问题,出现了CFR-DPD联合模块化技术,通过引入多项式模型化的CFR模块并将其应用于DPD模块的输出,来实现将CFR模块与DPD模块的整合使用。本文引入阈值分解技术对CFR-DPD联合模块的建模采用分段MP模型,提出了基于矢量阈值分解的新型MCFR-DPD方案,仅对小信号进行模块化CFR处理,以降低联合模块中CFR对DPD线性效果的影响。仿真结果表明,与传统未经分段的MCFR-DPD方案相比基于矢量阈值分解的新型MCFR-DPD方案有着更好的削峰效果以及线性化效果。