基于SPA-LSSVM的混合农药残留荧光检测建模方法
王晓燕,季仁东,韩 月,卞海溢,杨玉东,蒋喆臻,冯小涛,徐江宇
(淮阴工学院 江苏省湖泊环境遥感技术工程实验室,江苏 淮安 223001)
农药残留是影响生态环境及食品安全的重要因素,目前针对农药残留的检测主要应用气相色谱法[1]、高效液相色谱方法[2]、色谱-质谱联用方法[3]、免疫分析方法[4]、酶抑制方法[5]、生物传感器方法[6]以及光谱方法等[7,8]。荧光检测属于光谱方法中的一种,它具有检测速度快、灵敏度高、操作简便等优点,常用于农药残留的检测及分析[9,10]。
农药残留的定量分析通常应用偏最小二乘法[11](Partial least square,PLS)、支持向量机方法[12]以及神经网络[13]等方法,其中,偏最小二乘法是化学计量学中应用最广泛的校正方法之一,其综合了主成分分析和典型相关分析的优势,在基于光谱对农药残留的定量分析中具有较好的预测性能。支持向量机方法通过应用结构风险最小化原理提高模型的泛化能力,能够较好地解决小样本问题,它通过非线性变换将原始变量映射到高维特征空间,并在高维空间中进行线性处理,从而避免出现维数灾难问题[14,15]。
目前,针对混合农药残留的定量分析中,PLS方法仍是主流方法,文献[16]基于表面增强拉曼光谱应用PLS方法对脐橙表面的混合农药(亚胺硫磷和乐果)进行检测分析,获得了较好的含量预测结果。文献[17]基于荧光光谱采用神经网络方法对速灭威和西维因两种成分的混合农药进行定量分析,并分别比较了全光谱和遗传算法获取特征光谱两种情况下的预测性能,结果显示,遗传算法优选出特征波长后对应的BP神经网络模型具有更高的预测精度。文献[18]基于荧光光谱研究4种成分混合农药的含量预测,应用支持向量机方法在全波长情况下对各成分进行了定量分析。在农药残留的荧光检测及分析建模中,支持向量机方法结合全光谱往往能够取得较高的分析精度,但基于全波段的支持向量机模型也存在训练时间长、运算复杂、冗余度高等不足。若首先针对荧光光谱进行特征选择,优选出较显著的特征波长点,然后基于特征光谱建立支持向量机模型,则可大大加快训练速度,获得更加简单实用的特征光谱模型。
本文提出了一种基于连续投影算法(Successive projections algorithm,SPA)和最小二乘支持向量机(Least squares support vector machines,LSSVM)的分析方法,用于混合农药残留的含量预测。应用连续投影方法优选出荧光特征波长,并基于最小二乘支持向量机方法建立多组分定量分析模型,以期获得优于传统偏最小二乘方法的预测精度。
1 SPA-LSSVM算法原理
1.1 连续投影算法
在光谱分析中应用SPA方法选择特征波长的原理为:首先将原始波长中的某一个波长点选中,然后分别计算出该波长在其它剩余未被选中波长上的投影,再将其中投影向量最大的波长点筛选到特征波长组合中,依次共筛选完成所需个数的特征波长后结束计算[19,20]。
若将光谱属性矩阵记为XM×J(M为样本数,J为波长个数),Xk(0)代表初始波长向量,需要筛选的特征波长个数设为N,则SPA的实现步骤为
(1)在迭代开始前(n=1),任选一个光谱属性矩阵X中的某一列向量xj,记作Xk(0);
(2)将其它未被选中的波长变量集合记为set,set={j,1≤j≤J,j∉{k(0),k(1),…,k(n-1)}};
(3)按照如式(1)计算当前向量xk(n-1)对set集合中的剩余列向量xj投影
j∈set
(1)
(4)获取最大投影值Pxj所对应的波长k(n),则k(n)=arg(max(‖pxj‖)),j∈set;
(5)将最大投影值Pxj作为下次迭代时的初始值,即:xj=Pxj,j∈set;
(6)令n=n+1,若n (7)直到n=N,循环结束,最终提取出的特征波长位置为{k(n),n=0,1,…,N-1}。 对应于每一个初始k(0)和N,在循环一次后计算出交叉验证集对应的均方根误差,其中均方根误差最小值所对应的k(n)即为筛选出的特征变量组合。本文应用SPA算法从原始荧光光谱中筛选出与样本浓度关系最为显著的少数几个波长点作为特征光谱,基于特征光谱回归建模能够减少计算量,进一步提高模型的训练速度。 最小二乘支持向量机方法将传统支持向量机(Support vector machine,SVM)的不等式约束转变为等式约束,将SVM所对应的二次规划问题转换成了线性方程组的求解[21,22],其简化了计算且训练速度明显快于传统支持向量机方法。 LSSVM用于回归时,其损失函数定义为误差的二次项,对应如下优化问题 s.t.:yk=wTφ(xk)+b+ekk=1,…,N (2) 式中:误差e类似于SVM问题中的松弛变量,参数γ与惩罚变量的意义相同,作为权重用于平衡寻找最优超平面和偏差量最小这两个因素。 应用拉格朗日方法求解上述优化问题可得 b+ek-yk} (3) 式中:αk,k=1,…,N,为拉格朗日乘子。根据优化条件,分别对w、b、ek、αk求导,即 (4) 可得: αk=γek wTφ(xk)+b+ek-yk=0k=1,…,N (5) 将其转化为如下线性方程组的求解 (6) 式中:核矩阵Ωkl=φ(xk)Tφ(xl)=K(xk,xl),k,l=1,…,N。 求解上述方程组可得LSSVM的回归函数为 (7) 本文提出了将连续投影算法与最小二乘支持向量机方法相结合,用于对混合农药残留的定量分析。实现流程如图1所示。 图1 SPA-LSSVM算法流程 对应的算法步骤为: (1)获取样品光谱信息,将原始光谱属性矩阵记为XM×J(M为样本数,J为波长个数); (2)应用连续投影算法,从XM×J对应的全波长中优选出特征波长点,记为Kn(1≤n≤N); (3)将Kn对应的特征光谱属性矩阵XM×N作为最小二乘支持向量机的模型输入,样品浓度作为模型输出,训练回归模型; (4)训练完成后即可获得LSSVM回归函数,用于对未知样品的含量预测。 分别配制浓度均为0.1 mg/mL的灭蝇胺、异丙甲草胺、克菌丹、噻虫嗪标准溶液各100 mL,放置备用。从标准溶液中量取不同的4种农药进行混合并摇匀,共配制完成156个四组分混合农药测试样本,应用LS55荧光光度计检测每个混合溶液的荧光光谱,设置仪器采样间隔为0.5 nm,波长范围为300~500 nm,激发波长为280 nm,狭缝宽度为6.0 nm。 试验样本共156个,每个样本的荧光光谱中共有401个波长,波长范围为300~500 nm,波长间隔为0.5 nm。4组分混合农药样本的荧光光谱如图2(b)所示。图2(a)为4种农药各自对应的荧光光谱,其中,异丙甲草胺的荧光峰位于334 nm,灭蝇胺、克菌丹两者的荧光峰均为340 nm,噻虫嗪对应的荧光峰在350 nm处,由此可见各组分之间有较严重的光谱重叠。 图2 农药荧光光谱 将混合农药荧光光谱对应的属性矩阵记作X(156,401),则156代表样本个数,401代表300~500 nm光谱范围内的采样点个数。样本浓度矩阵可记作y(156,4),共4列,分别对应4种农药的浓度。从试验样本中随机抽取102组作为训练集,剩余54组作为测试集。将数据集导入MATLAB平台后,基于LSSVM方法建立四组分混合农药的回归模型并测试验证。 SPA-LSSVM模型的建立过程如图3所示。获得四组分混合农药的荧光光谱后,首先,对光谱进行平滑、归一化预处理,分别以每种农药的浓度为因变量,混合农药样本对应的荧光强度为自变量,应用SPA算法优选出每种农药对应的特征波长,共获得4组不同的特征波长组合,每组特征波长表示其位置处的荧光强度对该种农药的浓度变化最为显著,为了获得较全面的荧光属性且不漏掉较显著的荧光波长,对四组特征波长取其合集作为该混合农药所对应的特征波长点;然后,应用LSSVM方法进行模型训练,其中模型输入为特征波长处的荧光强度,模型输出对应4种组分的浓度值;最后,对模型预测性能进行测试,并与传统PLS方法分析对比。 图3 SPA-LSSVM模型建立过程 模型评价主要通过决定系数(相关系数的平方,R2)、校正均方根误差(Root mean square error for calibration,RMSEC)、预测均方根误差(Root mean square error for prediction,RMSEP)等参数对本文的SPA-LSSVM方法及传统PLS方法性能进行对比,决定系数、均方根误差的计算式如下 (8) 以混合农药对应的401个波长处荧光强度为自变量,以每种农药的浓度为因变量,应用SPA算法分别优选出4种农药对应的特征波长点,算法中的特征维数范围设置为:1~20,其筛选出的特征波长结果如图4所示。其中,灭蝇胺对应11个特征波长点,说明这11个波长处的荧光强度对灭蝇胺浓度变化较为显著。异丙甲草胺、克菌丹、噻虫嗪对应的特征波长个数分别为:11、8和14。由图4可知,4种农药优选出的特征波长个数虽然不一致,但其大部分重合或者非常接近,本文将4种结果求合集作为最终的SPA特征波长优选结果,共获得25个特征波长,其分布如图5所示。 图4 4种农药对应的SPA特征波长分布 图5 混合农药残留SPA特征波长分布图 由图5可知,合集中的25个特征波长点分布于300~500 nm的整个区间,在特征峰340 nm处比较集中。尤其在光谱趋势发生显著变化的位置,均对应特征波长点。 以SPA算法所优选出25个特征波长处的混合农药荧光强度作为输入,应用LSSVM方法训练多回归模型。模型参数设置如下:核函数选用径向基核函数(Radial basis function,RBF),其表达式为K(xi,xj)=exp(-g‖xi-xj‖2),参数g的取值大小影响模型的分类精度;以网格搜索法优化LSSVM参数,即分别针对惩罚因子和核函数参数设定搜索范围,在指定区间内实现参数的寻优;另外,设置5折交叉验证。模型训练完成后分别对训练集、测试集进行测试验证,结果如图6和图7所示。 由图6可知,训练集的模型测试结果较为理想,除了噻虫嗪对应的决定系数稍低,其他3种农药对应的决定系数均大于0.9。图7中的测试集验证结果整体低于训练集,异丙甲草胺中有个别样本点对应的测试误差较大,其他3种农药对应的模型决定系数均大于0.8。 为验证SPA-LSSVM方法的优越性,应用传统PLS方法对该四组分混合农药进行回归分析,针对训练集、测试集分别进行测试验证,结果如图8和图9所示。 由图8和图9可知,PLS方法对应的训练集预测精度稍优于测试集。以灭蝇胺农药为例,其训练集对应的均方根误差(RMSEC)为0.003 6 mg/mL,优于测试集的均方根误差(RMSEP)0.005 5 mg/mL;训练集对应的决定系数为0.939 2,也优于测试集对应的0.912 8。其余3种农药,均表现出类似的性能测试结果。 图6 训练集SPA-LSSVM回归结果 图7 测试集SPA-LSSVM回归结果 图8 训练集PLS回归结果 图9 测试集PLS回归结果 为了验证SPA-LSSVM方法性能的优越性,在同等试验条件下,基于全波长对该混合农药进行了支持向量机方法的回归分析,分别将SPA-LSSVM、SVR、PLS 3种模型结果列于表1中。 由表1可知,针对训练集,SPA-LSSVM对应的4种农药校正均方根误差RMSE均低于PLS方法,且其决定系数R2均高于PLS;将其与SVR模型结果进行对比,发现除了噻虫嗪之外,其他3种农药的含量预测结果均显示SPA-LSSVM方法的性能更优。对测试集来说,前两种农药(灭蝇胺、异丙甲草胺)对应的SPA-LSSVM性能参数稍低于PLS方法,而后两种农药(克菌丹、噻虫嗪)则是SPA-LSSVM方法所对应的预测精度更高,再将其与SVR模型结果进行对比,发现除了编号为2的农药(异丙甲草胺)对应的预测结果相接近,其余3种农药均显示SPA-LSSVM具有更优的预测性能。 为了更加显著地对比SPA-LSSVM、SVR、PLS方法的预测性能,将各项模型参数曲线绘制于图10中。 显然,综合训练集、测试集两者的测试结果可知,SPA-LSSVM方法的预测性能更优。可见SPA方法能够有效优选出混合农药荧光光谱中的特征波长点,且这些波长处对应的荧光强度与各成分的浓度之间具有较显著的关系,故基于这些特征波长点训练完成的LSSVM模型更具优越性。另外,相比传统PLS方法以及基于全波长的SVR方法,SPA-LSSVM不仅预测性能更优,且其因为只有25个特征波长作为输入,使得对应的模型形式更加简单,且训练速度大大加快。 表1 SPA-LSSVM、SVR、PLS方法性能参数 图10 SPA-LSSVM、SVR、PLS方法性能参数对比 本文提出一种基于SPA-LSSVM的多组分混合农药残留荧光检测分析方法。这种方法首先应用SPA算法优选出特征波长,有效消除了荧光光谱间的相关性,然后基于LSSVM方法训练定量分析模型,并分别对训练集、测试集进行模型测试,结果表明这种方法的预测性能优于传统PLS方法。这说明连续投影算法方法能够有效筛选出混合农药的特征荧光光谱,且应用最小二乘支持向量机模型对其中的多组分进行定量分析时,具有较高的预测精度。本文对SPA-LSSVM方法的有效性进行了分析验证。1.2 最小二乘支持向量机
1.3 SPA-LSSVM算法流程
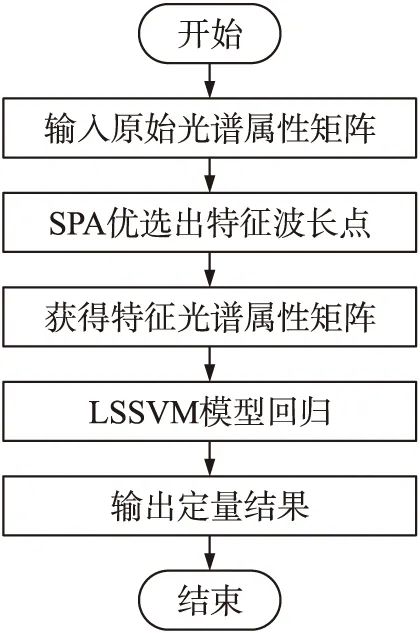
2 试验与分析
2.1 检测过程
2.2 样本数据集

2.3 SPA-LSSVM模型建立过程

2.4 模型性能评价

3 结果与讨论
3.1 SPA优选特征波长


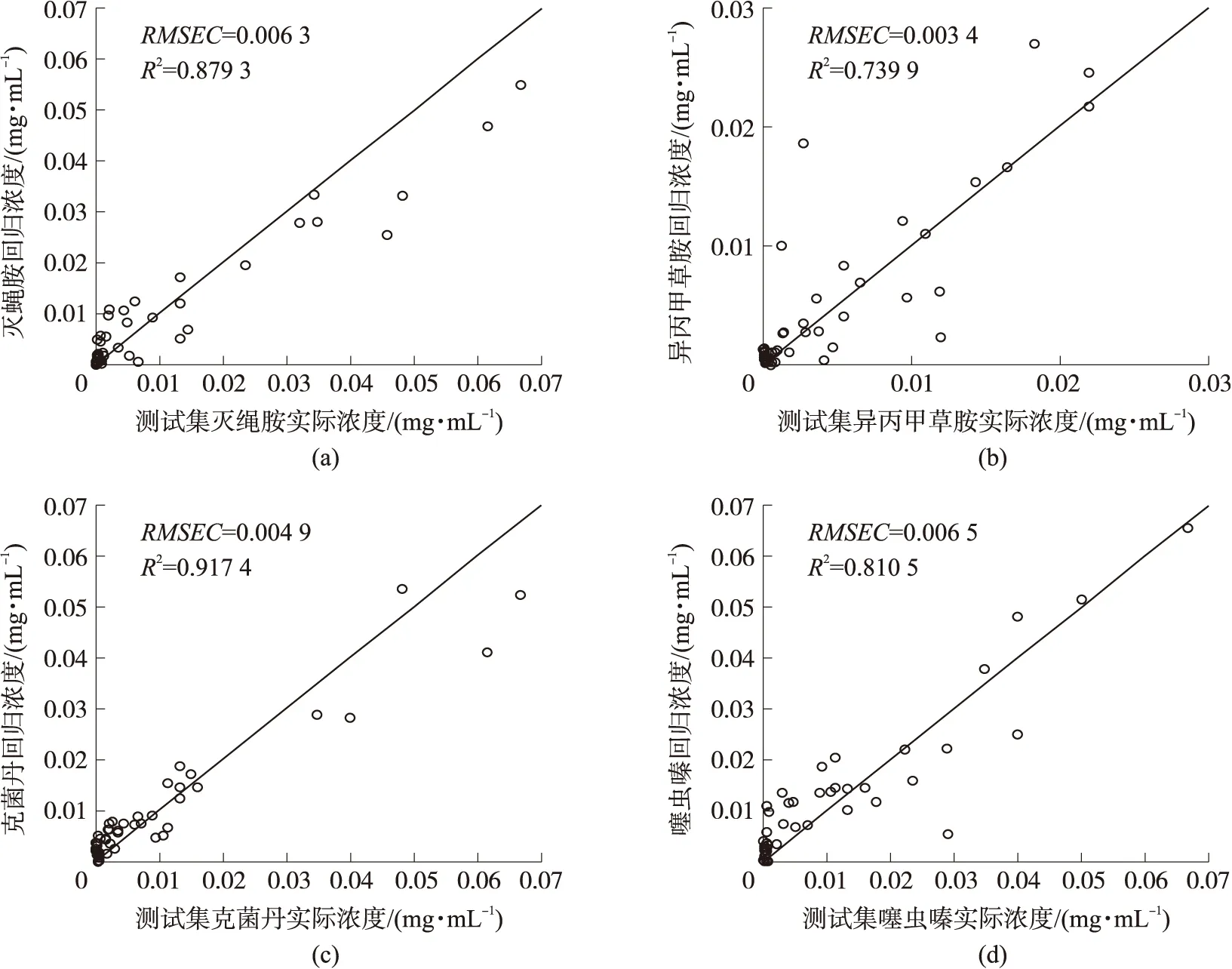
3.2 LSSVM模型结果
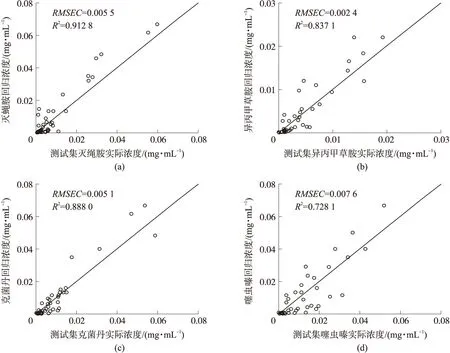
3.3 传统PLS模型结果


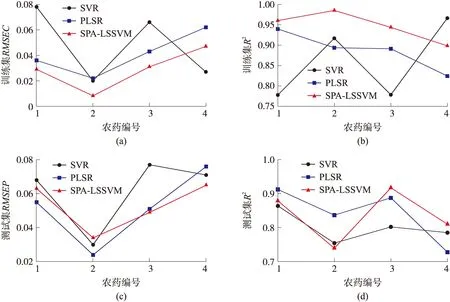
3.4 SPA-LSSVM与PLS、SVR方法的性能对比

4 结论

