基于分通道自适应理论的阈值分割算法及评价
李 洁,于艺铭,陈 茜,王小菊,王 琪
(南京林业大学 轻工与食品学院,江苏 南京 210037)
图像分割是指按照一定规则将源图像中感兴趣目标区域与其背景进行分离的技术[1]。随着计算机视觉和计算机图形学的发展,图像分割技术已成为图像处理的关键环节之一,是图像分类、场景解析、物体检测、图像3D重构[2-5]等任务的预处理步骤,被广泛应用于工业检测、环境监测、军事和宇宙探索等多个领域[6]。最早出现的分割算法为阈值法[7],随着分割场景的复杂化,陆续出现了边缘检测法[8]、区域提取法[9]、聚类分析法[10]和特定理论等的分割方法。阈值法因其实现简单且性能较为稳定[11]而成为图像处理中最广泛使用的分割技术。其中,最佳阈值的选择在该分割法中尤为重要,已经有许多学者针对这一点做出了不同程度的研究和改进。Liao等[12]修改了类间方差的计算公式,通过优化筛选规则大大缩短了算法整体运行时间。李敏等[13]将均方差因素引入传统分割方法,将最大类间方差法进行改进,主要运用于纹理较为复杂的脑部切片图像分割;王鑫等[14]基于数学形态学运算,运用分水岭分割法较好地解决了在边界不明显的细胞图像分割中出现的过分割及欠分割问题;裴继红等[15]提出了多阈值分割法,通过对直方图模糊约束目标函数的优化获得最佳模糊约束划分,根据最大隶属度原则进行图像多阈值化分割,对文本类图像有较好的分割效果。Ahmed等[16]提出应用于磁共振成像数据模糊分割的纠偏模糊聚类(Bias-Corrected fuzzy C-means,BCFCM)算法,将像素周围空间信息加入到原始模糊聚类(Fuzzy C-means,FCM)算法中,提高了分割结果精度。童何俊等[17]提出一种光学相干断层图像的边缘检测法,利用自主生成的结构元素对边界不鲜明的光学相干断层扫描(Optical coherence tomography,OCT)图像进行形态学边缘检测滤波,实现了对目标边界的提取。田文启等[18]在色调饱和值(Hue saturation value,HSV)色彩空间采用最大类间方差法OTSU分割算法将图像分区,并对逆光区进行自适应对数变换,在逆光图像的分割中具有较好的适用性;吕鑫等[19]在改进麻雀搜索算法的基础上,提高了多阈值图像分割算法的性能,对部分图像的分割速度和精度都得到了提升;张田等[20]以图像清晰度评价函数度量图像阈值化后内灰度的相似性,改进了自适应阈值图像分割法,提高了低对比度图像的分割精度;王卓等[21]对图像噪声进行灰度压缩细分边缘像素,引入动态参数增强算法的自适应性,提高了背景较为单一图像的分割精度。已有研究成果对具有明显特征的某一类图像进行算法选择与改进后,提升了分割效果,但算法的应用范围较窄,仅对某一类图像具有适用性。
为了进一步提高分割算法的普遍适用性,实现对多种色貌类型及纹理特征图像的精准分割,本研究提出了一种在Lab颜色空间下的基于分通道自适应理论(Adaptive theory of sub channels,ATSC)阈值分割算法。将这算法应用到多类型图像的分割中,均可获得较好的分割结果,拓宽了阈值分割法的适用范围,提高了图像分割的精度。可为医学影像处理、生物特征识别、色彩迁移、图像修复等多种领域提供精准可靠的图像特征信息,解决传统分割算法图像适用性单一的问题。
1 算法原理
1.1 算法描述
该算法的流程图如图1所示。
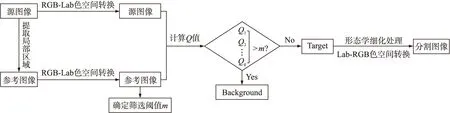
图1 本文分割算法流程图
为了提高阈值分割法的适用性,本文将Welsh算法中的自适应理论[22-24]引入到图像分割中。由于红绿蓝(red,green,blue,RGB)颜色空间各分量间相关性较大,一个分量值的改变必将引起其他分量值发生变化,而Lab三通道间具有序列不相关性[25],消除了单一目标区域受多通道交互影响的弊端,因此Lab空间为本文所选择的颜色空间。首先在源图像中提取待分割目标中具有代表性的局部区域为参考图像,如图2所示;然后将两幅图像分别从RGB颜色空间转到Lab颜色空间进行计算分析;其次,观察图像特征,选择合适的通道,将参考图像在该通道下的极差值和方差值进行加权运算,得出最佳阈值m;综合考虑像元的灰度值、8-邻域均值和8-邻域标准差来计算源图像与参考图像像元之间的匹配误差Q,根据m和Q值的大小关系,将源图像中每个像元划分到目标与背景两个区域;最后将图像经形态学细化处理并转回RGB颜色空间,得到分割后的图像。
1.2 确定筛选阈值m
本文分割算法首先提取源图像中目标对象的局部区域作为分割模型的参考图像,如图2所示,蝴蝶为目标区域,树叶为背景区域,相较于蝴蝶的黑色身体部分,蝴蝶翅膀上的颜色以及特殊纹理更能代表蝴蝶的整体特征,故提取蝴蝶翅膀上具有代表性的部分区域为参考图像。参考图像中的像素值可为筛选阈值m的计算提供依据,极大地缩短计算时间。

图2 参考样本提取
通过makecform、applycform函数将导入的待分割源图像及提取的参考样本由强相关性的标准红蓝绿(Standard red green blue,SRGB)模式转换为序列不相关性的Lab模式。为确定最佳筛选阈值,本研究综合考虑参考图像的内部交互关系,找出参考图像区域与背景区域像元属性差异最大的通道T(L通道、a通道、b通道),在这通道下选用参考图像的“标准差”与“极差”的加权结果作为本文分割模型的筛选阈值m,如式(1)所示
m=a1(Tmax-Tmin)+a2σT
(1)
式中:Tmax、Tmin分别为参考图像T属性通道的最大与最小值;σT为参考图像T属性通道的标准差;a1、a2分别为上述“极差”与“标准差”所占权值,a1、a2∈[0,1]且a1+a2=1。
最优加权系数的选定规则因图而异,当参考图像内部像元间T属性通道值差别总体较大时,“标准差”权值a2应高于“极差”权值a1;反之,“极差”权值a1应高于“标准差”权值a2。
1.3 确定匹配误差Q值
Welsh自适应理论起源于2002年提出的一种经典灰度图像彩色化算法,算法核心思路是以空间中某像元邻域灰度信息最相近原则为筛选条件,从参考图像中自适应检索与源图像的最佳匹配像元,在保留源图像亮度信息的前提下,将参考图像像素的颜色信息迁移给源图像中的对应像素。模型中自适应思想体现如下
G(p1,p2)=arg min[S(p1)-R(p2)]2
(2)
式中:p1、p2分别为源图像、参考图像像素;S(p1)、R(p2)分别为两类像素的邻域灰度值;G(p1,p2)为源图像、参考图像的最佳像元组合。
由式(2)可知,该理论通过邻域灰度值最相近原则,找到当前像素与参考区域所有像素中相似性距离最小的点,实现二者的最佳匹配效果。
本文不仅将上述Welsh自适应理论运用到彩色图像分割中,而且对其匹配误差的计算公式进行改进。为保证模型分割结果的精确度,在计算源图像与参考图像匹配误差时,综合考虑了源图像与参考图像各像元的8-邻域特性。如式(3)~(5)所示
Q=a3|Ti-Tj|+a4|μi-μj|+a5|σi-σj|
(3)
(4)
(5)
式中:Ti、Tj分别为源图像与参考图像逐像素的T通道值;μi、μj、σi、σj分别为二者逐像素的T通道8-邻域均值与8-邻域标准差。对于待分割源图像中的每个像素i,依次计算其与参考图像中所有像素j的Q值,记为Qg,并与1.2节中确定的最佳筛选阈值m进行比较,分配结果如式(6)所示
(6)
由式(6)可知,若源图像中像素i与参考图像中所有像素j的匹配误差Q值均大于最佳筛选阈值m,则将像素i归为背景区域;反之,将像素i归为目标区域。循环算法(3)~(6),直至完成源图像中所有像元的分配,实现目标区域的分割。
1.4 形态学细化处理
为达到更精确的分割效果,本文运用腐蚀、膨胀等形态学运算对自适应分割后的结果图像进行细化处理,以消除目标区域边界处多余像元。如式(7)、(8)所示
A⊗B={x,y|Bxy⊆A}
(7)
A⊕B={x,y|Bxy∩A≠∅}
(8)
如图3所示,经过形态学细化处理,可以将边缘进行细化,删除多余像元,同时获取蝴蝶更完整、更丰富的形态细节。

图3 形态学细化处理
2 本文算法试验结果
本文在Matlab编译环境下实现算法,为检验图像分割效果,试验展示了10组采用本文分割方法所得的目标与背景彩色分割图,为更直观地判断图像边缘的分割效果,同时展示其二值效果图作为评价依据,如图4所示。10组图像中包括了人物、动物、自然风景、人文建筑、金属器皿和植物果蔬等图像常见元素,具有充分的代表性。

图4 基于分通道自适应理论的阈值分割算法试验图像
图4中,(a)为上述10组不同类型图像的待分割源图像,(b)、(c)、(d)分别为目标提取结果、背景提取结果及二值图像。可以看到,使用本文算法可以较好地将这10组不同类型图像的目标与背景区域分离,观察第3组与第5组的二值图像可以看出其边缘处分割较为精细,且均未出现明显的过分割或欠分割现象。表明本文算法不仅有优秀的分割效果,而且有较好的图像适用性。
3 算法评价
3.1 不同算法的分割效果
对本文ATSC算法的分割效果进行评价,并与多阈值分割法(Multi-thresholding segmentation,MTS)、光学相干边缘检测法(Optical coherent edge detection,OCED)、模糊C均值聚类算法(Fuzzy C-means algorithm,FCM)、极值分析法(Extreme value analysis,EVA)、最大类间方差法(OTSU)、分水岭分割法(Watershed algorithm,WA)、和K均值聚类分割法(K-means clustering algorithm,K-means)共7种常用算法的分割效果进行比较。如图5、图6所示,图5为10组图像分别运用8种算法分割的效果图,图6为其对应的二值图像。

图5 经典分割法及本文分割法的目标结果

图6 经典分割法及本文分割法的二值结果
由图5、图6可以看出,ATSC对于10组图像均有较好的分割效果。OCED和K-means对大部分图像都能较准确地分割,但在第1组和第2组的分割结果中出现了较明显的过分割和欠分割现象,且在3~5组图像中的轮廓细节处理中稍有欠缺。而MTS和OTSU在10组图像中均未取得较满意的分割结果。本文ATSC分割算法能在较复杂的色貌和纹理环境中准确识别目标与背景区域,在保留轮廓信息完整性的同时,对内部及边缘的细节处理也较好。表明本文算法的分割性能优于其余7种传统算法,并且具有一定的适用性。
3.2 分割算法评价
本文采用均匀性测度(Uniformity of intraregion,RU)、准确率(Precision,PRE)、召回率(Recall,REC)与轮廓精度(Boundary F-measure,FME)共4个评价指标对ATSC及7种常用的分割算法进行评价与比较。
3.2.1 区域内均匀性测度评价
采用RU表示不同源图像中已分割区域内部均匀性测度指标,对使用以上8种分割方法所得的目标结果图进行定量评价。
(9)
式中:Ri表示第i个分割区域;Ai表示其面积;C为归一化因子;f(x,y)为通道值;n为第i个区域内的像素数。RU值越大越接近于1表明分割效果越好,表示该算法性能越好,如表1所示。

表1 不同图像的RU评价
由表1可知,对于10幅不同类型图像的目标区域分割结果图,本文ATSC分割算法的RU值均大于其他分割算法的RU值,且都大于0.95,表明已分割区域内部的特征点分布较均匀,分割效果较好,与试验结果所示一致。
3.2.2 准确率、召回率与轮廓精度评价
采用PRE、REC和FME对本文图像分割算法的目标区域分割效果图进行评价,模型如式(10)~(12)所示
(10)
(11)
(12)
式中:目标对象正确分割为目标区域的像素点的个数记为TP;背景错误分割到目标区域的像素点的个数记为FP;目标对象错误分割到背景部分的像素点的个数记为FN。FME是对分割结果全面、综合的评价。PRE、REC和FME的数值越大越接近于100%,则该算法的分割效果越好,如表2所示。
由表2可知,本文分割算法的PRE、REC和FME值均大于其余7种分割算法的值,且都接近于100%,表明本文分割算法的分割精度、准确率都较好,且算法整体性能较好,有较好的图像适用性。

表2 不同图像的PRE、REC、FME评价
3.2.3 数据可视化分析
如图7所示,为更直观立体地展示以上4个评价指标对7种经典分割模型与本文模型共8种分割方法的综合评价结果,构建4个立体直方图进行综合分析。其中x轴为1~10组试验图像,y轴为上述1~8种分割模型,z轴为上述评价指标的数值结果。由上述可视化数据结果和试验所得的分割图像进行综合分析,本文ATSC分割模型所得目标图像的RU、PRE、REC与FME值均高于其他7种经典分割模型,与试验所得的分割图像结果一致。表明ATSC的分割性能优于其余7种算法,改善了其余几种算法在处理图像时出现的边缘误判、内部信息丢失等问题,尤其是纹理属性较为显著或色貌环境复杂的图像,验证了这算法具有较好的分割性能且具有较好的适用性。

图7 综合评价指标
4 结论
本文针对几类经典模型存在的分割精度不足且适用性稍有欠缺的问题进行改进,利用Lab色模型的序列不相关性理论为试验基础,将Welsh算法中的自适应理论运用到图像分割中并对其进行改进,即提取源图像中具有代表性的目标区域为参考图像,并将两幅图像从RGB颜色空间转到Lab颜色空间;以参考图像的信息确定筛选阈值m;综合考虑像元的灰度值、8-邻域均值和8-邻域标准差计算得出匹配误差Q值;将源图像中所有像素点分为目标与背景两部分,对分割结果进行形态学细化处理,再将图像从Lab空间转到RGB颜色空间得到最终结果,实现了对不同色貌图像的准确分割。采用RU、PRE、REC和FME 4种评价模型分别对8种分割算法的处理效果进行评价。试验及评价结果中,本文算法评价所得RU值均大于0.95,PRE值均大于98%,REC和FME的值均大于98.5%。表明本文算法可较好实现各类复杂图像中目标与背景的提取,算法具有较强的适用性,有效减少了传统分割方法中出现的欠分割以及过分割等现象,所得分割图像的内部均匀性和分割精确性等方面都优于传统分割算法。

