利用背散射伽马射线确定套管厚度的模拟研究

邱 飞,张 锋,2,张 慧,钟路予,鲁保平

(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071;3.中国石油集团测井有限公司,陕西西安 133200)

套管是油气勘探中连接地下与地面的重要通道,在油气井施工及生产中发挥着关键作用[1-2]。复杂的地质运动、地下环境及不当的人为施工是造成套管损伤的主要原因[3-4]。套管缺损所导致油水层窜槽等事故成为制约石油开采的瓶颈,有效的套管检测技术对油气田可持续生产和安全问题具有重要意义[5]。常见的套损检测测井方法有井壁超声成像测井[6]、多臂井径测井及电磁探伤测井[7],其中多臂井径测井采用井径臂与套管内壁接触测量方式直接确定套管内径,测量灵敏度高;井壁超声成像测井采用旋转扫描的方式检测套管内径和厚度,周向分辨率高;电磁探伤测井利用在套管内产生的涡流判断管柱裂缝,利用感应电动势随时间衰减速度计算套管厚度,可以评价多层管柱状况。基于伽马射线散射原理的厚度测量及损伤探测已在地面和井下得到广泛应用。多名学者通过研究多次散射衰减及背散射伽马射线强度与介质的作用过程,建立了利用射线强度来评估介质厚度及密度的测量方法[8-9]。Margret等[10]将Cs-137源与探测器放在同一侧,通过记录背散射伽马射线在地面进行钢材探伤;Sharma等[11]、廖常庚等[12]利用准直后的伽马射线照射油管,根据散射伽马射线强度探测油管完整性;Park等[13]综合利用X射线的荧光性和康普顿散射评价有机物厚度,根据有机物的厚度选择灵敏度高的评价参数。针对井下套损评估,俄罗斯cгд测井仪利用Cs-137源和一个近探测器(源距21 cm),通过接收高能伽马射线,利用经验公式获取套管厚度[14-15];李晓龙等[16]基于三探测器岩性密度仪器,利用高能伽马射线计数率反演得到套管厚度。上述方法均采用正源距探头通过记录单一能窗计数评价套管厚度,测量结果受仪器工作状态影响较大,同时地层和水泥环参数也会直接影响套管厚度计算结果。笔者基于伽马射线在介质中的散射和衰减理论,根据套管光电吸收截面和康普顿散射截面均高于常规地层和水泥环介质的特点,提出利用康普顿背散射窗和光电窗的双能窗组合法评价套管厚度,通过蒙特卡罗方法建立不同套管厚度条件的正演计算模型,对比研究不同窗计数组合方法的灵敏度,建立计数比与套管厚度的响应关系;模拟研究不同水泥环、地层参数对确定套管厚度的影响;最后通过模拟实例进一步验证该方法的可行性。

1 散射伽马射线测厚原理

Cs-137伽马源放出0.662 MeV的单能伽马射线进入由套管、水泥环和地层组成的介质后,作用过程主要包括光电吸收和康普顿散射。当探测器源距足够小时,其所接收的伽马射线主要为背散射伽马射线,即与介质发生散射角度接近180°的一次散射作用,伽马射线强度主要取决于以下因素:源强、介质的衰减系数和衰减长度、介质的电子数和散射截面、散射立体角[10],即

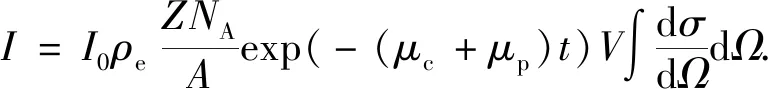
(1)

式中,I0为初始源强;μc和μp分别为介质的康普顿线性系数和光电吸收系数;t为伽马射线在介质中的衰减长度;ρe为介质的电子密度;dσ/dΩ为微分散射截面;dΩ为散射立体角;V为介质的散射体积;Z、A和NA分别为介质的原子序数、质量分数和阿伏伽德罗常数。式(1)中微分散射截面在仪器结构固定的条件下为常数,可以看出伽马射线强度主要与介质的密度、尺寸以及衰减系数有关。图1给出了套管井内井周主要介质井眼流体(H2O)、套管(Fe)、水泥环(CaSiO3)和地层(CaCO3、SiO2)的光电线性吸收指数与康普顿线性系数(20%CaCO3和20%SiO2分别代表孔隙度20%的含水灰岩和砂岩地层)。

根据不同介质光电吸收系数和康普顿衰减系数与射线能量的关系可以看出:套管的光电吸收系数和康普顿衰减系数远大于常见地层和井眼介质,表明套管是引起伽马射线强度变化的主要介质;当伽马射线能量为0～0.12 MeV时,其与套管同时发生光电作用和康普顿散射,由于光电截面远大于康普顿截面造成该能量范围内伽马计数主要由光电效应产生,由于套管厚度通常小于1 cm,因此将伽马射线在套管中的衰减路径近似为套管厚度,低能部分伽马计数I1可表示为

I1=I0exp(-(μc(E′)+μp(E′))t).

(2)

式中,μc(E′)和μp(E′)分别代表能量为E′时套管的康普顿线性系数和光电吸收系数,可以看出低能伽马计数随着套管厚度的增加而降低。

当伽马射线能量高于0.12 MeV时,康普顿线性系数逐渐高于光电吸收系数,并且光电吸收系数随着能量的增加进一步降低,因此能谱中的高能部分计数I2主要反映康普顿散射作用,其计数可以表示[13]为

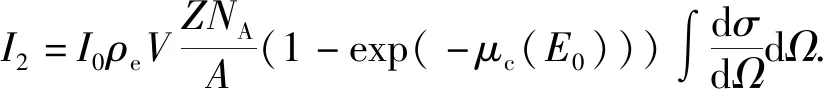
(3)

式中,E0为伽马射线的初始能量。高能伽马射线主要与介质发生背散射,伽马计数随着套管厚度的增加而增加。

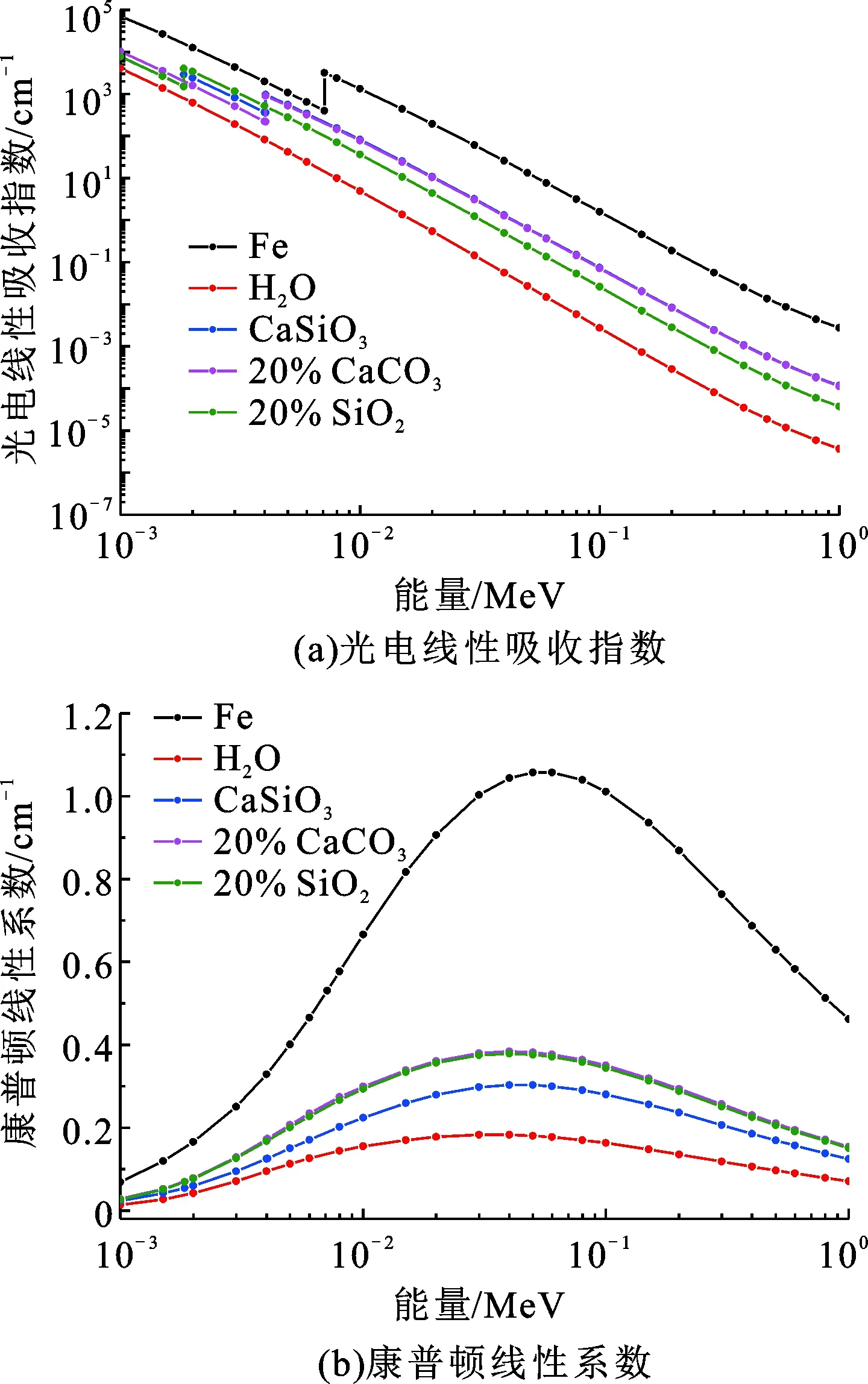
图1 不同介质伽马散射截面与能量的关系Fig.1 Gammaray scattering cross section versus energy for different media

利用高能和低能计数比消除源强影响,得

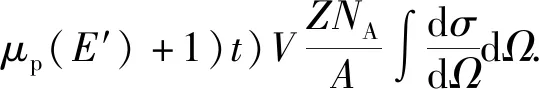
(4)

基于上述分析,当套管厚度增加时,高能计数I2增加,而低能计数I1降低,两者相反的计数变化规律理论上会提高套管厚度确定的灵敏度。

2 数值模拟

蒙特卡罗数值计算方法广泛应用于核测井仪器参数优化、测井响应及数据处理方法[17-18]。为研究背散射伽马射线与套管厚度的响应关系,利用蒙特卡罗方法建立数值计算模型,研究伽马计数、计数比响应规律及影响因素,建立套管厚度评价方法。

2.1 计算模型

建立如图2所示的蒙特卡罗计算模型,其中地层半径为50 cm,套管内径为80 mm且井眼内充满淡水,套管厚度为7 mm,密度为7.8 g/cm3;水泥环厚度为3 cm,密度为1.95 g/cm3;地层为孔隙度10%的石灰岩地层,密度为2.54 g/cm3。测量仪器由一个Cs-137伽马源和一个NaI伽马探测器构成,仪器直径为60 mm,NaI晶体直径和长度分别为1和1.5 cm,仪器外壳材料为钢,密度为7.78 g/cm3;考虑到背散射伽马射线探测和实际仪器结构的需要,探测器源距为6 cm,伽马源与探测器之间放置厚度为3 cm的钨镍铁屏蔽体,密度为18 g/cm3。为使伽马射线定向发射和接收,在伽马源、探测器和仪器外壳之间设置有准直孔,与水平线夹角为45°,设置仪器贴井壁测量。本文中采用蒙特卡罗程序中的F4计数进行伽马能谱探测,计算误差小于1%。

图2 蒙特卡罗计算模型Fig.2 Monte Carlo simulation model

2.2 套管壁厚响应规律

利用图2模型开展模拟计算,地层设为孔隙度10%的含水石灰岩地层,保持水泥环密度和厚度不变,改变套管厚度,分别为0、1、4和7 mm,套管缺损处与水泥环的间隙充填水,模拟得到不同套管厚度下的伽马能谱响应。

如图3所示,不同套管厚度下伽马能谱的能量范围为0～0.5 MeV,根据伽马射线作用过程,按照能量将能谱划分为3部分:能窗Ⅰ(0～0.12 MeV)为光电吸收部分,套管厚度的减小导致套管吸收的光子数目降低,能窗内计数率增加;能窗Ⅱ(0.12～0.23 MeV)为康普顿散射与光电吸收共同作用部分,散射峰约在0.2 MeV附近,计数率随套管厚度的减小而增加表明该能窗内光电作用占据主导;能窗Ⅲ(0.23～0.5 MeV)为康普顿背散射部分,光子发生一次散射后到达探测器,探测器计数与介质的厚度成正比,计数率随着套管厚度的减小而减小。

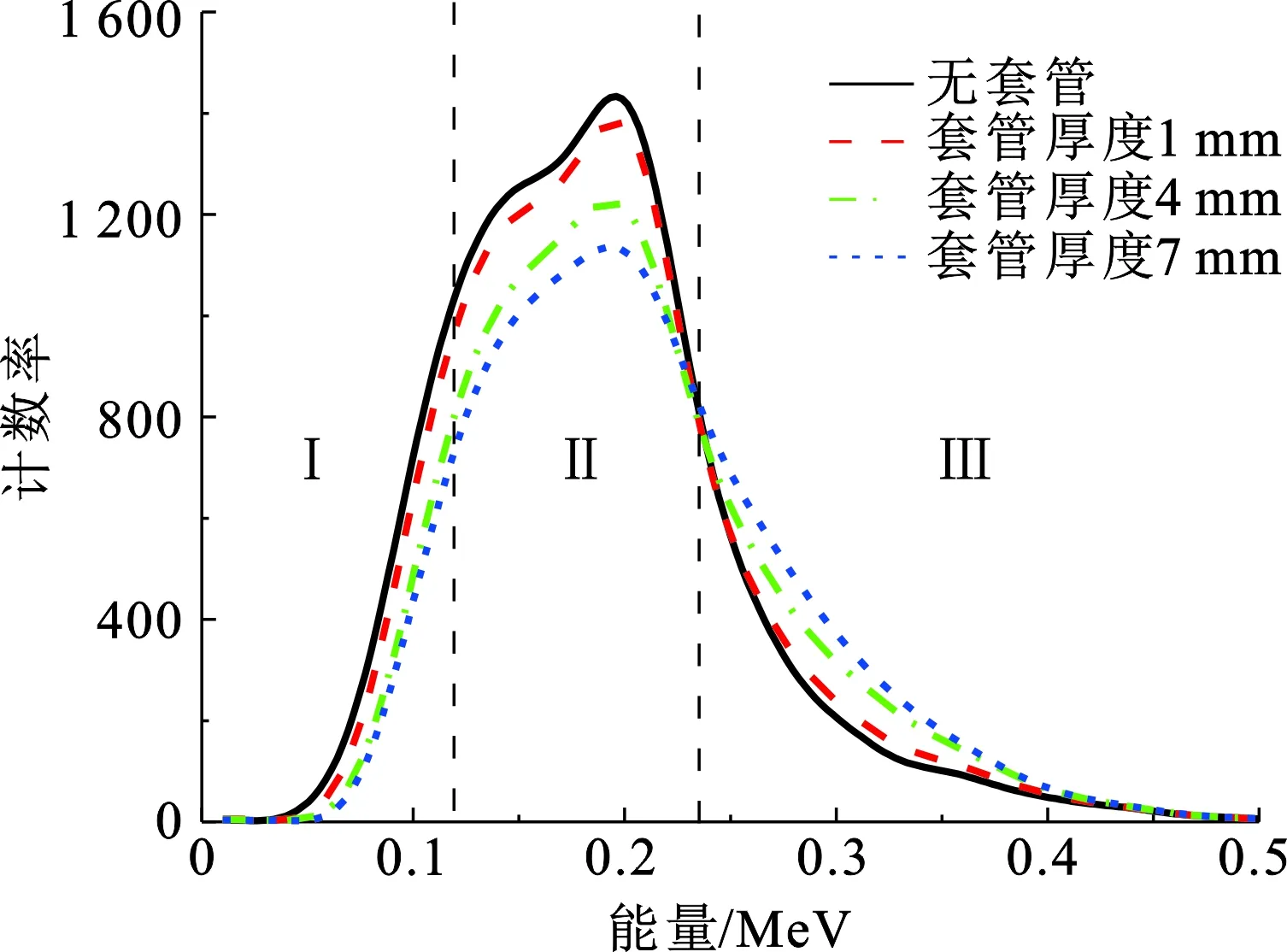
图3 不同套管厚度下伽马能谱响应Fig.3 Gamma ray spectrum response at different casing thickness

图4(a)为能窗Ⅰ、Ⅱ、Ⅲ计数与套管厚度的响应关系,能窗Ⅰ计数由伽马射线与介质的光电吸收作用产生,伽马计数率随着套管厚度的增加而降低;能窗Ⅲ计数主要由伽马射线与介质发生背散射产生,计数率随着介质厚度的增加而增加;能窗Ⅱ中的伽马计数同时由光电效应与康普顿散射,但由于套管的高PE导致光电效应占主导作用,因此计数随着套管厚度的增加而降低。图4(b)为能窗Ⅲ与能窗Ⅰ、能窗Ⅲ与能窗Ⅱ、能窗Ⅲ与能窗Ⅰ、Ⅱ之和的计数比值与套管厚度的响应关系,不同高能与低能窗组合方法的计数比随着套管厚度的增加而增加,为了确定最优能窗组合方法,利用套管厚度变化时计数比的变化率作为相对灵敏度S评价不同计数比组合对套管厚度响应的灵敏程度:

(5)

式中,T为套管厚度;R为计数比。表1为不同能窗组合方法的计数比对套管厚度响应的相对灵敏度(R1为能窗Ⅲ/能窗Ⅰ;R2为能窗Ⅲ/能窗Ⅱ;R3为能窗Ⅲ/能窗Ⅰ+Ⅱ),可以看出能窗Ⅲ与能窗Ⅰ计数比对套管厚度的相对灵敏度最高,尤其在套管厚度较小的条件下优势更加明显。

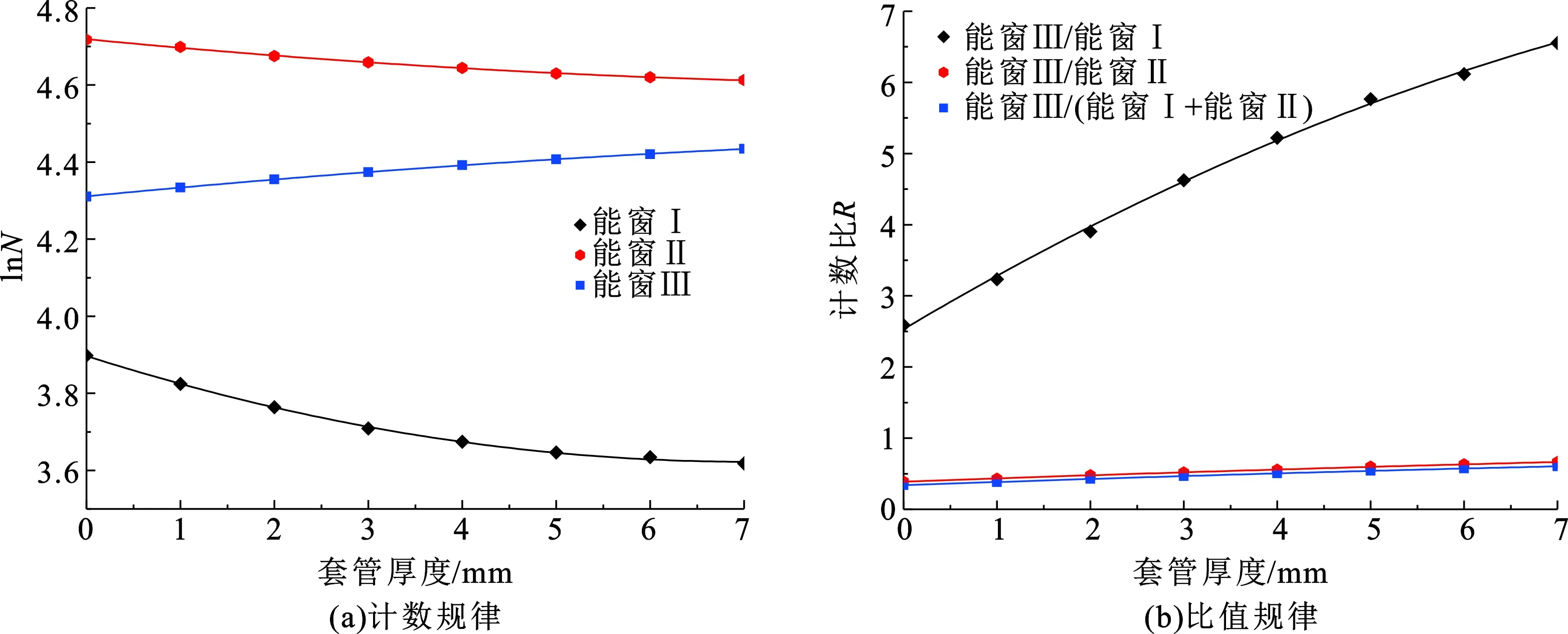
图4 窗计数、计数比与套管厚度响应规律Fig.4 Response law between count rate,count ratio and casing thickness

表1 不同计数比组合下套管厚度响应的相对灵敏度Table 1 Relative sensitivity of casing thickness response for different count ratio combination mm-1

根据图4中能窗Ⅲ与能窗Ⅰ计数比值与套管厚度的响应关系,建立套管厚度评价模型:

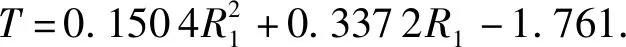
(6)

3 影响因素模拟

由于套管厚度较小,并且在套管周围存在水泥环和地层介质,因此需要确定水泥环与地层参数的变化对评价套管厚度的影响,主要从水泥环厚度、密度和地层密度方面展开研究。

3.1 水泥环厚度

为了研究水泥环厚度对套管厚度评价的影响,设置地层为孔隙度10%的含水石灰岩,水泥环密度保持不变,分别设置水泥环厚度为0、1、2和3 cm,水泥环缺损处填充淡水。在此基础上设置不同的套管厚度,变化范围为0～7 mm,间隔1 mm,模拟得到不同水泥环厚度条件下计数比值与套管厚度的响应规律,如图5所示。

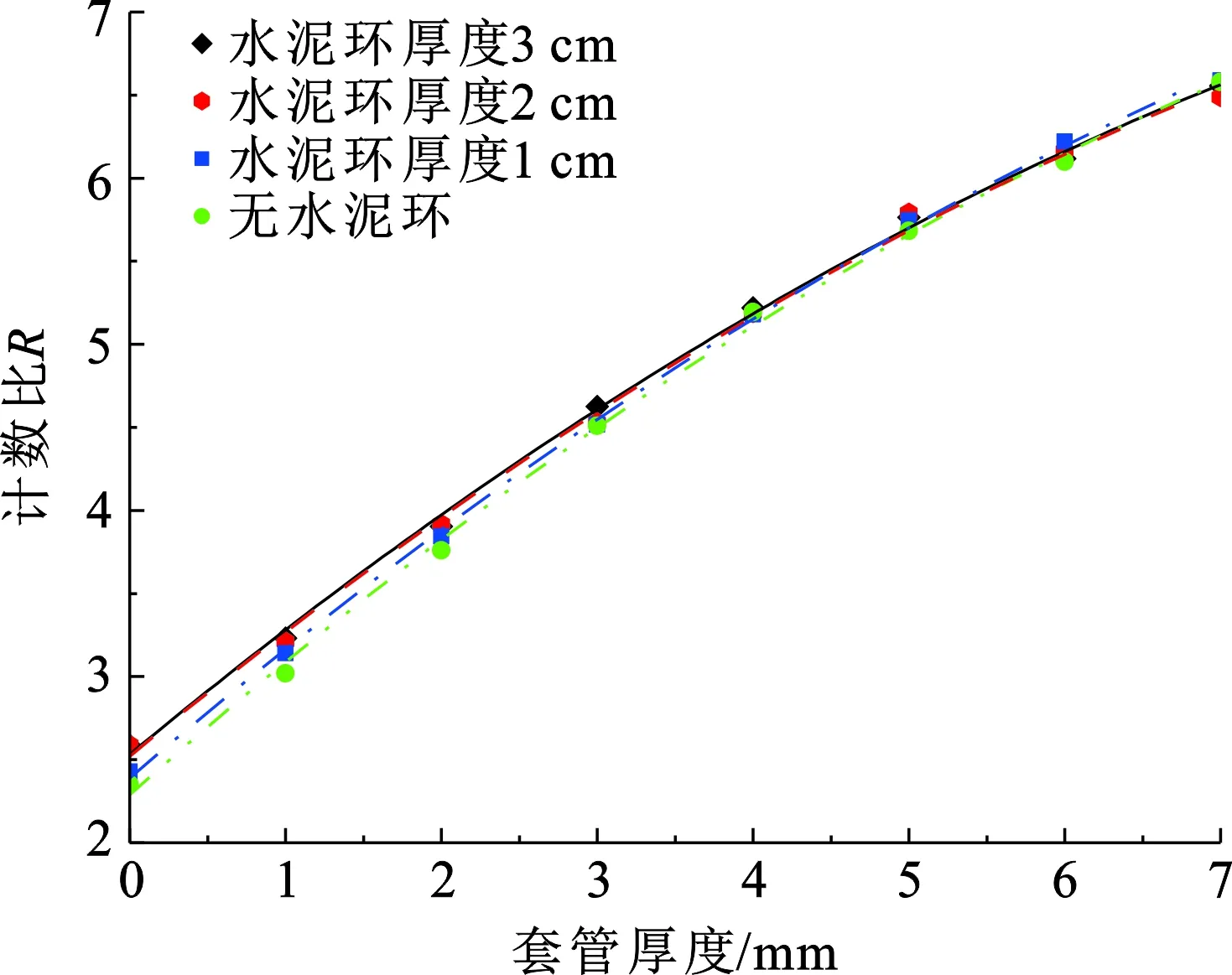
图5 不同水泥环厚度下计数比值与套管厚度的响应规律Fig.5 Response law of count ratio and casing thickness at different cement ring thickness

从图5可以看出当水泥环存在时不同厚度下的计数比值基本一致,当套管厚度小于3 cm且水泥环不存在时计数比略微下降,与3 cm水泥环条件相比其最大变化量为8.7%,出现该现象的原因主要是水泥环的光电吸收截面和康普顿散射截面均远小于套管,套管厚度的变化是造成探测器计数变化的主要因素,因此该方法受水泥环厚度影响较小。

3.2 水泥环密度

为了研究水泥环密度对套管厚度评价的影响,改变地层为孔隙度10%的含水石灰岩,水泥环厚度为3 cm。分别设置水泥环密度为1.95、1.75和1.55 g/cm3,在此基础上改变套管厚度,变化范围为0～7 mm,间隔1 mm,计算得到不同水泥环密度条件下计数比值与套管厚度的响应规律,如图6所示。

图6 不同水泥环密度下计数比值与套管厚度的响应规律Fig.6 Response law of count ratio and casing thickness at different cement ring densities

由图6可以看出不同水泥环密度条件下计数比值基本不变(最大差异小于1%),表明水泥环密度同样不影响套管厚度评价结果。

3.3 地层密度

研究水泥环密度对套管厚度评价的影响,选取地层密度分别为2.539、2.368和2.197 g/cm3,水泥环厚度和密度分别为3 cm和1.95 g/cm3,在此基础上改变套管厚度,变化范围为0～7 mm,间隔0.1 mm,计算得到不同地层密度条件下计数比值与套管厚度的响应规律,如图7所示。

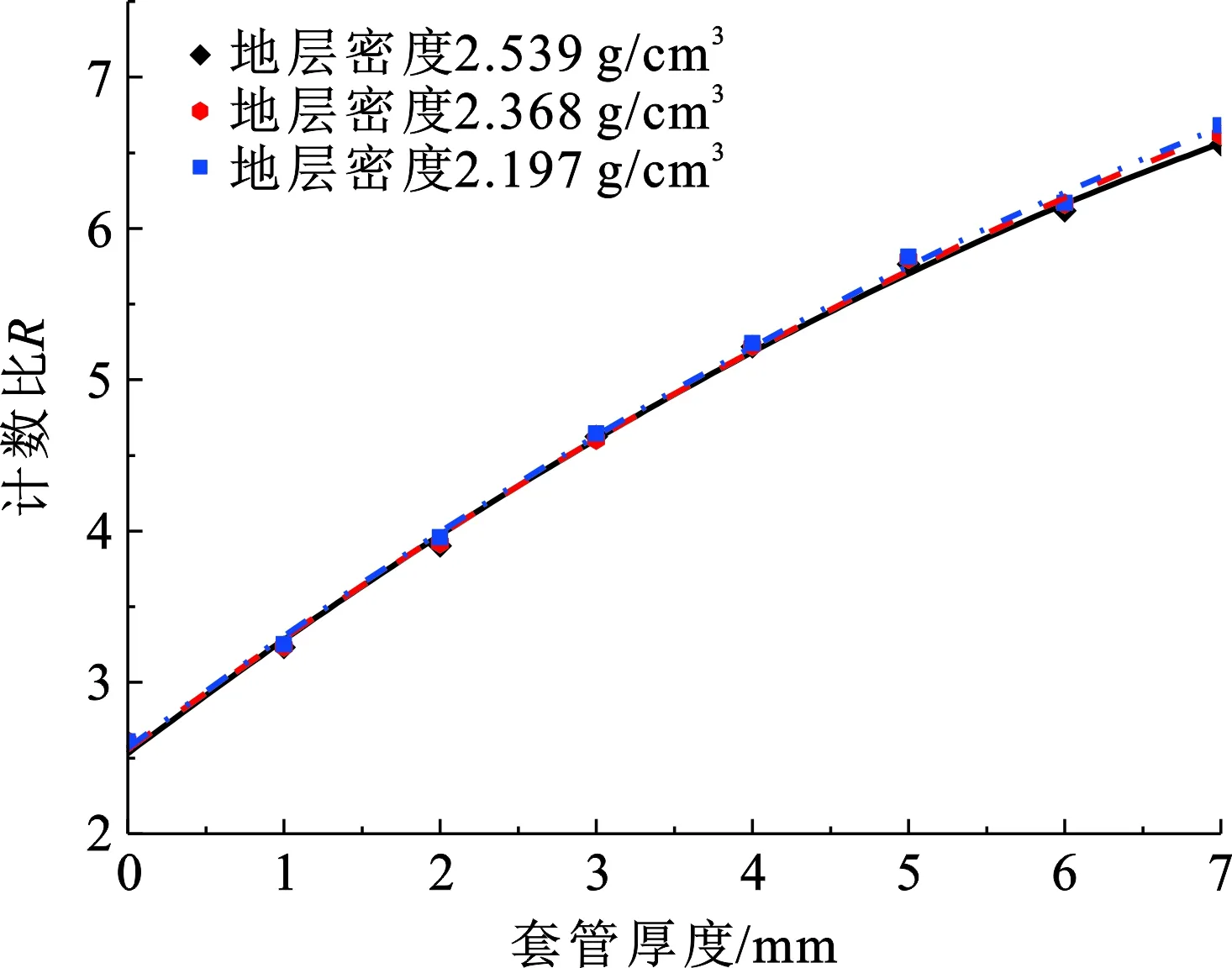
图7 不同地层密度下计数比值与套管厚度的响应规律Fig.7 Response law of count ratio and casing thickness at different formation densities

由图7可以看出不同地层密度条件下计数比值基本不变,表明地层密度不影响套管厚度评价结果。主要原因有两点:一是地层介质的光电吸收截面和康普顿散射截面远小于套管介质,因此地层密度变化时对探测器计数的影响较小;二是超近探测器的探测深度较浅,穿过套管和水泥环后与地层发生作用的伽马射线较少。

综上所述,计数比法评价套管厚度受水泥环厚度、密度和地层密度的影响较小。在井下水泥环状况未知的情况下,利用该方法可以避免水泥环参数对套管厚度评价的影响。

4 模拟实例验证

通过模拟实例进一步验证该方法的准确性。模拟井段全长4 m,地层骨架由底部至顶部分别为白云岩、灰岩和砂岩,地层密度、水泥环密度和厚度参数由图8给出。模拟井段完整套管厚度为7 mm,同时设置了4处套管缺损,从下至上发生缺损处的套管厚度分别为3、5、2和1 mm。

当仪器经过套管缺损处时,能窗Ⅰ计数增加,能窗Ⅲ计数降低,同时计数比值降低;从下至上4处缺损中心处的套管厚度计算值分别为3.2、5.3、1.9和0.9 mm,相对误差分别为6%、6%、5%和10%,完整套管处的套管厚度计算值为7.2 mm,相对误差为3%,整体套管厚度计算误差小于10%,表明该方法可以准确评价套管厚度,同时受地层密度、水泥环厚度和密度影响较小。

图8 实例模拟结果Fig.8 Results of example simulation

5 结 论

(1)基于伽马射线散射衰减规律和套管的吸收衰减特性,提出利用高能与低能窗计数比评价套管厚度的方法。该方法在消除源强影响的同时增加了套管厚度评价的灵敏度。

(2)利用蒙特卡罗方法建立井下套管-地层模型,模拟得到不同套管厚度条件下的能谱响应,分析得到光电窗能量范围为0～0.12 MeV,康普顿背散射与光电综合作用能窗范围为0.12～0.23 MeV,康普顿背散射窗能量范围为0.23～0.5 MeV。

(3)利用能窗Ⅲ与能窗Ⅰ计数比评价套管厚度的相对灵敏度最高,可以建立基于该能窗计数比的套管厚度的计算模型。

(4)不同地层密度、水泥环密度和厚度条件下的计数比基本一致,该方法受地层和水泥环参数影响较小;模拟实例表明当套管厚度为7 mm时该方法的相对误差为3%,套管厚度为1 mm时相对误差为10%,且不受地层和水泥环参数影响。