基于二维小波能量阈值的重磁数据去噪算法

索 奎,吕晓春,张贵宾,贾正元

(1.华北水利水电大学地球科学与工程学院,河南郑州 450046;2.中国地质大学(北京)地球物理与信息技术学院,北京 100083)

随着仪器和相关理论的发展,实测重磁数据精度越来越高,数据量迅速增加。由于地质构造的复杂性和仪器的非稳定性,数据包含了人文噪声、系统噪声以及数据处理引入的误差等,这类噪声具有非平稳和非线性特征[1],影响数据处理和反演的精度,甚至掩盖有效信息。线性去噪方法去除非线性噪声的效果不佳;小波变换能集中有效信号的能量,使噪声在小波域具有随机性,通过对小波系数施加某种非线性操作实现去噪,在地球物理数据处理领域应用广泛[2-6]。但小波去噪主要面临小波基函数选取[7-10],小波信噪分离阶数选取[11-13]和去噪阈值选取[13-15]3个关键问题。选择分离阶数主要有基于信号特征[16]和基于噪声特征的方法;阈值选择方法也多种多样。虽然各类方法针对不同问题提出了解决方案[17],但处理实际数据时多数情况仍依赖经验选取参数。由于模型试验参照标准确定,可以采用各种评价标准去评价去噪效果[18],解决上述3个问题;而实测数据没有参照标准,多数评价标准只能估计或作为参考,导致去噪参数选择标准不同,结果因人而异。Lyrio等[19-20]提出了一维小波变换中对3个关键问题的解决方案;索奎[21]将其扩展至二维情形,利用二维小波将重磁数据分为3个高频部分分别进行处理,从而得到更精确的结果。笔者重点研究基于能量阈值的二维小波去噪中的3个关键问题,分别针对加性噪声和乘性噪声开展模型试验。

1 小波去噪原理与方法

小波变换可将信号分解为不同频段,再利用其多分辨率的性质来研究不同尺度下每个频段的成分。与傅里叶变换相比,小波变换在时域和频域都具有良好的局部性质,能够聚焦研究对象的细节。

1.1 二维小波变换原理

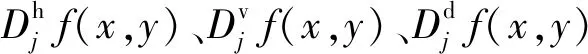
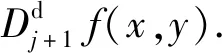
(1)

式中,j为分解尺度。

对于重磁面积数据Δg(x,y),也可以通过二维小波将总场分解为局部场(细节)和区域场(近似),n阶分解的表达式为

Δg(x,y)=A0f(x,y)=Anf(x,y)+

(2)

二维离散小波变换先利用高通滤波器和低通滤波器沿着水平(行)方向对数据进行一维分解,然后利用同样的滤波器沿着垂直(列)方向对行分解结果进行分解,二维小波3层分解如图1所示。经过3层分解,得到4种信号:水平、垂直方向均为低频的信号LL3,水平方向低频、垂直方向高频的信号LH1、LH2、LH3,水平方向高频、垂直方向低频的信号HL1、HL2、HL3以及水平、垂直方向均为高频的信号HH1、HH2、HH3。其中LL3称为逼近部分,其余3种信号称为细节部分。

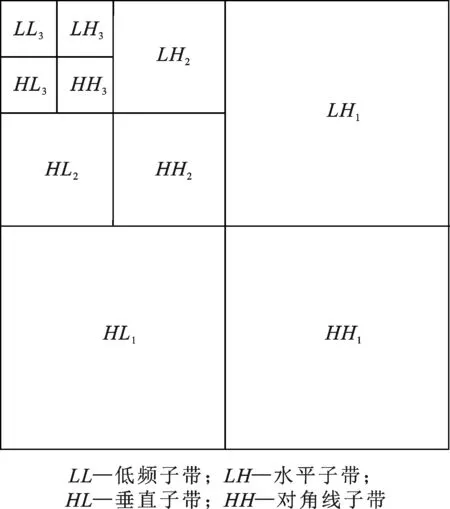
图1 二维小波3层分解示意图Fig.1 Three-level decomposition of two-dimensional wavelet

1.2 小波去噪基本原理

小波变换的能量压缩特性能够使信号变换后的大部分能量集中在少部分小波系数幅值较高的区域,即低频系数,这些区域一般是图像边缘,表示图像的主要特征。大多数噪声具有较高的频率,经过小波变换后的系数幅值很低。

小波去噪的基本原理是将含噪信号变换后的高频系数与某个阈值相比,然后按照特定的阈值函数进行修正。最后将修正后的高频系数和低频系数进行重构(逆变换),获得去噪后的信号。基于能量阈值的二维小波去噪方法仍基于上述原理。若考虑野外采集时仪器和环境影响因素,加性噪声较为符合重磁数据的特点;若考虑各项改正引起的噪声,则乘性噪声更符合数据特点。

本文中假设噪声符合高斯模型,以含加性噪声的理论模型为例进行阐述。设置包含了4个密度异常体的组合模型,参数见表1。

表1 理论模型参数Table 1 Synthetic model parameters

地面测网范围为1 023 m×1 023 m,测点点距为1 m,正演获得了1 024×1 024个重力数据,数据范围为(0.004 7～1.191 8)×10-5m/s2,如图2(a)所示,4个异常体边界较为清晰,其中2号异常体体积小,异常幅值最高,理论值等值线平滑。添加了均值为0,标准差为0.05×10-5m/s2的高斯噪声,噪声范围为(-0.234 6～0.227 3)×10-5m/s2,添加噪声后的数据如图2(b)所示,仍可以看出基本异常特征,但2号异常不显著,且等值线波动较大。

图2 加性噪声模型理论重力异常和含噪声重力异常Fig.2 Synthetic gravity anomalies and gravity anomalies with Gaussian noise

1.3 基于信噪比的基函数选择方法

小波变换前应选定小波基函数并确定分离阶数。目前小波基函数有上百种,合适的小波基函数是去噪的基础。本次研究的目标是基于能量的重力和磁场的噪声去除,要求满足含噪信号能量等于小波变换后系数能量的特性[20],即

(3)

式中,ω(j,k)为尺度j位置k处的小波系数;g(x)为空间域中位置x处的数据。

满足该特性的小波基函数必须具有正交性,常见小波基函数有Haar小波、DB(Daubechies)小波、COIF(Coiflets)小波和SYM(Symlets)小波,本文中选取的小波基函数是来源于上述几个小波族的。

多种小波基函数符合特性,因此需要选定最佳的小波基函数。选择最佳小波基函数基于信噪比,定义一个信噪比(RSN)公式[20]:

(4)

式中,ej为分解阶数j的含噪信号的高频能量;γ为最佳信噪分离阶数;J为最大分解阶数。

信噪比越大,该小波基函数去噪效果越好,本文中根据式(4)选择DB5作为小波基函数,其信噪比为1.595 4,γ为5。

1.4 信噪分离阶数选择方法

在实际数据计算时,虽然无法得知含噪信号中的噪声和有效信号的能量,但该含噪信号用同一个小波基函数进行分解时,其能量(式(3))等于噪声能量和有效信号能量之和[19]。

在不同的分离阶数时,噪声能量和有效信号能量在高频总能量的占比发生变化(图3),总体趋势是:分解阶数较低时,高频能量以噪声能量为主;随着分解阶数升高,高频能量以有效信号能量为主,二者“交叉点”处的阶数为最佳分离阶数,此处也为含噪信号的能量最低点[19-21]。基于该原理,进行信噪分离可以对含噪信号进行高阶次分解后,选择最佳阶数作为分界线,低于该阶数的小波系数全部舍去,即舍去了以噪声为主的部分,保留了有效信号为主的部分。

二维小波分解会得到3个高频信号,其中有两个信号是经过高通和低通滤波的结果,即LH和HL分量,二者含噪成分相当;一个信号是经过了两次高通滤波的结果,即HH分量,噪声成分更多,信噪分离阶数更高[21]。因此分别根据3个能量曲线确定的信噪分离阶数会有所不同,但由于对高频信号进行了更加细致的分解并分别进行了处理,因此对信噪分离更加准确。

图3为图2(b)数据进行二维小波变换后3个高频分量在1～7阶分解情形下的有效信号和理论噪声能量分布变化趋势。图3(a)为含噪信号高频能量和(LH+HL+HH)随阶数的变化,图3(b)～(d)分别是LH、HL和HH分量的能量变化。

以图3(a)为例,含噪信号能量是有效信号和噪声之和,在1～4阶分解时,其能量逐渐减小,在5～7阶分解时又迅速增大;有效信号的能量是逐步增加的,噪声则相应减小。在1～4阶时,噪声能量显著大于有效信号能量,表明此时含噪信号中以噪声为主,随着分解阶数继续增加,有效信号能量大于噪声能量,即有效信号占主要成分。从图3(b)和(c)可以看出,LH和HL分量特征较为一致,含噪数据能量最低的阶数为第4阶,HH分量噪声更多,能量最低阶数为第5阶(图3(d)),此时需要分别对1～4阶和1～5阶的小波系数置零,处理5～7阶和6～7阶小波系数即可。显然,分别对3种高频分量的数据进行去噪,能够针对不同的高频分量分别采用相应的阈值,获得更精确的处理结果。

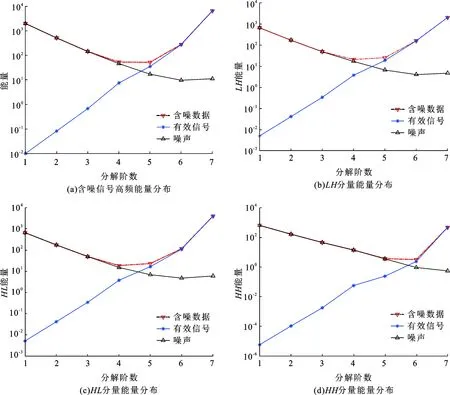
图3 合成模型重力信号和噪声在小波域不同分解阶数能量分布Fig.3 Gravity synthetic signal and noise of model energy distribution of different scales in wavelet domain

1.5 基于能量的去噪阈值选择方法

采用确定的小波基函数和分解阶数对含噪数据进行分解,再对细节部分系数进行阈值去噪。目前有多种阈值选择方法,如:通用阈值、基于Stein无偏似然估计的SureShrink阈值以及假设信号概率分布函数服从Beyes准则的BayesShrink阈值,除此之外还有多种策略的阈值选取算法,适用于各种情况。

本文中采用基于能量的阈值选取方法。由于信号变换后的大部分能量集中在少部分小波系数幅值较高、表示图像主要特征的区域,理论上只需少部分高幅值系数即可恢复大部分有效信号。选定某一个阈值,将幅值系数从大到小进行能量累加,达到阈值即认为恢复了有效信号。

以图2(b)所示含噪信号为例,将信号进行二维小波变换7阶分解后,将小波系数能量按幅值从大到小累加,能量变化曲线如图4(a)所示。可以看出,对于HL和LH分量,初期仅需20～40个高幅值系数的能量累加,总能量迅速上升到较高水平,后面虽然仍有大量系数,但能量很少,表明信号的主要能量都集中在了高幅值系数中。图中示例恢复有效信号分别使用了249和253个HL和LH系数;HH分量使用了102个系数,后续的能量仍然较大,但多是以噪声为主。

能量阈值并非越高越好,这是因为含噪信号的能量中包含了有效信号和噪声的能量,因此若选定过高的阈值既会增加计算量,也会使得恢复的信号中包含过多的噪声[21]。

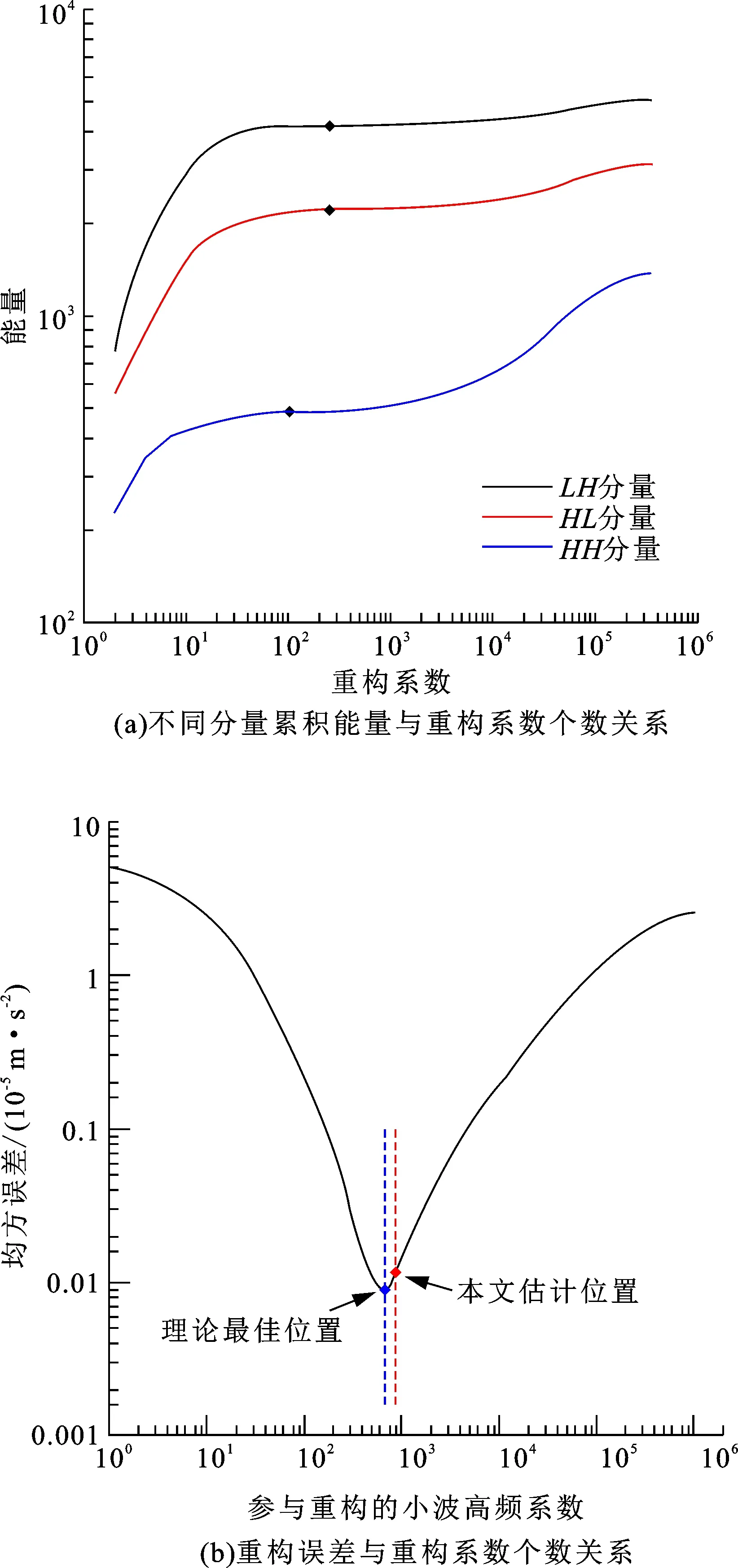
图4 能量阈值与均方误差关系Fig.4 Relationship between energy threshold and mean square error

以理论信号为标准,保持近似小波系数不变,用不同数量的细节小波系数恢复的信号与理论信号进行比对,重构信号与有效信号之间的均方误差如图4(b)所示:重构均方误差开始为5.085 6×10-5m/s2,随着重构小波系数的增加,细节信息不断增加,误差急剧减小到0.008 8×10-5m/s2,表明此时恢复的以有效信号为主,随着系数个数的继续增加,误差开始逐渐上升,直至2.588 3×10-5m/s2,表明此时恢复的信号中包含了噪声,因此与有效信号相比误差反而增大了。

从图4(b)可以看出理论最佳阈值应该在误差最小处(左侧虚线),但处理实际数据时由于不知道有效信号的准确值,无法精确确定该位置,根据式(4)确定的最佳信噪比中的能量作为阈值来确定参与重构的细节系数个数,其位置如图4(b)中的右侧虚线,此时误差并非最小,但与最佳值很接近。

基于能量阈值的二维小波去噪方法主要步骤可以总结为:①依据公式选择信噪比最大的小波基函数;②确定最佳分离阶数,计算不同阶数的能量,能量最低点即为最佳分离阶数;③确定能量阈值,最佳分离阶数及以上的能量和即为该阈值。利用本文方法对数据进行去噪,既可以得到有效信号利于进一步数据处理,也可以更准确估计噪声水平,为提高三维反演结果的精度提供依据[22]。

2 模型试验

2.1 加性噪声模型试验

为了进一步对比,本文中还对添加了标准差为0.10×10-5和0.2×10-5m/s2高斯噪声的信号进行去噪,以对比不同噪声水平的去噪结果。

针对含噪信号,本文中选择巴特沃斯低通滤波器、常规二维小波和本文方法进行去噪,去噪结果如图5所示,均方误差见表2。为了对比方便,图5插值方法及参数相同,绘图参数设置相同,绘图设置保持一致。

图5(a)～(c)为巴特沃斯低通滤波器滤波结果,均方误差分别为0.027 5×10-5、0.813 0×10-5和0.992 5×10-5m/s2,呈显著上升趋势。从图5可以看出,图5(a)具有较好的去噪效果,均方误差与小波去噪相差不大,但在1号异常体处,原本近似方形的异常等值线在去噪后变成了圆形,图5(b)和(c)也有相同情况,且均方误差与小波去噪结果已经不在同一个数量级,这表明了巴特沃斯低通滤波器局限之处。

图5(d)～(f)是二维小波去噪结果。本文中选用DB4小波,全局硬阈值去噪,此时的均方误差最低,分别为0.014 1×10-5、0.034 2×10-5和0.098 9×10-5m/s2,均显著低于巴特沃斯滤波结果。

本文中根据式(4)选择DB5作为小波基函数,最佳分离阶数为5、5和6,去噪结果如图5(g)～(i)。可以看出多数等值线曲线平滑,个别等值线有一些波动,在异常体1的附近波动最大,这是因为此处的梯度值最大,等值线最密集,总体看对异常识别没有影响。查看计算得到的噪声,符合高斯白噪声的特征,标准差为0.05×10-5m/s2,与理论值一致,这表明噪声计算较为准确。从表2可以看到3种情形本文方法均方误差均为最小,且随着噪声水平的增加,增长最慢,表明了方法的稳定性。

该试验验证了二维小波阈值去噪算法具有更小的均方误差,去除不同水平的加性噪声具有稳定性和准确性。

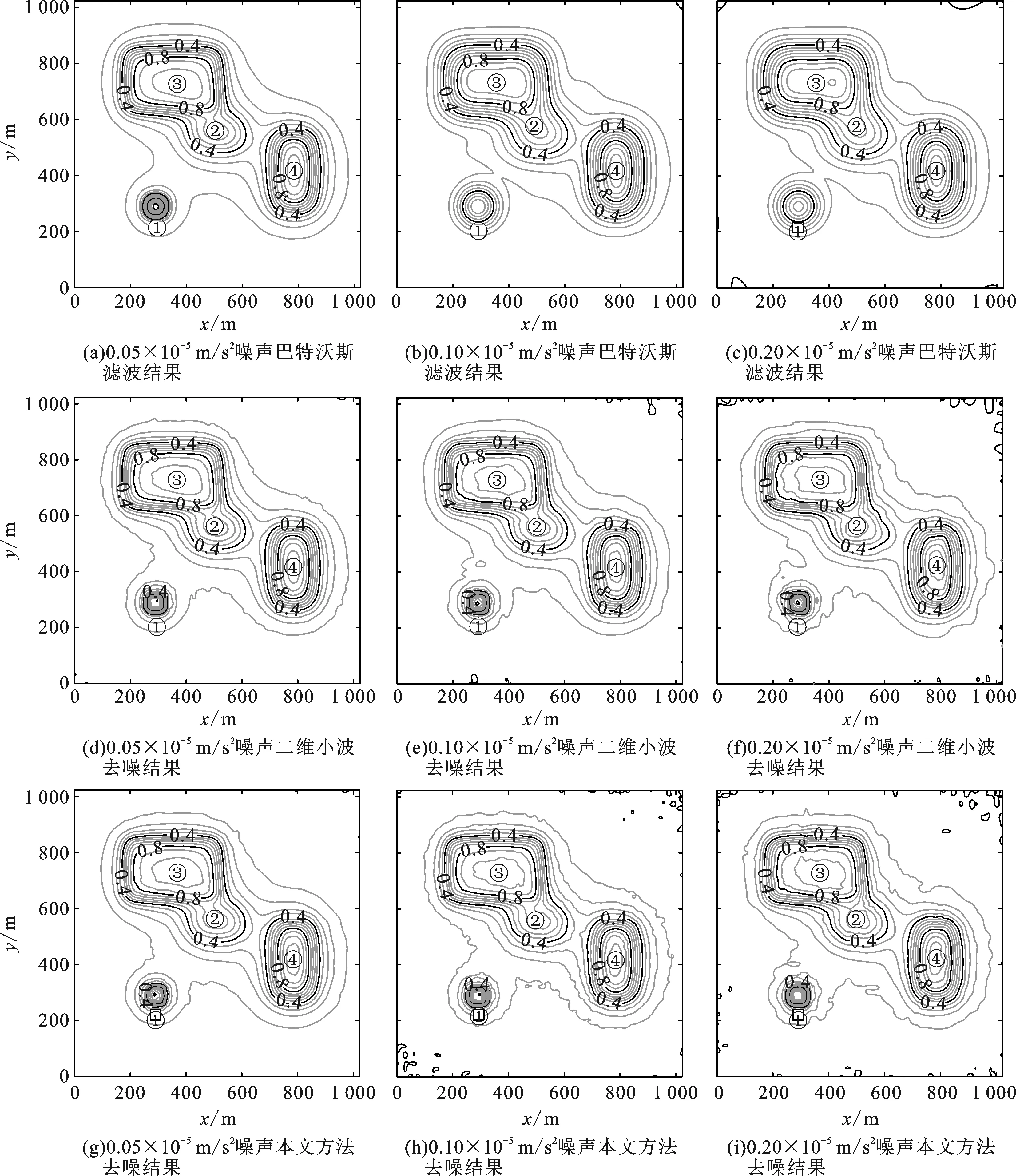
图5 模型试验加性噪声去噪结果Fig.5 Denoising result of synthetic data with additive noise

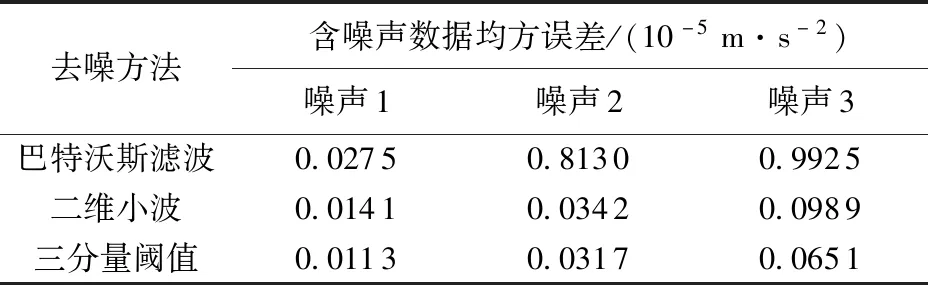
表2 不同方法模型试验去噪结果均方误差对比Table 2 Comparison of mean square error of denoising results of different methods

2.2 乘性噪声模型试验

乘性噪声模型与加性噪声模型一致,添加了3%的乘性高斯随机噪声,噪声范围(-0.135～0.135)×10-5m/s2,根据式(4)选择DB4作为小波基函数,对含噪数据进行三分量阈值去噪。最佳分离阶数为4、4和5,去噪后结果如图6。HL分量有效系数227个,LH分量有效系数263个,HH分量有效系数128个,噪声均方误差为0.007 3×10-5m/s2。

从图6(a)中可以看出,异常幅值越高,噪声幅值越高,符合乘性噪声的特征;去噪后如图6(b)所示,总体上较好地恢复了原始数据,大部分等值线曲线平滑,等值线0.05有一些波动。图6(c)和(d)分别为理论噪声和本文计算的噪声,异常体1处的噪声差别较大,此外在异常体2～4的边缘区域噪声差异也相对明显,主要集中在梯度值较大的区域,其他区域则较为“干净”,没有因为去噪算法带来人为噪声。

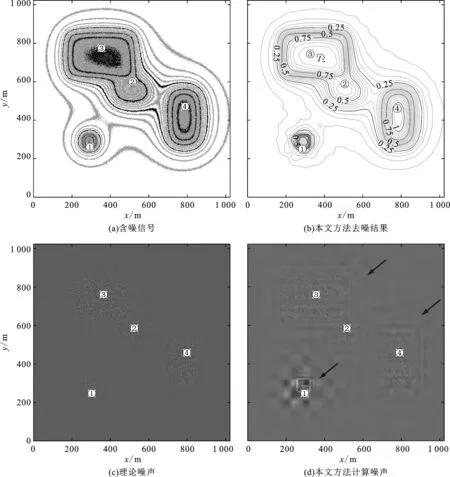
图6 模型试验乘性噪声去噪结果对比Fig.6 Denoising result of synthetic data with multiplicative noise

3 某区域实测磁异常去噪

本文中选择的实测磁异常数据位于包含多个隆起、凹陷的构造单元汇聚区,面积约1 100 km2,磁异常变化范围大,有异常变化剧烈区和相对平静区,部分区域有人类活动引起的人文噪声。

磁异常数据分辨率为250 m×500 m,磁异常值范围为-654.77～1 477.21 nT,原始数据如图7(a)所示,可以看出,图右侧有本区域面积最大、幅值最高的磁异常区,中部和左侧有部分小范围磁异常,磁噪声使部分区域形成了小范围假异常区,等值线较为复杂。本文中分别采用巴特沃斯低通滤波、二维小波去噪、本文去噪方法3种方法分别进行去噪处理。3种方法去噪结果如图7(b)～(d)所示,为方便对比,采用相同的绘图参数。

图7(b)为采用巴特沃斯低通滤波器进行低通滤波结果,参数为8阶,截止波长1 000 m。可以看出,线性滤波器的处理后等值线变得圆滑,高频噪声得到了较好的去除,数据范围-496.72～1 475.98 nT,表明了对显著的高值有较好的保幅效果,但对异常范围小的负值则有较为明显的“损失”,在箭头指示区域对部分异常的圆滑有一些过度,这与图5(a)～(c)中对1号异常图产生的圆滑效果类似。去噪结果对于定性认识够用,但随着三维反演算法的发展,对原始数据处理的要求是在去噪的同时尽可能保留“原始信息”,显然巴特沃斯低通滤波器在滤除噪声的同时损失了过多的细节信息。

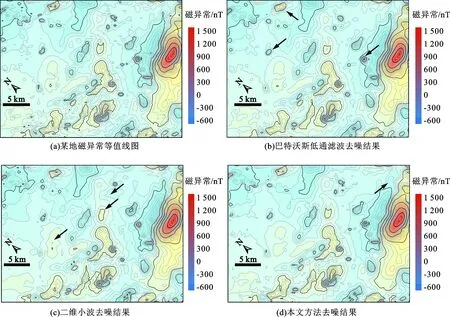
图7 某地实测磁异常去噪结果对比Fig.7 Comparison of denoising results of measured magnetic anomalies in a certain area

图7(c)为采用全局硬阈值二维小波去噪结果。与图7(b)相比,小波滤波结果更接近原始图像,对数据的圆滑效果不显著,数据范围-584～1 439 nT,除了对负值的“保护”有了显著提升外,对显著高值也有了较好的保幅效果。当然,对正负异常幅值的“保护”并不能直接说明去噪效果的优劣,但从反演计算对数据的要求角度看,图7(c)显然保留了更多的细节信息。同时存在一些问题,在部分区域特别是箭头指向区域,与原始数据的差异较为明显,对个别小范围异常出现了滤除,可能是阈值选取的原因。

图7(d)为使用本文方法去噪结果。使用DB3小波进行处理,进行二维小波变换前x、y方向数据需延拓到128个。本文中采用点对称边界延拓方法,边界处理的目的是保留小波的重组性,尽量减少边块效应。前人研究结果显示,相较于广泛应用的对称延拓、周期延拓,点对称延拓精度高于对称延拓[23]。3个高频分量最佳分离阶数为2、2和3阶,数据范围-617～1 462 nT。与图7(c)较为一致,从数据范围看对正负异常幅值“保护”更优,较为显著的是图中3个箭头指向的区域,在去除高频噪声的同时与原始数据保持较好的一致性,表明了本文提出的方法对于二维重磁数据具有更好的适用性。

从实际区域磁数据去噪和模型对比试验结果来看:对于大范围显著异常,多数算法的滤波结果差异不大,能够在去除噪声的同时保持原始异常形态;但对于弱异常的处理则有较大差异,线性滤波通常会出现过度圆滑的情形;二维小波更能适应实际数据非线性非平稳的特点,则能够在保持异常幅值的同时去除大部分噪声,这对于反演计算有较为重要的意义。

4 结 论

(1)二维小波能量阈值去噪算法去除噪声的相对误差小于常规二维小波和线性滤波器,且能够保持异常形态不失真,有利于弱异常信号的识别和提取。

(2)含噪信号经二维小波分解后,在3个高频成分中噪声随分解阶数的增加能量降低,有效信号则相反。

(3)二维小波能量阈值去噪算法中,小波基函数和去噪阈值的确定依据信噪比公式,最佳信噪分离阶数为信号的能量最低阶数,3个关键参数选取有客观依据,避免了依据经验选择参数。