掺氢天然气管道的分层现象

刘翠伟,崔兆雪,张家轩,裴业斌,段鹏飞,李璐伶,杨宏超,李玉星

(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580;2.西安长庆科技工程责任有限公司，陕西西安 710018;3.深圳市燃气集团股份有限公司,深圳 518000)

随着全球绿色低碳经济的发展,发展清洁能源是必然选择,而氢能具有清洁无碳、绿色高效、可再生、应用模式丰富等优势[1],被视为21世纪最具有发展潜力的“终极能源”[2],将在实现“碳中和”和绿色可持续发展中扮演重要角色[3-4]。大力发展氢能的过程中,氢气的大规模、长距离、低成本储运是急需解决的关键难题,近些年国内外提出将氢气按照一定比例掺入现役天然气管道中混输的输氢方式[5-7]。然而,由于氢气和甲烷的密度差别很大,常温常压下甲烷密度约是氢气的8倍,且氢气比天然气更易扩散[8]。随着氢气的掺入,掺氢天然气在存储和管道停输过程中在重力作用下会出现体积分数分布不均匀现象。同时在掺氢天然气管道运行过程中,当管道流速较小时也有可能发生氢气向管道顶部偏移的现象[9]。任少云等[10-12]通过数值模拟和实验验证的方法,针对储罐和管道内甲烷-空气、氢气-空气、丙烷-空气等混合气体的混合过程,对气体体积分数分布规律进行研究,研究结果表明储罐和管道内混合气体体积分数分布不均匀,导致储罐和管道内垂直方向上体积分数出现分层现象。陈俊文等[9]对掺氢天然气在带压运行下的起伏管和直管停输分别进行了模拟,得到起伏管道的高凸处氢气体积分数升高,而低凹处甲烷体积分数升高的规律;直管道的管道截面也出现了非常明显的氢气分层。这些研究在一定程度上证实了混合气体体积分数分布不均匀现象的存在,但仍然存在两个问题:一是对氢气-甲烷的分层现象考虑较少,且研究不深入,没有得到不同影响规律下的氢气体积分数分布规律;二是几乎未考虑管道流动状态时的氢气分层现象。虽然氢气掺入天然气管道进行输送具有诸多优势,但氢气的掺入会给天然气管道带来氢脆、氢致开裂等管材失效风险[13-15]。Melaina等[16]指出氢气对管道的损伤程度受到氢分压的影响。氢分压是掺氢天然气管道、储气瓶选材的重要考虑因素,控制合理的氢分压是掺氢天然气管道安全设计的基础,而掺氢天然气中氢气体积分数的分布不均匀会影响储气瓶和管道不同位置的氢分压。因此有必要深入探究掺氢天然气的分层问题,同时不同掺氢比例的掺氢天然气的泄漏率、燃烧速率、热能及爆炸强度不同[17],分层对于掺氢天然气管道的泄漏后果分析以及安全距离的确定也有一定影响。因此笔者采用数值模拟的方式研究掺氢天然气的分层现象,明确掺氢天然气在储气瓶、管道停输及流动状态下的氢体积分数分布规律。

1 数值模拟方法

1.1 数学模型

掺氢燃气分层研究主要涉及到的数学模型为多相流混合模型和气体湍流模型,湍流模型采用标准k-ε模型。

1.1.1 混合(Mixture)模型

Mixture模型用于模拟不同速度的流体运动。采用分压法向密闭空间内充入气体,两种气体的密度和速度各不相同,通过混合物模型描述多种不同物质混合,求解掺氢天然气分层过程的控制方程为

(1)

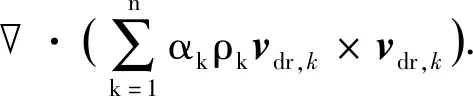
(2)

其中

式中,ρm和ρk分别为混合物密度和第k相密度,kg/m3;t为时间,s;vm和vk分别为混合物平均速度和第k相的速度,m/s;αk为第k相(氢气和天然气)的体积分数;n为相数;μm和μk分别为混合物动力黏度和第k相动力黏度,Pa·s;vdr,k为漂移速度,m/s;p为静压,Pa;g为重力加速度,m2/s。

1.1.2 湍流模型

湍流模型选用标准k-ε模型,表示为

(3)

其中

式中,k为湍流动能;ε为湍流动能耗散率;μt为湍动黏度;Gk为由层流速度梯度而产生的湍动能;Gb为由浮力产生的湍动能;YM为在可压缩湍流中扩散产生的波动,其中σk=1.0,σε=1.3,C1ε=1.44,C2ε=1.92,Cμ=0.09。

1.2 数值方法验证

任少云等[11]对甲烷-空气混合气体在容器内的静置混合过程进行试验研究,发现混合气体静置后在竖直方向上出现体积分数非均匀分布,即分层现象。为证明本文建立的掺氢天然气分层模型的可靠性,建立与文献中实验装置完全相同的物理模型。模拟采用多相流Mixture模型,SIMPLE算法、瞬态计算和参数设置与实验完全相同;计算过程中不考虑与外界的传热,管壁为绝热壁面边界;将混合气体静置5 min后不同高度处的甲烷体积分数模拟值与实验值进行对比,如图1所示。

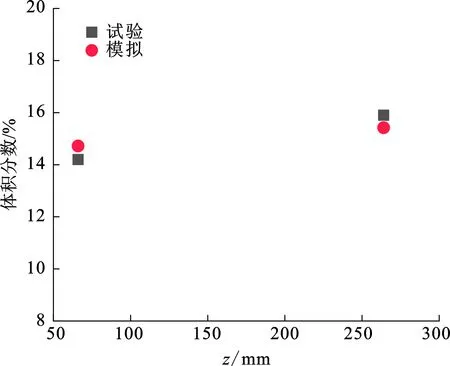
图1 不同高度处甲烷体积分数模拟值与试验值对比Fig.1 Comparison between simulated and experimental values of CH4volume fraction at different heights

由图1可知,模拟值与试验值可以较好吻合,最大误差仅为3.662%。因此可以认为采用该数值模拟方法对掺氢天然气的混合扩散和分层现象进行模拟研究是可行的。

2 储气瓶气体分层

2.1 仿真模型

储气瓶模型直径为100 mm,高度为300 mm,距离气瓶顶部60 mm处设直径10 mm的充气口,z轴反方向为重力方向,模型采用三维四面体非结构化网格,充气口处网格加密,如图2所示。采用多相流混合模型,充气口设为压力入口,按照分压法分别充入体积分数87%甲烷和体积分数13%氢气,可压缩理想气体,当储气瓶内总压达到1 MPa时,充气口设为wall,关闭充气口,开始静置气体。分别在储气瓶顶、中、底部设置监测点S1(0,0,0.28),S2(0,0,0.15),S3(0,0,0.02),单位均为m。

图2 储气瓶模型Fig.2 Gas cylinder model

对模型进行网格独立性验证,分别采用3种尺寸的网格进行模拟:3 mm×3 mm×3 mm(网格1),5 mm×5 mm×5 mm(网格2),10 mm×10 mm×10 mm(网格3),网格总数依次为279 199、84 946、21 542。得到储气瓶中心监测点S2的氢气体积分数变化曲线如图3所示。

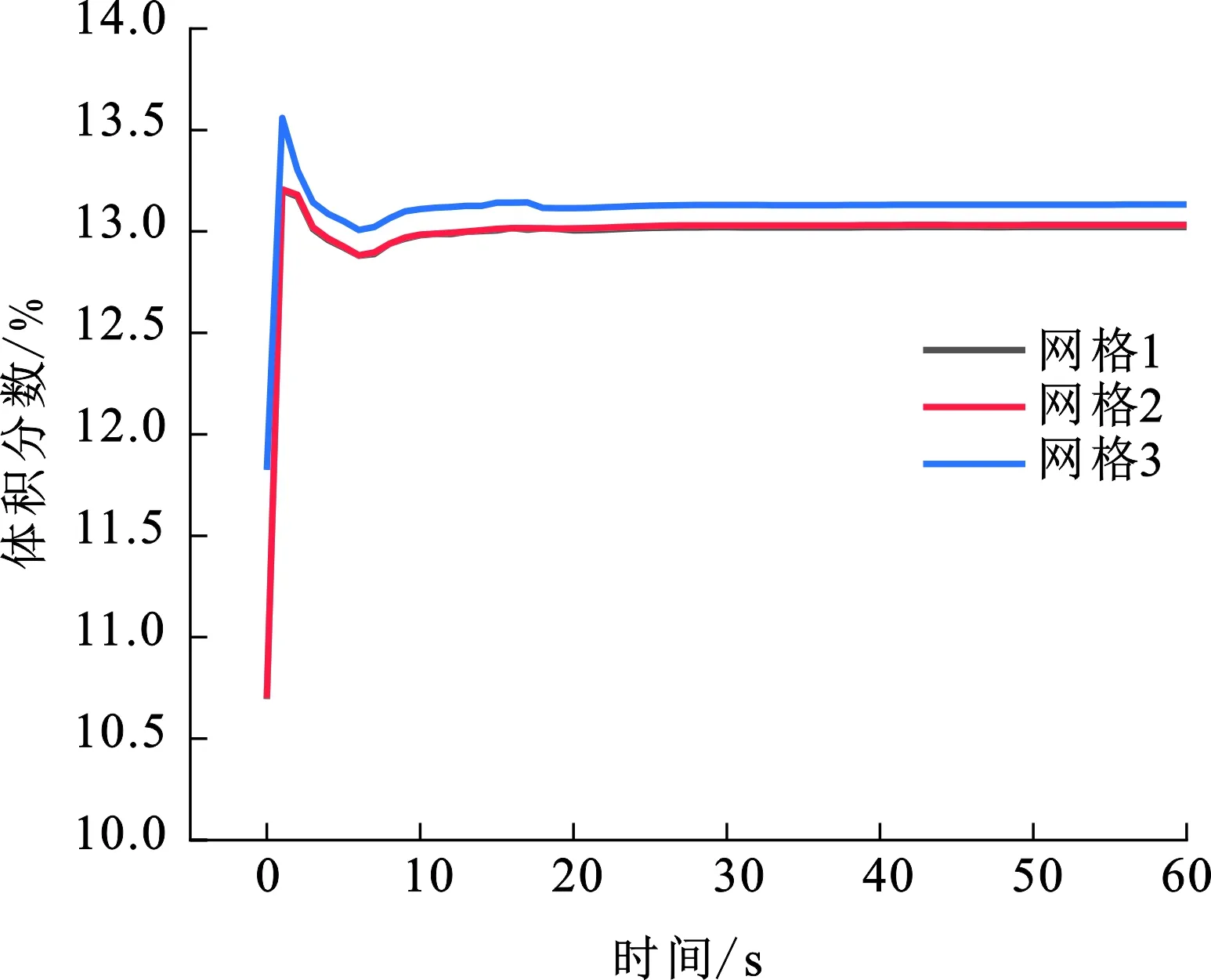
图3 网格独立性验证Fig.3 Grid independence verification

由图2可知,网格1和网格2的氢气体积分数随时间的变化曲线基本重合,而网格3的偏差较大。同时考虑到若网格太密,占据的计算资源较大,因此选择5 mm×5 mm×5 mm(网格2)进行模拟,得到不同静置时间的氢气体积分数云图和各监测点的氢气体积分数曲线如图4、5所示。

由图5可知,储气瓶完成充气开始静置时,混合气体体积分数随静置时间逐渐稳定,但是储气瓶顶部的氢气体积分数大于13%,中部的氢气体积分数约在13%,底部的氢气体积分数低于13%。说明充气完成后,气体通过分子运动达到混合均匀的目的,但是因为氢气和甲烷的密度差别很大,在重力作用下,密度差引起的氢气体积分数分布趋势比分子运动的混合均匀趋势更显著,因此出现了气体分层现象,密度小的氢气逐渐在储气瓶顶部聚集,甲烷在储气瓶底部聚集,导致储气瓶顶部氢气体积分数大于气瓶底部氢气体积分数。这与任少云[11]研究得到的气体体积分数变化趋势和结论一致,进一步验证了该模型和数值模拟方法的可靠性。

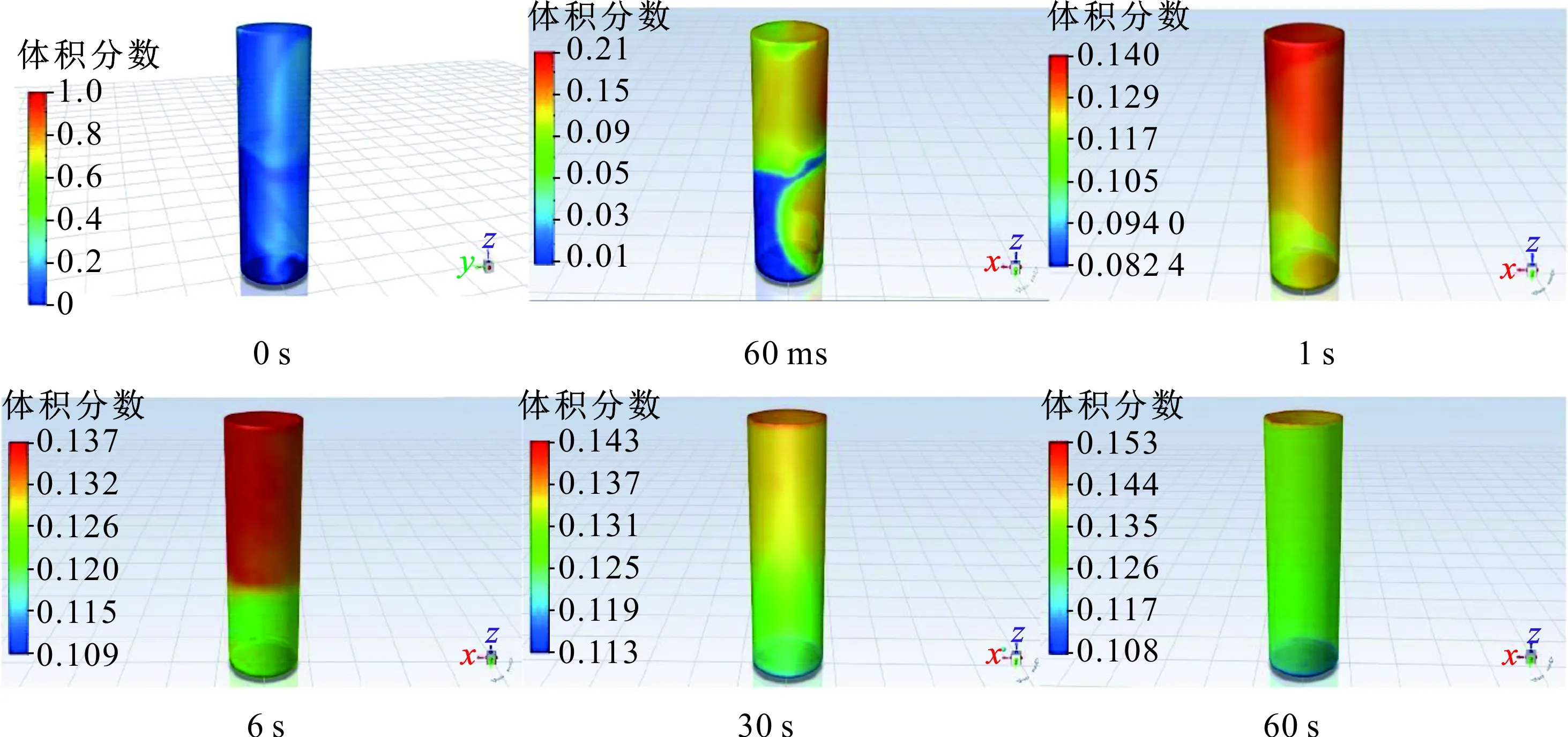
图4 充氢过程氢气体积分数云图Fig.4 H2 volume fraction contours during hydrogen mixing process

图5 充氢过程储气瓶顶、中、底部氢气体积分数Fig.5 H2 volume fraction at the top,middle and bottom of gas cylinder during hydrogen mixing process

2.2 储气瓶分层

采用分压法向储气瓶内充气,由于两种气体的密度差别大,软件模拟时间有限,气瓶内气体始终不能完全混合均匀。因此为进一步研究储气瓶中混合气体的分层问题,初始使储气瓶内充满体积分数分布均匀的混合气体(氢气体积分数30%),储气瓶内压力为1 MPa,关闭充气口开始静置,随静置时间氢气体积分数变化和云图如图6、7所示。

由图6、7可知,气体静置过程中,大约在35 min时储气瓶顶部和底部监测点的氢气体积分数发生明显变化,气瓶顶部的氢气体积分数逐渐上升,大于初始氢气体积分数(30%),底部的氢气体积分数逐渐下降,远低于30%,中间监测点的体积分数稳定在30%。储气瓶内气体体积分数出现分层现象,密度小的氢气上升积聚在气瓶顶部,密度大的甲烷下沉聚集在气瓶底部。

图6 初始体积分数均匀时储气瓶顶、中、底部氢气体积分数Fig.6 H2 volume fraction at the top,middle and bottom of gas cylinder at the same initial volume fraction

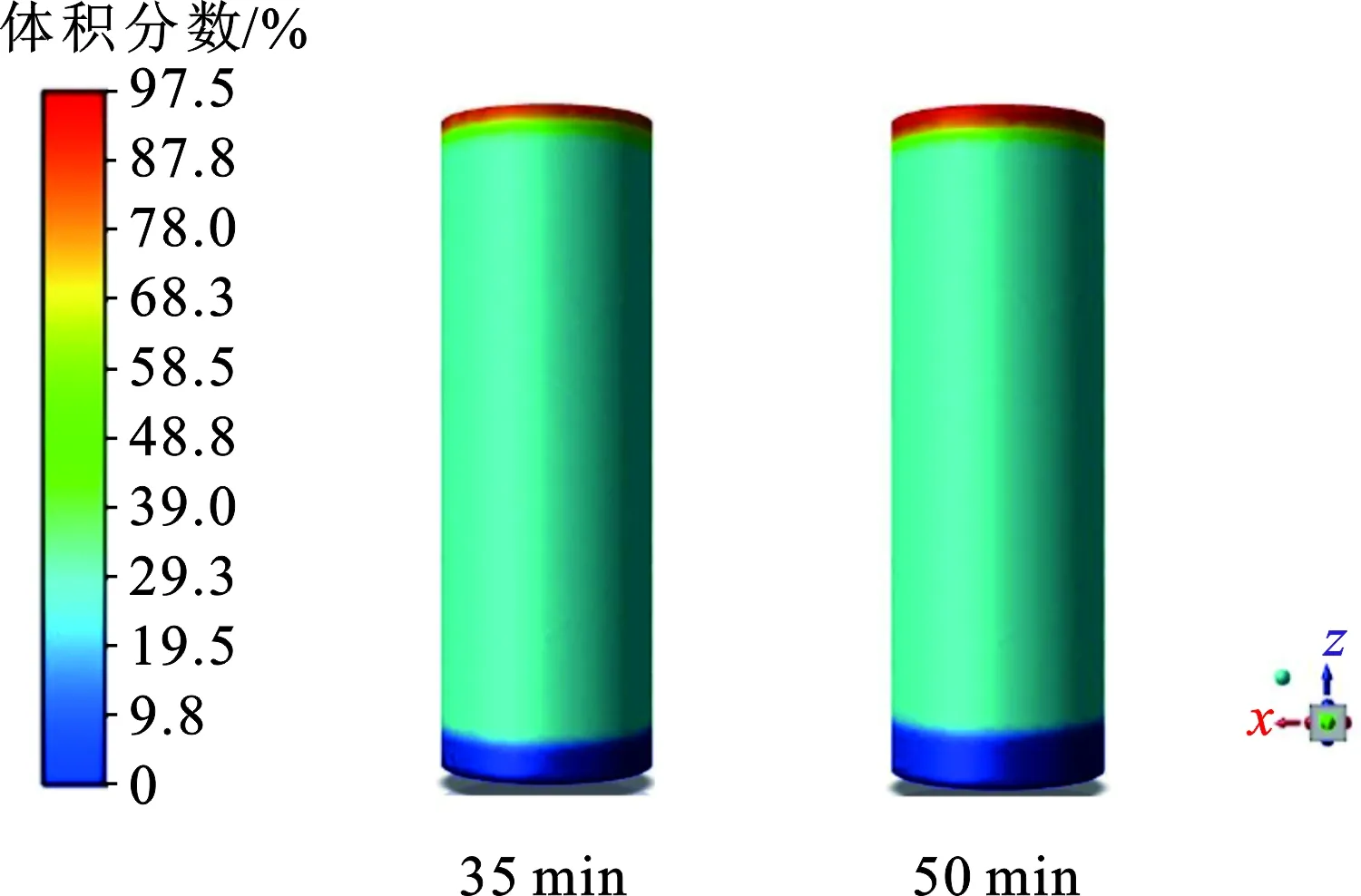
图7 初始体积分数均匀时氢气体积分数云图Fig.7 H2 volume fraction contours at the same initial volume fraction

通过储气瓶仿真模型的建立及文献对比,验证了所建立的分层模型的有效性,进一步研究掺氢天然气在管道中的分层现象。

3 管道气体分层

管道模型采用三维六面体结构化网格,通过网格独立性验证选择30 mm×30 mm×30 mm的网格尺寸,z轴的反方向设为重力方向,管道模型如图8所示。

图8 管道长度4 m、管径800 mm管道模型Fig.8 Pipe model with length of 4 m and diameter of 800 mm

3.1 管道停输静置分层

基础工况模型参数为管道长度4 m,管径800 mm,在管道顶部、中心、底部、起点、终点分别设置氢气体积分数监测点S1(2,0,0.38),S2(2,0,0),S3(2,0,-0.38),S4(0,0,0),S5(4,0,0),单位均为m。管内充满混合均匀的甲烷-氢气混合气体,其中氢气和甲烷体积分数分别为10%和90%;管道压力为1 MPa,温度为293 K,管道两端进出口设置为wall,开始静置气体,进行非稳态计算。

3.1.1 分层现象

当管道压力为3 MPa,其余参数设置同基础工况时,气体静置过程中,各监测点氢气体积分数变化曲线和云图如9、10所示。可以看出,管道停输后,在甲烷-氢气混合气体静置过程中,管道内出现分层现象,氢气上浮在管道上方积聚,甲烷下沉在管道底部积聚,随着静置时间增加,管内的分层现象更加明显;大约在40 min,氢气体积分数分布逐渐稳定,管道顶部氢气体积分数大约是底部氢气体积分数的10.811倍。同时在管长中心线方向的监测点S2、S4和S5的氢气体积分数变化基本一致,均与氢气在管道中的初始体积分数(10%)相差不大,这也说明氢气在管长方向的体积分数分布均匀,仅在管径方向由于重力出现分层。这也与文献[11]中气体混合后受重力作用,管道内垂直方向上体积分数出现分层现象的结论一致。

图9 氢气体积分数变化曲线Fig.9 H2 volume fraction curves

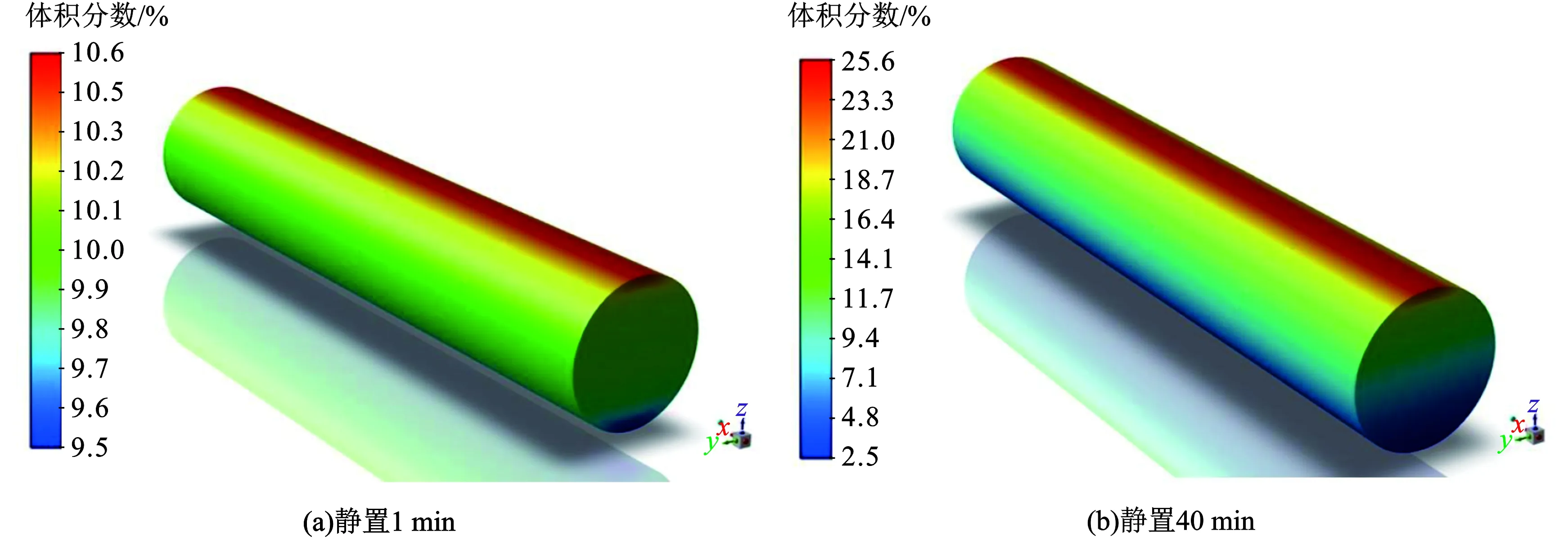
图10 停输静止氢气体积分数云图Fig.10 H2 volume fraction contours when pipe being cut off

3.1.2 影响因素

基于初始工况,分别改变压力、管径、温度和掺氢比进行停输静置模拟,压力分别为1、3、5 MPa,管径分别为600、800、1 000 mm,温度分别为273、293、313 K,掺氢比分别为10%、20%、30%。气体静置40 min时,氢气体积分数云图、管径方向氢气体积分数分布如图11、12所示。

由图11、12可以看出,压力、管径、温度和掺氢比对分层程度的影响。

(1)压力。管道压力越大,管道重力方向氢气体积分数梯度越大,分层现象越明显;当管内压力为1、3、5MPa时,管道重力方向体积分数梯度分别为15.3%/m、28.8%/m、37.7%/m;且压力越大,氢气体积分数达到稳定分布的时间越短。

图11 静置40 min时氢气体积分数云图Fig.11 H2 volume fraction contours after 40 mins

图12 静置40 min时管径方向氢气体积分数分布Fig.12 H2 volume fraction distribution in pipe diameter direction after 40 mins

(2)管径。管径越小,管道重力方向的氢气体积分数梯度越大,分层现象越明显;当管径为600、800、1 000 mm时,管道重力方向体积分数梯度分别为20.7%/m、15.3%/m、12.5%/m;但是每种管径顶部最大氢气体积分数相等,底部最小氢气体积分数也相等;随着管径增大,离管中心相同距离处的氢气体积分数分布越均匀,分层现象越不明显。

(3)温度。温度越低,管道重力方向氢气体积分数梯度越大,分层现象越明显;当气体温度为273、293、313 K时,管道重力方向体积分数梯度分别为16.1%/m、15.3%/m、14.6%/m,这是由于随着温度增加,气体分子能量增加,分子布朗运动加剧,气体混合更充分,越不易出现分层。

(4)掺氢比。掺氢比越大,管道重力方向氢气体积分数梯度越大,分层现象越明显;掺氢比为10%、20%、30%时,管道重力方向体积分数梯度分别为15.3%/m、21.0%/m、23.3%/m。

3.2 管道运行状态分层

3.2.1 分层现象

模型管道长度为10 m,管道直径为600 mm。边界条件:管道入口为速度入口,设为2.5 m/s,管内气体为混合均匀的甲烷-氢气,其中氢气和甲烷体积分数分别为10%和 90%;管道出口为压力出口,设为1 MPa,温度273 K,稳态计算。模拟得到氢气体积分数和压力云图如图13所示。

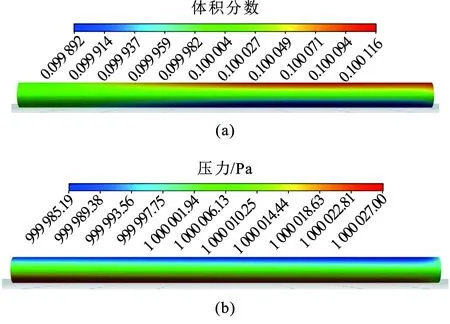
图13 氢体积分数和压力云图Fig.13 H2 volume fraction and pressure contours

由图13可以看出,掺氢天然气管道运行中,随着气体的流动,管内气体从一开始的均匀分布逐渐开始发生分层现象,氢气向管道顶部漂移,形成管道顶部氢气体积分数大,底部氢气体积分数小的分层现象。由压力云图可以看出,管道顶部的压力小于底部压力,这是由于管道流速很小,管道较短,管道运行中压降很小,同时掺氢天然气发生分层,管顶聚集密度小的氢气,管底聚集密度大的甲烷,造成管道压力分布也出现分层,顶部压力小,底部压力大。

3.2.2 影响因素

为深入研究管道运行中管内掺氢天然气的分层现象,研究压力、流速、温度和掺氢比对分层的影响,针对不同工况进行模拟得到氢气在重力方向的最大和最小体积分数及体积分数梯度见表1。管道出口处管径重力方向氢气体积分数分布见图14。

(1)温度。温度越低,管道重力方向氢气体积分数梯度越大,分层现象越明显。这是由于温度低抑制了气体分子运动,混合气体不能充分混合均匀,由于重力作用在管道重力方向出现体积分数分层。

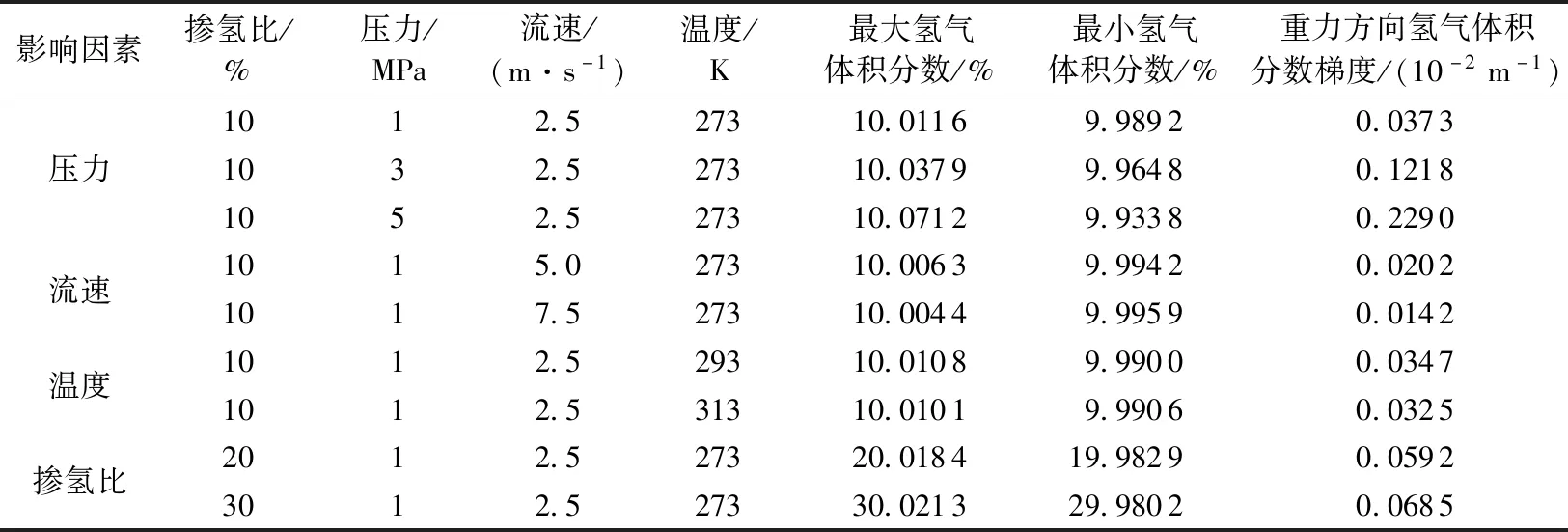
表1 模拟结果Table 1 Simulation results

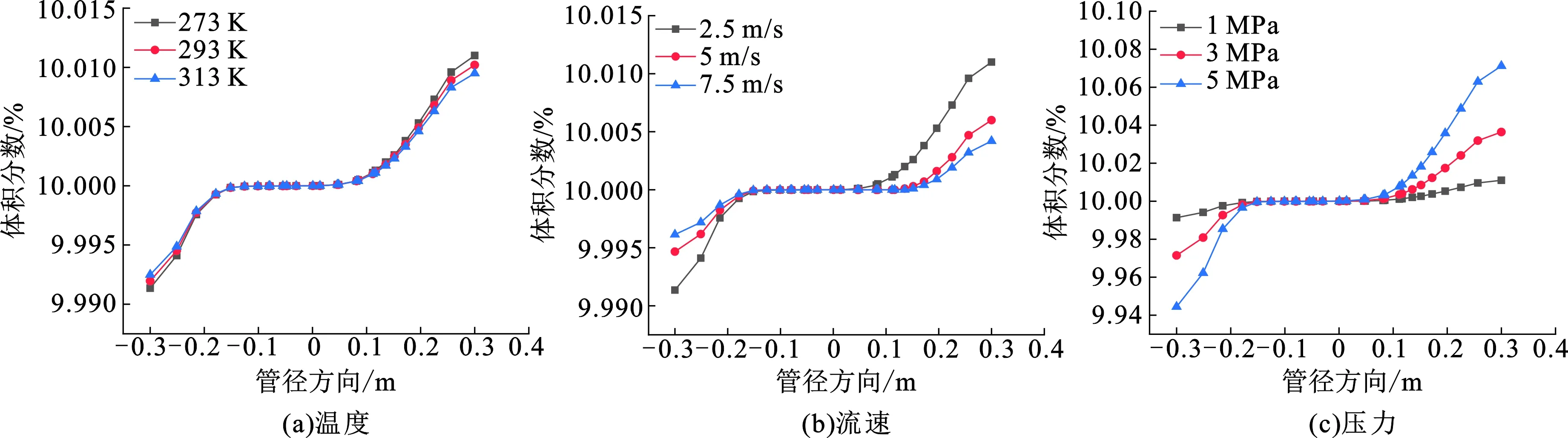
图14 管径方向氢气体积分数分布Fig.14 H2 volume fraction distribution in pipe diameter direction

(2)流速。当气体流速很小时,氢气逐渐向管道顶部积聚,出现了明显的分层现象。随着气体流速增加,管径方向氢气体积分数变化特别小,基本混合均匀。因此掺氢天然气管道适宜以高流速运行。

(3)压力。管道压力越大,管径方向氢气体积分数梯度越大,分层现象越明显。为避免气体分层,掺氢天然气管道适宜在低压下运行。文献[18]-[19]中研究表明掺氢天然气管道在低压下运行时,氢气与天然气具有相同的泄漏率,氢气不会优先从天然气管道泄漏,这也验证了本文结论的正确性。

4 结 论

(1)掺氢天然气存储在储气瓶中时,随着静置氢气体积分数在重力方向出现分层现象。

(2)掺氢天然气管道停输后,随着静置氢气逐渐上浮到顶部,甲烷下沉到管道底部,出现明显的分层现象,当静置时间达到某一值后,氢气-甲烷体积分数分布趋于稳定,但仍然存在体积分数梯度;且随着压力和掺氢比增大,温度和管径减小,重力方向氢气体积分数梯度越大。

(3)掺氢天然气管道以非常小的流速运行时,氢气随着流动逐渐向管道顶部偏移,管道重力方向也会出现分层现象,但相比于停输管道,氢气体积分数梯度特别小;且在低温、高压工况下运行时,更易出现气体体积分数分层。

(4)掺氢天然气管道适宜低压高速运行,此时安全风险较小。