三角形几何场景，数学文化新情境

徐 俊

(江苏省扬州市江都区育才中学，江苏扬州，225200)

弘扬传统数学文化，是近年新高考数学试卷中的一大热点与亮点，也是落实新高考数学考纲的一个明确体现.特别地，以三角形这一简单的平面几何图形为几何场景，结合高中数学知识创设数学文化情境成为高考数学命题的一个新的“增长点”，倍受各方关注.

1 黄金三角形

( )

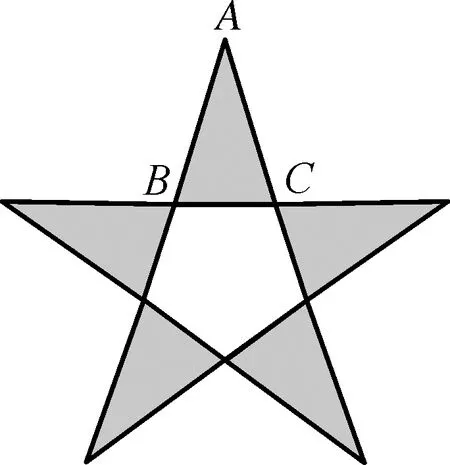
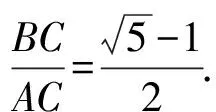
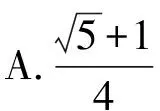
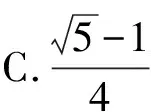
分析：根据题目条件，直接利用黄金三角形的定义，综合初中平面几何与三角函数的知识，通过诱导公式以及二倍角公式的应用来分析与求解.

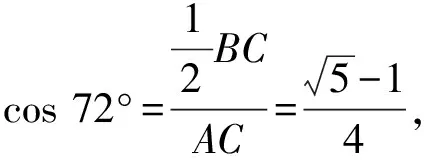
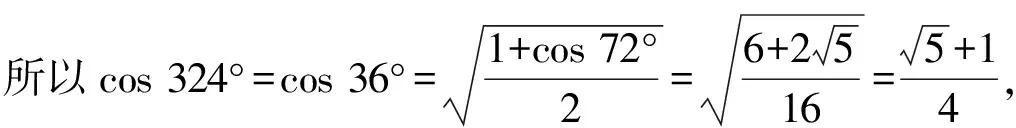
点评：此类创新情境与综合应用问题，实质是一个初中的平面几何问题的深入与拓展.本题“新瓶装旧酒”，以数学文化为问题情境，借助平面几何图形直观展示三角形的边、角关系以及对应图形的特征，进而得以求解相关角的余弦值问题.

2 费马点

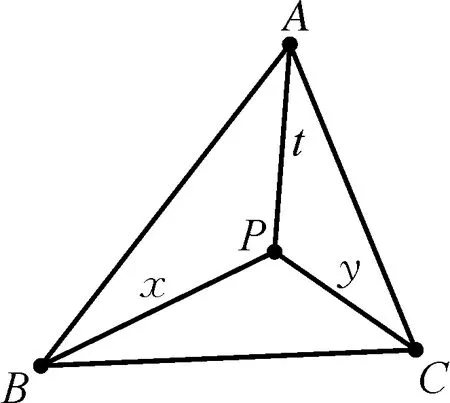
例2(江西省景德镇市2022届高三第二次质检理科数学试卷·16)1643年法国数学家费马曾提出了一个著名的几何问题：已知一个三角形，求作一点，使其到这个三角形的三个顶点的距离之和为最小.它的答案是：当三角形的三个角均小于120°时，所求的点为三角形的正等角中心(即该点与三角形的三个顶点的连线段两两成角120°)，该点称为费马点.已知△ABC中，其中∠A=60°，BC=1，P为费马点，则PB+PC-PA的取值范围是.

分析：本题是一道以三角形“费马点”为背景的解三角形问题，问题的求解其实是一个多元代数式最值的求解过程.解题思路是先根据题中的条件建立三个变量PA，PB，PC之间的等量关系(多元约束条件)，进而通过消元和函数的方法求解多元代数式的取值范围.

解析：方法1(解三角形法)设PB=x，PC=y，PA=t，

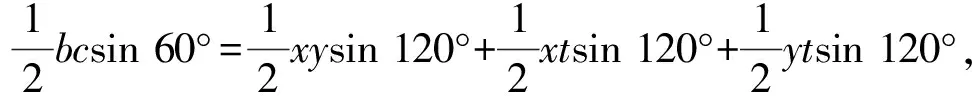
整理有bc=xy+xt+yt，①

在△PAC中，由余弦定理，可得b2=y2+t2-2ytcos 120°=y2+t2+yt，②

在△PAB中，由余弦定理，可得c2=x2+t2-2xtcos 120°=x2+t2+xt，③

在△ABC中，由余弦定理，可得a2=b2+c2-2bccos 60°，即b2+c2-1=bc，④

将①、②、③ 代入④，可得(y2+t2+yt)+(x2+t2+xt)-1=xy+xt+yt，

整理可得x2+y2+2t2-1=xy，⑤

在△PBC中，由余弦定理，可得a2=x2+y2-2xycos 120°，即x2+y2+xy=1，⑥

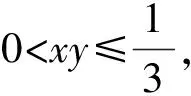
由⑤与⑥，整理可得t2=xy，

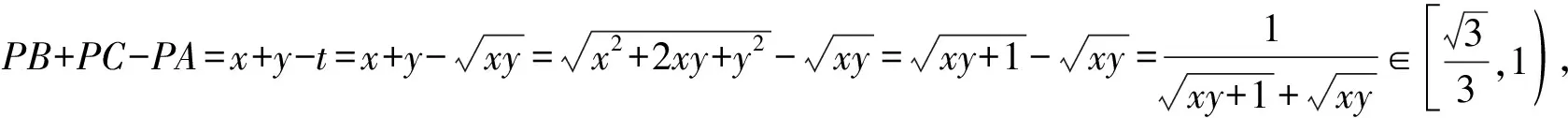
点评：根据题目条件，通过余弦定理和三角形的面积建立多个方程，化简整理出变量间的关系x2+y2+xy=1和t2=xy，再由代换，变量变换，辅以基本不等式的应用以及配凑法，将多元变量问题转换为单变量问题，最后利用函数的性质来分析与求解.解决此类多元最值问题的一般套路：整体代换、消元处理或换元处理等.

方法2：(平面几何法)设PB=x，PC=y，PA=t，设∠BAP=α，

则知∠ABP=∠CAP=60°-α，可得△ABP∽△CAP，

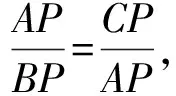
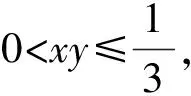
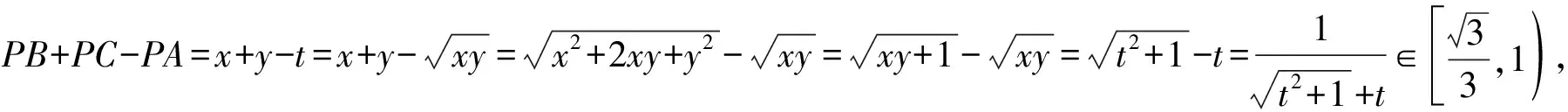
点评：根据题目中的几何图形的性质特征，通过两个三角形相似找到变量间的关系，可以有效简化数学运算.对于多元代数式的取值范围问题，可以利用整体代换或换元，将多元变量关系转化为一元函数问题来分析与处理，实现问题的巧妙转化.

3 欧拉线

例3(辽宁省名校联盟2022届高三10月份联合考试数学试卷·11)(多选题)著名数学家欧拉提出了如下定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，此直线被称为三角形的欧拉线，该定理被称为欧拉线定理.已知△ABC的外心为O，重心为G，垂心为H，M为BC中点，且AB=4，AC=2，则下列各式正确的有

( )

分析：此题是以数学文化为背景，借助平面几何性质，设置涉及平面向量的线性运算与数量积的综合应用问题，可以通过基底法来处理，也可以通过平面向量的坐标运算来解决.

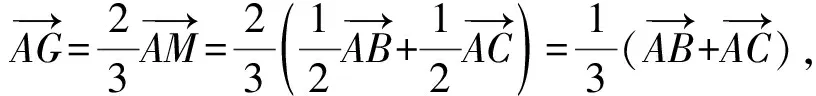
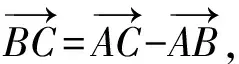
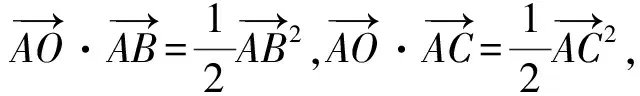
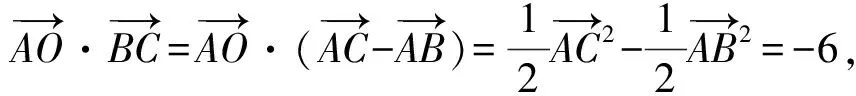
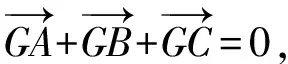
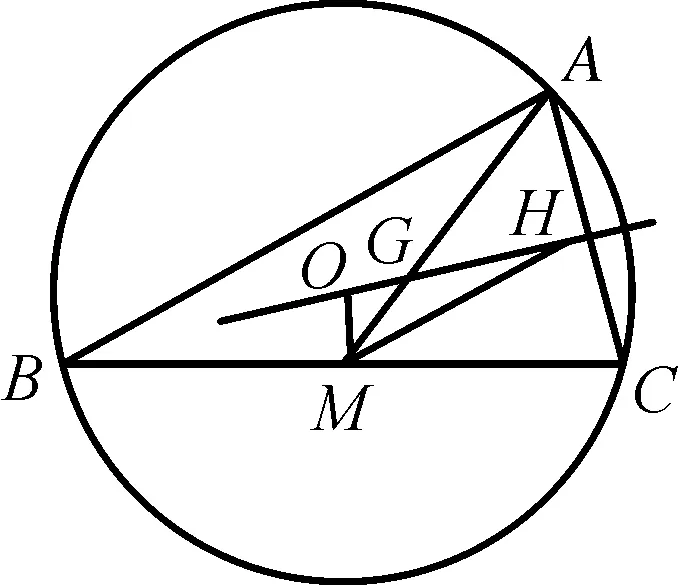
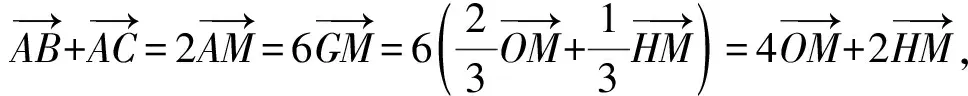
故选择答案：BCD.

点评：根据三角形的基本性质，结合三角形的外心、重心、垂心等特殊点构建平面向量关系式，利用平面向量的线性运算以及数量积运算加以转化，进而判断各选项的真假情况.基底法是平面向量中借助三角形法则和平行四边形法则的理解和掌握来解决问题的方法.

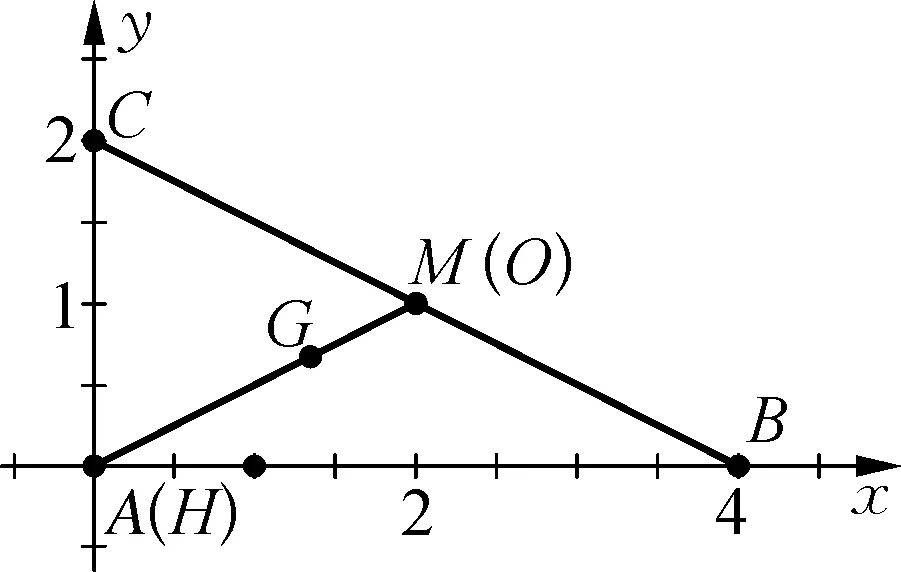
则点A与点H重合，点M与点O重合，

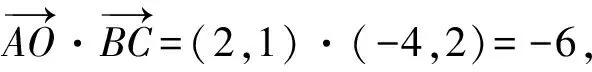
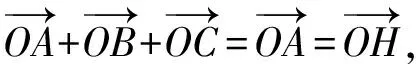
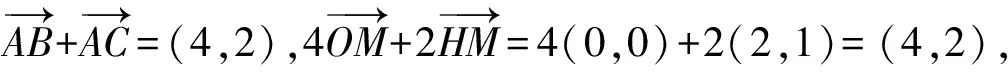
故选择答案：BCD.

点评：根据题目条件，利用特殊的直角三角形，构建平面直角坐标系，进而利用坐标运算与数量积公式等来分析与判断.通过坐标运算来特殊化处理的关键是需要根据题意，建立平面直角坐标系，从而实现问题的求解.

以三角形为问题场景来创设数学文化问题，融合初中与高中数学知识，借助知识之间的联系与过渡，引进数学文化情境，使得考生深刻认识到全世界各民族优秀传统文化的博大精深和源远流长.因而，在数学复习备考过程中，教师要有意识地加强对数学文化类试题的训练，进一步加强考生的应用意识，提升数学知识的应用能力，培养学生的探究与创新精神.