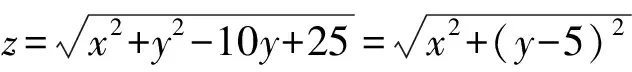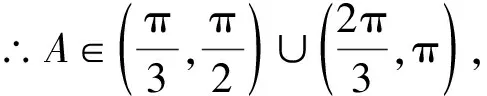数形结合思想在高中数学解题中的应用
贺启飞
(云南红河州第一中学,云南红河,661100)
数形结合思想是中学数学学习中常用的思想方法,特别在解决各类数学题目中发挥着重要的作用.
本文将详细介绍几种数形结合思想在解题中的应用,以便培养学生运用数形结合思想解题的能力.
1 通过函数图象实现对解答函数、方程、不等式问题的“数形结合”
对于函数、方程和不等式问题均是高中数学的常考题型.例如证明不等式成立、求解函数的值域和最值等问题,常以选择题和填空题,甚至是解答题的形式出现,综合性强且十分抽象.利用数形结合思想表示出各自对应的图象,再结合图象的性质进行综合分析,有助于快速解题,化抽象性为具体.总的来说,一般解答这类型问题的基本思路为根据题意表示出对应的图象,通过“以数解形”和“以形助数”分析所求问题即可.
例1若关于x的方程x2+2kx+3k=0的两根都在-1和3之间,求实数k的取值范围.
思考:本题需要利用等价转化思想,将关于x的方程转化为函数,分析这个函数图象与横坐标的交点个数,上述交点即为方程的解,通过分析在-1和3之间的两个根的情况求出k的取值.
解:令f(x)=x2+2kx+3k,图象如图所示:

图象与x轴的交点的横坐标等价于方程f(x)=0的解,
∵方程的两个根位于在-1和3之间,
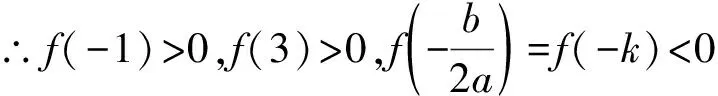
综上所述,实数k的取值范围为(-1,0).
变式训练1若方程lg(-x2+3x-m)=lg(3-x)在x∈(0,3)内有唯一解,求实数m的取值范围.

思考:一般来说,对于方程的解、函数的性质等进行讨论时,可以借助函数的图象直观解决,简单明了,根据方程只有一个解可得两个方程的图象只有一个公共点,依次作为解题突破口.
解:原方程可转化为-(x-2)2+1=m,此时x∈(0,3),
设y1=-(x-2)2+1,x∈(0,3),y2=m,
如图所示,在同一坐标系中表示出它的图象,
∵方程在x∈(0,3)内有唯一解,
∴y1与y2的图象只有一个公共点,
∴m的取值范围是-3 曲线与方程的对应关系多见于圆锥曲线问题中,考查学生对圆锥曲线和方程知识的综合运用,难度较大,通常在填空题和解答题中较为常见,需要同学们能够根据已知的数据或等式转化图象,根据图象和直线的交点个数求解.一般来说这类型问题的本质就是“以形助数”和“以数解形”的有机融合,通过代数式等表示出图象,以圆锥曲线的性质为依据进行解答. 思考:本题M这个集合很明显是圆在x轴上半部分的图象,而集合N就是一条斜率等于1的直线,将两个集合转化为相应的图象表示出来,则M∩N≠∅等价于半圆与直线存在公共点,求出其最值即可得到取值范围. ∴M表示以点(0,0)为圆心,半径为3的圆,且在x轴的上半部分, 而N表示斜率k=1,纵截距等于b的直线,如图所示, ∵M∩N≠∅, ∴直线y=x+b和半圆有公共点, 变式训练2求y=(cosθ-cosα+3)2+(sinθ-sinα-2)2的最值. 思考:本题就是典型的距离问题,可以将上述函数视为两个动点之间的距离,求其最远和最近时的大小即可,表示出其图象为两个圆,结合圆的相关知识可得两动点之间的距离的最值. 解:∵y=(cosθ-cosα+3)2+(sinθ-sinα-2)2, ∴等价于两个动点P(cosθ,sinθ)和Q(cosα-3,sinα+2), ∴这两个动点的轨迹方程分别为:x2+y2=1和(x+3)2+(y-2)2=1, ∴两条曲线上两点之间距离的最值即为所求函数的最值问题, 通过挖掘所给等式或代数的结构反应的几何意义表示图象,通过图象性质进行解题.解答这类型问题的关键是要根据所给的代数式挖掘出其中的几何意义,并能够根据相应的图象性质解题.对于这类型问题综合性很强,一般出现在填空题和解答题中. 根据图象可得:当∠A在第一象限且与圆相切时,OA的斜率有最大值, 此时OA与x轴的夹角等于60°, 解:令f(x)=x2+ax+2b=0, ∴这个二元一次不等式组的解是△ABC内的点(a,b)的集合, 不等式问题是高中数学中的重要题型,常见的题型,例如解决含参不等式问题,确定参数的范围,证明不等式成立等.解答这类型问题通过会涉及分类讨论,过程较为繁琐.将题设条件与几何图形相结合,运用数形结合思想就能理清解题思路,快速解答.而线性规划问题也是高中数学的常考内容之一,大多数以选择题的形式出现,占有的分值不高,属于基础题型,但这类型问题的求解也离不开数形结合.利用数形结合表示出相应的图象以后,分析相应的条件确定其取值范围,有助于减小题目难度,节约解题时间. 解:(1)作与x+2y=0平行的直线l, 当直线l经过点C时,z有最大值, 故zmax=3+2×5-4=9; ( ) 思考:本题涉及的函数是一个抽象函数,因此可以根据函数的相关性质求解,由题意构造一个符合条件的函数图象,根据图象性质和三角形内角范围求解. ∴f(x)的图象如图所示, 由图象可得:当f(cosA)<0时, 又∵A是△ABC的内角,∴A∈(0,π), 通过上述四种“数形结合”的应用可以知道,巧妙运用数形结合思想对解题能够起到事半功倍的效果.运用数形结合思想,不仅能够避免复杂的运算和推理过程,还能直观形象地发现解题技巧,得到解题思路,简化解题过程.2 通过曲线与方程的对应关系实现对问题的“数形结合”

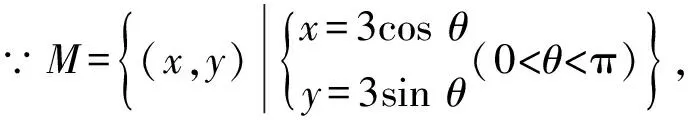
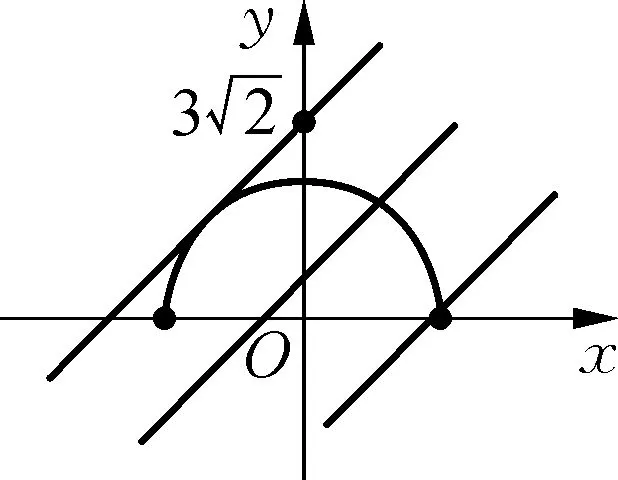

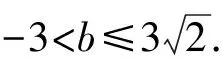
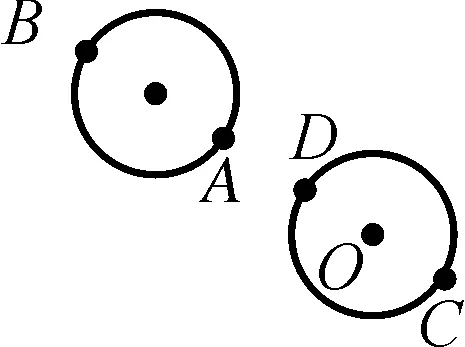

3 通过所给等式或代数式的结构的几何意义实现对问题的“数形结合”




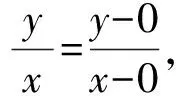

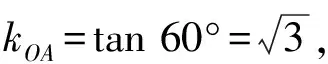




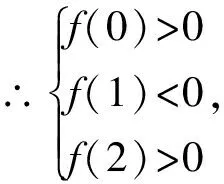
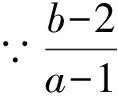

4 在不等式及线性规划中的应用.