问题驱动概念教学的实践与反思
——以“等差数列前n项和”为例
丁永刚 (江苏省徐州市第一中学 221140)
1 基本情况
1.1 授课对象
学生来自江苏省四星级高中重点班,数学基础较好,有一定的自学能力、逻辑推理能力和数学运算能力.
1.2 课标要求
《普通高中数学课程标准(2017年版)》(下称《课标2017》)指出:探索并掌握等差数列的前n项和公式,理解等差数列的通项公式与前n项和公式的关系;在数列教学过程中,可以组织学生阅读数列方面的研究成果,尤其是我国古代的优秀研究成果,感悟我国古代数学的辉煌成就.[1]
2 教学实践
2.1 细心观察,大胆猜想
问题1如何将下列古文“翻译”成现代文?
今有与人钱,初一人与一钱,次一人与二钱,次一人与三钱,以次与之,转多一钱,共有百人,问共与几钱?——《张邱建算经》
设计意图通过中国北魏时期《张邱建算经》中一道数学题导入所学内容,引导学生通过观察、讨论、“翻译”来发现问题中的等差数列,a1=1,a2=2,a3=3,…,a100=100,需求a1+a2+a3+…+a100.“翻译”的过程渗透数学建模方法解决实际问题的思想,借此引出本节课的第一个概念:等差数列{an}前n项和定义:一般地,我们称a1+a2+a3+…+an为等差数列{an}的前n项和,用Sn表示,即Sn=a1+a2+a3+…+an.回到古代的问题,转化为数学语言,提出问题2.
问题2如何求1+2+3+…+100?
学生活动 分组讨论首尾配对求和的原理和方法,讨论高斯求和的精髓和局限性.
设计意图适当渗透数学史,了解数学家 的故事.高斯求和的精髓在于首尾配对,体现了消项的思想,下面利用高斯求和法研究一个实际问题.
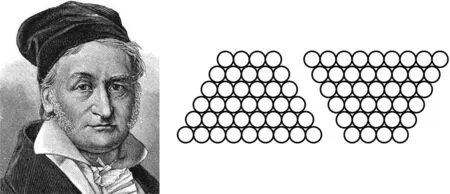
图1 高斯 图2
问题3怎样计算图2中钢管的总数?

问题4如何求1+2+3+…+n?
学生活动 小组讨论,如何求和?
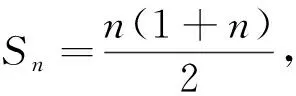
问题5猜想等差数列前n项和Sn=a1+a2+…+an的计算公式.
学生活动 思考并猜想结果能否与实际问题一致.
设计意图由问题4类比推理问题5,引发学生合理猜想,接着肯定学生的猜想,猜想出的结论需经过严格的证明,从而引出下一环节“合作探究,严格证明”.
2.2 合作探究,严格证明
问题6如何证明等差数列的前n项和公式?
学生活动 讨论一般情况下的等差数列如何推导求和公式,尝试总结公式的记忆方法.


问题7审视问题3解法中两幅图与解法的关系,能否避开分类,重新证明问题6?
设计意图为“倒序相加法”的出现做铺垫.

师:生2将数列中的每一项都用基本量首项a1、公差d表示,这是研究等差数列问题的通法,将数列通项的顺序颠倒后相加实现等差数列的求和.
问题8如何改进生2的证法,使之更简洁?
设计意图倒序相加已经呈现,但需要再次简化过程.

师:生3的证法更简洁直观,当数列首末两项的和a1+an为常数时,常用倒序相加法求数列的和,如何记忆此公式?
生4:借助梯形面积公式记忆更牢固.
设计意图小组讨论,学生多人合作终于完成证明过程,可以让学生感受倒序相加法的形成过程和使用条件,学生总结公式的记忆方法,完成知识建构.
2.3 新知初学,牛刀小试
问题9在等差数列{an}中,an=2n-1,求Sn.(结果用n表示)
学生活动 学生以抢答的方式进行,口述解题过程与结果.
设计意图让学生体会公式的简单运用,小试牛刀,提升学习的热情.
2.4 师生合作,公式运用
问题10等差数列{an}中:
(1)已知a1=3,a50=101,求S50;
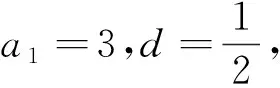
学生活动 学生回答解题思路与过程,教师黑板板演完整解题过程.


学生活动 学生在草稿纸上书写解题过程,教师利用投屏技术,展示学生完整解题过程,让学生讲解思路,鼓励学生一题多解.
设计意图本题是等差数列求和公式的逆向运用,训练学生逆向思维能力.
问题12已知等差数列{an},填写下表:

序号a1dnanSn112152-1327
学生活动 学生以小组为单位进行抢答.
设计意图此题是对于求和公式“知三求二”的巩固练习.
问题13在等差数列{an}中,已知第1项到第10项的和为310,第11项到第20项的和为910,求第21项到第30项的和.
学生活动 学生先独立完成,然后小组讨论,利用投屏技术展示完整解法.引导学生深入思考:此题除了基本量法之外,还有别的解法吗?
设计意图此题是公式的灵活运用,将题目条件化为基本量,这是解数列题的通法,强调通性通法.本题体现了化归转化思想,尊重学生思维发展的广度,鼓励创新解法.
2.5 课堂检测,巩固新知
问题14在等差数列{an}中,an=2n+3,Sn=an2+bn+c(a,b,c是常数),求a-b+c.
学生活动 通过抽签抽取学生答题,小组内部可提供帮助,10秒钟内若没有思路则重新进行抽签.
设计意图本环节为课堂检测环节,通过控件抽签器(利用Int函数,抽取随机数)抽取学生来答题,为求和公式性质的学习做铺垫,以此方式调动学生的学习兴趣,提高课堂学习的效率.问题9让学生初次体验计算成功的喜悦,问题10~12是公式的正用、逆用、变形用,层层推进,让学生感受数学解题中的变化.
2.6 小结提升,反思升华
问题15本节课你学到了哪些知识与技能、过程与方法?
3 教后反思
本课的授课对象整体水平较高,整个教学过程基本与课前预设一致,达到了预期的教学效果.
3.1 内容响应课标,突出重点
《课标2017》指出:在教学中可以组织学生收集、阅读数列方面的研究成果,特别是我国古代的优秀研究成果……感悟我国古代数学的辉煌成就.[1]本节课设计用到中国古代数学家张邱建的著作《张邱建算经》与高斯求和等数学文化内容,特别突出张邱建的研究,让学生体验深厚的民族自豪感.教学设计凸显数学建模、逻辑推理、数学运算等数学学科素养的培养指向,在教学目标达成的同时,传递给学生数学学习的必备品质、学习能力和正确的价值观念.
本节课的教学重点在于公式的推导,在问题3和问题4中让学生充分感受高斯首尾配对算法的局限性,通过教材上的实例,感受倒序相加法的巧妙之处,从而在公式推导过程中自然呈现.本节课的教学难点在于公式的运用,问题9到问题12均为对公式的运用.在问题10第(2)题中,将通项公式代入求和公式,可引出本节课的第二个求和公式,通过对两个公式与通项公式的分析,发现共有5个量,可“知三求二”.问题12为趣味竞答环节,设置控件抽签器,抽取学号,由学生现场抽题,激发了学生课堂学习的乐趣.
3.2 问题驱动探究,训练思维
数学是思维的科学,而问题是数学的心脏,语言是思维的外壳.布鲁纳说过:“教学过程是一种提出问题和解决问题持续不断的活动,思维永远是从问题开始.”本节课共设计了15个问题组成问题串(有预设的问题,也有生成的问题,如问题7和问题8),问题1让学生对等差数列前n项和的概念产生直觉猜想,问题2解决问题1提出的问题,问题3是问题2的特殊情况,问题4是从问题2、问题3的特殊情况到一般情况,问题5是问题4的更一般情况,问题6到问题8是对问题5的证明过程的层层改进,为引出“倒序相加求和法”做铺垫,由此获得对“倒序相加求和法”的本质的认识,可谓是精心设计.问题13和问题14是公式的灵活应用,体现了公式的应用价值,问题15有效地促进学生反思,在总结知识、升华内容的同时,有效培养了学生的理性思考和概括能力.15个高质量的问题驱动学生对等差数列前n项和的求和公式进行了深入的探究,由此获得对等差数列求和公式的本质认识,在问题串的驱动下,数学建构、数学探究过程严谨而又流畅,在潜移默化中训练了学生的思维能力.
3.3 过程引领发展,提升素养
学生经历“观察—猜想—证明—运用”的探究过程,探究等差数列前n项和公式的多种证明方法,通过古代数学问题发现了数列求和,继而提出如何求等差数列前n项和,通过小组合作,得出等差数列的前n项和公式.此过程中,学生发现问题、提出问题、分析问题、解决问题的能力得到培养,其从特殊到一般的逻辑推理能力得到训练,教师引领学生走上了科学研究的正确道路,提升了学生的学科核心素养.
3.4 知识表征多样,促进建构
20世纪80年代美国数学教育学家杜宾斯基提出了一种关于数学概念教学的APOS理论,该理论的主要观点是:学生学习数学概念就是心智结构建构的过程,具体可分为操作阶段、过程阶段、对象阶段和图式阶段.以此理论为出发点,本节课在设计教学流程时重视如何使学生在心智建构过程中发挥较好的主体作用.为此,笔者在设计教学过程时,向学生提供了图形、文字、符号等多样化的知识表征,创造出灵活变化的教学情境,激发学生的数学思考,给学生创造探索数学规律、发现数学本质的机会,使教学活动开展得富有成效,从而将探究式学习得到落实与推进[2].
3.5 知识鼓励应用,升华思想
在引导学生探索并证明等差数列前n项和公式之后,笔者还启发学生利用公式解决相关数学实际问题,体会和挖掘数学公式在解决实际问题中的作用.笔者一方面设计了配套的题组,使学生熟练掌握公式并加深对公式的理解;另一方面从形式上、结构上引导学生思考除了“知三求二”还有哪些应用与推广,随着后续章节的不断推进,学生会在后续学习中不断领会知识应用中渗透的相关数学思想[3].
——由倒序相加想到倒序相乘

