一种基于微波法珀谐振腔的高精度位移传感器

赵 刚， 马 畅， 张 琦， 陈 静， 向芸芸， 王一燚

(1.新疆阜康抽水蓄能有限公司，新疆 阜康 831500；2.上海大学 通信与信息工程学院 特种光纤与光接入网重点实验室，上海 200444)

0 引 言

精密制造业的迅速发展不断对精密测量技术有着更高的要求，位移传感器作为传感技术的一个重要分支，利用振动、厚度、形貌等几何参数发挥着重要的健康监测作用，如,在水电站监测中用来监测坝体裂缝[1]的宽度变化预防崩塌；在航天领域中，对零件有着极其苛刻的要求，一个较小的误差都会对整个航天器有着巨大的影响，检测航天器件零件的微小移动的变化十分必要。因此，制作一个稳定良好的位移传感器对工程不可缺少[2～4]。

工程中常用的位移传感器大多带有换算结构，例如差阻位移传感器[5]、振弦位移传感器[6,7]和光纤光栅位移传感器[8～10]，通过弹簧等元器件，将较大的位移转换成较小的应变，通过测量应变的大小来反推位移量，这些换算结构会降低传感器的精度；而直接对位移进行测量的原理，常用的有线性可变差动变压器(linear variable differential transfor-mer,LVDT)位移传感器[11,12]，LVDT的工作原理是将初级线圈产生的磁通量耦合到两个次级线圈，具有寿命长精度高等优点，缺点是量程很大时，线性度会降低；此外，还有非接触位移传感器，如激光测距仪等[13～15]，这类传感器含有芯片，在工程中使用会导致故障率上升。位移传感器同时面临着器件的稳定性和准确性的问题[2～4]。

为了解决上述问题，受光纤法布里—珀罗(Fabry-Perot)干涉原理[16,17]的启发，本文采用微波谐振原理[18]做出位移传感器。传感器由内导体、外导体和两个反射点构成，两个反射点之间的空腔为谐振腔。两个反射点的功能与光纤法布里—珀罗干涉原理类似，通过两个反射点分别反射回来的能量进行耦合，得到谐振频率。采用金属螺丝焊接内外导体，使内外导体短路，螺丝作为第一反射点。第二反射点与位移传感器的探杆固定为一体，位移变化带动第二反射器相对于第一反射器发生相对移动，使得微波谐振腔的腔长发生变化，从而影响频谱图中的谐振频率，也改变了谐振波长。通过测量频谱，可以发现谐振腔长的变化量与位移变化量呈线性关系。

1 传感器原理与设计

图1为微波传感器谐振腔部分的结构示意。微波传感器由外导体、内导体、第一反射点、第二反射点和谐振腔组成，所有部件的材料均为304不锈钢，谐振腔内的介质为空气。内外导体同轴，直径比值在1︰3～1︰2之间，第一反射点为不锈钢螺丝，焊接在内导体和外导体上，使得内外导体之间构成短路；内外导体的左端连接N转超小型A型(sub miniature A,SMA)射频接头，N转SMA射频接头的左端连接同轴电缆，信号通过同轴电缆传输到矢量网络分析仪(vector network analyzer,VNA)输出频谱；内外导体之间有一个可以移动的物体，该物体在第一反射点的右端且其左端面为第二反射点，第二反射点的移动使得两个反射点之间的距离发生变化。

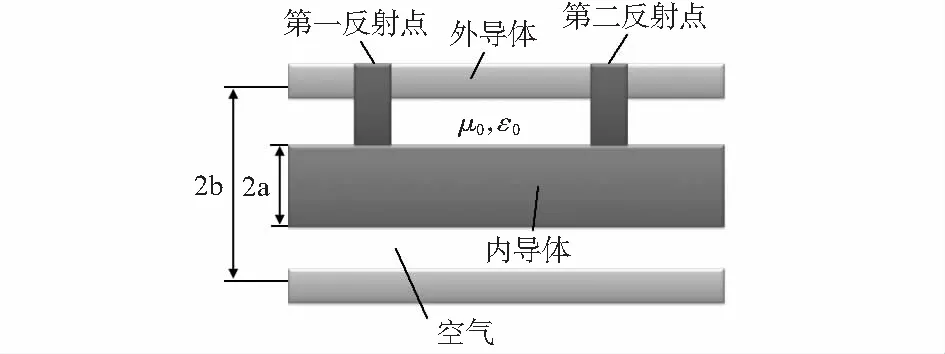
图1 微波谐振传感器示意

在传输线中，大部分电磁(EM)波被第一个反射点发生反射，其余的EM波穿过谐振腔到达第二个反射点。由于第二反射点是全断面遮盖的，所以到达第二反射点的EM信号在第二反射点发生全反射。由两个反射点反射的EM波在谐振器内部发生多次反射和干涉。两个反射波之间的相位延迟δ由下式给出

(1)

式中λ和f分别为EM波的波长和频率；d为谐振腔长度；εr为空腔内空气的相对介电常数；c为真空中的光速。对于谐振腔中的无限反射，反射系数可以表示为

(2)

式中r1和r2分别为第一反射点和第二反射点的反射系数，相当于空腔的损耗因子，它表示由空腔传输的入射波振幅的损耗。同时，在相位延迟(δ)等于2mπ(m为整数，即1,2,3，…)的频率处会有多个谐振频率。谐振频率fres和谐振波长λres的关系表示为

(3)

如图2所示，在位移传感器的设计过程中，传感器内外导体的左端连接有N转SMA射频接头，射频接头通过同轴线连接到矢量网络分析仪上，传感器的右端是标定位移传感器用的直线滑台，可以推动位移传感器的探杆，从而带动第二反射点发生移动。此时最重要的是如何设计结构使第二反射点移动过程中，位移可以连续且线性变化。这需要第二反射点与内外导体之间有良好的接触且接触点稳定。

图2 微波位移传感器和标定设备示意

如图3所示，第二反射点有2种设计方案，图3(a)为直接采用外径比外导体内径小0.05 mm、内径比内导体直径大0.05 mm的不锈钢刀刃状圆筒，这样与内外导体的接触宽度小于等于刀刃的宽度；图3(b)为采用带弹簧和顶珠的圆筒结构，圆筒的内径外径比外导体内径小0.1 mm、内径比内导体直径大0.1 mm，在圆筒靠近左端的地方有4个圆孔，2个孔口对着外导体、2个对着内导体，4个孔内均放有弹簧，弹簧上方有顶珠，顶珠在弹力作用下始终对内导体或外导体有一定的顶力，确保接触的良好性。

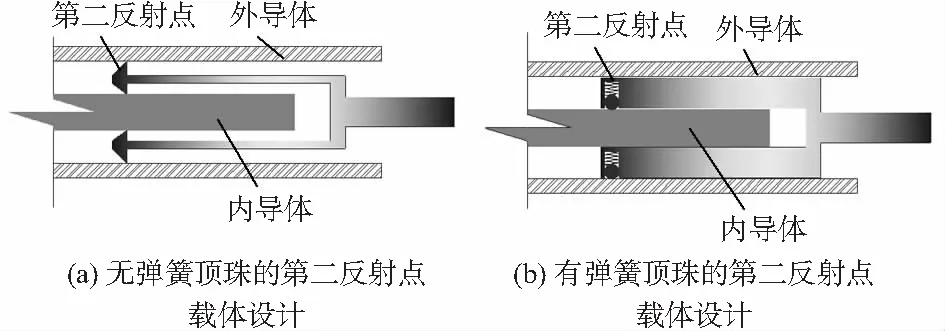
图3 2种第二反射点载体设计

为了验证哪种结构具有更好的接触性和数据连续性，这里进行缓慢移动测试，将位移传感器固定到缓慢移动滑台上，探杆顶在挡板上，滑台带动位移传感器发生移动，移动速度设置为30 μm /min (0.5 μm/s)。整个测试过程中，微波位移传感器测出的位移与时间的关系如图4所示。

图4 位移测量值和时间的关系

从图4(a)可以看出，图3(a)的结构测出的位移在一些测点存在跳数问题，跳动幅度最大可达0.5 mm，这是由于圆筒的刀刃与内外导体的接触点位置不稳定或接触不良造成的；从图4(b)可以看出，图3(b)的结构测出的位移连续性非常好，没有跳数，所以采用图3(b)的弹簧顶珠结构作为位移传感器的第二反射点。最后做出的位移传感器的实物如图5所示。

图5 微波位移传感器的实物

2 传感器测试

如图2所示，滑台和挡板固定在同一个光学平台上，传感器的主体固定在直线滑台上，探杆顶在挡板上，滑台带动传感器主体发生移动，使得第二反射点发生移动。用矢量网络分析仪作为信号源和检测器。从VNA端口输出的信号通过同轴电缆发射到传感器，接收位感器的反射谱。通过反射谱的谐振频率确定谐振波长，通过标定谐振波长与位移之间的关系，可以对位移传感器进行标定。

用直线滑台对位移传感器进行标定，一共标定往复3个测回，每个测回标定11个点，每10 %量程标定1个点。标定的典型频谱如图6所示。

图6 位移标定的频谱

6个频谱分别对应0,20 %,40 %,60 %,80 %和100 %量程。标定出3个测回的位移和谐振波长之间的关系如图7所示。可以得到，谐振波长λres与位移w的关系为λres=-1.928 7w+156.890，其中，w与λres的单位为mm。灵敏度(图7中的拟合斜率)定义为3个测回谐振波长平均偏移量与施加的位移的比例，该斜率-1.928 7，拟合度R2高达0.999。

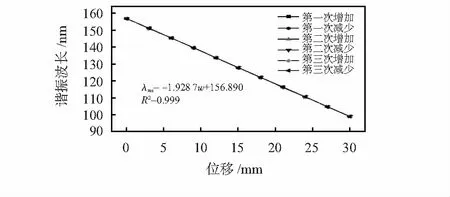
图7 3次测回，谐振波长与位移之间的关系

在温度标定中，将自由状态的位移传感器放置在恒温箱中。温度从0 ℃提高到50 ℃，每次升高5 ℃，共11个测点，标定出温度和谐振波长之间的关系如图8所示。位移变化量Δw与温度ΔT的关系为Δw=0.002 09T，Δw单位为mm，ΔT单位为℃。可见，由于材料热膨胀的影响，位移变化量随着温度的升高而增加，两者呈线性关系。

图8 位移变化量与温度之间的关系

对位移传感器进行稳定性测试，将位移传感器置于恒温箱内，温度设置为20 ℃，温度计的精度为±0.1 ℃。连续测量100次，位移波动量的测量结果如图9所示。可见，在温度不变的情况下，位移的最大波动范围为±1 μm。

图9 位移传感器的稳定性测试

3 结 论

本文提出并制作了一种基于微波谐振原理的高精度位移传感器。该传感器的两个反射点均为高反射点，第一反射点为固定点，通过移动第二反射点改变谐振腔长，从而改变了谐振波长和谐振频率，通过测量谐振波长变化量可直接确定位移大小，没有机械转换结构和换算问题。在量程30 mm的情况下，分辨率可达微米(μm)级，而且通过将弹簧和顶珠安装在第二反射点上的结构解决了位移传感器跳数的问题。在位移传感器标定测试过程中，基于谐振波长变化量比位移的高位移灵敏度λres/w=-1.928 7,且温度依赖性λres/T=-0.004 04 m/℃，还证实了传感器读数具有很好的稳定性，在温度和位移不变的情况下，位移的波动范围为±1 μm。这种高精度、温度影响小且性能稳定的传感器可用于各个工程领域的位移测量，在水电站的坝体缝隙测量等领域具有巨大潜力。