基于自适应UKF的移动机器人室内定位算法研究*

许 万, 朱 力, 张宇豪, 方德浩

(1.湖北工业大学 机械工程学院，湖北 武汉 430068；2.武汉理工大学 机电工程学院，湖北 武汉 430070)

0 引 言

移动机器人室内定位问题一直是移动机器人领域研究的重点和难点。传统的移动机器人室内定位方法主要有：惯导定位[1]、里程计定位[2]、磁导定位、视觉定位[3]以及激光雷达定位[4]等。然而，上述定位方法都存在一定的缺陷，难以直接应用于移动机器人室内定位。

近年来，为打破传统单一传感器系统在某些环境下的局限性，需运用多传感器融合的定位方法。目前，常用的多传感器融合定位算法主要有卡尔曼滤波(KF)，互补滤波和粒子滤波(PF)等[5～7]。与互补滤波和粒子滤波算法相比，卡尔曼滤波算法具有更高的实时性能、更小的计算量以及更好的滤波效果。但是卡尔曼滤波算法主要是对线性系统中的预测值和观测值进行融合，而实际中系统往往是非线性的。因此，基于无迹变换的无迹卡尔曼滤波(unsented Kalman filtering,UKF)算法[8～10]被提出，用来解决非线性系统下的位姿估计。然而在进行UKF时，系统噪声和观测噪声统计特性一般都是未知的，当实际噪声和先验噪声特性不同时，UKF算法的精度会急剧下降，甚至导致滤波器发散。

为解决此问题，王力等人[11]改进了样本点的采样方式，通过加入比例系数替代原有的固定值采样，提高了算法的滤波精度。杨菁华等人[12]提出了一种改进的UKF算法，以多异类传感器观测量扩展融合后的信息为新观测量，建立混合坐标系下的非线性测量方程，有效降低了目标的定位误差。Luo K等人[13]根据协方差匹配技术在线估计和调整系统和观测噪声的协方差矩阵，从而提高了滤波精度。虽然以上改进取得了一定的效果，但所考虑的系统大多是确定性系统。实际上，在复杂室内环境下，移动机器人定位受到外部环境影响、传感器测量误差等干扰具有随机性。通常，观测噪声的统计特性可以预先由传感器的物理特性测得，但是系统噪声的统计特性往往是未知和时变的。

针对以上问题，本文在UKF算法的基础上，对里程计、陀螺仪、激光雷达定位系统等传感器数据进行融合，根据激光雷达定位系统的误差统计特性，预先校准观测噪声的均值和协方差矩阵，并利用自适应噪声估计器在线估计未知系统噪声的统计特性，以实现移动机器人在复杂室内环境下的精准定位。

1 移动机器人定位系统建模

1.1 移动机器人运动学预测模型

如图1所示，为双轮差速移动机器人在全局坐标系X-O-Y中的示意，XL-OL-YL为以激光雷达为坐标原点的局部坐标系。其中，移动机器人的位姿由X=[xyθ]T表示，(x,y)为移动机器人在全局坐标系中的坐标，其测量值来源于里程计，θ为移动机器人与X轴正方向之间的夹角，其测量值来源于陀螺仪。移动机器人的系统输入控制量由u=[vω]T表示，其中，v，ω分别为移动机器人运动的线速度和角速度，为惯性测量单元通过积分获得的测量结果。

若移动机器人在系统输入控制作用下从t-1时刻的状态Xt-1=[xyθ]T运动至t时刻的状态Xt=[x′y′θ′]T，其计算公式可以表示如下

(1)

由于陀螺仪测量偏差以及轮子打滑导致的里程计航迹推算误差，因此移动机器人的预测模型可表示为

Xt=f(Xt-1)+εt

(2)

式中f(·)为运动学模型推导传递函数，Xt为t时刻的状态量,εt为系统噪声，εt～(0,Qt)，E(εt)=qt。

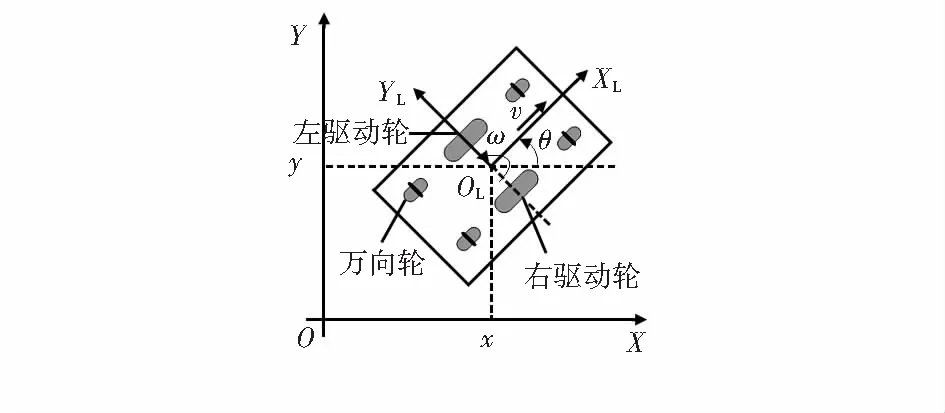
图1 双轮差速移动机器人运动学模型

1.2 激光雷达定位系统观测模型

在移动机器人多传感器融合定位算法中，通过激光雷达观测数据可实时校正里程计和陀螺仪等内部传感器的估算位姿，并消除累计误差的影响。

假设二维激光雷达对反光板的识别都是一致性匹配的，因此不存在错误的反光板匹配。根据基于最小二乘法的三边定位算法[14]，在t时刻移动机器人第i个反光板的测量值可以写为

(3)

由于激光雷达定位系统存在测量误差[15]，因此移动机器人的观测模型可表示为

Zt=h(Xt)+δt

(4)

式中h(·)为基于反光板的激光雷达观测函数，Zt为t时刻的观测量，δt为观测噪声，δt～(0,Rt),E(δt)=rt。

理论上，反光板的数量越多，激光雷达定位系统的精度越高。但是在实际应用场景下，激光雷达定位系统存在如下问题：1)移动机器人在复杂室内环境下运行的过程中，由于不确定性障碍物的影响，会出现部分反光板被遮挡的情况，从而导致定位偏差；2)激光雷达的更新频率一般为10 Hz左右，要远远低于算法的控制周期，这会导致在一个控制周期内传感器数据得不到实时更新。因此,在移动机器人室内定位中，需要融合其他传感器数据来进行位姿估计。

2 自适应UKF定位算法

2.1 UKF定位算法

本文采用UKF算法，对里程计、陀螺仪和激光雷达定位系统的定位数据进行融合。

对于移动机器人非线性系统

(5)

UKF定位算法的步骤为：

步骤1 初始化

(6)

步骤2 Sigma点采样

(7)

式中λ=α2(n+κ)-n，为尺度调节因子。α和κ为确定采样点的分布比例参数，取α=0.01，κ=3-n。β为非负权系数，取β=2最优。

步骤3 预测更新

(8)

(9)

(10)

(11)

(12)

(13)

(14)

步骤4 测量更新

(15)

(16)

(17)

(18)

(19)

由于系统噪声和观测噪声统计特性一般都是未知的，当实际噪声和先验噪声统计特性不同时，UKF算法的精度会急剧下降，甚至导致滤波器发散。因此,需要引入自适应噪声估计器对噪声统计特性进行估计和修正，以降低先验噪声特性不符合实际而产生的影响。

2.2 系统噪声自适应估计

在进行移动机器人位姿估计时，采用自适应噪声估计器对系统噪声的均值和协方差矩阵进行实时估计。同时，根据激光雷达定位系统的误差统计特性预先校准观测噪声的均值和协方差矩阵。

对于式(2)中的未知系统噪声，采用自适应噪声估计器对qt和Qt进行实时估计，得到系统噪声统计特性更新过程为

(20)

(21)

其中

(22)

式中b∈(0.95,0.99)，其目的为加大当前观测数据在历史估计中的作用。

自适应噪声估计器能够有效地跟踪系统噪声的统计特性，减小模型误差并抑制滤波发散，从而提高算法的鲁棒性和滤波精度。将系统噪声统计特性更新过程作为步骤5，对UKF算法中的系统噪声进行实时估计，即为自适应UKF定位算法的设计步骤。

3 实验验证

3.1 实验平台

本文所使用的实验平台为搭载激光雷达R2000的双轮差速车MIR100，主要包括3个部分：上位机、移动机器人底盘和激光雷达定位系统。实验环境为室内测试环境，在水平桌面上摆放半径为55 mm的圆柱形反光板，实验地面为平坦瓷砖地面。实验平台如图2所示。激光雷达定位系统通过局域网将定位数据传给移动机器人。

图2 实验平台

3.2 实验结果

为验证本文提出的自适应UKF定位算法的定位效果, 在系统噪声统计特性未知的情况下，将激光雷达定位系统的观测值和未加自适应噪声估计器的UKF定位算法作为对照组实验。实验中使用的反光板位置数据，如表1所示。

表1 反光板位置数据

设定自适应UKF定位算法的估计初始值为

P0=diag[1 1 1],r0=[0 0 0]T,q0=[0 0 0]T

R0=diag[0.013 1 0.010 5 0.042 6]

Q0=diag[0.001 0.001 0.011]

(23)

分别选择直线与曲线两种具有代表性的移动机器人运动轨迹进行实验，如图3所示。

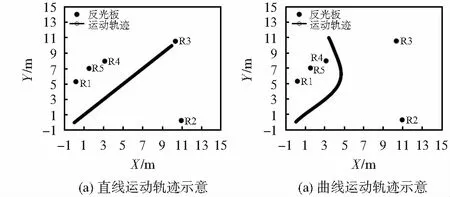
图3 移动机器人运动轨迹

移动机器人运动过程中，对移动机器人施加一次随机扰动，同时采集3种算法的定位数据，并计算其距离误差以及角度误差，绘制定位误差图，如图4所示。

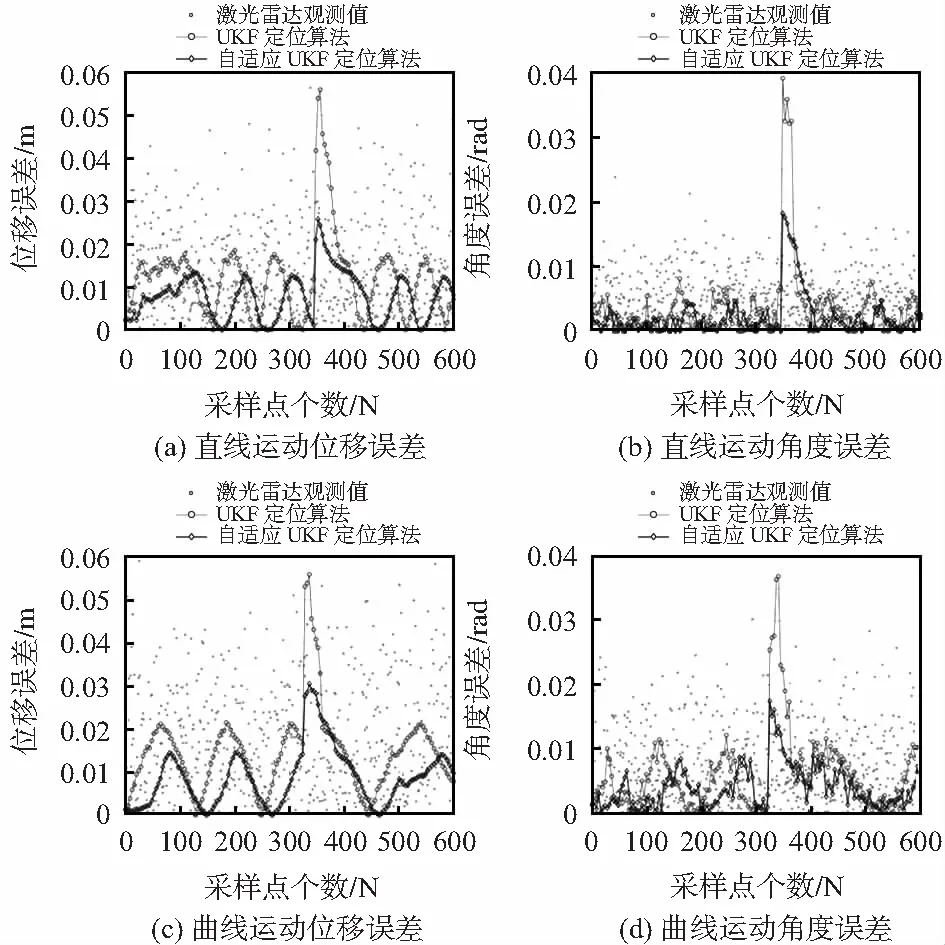
图4 移动机器人定位误差

根据距离误差和角度误差，计算出定位误差，如表2所示。

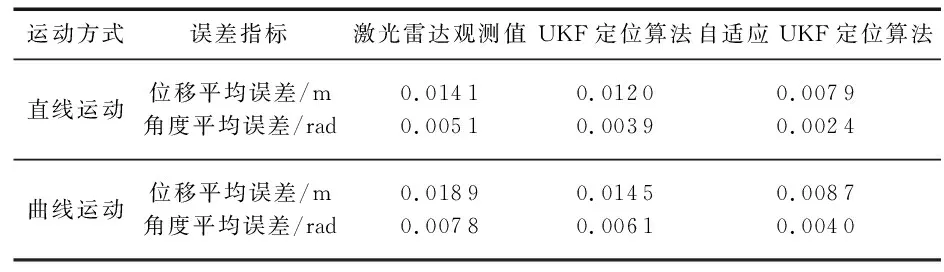
表2 各算法轨迹误差对比

由图4和表2可知，自适应UKF定位算法相比于UKF定位算法：在位置估计上，直线运动位移精度提高约34.2 %，曲线运动位移精度提高约40.0 %；在姿态估计上，直线运动角度精度提高约38.5 %，曲线运动角度精度提高约34.4 %。并且在随机扰动的影响下，自适应UKF定位算法比UKF定位算法的抗干扰能力更强。

4 结 论

在复杂的室内环境下，针对实际噪声和先验噪声统计特性不同而导致UKF算法精度急剧下降的问题，本文提出了一种自适应UKF定位算法。该方法首先以UKF算法为基础，融合里程计、陀螺仪、激光雷达定位系统等传感器数据，然后根据激光雷达定位系统的误差统计特性预先校准观测噪声的均值和协方差矩阵，并利用自适应噪声估计器在线估计未知系统噪声的统计特性，提高了滤波的数值稳定性，减小了状态估计误差。最后实验结果表明，相比于UKF定位算法，自适应UKF定位算法具有较强的鲁棒性和较高的定位精度，适用于复杂室内环境下的移动机器人位姿估计。