基于backstepping方法的两轮移动机器人轨迹跟踪控制

陈 滢，陈 炜*，杨贺贺，孙玉超，吴 航

（1.天津理工大学a.天津市先进机电系统设计与智能控制重点实验室，b.机电工程国家级实验教学示范中心，天津300384；2.天津理工大学中环信息学院，天津300380；

3.军事科学院 系统工程研究院卫勤保障技术研究所，天津300161）

移动机器人学是机器人学中的一个重要分支[1]。如今，移动机器人在军事、航海等领域能代替人类完成大量的危险任务，例如扫雷，海底勘测，无人驾驶，煤矿和地下工作等[2-5]。移动机器人也在人类的生产生活中发挥着重要的作用。在过去的20年中，由于理论和实际应用的需要，移动机器人的控制问题一直受到人们广泛关注。其控制问题一般可分为点镇定和轨迹跟踪问题。

随着科学水平不断提高，移动机器人轨迹跟踪问题受到越来越多研究者的关注。由于移动机器人是一种非完整约束的系统[6]，该系统不可积，所以移动机器人轨迹规划、镇定等问题较为复杂。近年来，轮式移动机器人已经在运动学控制方面进行了广泛的研究。例如，文献[7-10]首先对移动机器人的物理模型进行推导研究，并在机器人具有物理模型的基础下，根据不同控制方法对移动机器人的静态轨迹跟踪进行了大量的研究。

文献[11]中没有考虑移动机器人系统的非线性，特别是系统消除未知参数线性化的假设，忽略建模参数，使用模糊自适应神经网络研究控制，并直接在线研究系统模型。这对复杂机器人的研究具有深远的意义。但是由于移动机器人的特性，直接忽略机器人的非线性特性在实际操作中是不可取的。文献[12]提出了一种运用计算力矩法对移动机器人方程进行反馈线性化，并使用滑膜控制对移动机器人的运动轨迹进行跟踪。但是并没有对模型不确定性的移动机器人的动力学进行建模。

文献[13]设计了一种滑膜轨迹跟踪控制器，尽管该控制方法可以较好的处理模型不确定性及外部干扰，但是却存在抖振问题。文献[14]考虑到移动机器人运动的物理约束条件，提出了一种结合基于线性变分不等式的原对偶神经网络优化的模型预测控制方法来实现两轮驱动机器人的轨迹跟踪控制。但是该方法主要问题是计算量过大。文献[15]提出了一种与以往控制不同的控制器，一种以运动学和动态线性级联的形式提供类似反馈控制，是一种具有更简单和模块化的控制结构。由上述文献看出近年来对移动机器人控制的研究主要集中在运动学上。但是在大多数情况下，动力学问题不容忽视。本文的目的是分析和设计包括运动学和动力学在内的移动机器人的控制算法。

1 两轮移动机器人的建模

两轮移动机器人建模包括运动学建模和动力学建模。运动学建模解决了速度和位置之间的问题。动力学模型描述了速度与输入力之间的关系。两轮移动机器人的原理图如图1所示。点p是两轮移动机器人的中心，点G是两轮移动机器人的重要点。点p与点G重合。两轮移动机器人由全局坐标系中的向量表示。（x，y，θ）是移动平台转换的参考坐标。两个驱动轮的半径是r，两个轮子之间的距离是l。

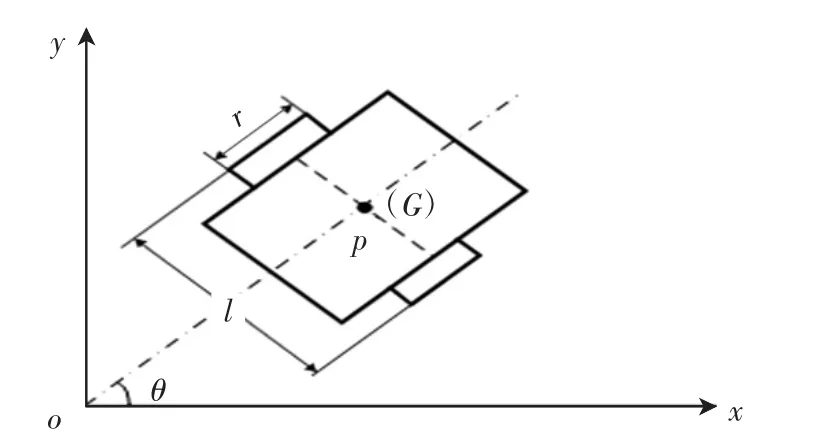
图1 移动轮式机器人原理图Fig.1 Structure of the two-wheel mobile robot

1.1 运动学建模

建立两轮移动机器人的运动学模型的目的是了解其运动状态。两轮移动机器人运动学模型如图1所示。

令p=（x，y，θ）T，q=（v，w）T，其中（x，y）为两轮移动机器人的位置坐标，θ为转向角，是两轮移动机器人行进方向和x正半轴的夹角，v和w分别为两轮移动机器人的速度和角速度。

假设两轮移动机器人在地面只做纯滚动运动，无打滑，则两轮移动机器人运动学模型[16]为

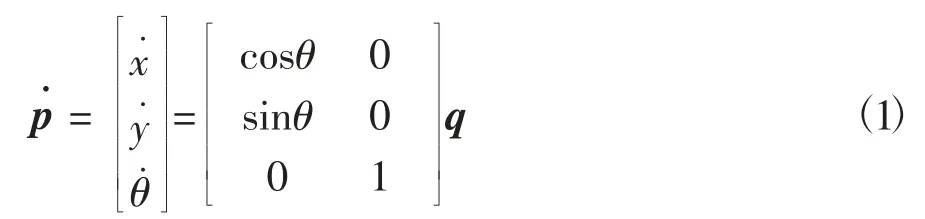
根据坐标变化，引入跟踪误差的概念，得到两轮移动机器人运动学误差方程

其中pe为理想位姿。

对两轮移动机器人的运动学控制，就是通过控制输入q=（v，w）T，来得到任意时刻的位姿误差。

1.2 动力学建模

假设两轮移动机器人在平面内移动[17]，设定全局坐标xoy为固定坐标系，则两轮移动机器人的动力学方程推导如下。

对于移动平台，由力矩平衡原理[18]，平台转动角度=动力转矩-阻力转矩，得

由牛顿第二定律，得

其中，IV是机器人重心的转动惯量；Fl和Fr是左右轮的驱动力；l为轮子到移动平台重心的距离；φ，v分别为移动平台的位姿角和线速度。

对于移动平台的车轮，根据力矩平衡原理，左右轮动态特性方程分别如下：IW为轮子的转动惯量，c为摩擦系数，k为驱动增益，u为驱动输入，θ、r分别指车轮转角和半径。

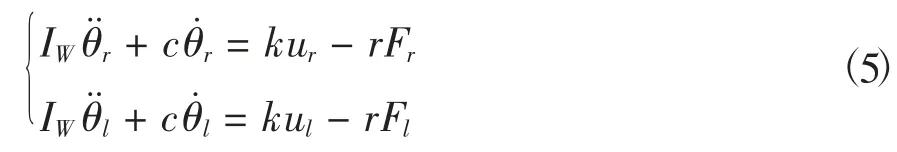
由两轮移动机器人运动学，得

由式（6）可得

由式（5）可得

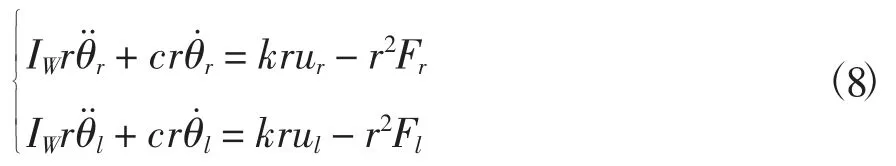
则

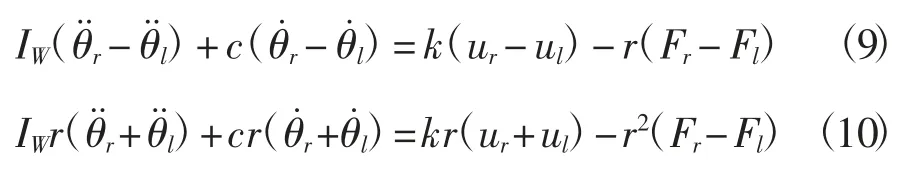
由式（7）可得

则

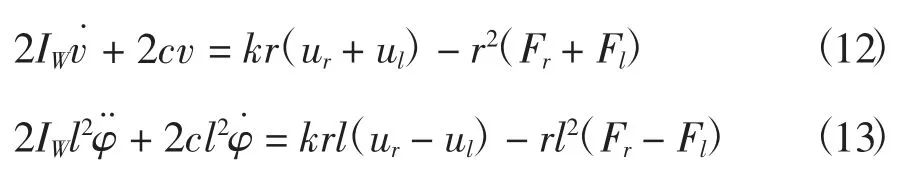
将上式分别代入（4）和（5），得

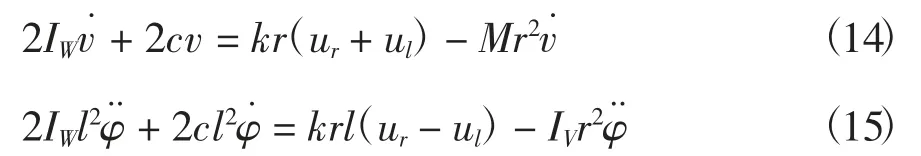
则可分别得到

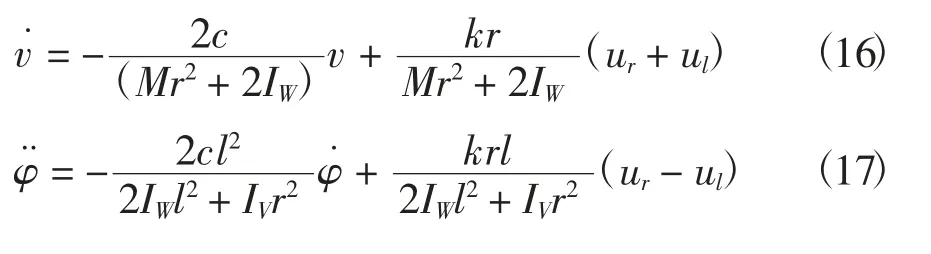
将式（16）和（17）写成两轮移动机器人动力学状态方程为

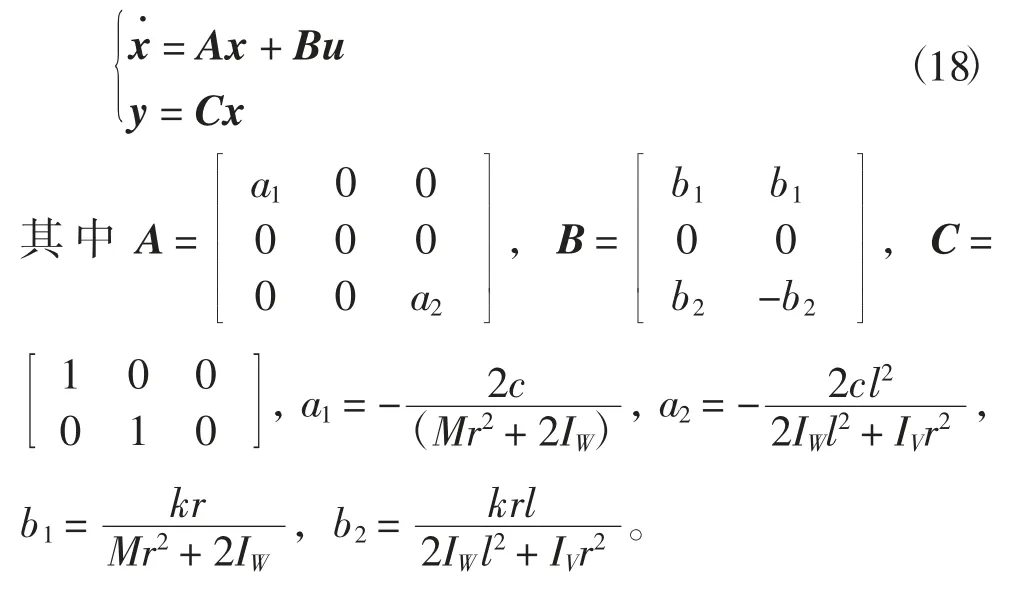
2 设计控制规律

本文采用backstepping控制分别对两轮移动机器人运动学和动力学进行控制设计。

2.1 运动学控制规律

考虑式（2）所示的运动学系统，设计轨迹为

其中xd，yd，θd表示移动机器人的理想位姿。

backstepping控制器的设计分为两步：

1）令虚拟输入α，根据式（2），取

令Lyapunov函数[19]为

由式（2）和式（19）式可得

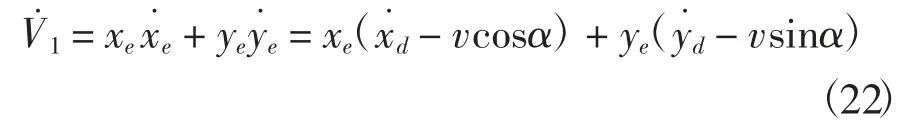
通过设计虚拟量α，使得

则

将线速度和虚控制律设计为

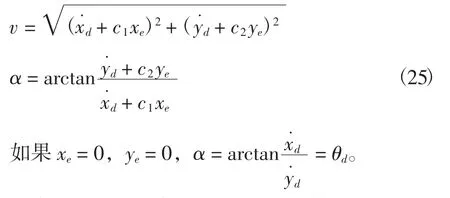
2）令e=α-θ，定义Lyapunov函数为

则

设计角速度控制律

则

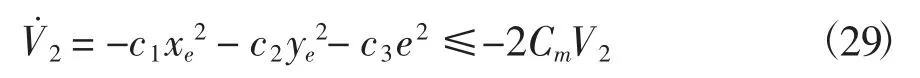
则t→∞时，xe→0，ye→0，θ→θd且以指数形式收敛。两轮移动机器人动力学控制器结构如图2所示。

图2 两轮移动机器人运动学控制结构Fig.2 The process of kinematics control

2.2 动力学控制规律

两轮移动机器人动力学状态方程（18）为线性方程。在设计动力学控制规律前，需要将式（18）进行线性解耦。

将式（29）代入式（27）可得到如下两个控制方程：

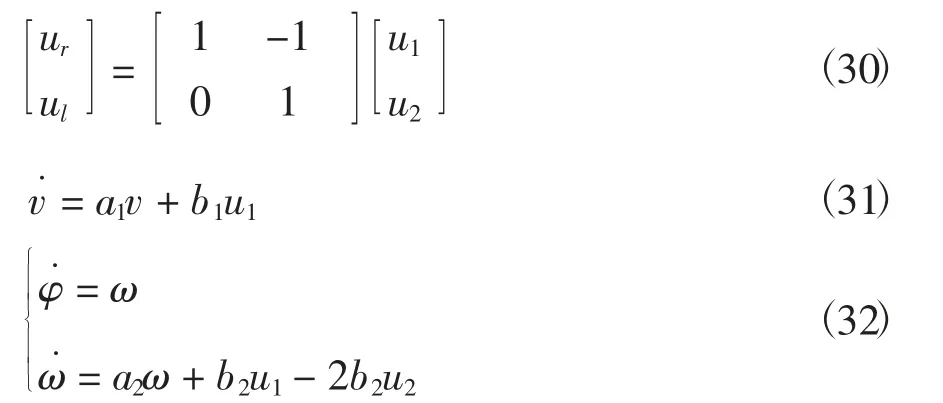
式（31）设计控制规律为：

假设理想速度为vd，速度误差为ve=vd-v。定义Lyapunov函数

则

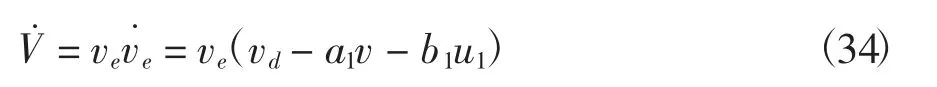
设计控制规律为

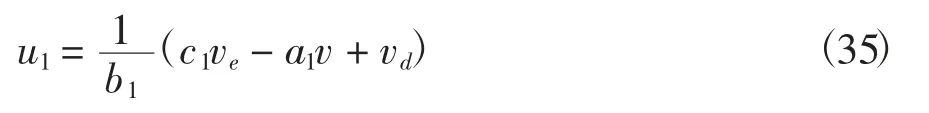
式（32）设计控制规律为：

假设理想角速度为φd，误差为z1=φ-φd，给定控制变量

其中c2＞0。

定义Lyapunov函数

则

定义Lyapunov函数

则

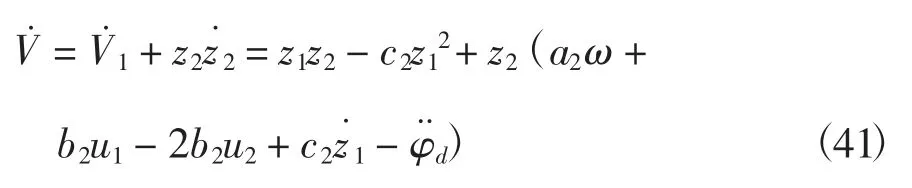
设计控制规律为

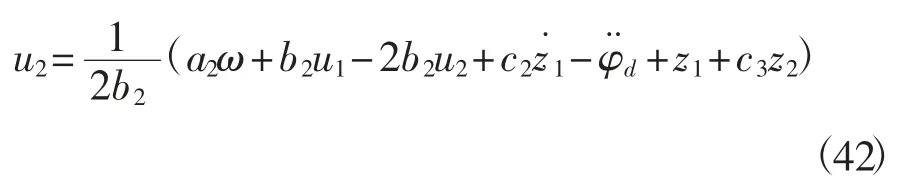
得到

则V（t）≤e-2CmtV（0），当且仅当t→∞时，φ˙→设计好的动力学控制器结构如图3所示。

图3 两轮移动机器人动力学控制结构Fig.3 The process of dynamics control

3 数值仿真

为验证控制规律设计的有效性，分别对两轮移动机器人运动学和动力学进行仿真，并且进行路径为圆形的轨迹跟踪。

3.1 运动学仿真

为验证该方法的有效性，给出两轮移动机器人的理想运动轨迹，跟踪移动机器人预设位置。设两轮移动机器人的初始位置为［1 1 0］，其中位姿为x=cost，y=sint。控制律为式（24）和（27）。控制参数设c1=c2=c3=10，仿真结果如图4～图8所示。

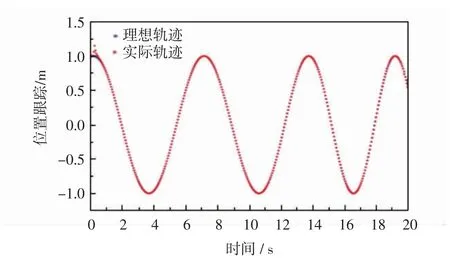
图4 x轴方向位置跟踪Fig.4 The trajectory in x axis

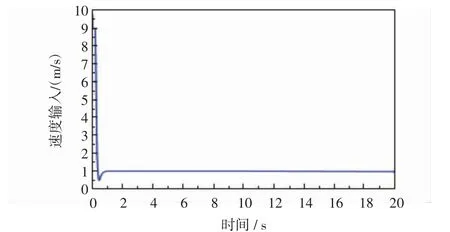
图6 速度控制输入Fig.6 The linear velocity input of the vehicle

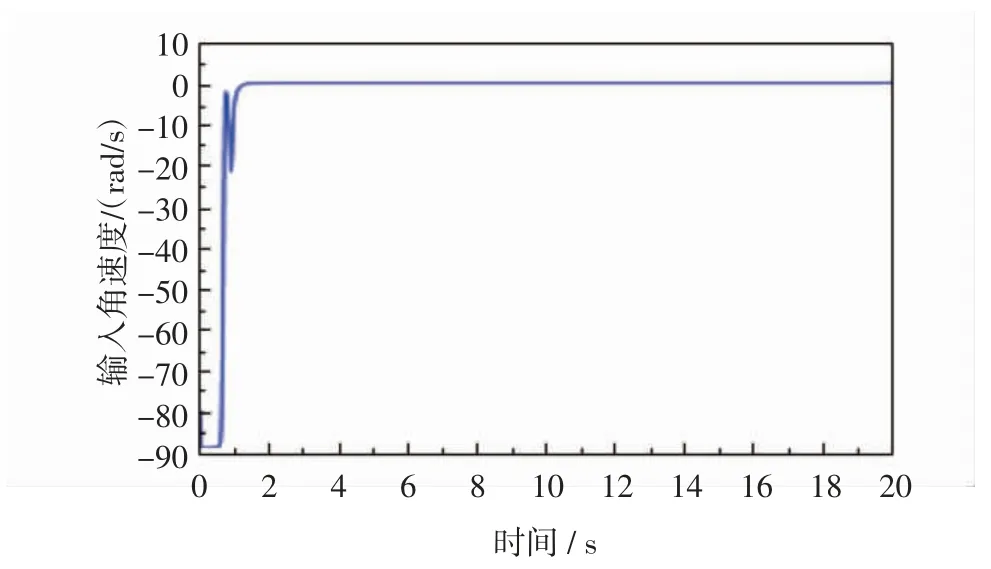
图7 角速度控制输入Fig.7 The angular velocity input of the vehicle

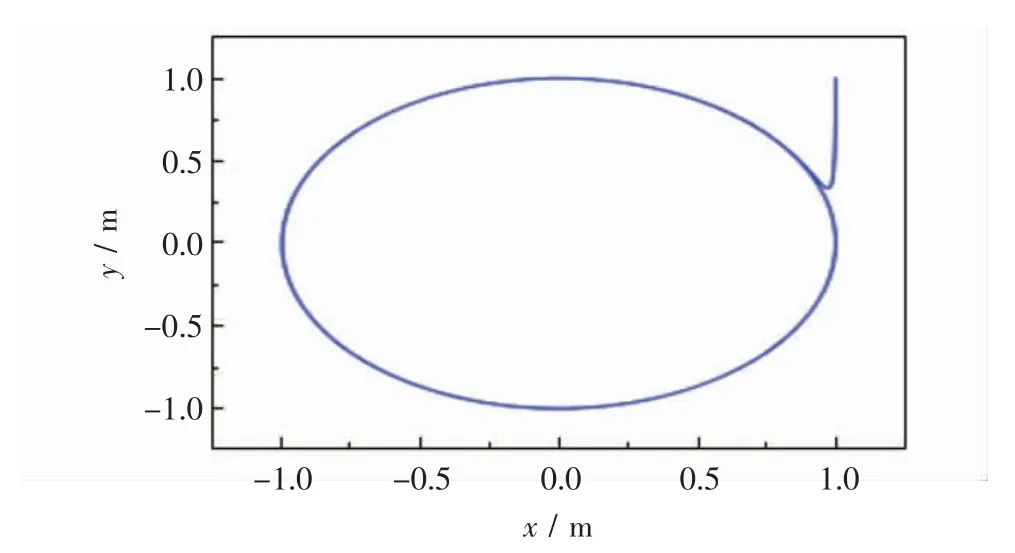
图8 位置轨迹跟踪Fig.8 The trajectory of the vehicle using kinematics control

从图4运动曲线看出，两轮移动机器人在x轴方向按照给定参考轨迹移动时，两轮移动机器人位置的瞬时值在初始状态下，与初始值偏差较大，在backstepping控制器的控制下，两轮移动机器人能够在0.50 s的时间内，能够迅速缩小和参考轨迹的误差。在0.5～20 s时间段内，实际轨迹和参考轨迹几乎重合。同理可得图5，两轮移动机器人在0.65 s后，实际轨迹与参考轨迹几乎重合。并且由图5看出，机器人运动轨迹平滑，无跳跃，说明该控制器在控制运动学有着良好的全局稳定性。

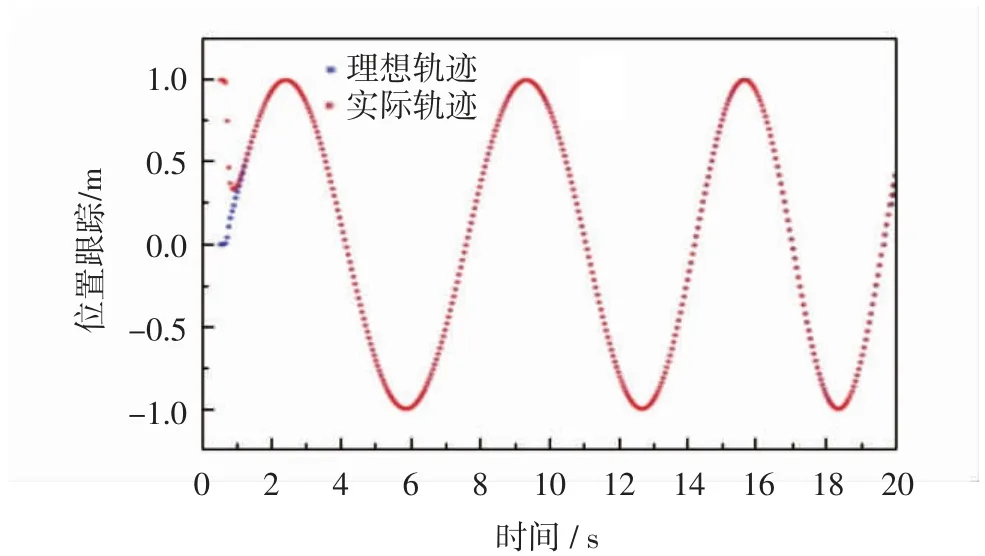
图5 y轴方向位置跟踪Fig.5 The trajectory in y axis

3.2 动力学仿真

为验证backstepping控制规律在两轮移动机器人动力学运动中的有效性，本文采用两轮移动机器人使用控制器前后的动力学进行比较。取线速度为vd=1.0，角度φd=-cost。采用式（34）、（41）作为动力学控制规律，取参数c1=c2=c3=10。

从仿真图9看出，未采用控制之前，两轮移动机器人实际转向角度与理想转向角度值相差较远。转矩曲线图10中，未采用控制器的两轮移动机器人左右轮转矩曲线波动明显。对比图11和图12，采用backstepping控制器后，两轮移动机器人的转动实际角度与期望角度在0～2 s有较大偏差，2 s后实际角度与理想角度曲线重合，成给定正弦曲线变化。采用控制器后的输出左右轮转矩曲线相较于未采用之前，曲线波动在1 s后逐渐趋于平稳光滑。

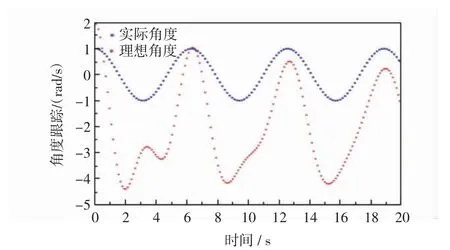
图9 未用backstepping控制器的两轮移动机器人的角度跟踪Fig.9 Angle tracking of the vehicle without backstepping controller

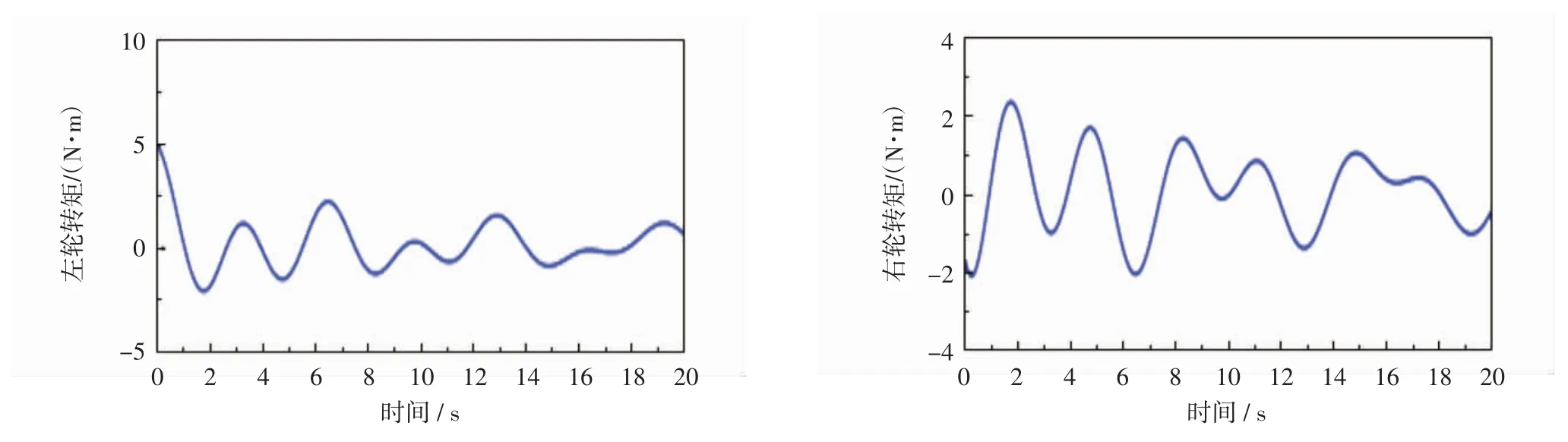
图10 未使用backstepping控制器时两轮移动机器人的转矩跟踪Fig.10 Torque tracking of the vehicle without backstepping controller

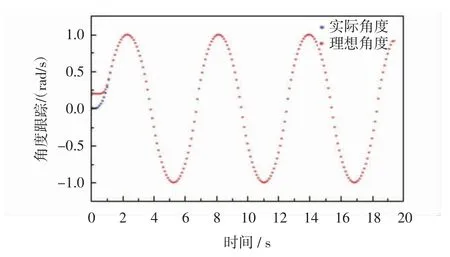
图11 基于backstepping方法的两轮移动机器人的角度跟踪Fig.11 Angle tracking of the vehicle based on backstepping controller

图12 基于backstepping控制器时两轮移动机器人的转矩跟踪Fig.12 Torque tracking of the vehicle based on backstepping controller

从仿真结果可以看出，本文所设计的控制律均能使各误差参数快速收敛于0。该控制规律有以下优点：引入虚拟量，采用backstepping控制器对运动学的线速度和角速度进行控制，对动力学的角度和转矩进行控制。如图8和图13所示，该控制器具有良好的稳定性和鲁棒性，采用Lyapunov函数提高了跟踪控制精度，实现了两轮移动机器人快速有效跟踪参考轨迹。

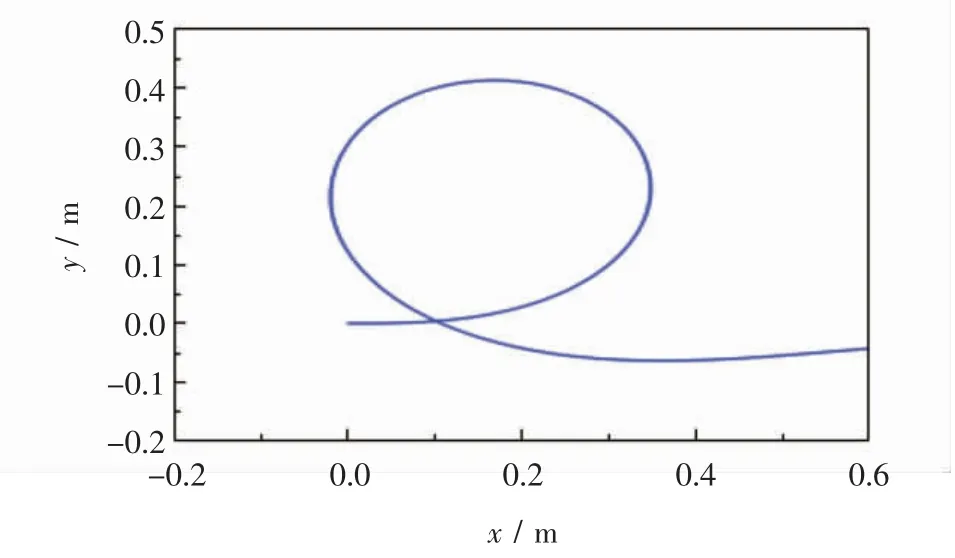
图13 位置轨迹跟踪Fig.13 The trajectory of the vehicle using dynamics control

4 结论

本文在两轮移动机器人的模型基础上，设计了backstepping控制算法对两轮移动机器人的运动轨迹进行了控制，通过仿真验证了该控制方法的准确性。首先对其运动学进行轨迹跟踪控制，针对两轮移动机器人的运动特性，对其轨迹跟踪进行了深入的研究。其次对其动力学进行控制算法的设计，使输入量位置和理论位置保持在一定范围内，使机器人运动轨迹有很好的平滑性。全文采用Lyapunov稳定定理保证了两轮移动机器人系统的全局渐进稳定性。